三相线钉扎的大液滴蒸发实验*
2022-04-13赵栋栋朱志强刘秋生秦军陶跃群
赵栋栋 朱志强 刘秋生 秦军 陶跃群
1(中国科学院力学研究所 微重力重点实验室 北京 100190)
2(中国科学院大学工程科学学院 北京 100049)
0 引言
液滴蒸发在DNA 微观序列的沉积[1]、直接喷墨打印[2,3]、透明导电薄膜制造[4]、喷剂干涸、液滴中颗粒物在固体表面的沉积、液滴式热交换的快速冷却、薄膜镀层[5]、定量表征材料吸湿性能[6]等工程应用中起着重要作用。同时,液滴蒸发涉及气液固三相间的相互作用,包含扩散、热毛细对流、浮力对流等多种作用机理,对热质输运耦合机理的理论发展具有重要科学意义。
液滴蒸发通常会经历三个阶段[7]:①接触半径R保持恒定,接触角θ逐渐减小的恒接触半径(Constant Contact Radius,CCR)阶段;②θ保持不变,R不断减小的恒接触角(Constant Contact Angle,CCA)阶段;③R和θ同时减小的混合阶段[8]。Birdi等[9]发现,小水滴在光滑玻璃表面(初始接触角θ0<90°)蒸发时处于CCR 模式,蒸发速率恒定且线性正比于R;而θ0>90°的水滴在Teflon 表面蒸发时处于CCA 模式,蒸发速率是非线性的。Rowan等[10]则发现,微水滴在PMMA 上的蒸发速率正比于液滴高度H而非接触半径R。Gelderblom等[11]发现,大接触角下瞬时蒸发速率会逐渐减小,而小接触角下瞬时蒸发速率几乎不变。
以往的研究侧重于特征尺度小于毛细长度的小液滴蒸发,此时重力效应的影响可忽略,气液界面在表面张力作用下呈球冠状,研究结果印证了Hu等[12]提出的准静态扩散蒸发模型。文献[13–15]发展了综合考虑扩散和自然对流的经验模型。
尽管小液滴蒸发规律已被大量研究,但对于特征尺度大于毛细长度且三相线处于钉扎状态的大液滴蒸发规律[13,16,17]仍需要开展深入研究。本文利用实践十号返回式科学实验卫星上的液滴蒸发实验系统,开展了R=5.7∼5.9 mm、初始体积V0=30.0∼120.0µL的无水乙醇大滴在加热PTFE表面的蒸发实验,对应Bond 数为12。一方面是为了探索三相线钉扎附壁大液滴的蒸发规律,另一方面也是作为实践十号空间附壁大液滴的地基科学匹配实验,通过与空间大液滴的科学数据对比分析,揭示重力对附壁大滴蒸发 的影响。
1 实验系统
图1 是实践十号附壁液滴蒸发实验系统,主要包含注液系统、光学观测系统、温度监测及控制系统以及环境监测与控制系统等。实验液体为无水乙醇,其物性参数列于表1。蒸发基座选择直径12.0 mm且厚度为100 µm 的PTFE 薄膜。PTFE 薄膜、铜台、直径10.0 mm 的热流量传感器与导热铝块之间通过3 M300 LSE 双面胶粘接。使用2 个热电偶反馈测量蒸发台面温度,由于PTFE 很薄且铜的导热性很好,忽略热电偶与基座表面间的热阻。通过PID 调节加热片功率使蒸发台到达预设温度Ts后,驱动电机推动活塞注出指定体积的液滴,记录CCD 相机拍摄到的液滴形貌图片。整个实验过程记录热流量变化、蒸发台面温度及环境压力。实验结束后,开启风扇清理环境中的蒸气并使基座降温。设定的液滴初始体积V0范围为30.0∼120.0 µL,实验过程中保持基座温度Ts=45.5±0.5℃,环境温度Ta=18.0±1.0℃。

图1 附壁液滴蒸发实验系统Fig.1 Experimental setup of sessile droplet evaporation

表1 无水乙醇物性参数(Ta=20.0℃,pa=0.101325 MPa)Table 1 Physical properties of ethanol (Ta=20.0℃,pa=0.101325 MPa)
2 结果与分析
2.1 液滴几何参量演化
不同液滴在蒸发过程中呈现恒接触角CCA、恒接触半径CCR 或CCA 与CCR 均出现的情况,如图2所示[8],本文研究的大液滴三相线处于钉扎状态,即图2(a)所示的CCR 阶段。

图2 液滴蒸发三个阶段Fig.2 Three stages during sessile droplet evaporation
液滴尺度大小与其受到重力效应或表面张力效应的影响紧密相关,衡量重力和表面张力相对大小的Bond 数以及毛细长度Lc的定义分别为
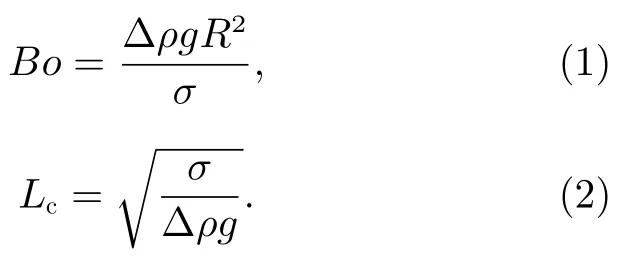
其中,ρ为密度,g为重力加速度,σ为表面张力。对于Bo<1即R
接触半径R可以反映加热基座上液滴的受热面积;接触角θ反映了液滴的润湿性能,其能够对某一时刻的液滴形貌进行定量表达,从而在液滴蒸发建模过程中得到广泛应用。利用自研的液滴形貌分析软件[18-20],对液滴蒸发过程中的体积V、接触半径R和接触角θ进行提取并使用初始值(V0,R0,θ0)进行归一化,结果如图3 所示。

图3 体积 V、接触半径 R、接触角θ 随时间的演化过程(V0=95.5µL)Fig.3 Droplet volume,contact radius and contact angle evolution when V0=95.5µL
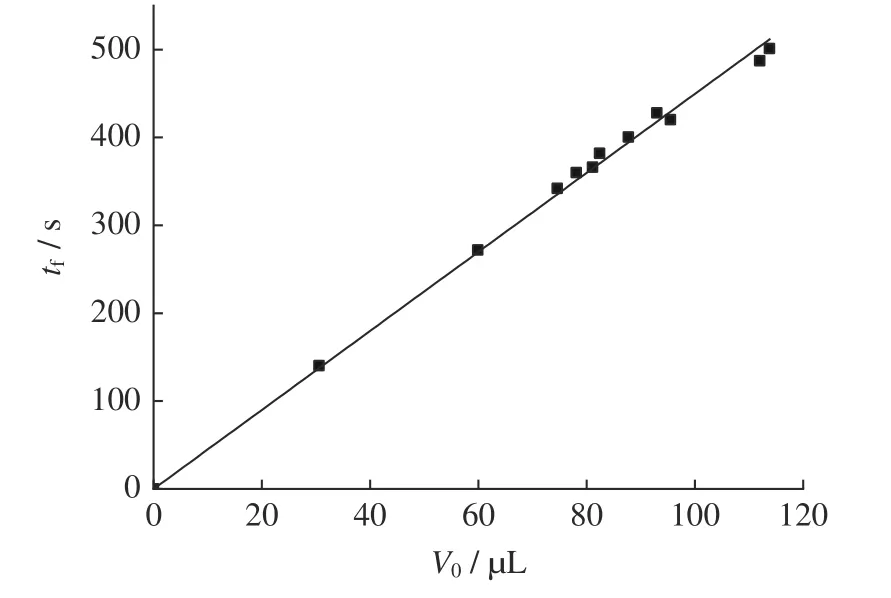
从V/V0=1到V/V0=0 所需时间定义为液滴的蒸干时间tf。对于在PTFE 表面的无钉扎无水乙醇小液滴(V0=5.0 µL,R0=1.8 mm)的蒸发[21],当t/tf=0.61时,R/R0=0.38;而在本实验中,当t/tf=0.85时,R/R0=0.96,表明本实验中液滴大部分蒸发时间内处于钉扎状态,未出现CCA 阶段。类似于R 对于一定体积的液滴,tf可以直观反映液滴蒸发的快慢:tf越小,液滴蒸发越快;tf越大,液滴蒸发越慢。tf大小与液体工质、基座表面材料、基座温度、环境温度等相关,此外其还与液滴的蒸发模式有关[21,22]。这里测量了不同初始体积V0下的tf,结果如图4 所示。由于液滴蒸发后期形成难以辨认的液膜,实验中对tf的获得通过体积V随时间t的变化外延来实现。 从图4 可以看到,拟合直线过原点,tf∝V0。每个初始体积V0下,V0/tf的值相等,这表明对于拥有相同接触半径R且三相线处于钉扎状态的大液滴,平均蒸发速率V0/tf与V0无关。三相线被钉扎时,V0的增大主要表现为气液界面面积的增大,同时三相线的形状及周长保持不变。但是气液界面面积的增大并没有显著加速蒸发,说明与小液滴的情况相同[12],受重力影响明显的大液滴的蒸发也主要发生在三相线附近区 域。 图4 三相线钉扎状态下不同体积(V0)的液滴蒸干时间tfFig.4 Dependence of tfon V0 when triple line is pinned (the straight line represents a linear fit) 在使用附壁液滴蒸发进行热管理的工程应用中,液滴瞬时蒸发速率的演化可以直接反映热管理的稳定性。无钉扎小液滴蒸发时,三相线会相继经历钉扎与去钉扎阶段,体积没有在整个蒸发过程中线性递减[23],即瞬时蒸发速率无法在整个蒸发过程中保持恒定。 Hu等[12]使用准静态扩散蒸发模型给出了瞬时蒸发速率的预测,即 式中,D为 扩散系数,csat为饱和蒸气浓度,计算由如下Clausius-Clapeyron 方程以及理想气体假设给出: 其中,psat、pref、Mv、L、、Tref、Ts分别代表饱和蒸气压、参考压强、蒸气相对分子质量、蒸发潜热、普适气体常数、参考温度和蒸发壁面温度。 Kelly-Zion等[13]发现准静态扩散模型会低估附壁大液滴的瞬时蒸发速率,在同时考虑蒸气扩散和空气中自然对流的情况下,提出如下经验公式: 其中,pa、ρ、g、Ma、υa分别代表环境压力、密度、重力加速度、空气平均相对分子质量、空气运动学粘度。 Carle等[14,15]只考虑扩散和蒸气对流,忽略热对流对瞬时蒸发速率的贡献,修正了Kelly-Zion等[13]的经验公式,有 将实验获得的钉扎大液滴瞬时蒸发速率与Hu 模型[12]、Kelly-Zion 和Carle 的经验模型[13-15]进行比较,结果如图5 所示。Hu 的准静态扩散模型初始时低估了实验瞬时蒸发速率约16%,且这一差异随时间的推移不断扩大,到0.85tf时,Hu 的预测低估了约29%。这是由于Hu 的准静态扩散模型忽略了浮力对流的贡献,而浮力对流有利于液滴内的能量输运,因而低估了基座传输到气液界面的热量,瞬时蒸发速率预测值偏小。 图5 瞬时蒸发速率的实验与理论结果对比Fig.5 Comparison of experiment and model prediction of instant evaporation rate evolution Kelly-Zion 模型预测值高于本实验测量值约15%,而Carle 模型预测值与本实验结果符合很好。这是由于经验模型中的拟合系数依赖于实验所使用的工质[15],Carle 使用与本实验相同的无水乙醇,Kelly-Zion 使用相对分子质量比无水乙醇要高的烷烃类工质,这种烷烃类工质在相同R下的浮力对流更加强烈,从而使得Kelly-Zion 模型预测值高于实验值。 实验中瞬时蒸发速率基本维持一个恒定值,而三个模型对瞬时蒸发速率的预测值均随着蒸发的进行而逐渐减小。Hu 模型对蒸发速率的预测与θ呈正相关,Kelly-Zion 和Carle 模型对蒸发速率的预测与R正相关,本实验中R的减小非常缓慢,因而Kelly-Zion 和Carle 模型预测值随着蒸发的进行变化很小。 实验中瞬时蒸发速率经历了短时间内迅速上升(当V0=113.8 µL时,这一阶段耗时约10 s)和之后的长时间内基本保持稳定两个阶段,而Carle 模型只预测了第二阶段的存在。基座底部注出的液体初始温度低于Ts,形成最大液滴时,基座提供热量的一部分需供给最后流入的液体升温,温度稳定后基座供热才基本上全部用于蒸发。因此瞬时蒸发速率开始时出现跃升,之后长时间基本保持稳定,这是无水乙醇滴在低热导率PTFE上蒸发时的一种非稳态效应[24]。由于PTFE 很薄,非稳态效应持续时间很短,因此瞬时蒸发速率的跃升十分迅速。文中三个模型均未考虑非 稳态效应,因此无法预测第一阶段的存在。 在重力环境下开展了一系列三相线处于钉扎状态的大体积附壁无水乙醇滴在等温PTFE 上的蒸发实验,主要结论如下。 (1)与小液滴蒸发的CCR 阶段相同,钉扎大液滴的体积随时间线性递减,蒸发过程中没有出现小液滴蒸发过程中的CCA 阶段。 (2)对于拥有相同接触半径且三相线处于钉扎状态的大液滴,平均蒸发速率与初始体积无关。与小液滴的情况相同,受重力影响明显的大液滴蒸发主要发生在三相线附近区域。 (3)准静态扩散模型低估了钉扎大液滴的瞬时蒸发速率,这是由于没有考虑自然对流的贡献。同时考虑蒸气扩散与空气中自然对流的经验模型的准确性依赖于实验所用工质。 (4)瞬时蒸发速率经历了短时间内迅速上升和之后的长时间稳定两个阶段。2.2 初始体积对蒸干时间的影响
2.3 瞬时蒸发速率演化



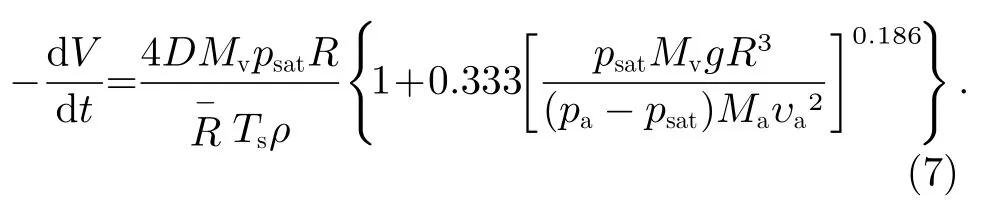

3 结论
