基于机器学习相似度算法的Kp 指数预报*

王子思禹 师立勤 刘四清 钟秋珍 陈艳红 闫晓辉 石育榕 何欣燃

1(中国科学院国家空间科学中心 北京 100190)

2(中国科学院大学 北京 100049)

3(中国科学院空间环境态势感知技术重点实验室 北京 100190)

0 引言

太阳风是太阳高层大气向外流动所形成的超声速等离子体流。当由日冕物质抛射事件或冕洞产生的太阳风到达地球时，会向磁层注入更多能量和粒子，可能引起磁层扰动，从而引发地磁暴[1]。地磁暴会严重影响卫星等飞行器的性能和安全，从而对整个空间和地面的技术系统的正常运行造成威胁。因此，对太阳风造成的地磁扰动进行及时预报具有重要的实际意义。

随着机器学习技术的不断突破，其自适应、自学习的强大并行信息处理能力，在很多方面取得了突破性进展。特别是在目标推荐系统中的应用：通过分析用户历史行为，提取特征并进行相似度计算，可以解决用户从大量信息中挑选目标信息这样复杂且耗时的问题[2]。同时，在空间环境监测方面，作为衡量近地空间全球磁扰强度的重要指标之一的地磁Kp指数，已有长达80年无间断的数据[3]；太阳风方面也积累了几十年的卫星监测数据。因此，将机器学习技术应用于空间环境监测信息处理，可以更有效地进行地磁扰动预报。

目前已有的机器学习地磁Kp指数预报模型有：Rice 大学Costello 模型[4]、Lund 天文台的Boberg 模型[5]、USAF WingKp模型（JHU/APL 模型）[6]、Rice大学的Bela 模型[7]等，但这些方法都属于基于人工神经网络的回归问题，需要较多的模型参数实现地磁Kp指数的预报。同时，预报员也因为受限于机器学习的“黑盒”过程，不能充分结合自身经验判断进行预报。本文通过机器学习的聚类算法和相似度算法，建立了太阳风推荐模型。利用该模型可以计算并推荐出与输入太阳风事例相似的多个历史太阳风事例。通过对模型推荐的太阳风事例的后续Kp指数进行分析，以及推荐太阳风事例与输入的太阳风事例参数变化的对照分析，预报员可以更加有效地将自身经验融入到地磁扰动的预报当中。同时，根据历史相似太阳风事例的后续影响，预报员可以更早地对当前太阳风事例后续变化做出判断和预报。

1 数据

太阳风及行星际数据来源于OMNI 网站*https://omniweb.gsfc.nasa.gov/。OMNI网站整合了来自IMP 8、Geotail、Wind 和 Ace 卫星的太阳风数据。本文选取ACE 卫星1998－2019年的太阳风数据，数据时频为60 s。考虑到卫星太阳风数据可能存在缺失，对于缺失数据首先进行数据清洗：将个别的缺省数据近似取值为其前60 s 对应的数据，保证了数据的完整性。OMNI 网站提供的太阳风参数包括太阳风速度v、太阳风质子密度N、太阳风温度T、GSM 坐标下行星际磁场By和Bz分量的值以及行星际磁场强度B。为了便于太阳风推荐模型的训练和学习，对太阳风参数数据均进行了归一化处理，消除不同量纲对计算的影响。

地磁Kp指数来源于OMNI 网站整合自德国地球科学研究中心（GFZ）的结果。根据机器学习模型输入要求，将Kp指数进行临近值预处理：即Kp指数30转化为3，3–转化为2.7，3+转化为3.3，以此类推。根据当前空间天气预报业务一般规范，把Kp指数介于5–和6+（包含5–和6+）定义为小磁暴，把Kp指数介于7–和90（包含7–和90）定义为大磁暴。

本文将世界时整点时刻后3 h 内的太阳风数据作为一个太阳风事例，进而将历史数据集划分成约18 万个太阳风事例，其中造成小磁暴影响的事例约4800 个，造成大磁暴影响的事例约450 个。另外，将时间上紧随其后的第一个Kp指数定义为与这一太阳风事例对应的Kp指数，太阳风事例领先其对应的Kp指数1～3 h，即预报时间提前量为1～3 h。

2 模型方法

太阳风是造成地磁暴的直接原因，因此具有一致性特征的太阳风引起的地磁扰动也应该具有相似的特征。在历史数据足够多的条件下，可以在历史数据中寻找到与当前太阳风特征相似的历史太阳风事例。历史太阳风事例引起的地磁变化，就可以作为当前Kp指数预报的参考。

本文主要利用机器学习中的相似度算法来构建寻找相似特征太阳风事例的推荐模型。具体的步骤分为3 步。第1 步，太阳风特征参数选取。可供选取的太阳风特征参数有速度、密度、温度、行星际磁场、行星际磁场By分量、行星际磁场Bz分量；在相似度计算中，过多的特征参数可能会导致推荐耗时倍增，且推荐结果会被无影响或极低影响的参数干扰，需要合理选取对地磁扰动起主要作用的参数作为相似度计算的特征参数。第2 步，参数权重计算。在地磁扰动中，太阳风各种特征参数的影响作用不同，需要对所选取的特征参数根据其对地磁扰动的影响计算相应的权重值。第3 步，推荐模型构建。本文以选定的太阳风特征参数作为输入，基于机器学习中的相似度算法，构建筛选相似太阳风事例的推荐模型。

2.1 太阳风特征参数选取

采用XGBoost 算法模型进行太阳风特征参数选取。XGBoost[8]是一个决策树训练模型，该模型依据输入的特征参数在迭代建立决策树中的作用和价值，即每个特征在所有树中作为划分属性的次数判断特征重要性，继而通过每个属性分割点改进性能度量的量来计算单个决策树的重要性，并由节点负责的观察数量加权，最终将一个属性在所有提升树中的结果进行加权求和后然后平均，得到重要性得分[9]。

以1998－2019年归一化后的太阳风速度v、太阳风质子密度N、太阳风温度T、行星际磁场强度B、行星际磁场By、Bz分量1 h 的平均值作为输入，以相应的Kp指数作为标签，通过XGBoost 模型迭代建立决策树，对输入的六个特征参数进行了评分。评分高低即为XGBoost 模型认为不同参数对地磁扰动（Kp指数）影响的重要程度。评分结果如表1。该结果也比较符合当前的研究结论，即磁暴的主相发展与行星际磁场的南向分量和正值行星际电场密切相关[10]。为了避免过多特征参数造成推荐结果的混乱，提高模型运行效率，经过随机的部分样本的测试，选择对地磁扰动影响最重要的两个参数：太阳风风速v和行星际磁场Bz分量作为太阳风事例推荐模型的输入参数时，推荐序列相似性和推荐耗时情况最好，所以本文最终选择v和Bz作为相似度计算输入的特征。

表1 XGBoost 对太阳风特征参数评分结果Table 1 Scores of feature parameters using XGBoost

2.2 参数权重计算

为了有效地计算筛选后的特征的权重，避免多余特征的影响，本文采用单层全连接神经网络对筛选后保留的太阳风风速v，行星际磁场Bz分量进行训练，并评估它们各自对地磁扰动影响的权重。以归一化后的太阳风风速v，行星际磁场Bz分量作为单层神经网络的输入层参数，时间分辨率是1 h，输出层为每小时相应的Kp指数，损失函数为预测值和实际值的均方差函数，优化器采用Adam（Adaptive moment estimation）算法[11]。通过单层全连接神经网络训练后，最终得到的权重比为|Wv|∶|WBz|=1.41∶1。

2.3 推荐模型构建

本文以机器学习中的相似度算法构建太阳风推荐模型，主要采用了欧氏距离和动态时间规整（Dynamic Time Warping，DTW）两种算法。欧式距离是指m维空间中两个点之间的真实距离，或者向量的自然长度，在二维和三维空间中的欧氏距离就是两点之间的实际距离[12]。设空间中两点X、Y的坐标为X(X1,X2,···,Xn),Y(Y1,Y2,···,Yn)，则X点与Y点间的欧式距离为

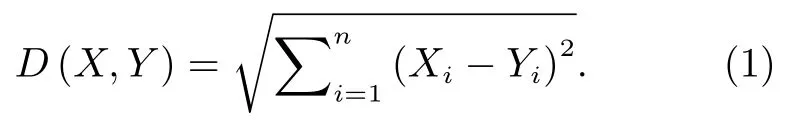
当其输入为两组特征参量时，可以反映两组特征参量之间的综合差异。

动态时间规整算法（Dynamic Time Warping，简称DTW 算法）是寻找时间序列相似的算法之一，其原理是给定两个序列Q={Q1,Q2,···,Qi,···,Qn}和C={C1,C2,···,Cj,···,Cm}，其长度分别是n和m，构造一个n×m的矩阵网格，如图1（a）所示，用红线和蓝线分别表示两个序列，以欧氏距离D为标准，矩阵元素(i,j)为Qi和Cj两个点的距离D(Qi,Cj)。从序列起始段所在的矩阵角为边界条件，在满足连续性和单调性约束的同时，通过动态规划求得距离累积值最小的路径即为最佳路径[13]。

如图1(b)所示，动态时间规整算法认为，通过对时间序列进行局部非线性缩放，使两个序列形态尽可能对齐后的欧氏距离累计值才是两个时间序列的最小距离。

图1 动态时间规整算法原理Fig.1 Principle of DTW

太阳风推荐模型包含初筛和精筛两个部分。初筛采用欧式距离方法，输入为一个太阳风事例中太阳风风速v与行星际磁场Bz的1 h 平均值，3 h 即为维度3×2 的矩阵。初筛通过逐个计算历史事例的3×2 矩阵与输入事例对应的3×2 矩阵的赋权欧式距离进行筛选，找到3 个距离最近的历史事例，作为推荐事例。精筛采用动态时间规整算法，输入为一个太阳风事例中太阳风风速v和行星际磁场Bz的60 s值，3 h 即为维度180×2 的矩阵。精筛计算历史上每个造成地磁暴的太阳风事例与输入事例之间的局部非线性缩放的欧氏距离，通过筛选找到最相似的3 个历史太阳风事例作为推荐的太阳风事例。太阳风推荐模型实际运行时，首先对输入事例进行初筛，若初筛结果为输入太阳风事例不会造成地磁暴，则不继续进行更高精度的推荐，仅选用初筛的结果作为预报参考。若初筛结果认为可能发生磁暴，则以每分钟时间间隔的特征参数作为输入，继续通过精筛在引发磁暴的历史太阳风事例中寻找相似事例，得到参数时间序列变化相似的历史太阳风事例作为模型精筛的推荐结果。空间天气业务预报中，一般对可能发生磁暴的情况更为关注，因此推荐模型的精筛主要针对磁暴事例。推荐模型中没有全部采用精筛方式，也考虑到在大量历史数据中进行动态时间规整算法计算时，用时可能较长，降低预报实时性。

太阳风事例领先其对应的Kp指数1～3 h，因此推荐模型的预报提前量为1～3 h。

3 模型测试结果

以1998－2019年的太阳风数据作为历史太阳风数据对推荐模型进行测试。测试中，从1998－2019年历史太阳风事例中随机选择120 个太阳风事例用作测试用例，这些测试事例覆盖了1998－2019年的全部年份，并且覆盖了从0～9 全部Kp指数的等级，其中没有造成地磁暴影响的、造成小磁暴影响的和造成大磁暴影响的比例为1∶1∶1，各40 个。

选取测试用例的最优推荐事例（非自身的top1）对应Kp指数与输入事例对应的实际Kp指数比较，测试结果如图2。图中横轴是输入太阳风事例对应的实际地磁Kp指数，纵轴是推荐的历史太阳风事例的地磁Kp指数；I 区是无磁暴影响的太阳风，II 区是造成小磁暴影响的太阳风，III 区是造成大磁暴影响的太阳风。由图可知，推荐太阳风事例的地磁Kp指数与输入太阳风事例的地磁Kp指数具有较好的一致性。Kp平均绝对误差为0.65，Kp指数推荐值与实际值的均方根误差为0.79，相关系数为0.93。

图2 推荐模型测试结果Fig.2 Test results of the recommanded model

表2 列出了典型的基于人工神经网络方法的已有Kp指数预报模型与本文模型的比较。对比结果表明，本文的推荐模型优化了参数输入量的选取，Kp预报结果的相关性更好，预报结果误差较小。

表2 本文模型与现有典型模型比较Table 2 Comparison between the model proposed in this paper and the existing typical models

本文模型可以推荐出3 个最相似的事例，测试中在3 个最相似的事例中总能找出较为理想的推荐结果（推荐事例与实际Kp的偏差在1 以内）。表3 给出了推荐的三个最相似的事例的距离与Kp平均绝对误差（保留两位小数）的统计结果。由表3 可知，尽管存在一些距离与Kp指数最小变化精度不同导致的例外，但距离越相近的事例，Kp指数预报值越可能接近实测值。

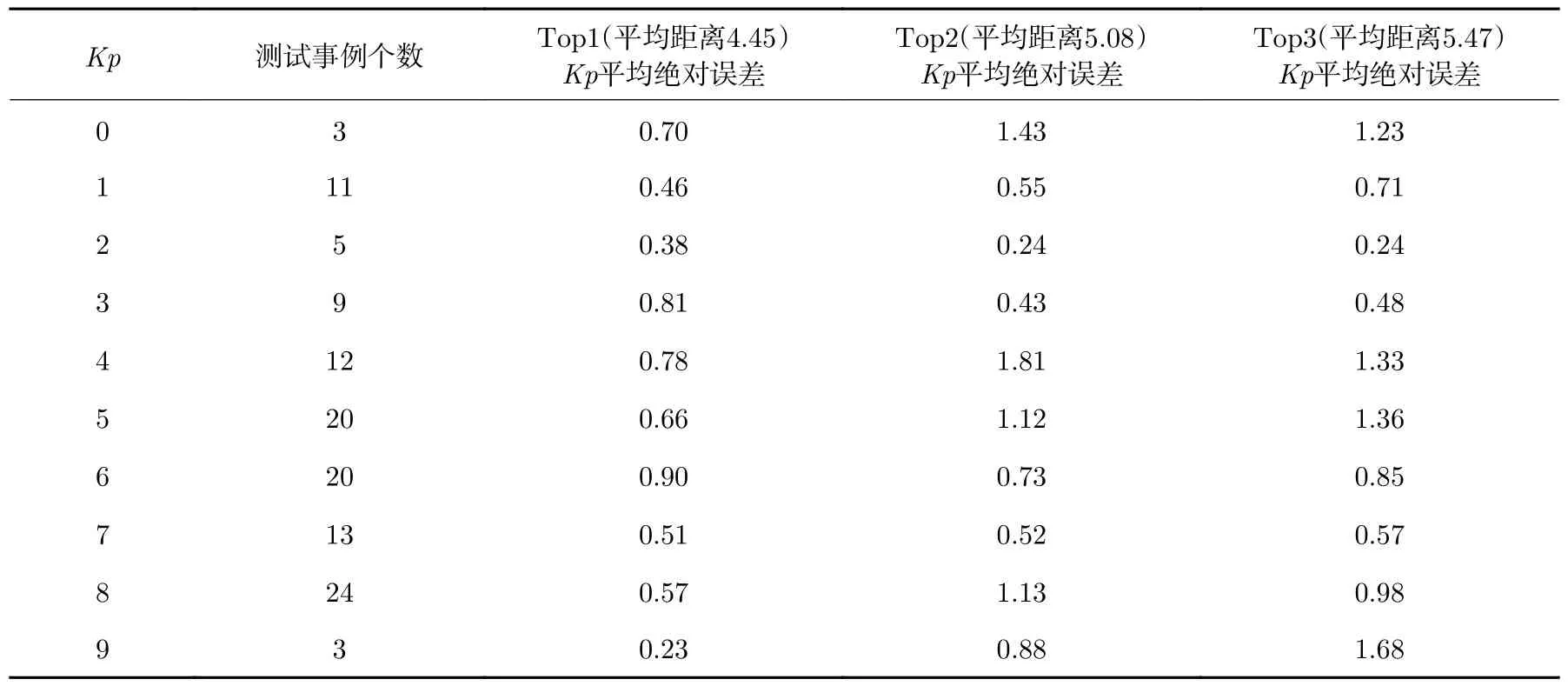
表3 不同Kp 指数下三个最相似事例的距离与平均Kp 误差Table 3 Distances of 3 recommanded cases and Kp error in different Kp indexes

4 讨论

由于太阳风对地球磁层的能量输入方式极其复杂且高度动态，进入地球磁层的能量可能快速耗散，也可能暂时储存在磁层内部缓慢地释放，所以现有各种模型很难给出精准预报。本文的推荐模型可以推荐出3 个最相似事例，预报员在实际应用中，可以直接采用最优推荐结果，也可以通过比对分析，优选其中之一作为预报参考。推荐结果不光可以为预报员提供直接的Kp指数预报值，还可以提供推荐事例与输入事例太阳风参数的时序变化对比，供预报员结合自身经验进行预报调整。

图3 中，红线表示2001年第90 天03:00 UT 的输入太阳风参数变化，绿线表示推荐事例之一的2003年第324 天11:00 UT 的太阳风参数变化，其中两张子图纵轴分别表示太阳风风速v和行星际磁场Bz分量，横轴均为太阳风事例的3 h 的时间序列。由图可知，输入的太阳风事例风速v更大，根据人工预报经验，当前输入的太阳风可能在地球磁层发生更多的磁重联，单位时间内的磁通量可能更大，因此输入到地球的能量可能更多，则对推荐事例的结果可以向上微调。而实际结果正印证了本文的推测，即实际输入的太阳风事例对应相邻的地磁Kp指数为9–，推荐的太阳风事例对应相邻的地磁Kp指数为8–。

图3 2001年第90 天03:00 UT 太阳风与2003年第324 天11:00 UT 太阳风参数变化的对比Fig.3 Comparison of solar wind parameters at 03:00 UT on the 90th day in 2001 and 11:00 UT on the 324th day in 2003

5 结论

本文以太阳风风速v和行星际磁场Bz作为输入特征参数，利用机器学习相似度算法计算输入事例的参数矩阵与历史事例的参数矩阵的距离，并根据距离排序结果进行推荐。与传统基于人工神经网络模型相比，本文的推荐模型基于XGBoost 算法剔除了其它特征参数对地磁Kp指数影响的非线性关系，直接通过相似的太阳风历史事例的地磁扰动影响指导当前太阳风的预报，测试结果表明该模型具有较好的地磁Kp指数预报效果。

本文的推荐模型避免了人工神经网络模型预报的“黑盒”问题。预报员可以通过该模型获取Kp预测值，也可以从多个推荐结果中看到输入太阳风事例与推荐的历史事例的参数变化对比,使预报员可以在预报中更多地结合自身预报经验，优选调整预报结果。由于太阳风与磁层相互作用的复杂性，推荐模型只是通过历史相似事件给出当前输入太阳风的可能影响，Kp指数预测精度的进一步提高也有赖于历史数据的积累。综上，本文的推荐模型可以为预报员提供一种更为实用的短时预报地磁暴的工具，也有利于预报员预报经验的提升。