Finite Time Blowup with Upper Bound of Blowup Time of Solutions to Semilinear Parabolic Equations with General Nonlinearity

(Col lege of Mathematics and Information,South China Agricultural University,Guangzhou 510642,China)

Abstract:In this paper,we consider a semilinear parabolic equation with a general nonlinearity.We establish a new finite time blow-up criterion and also derive the upper bound for the blow-up time.The results partially generalize some recent ones obtained by He Ma et al.

Keywords:Semilinear parabolic equation;General nonlinearity;Finite time blowup;Upper bound

§1.Introduction

In this paper,we consider the following initial boundary value problem of a semilinear parabolic equation with a general nonlinearity

whereΩ∈Rn(n≥1)is an open bounded domain with smooth boundary∂Ω,u0∈H10(Ω),T∈(0,+∞]is the maximal existence time of the solution,the nonlinearityf(u)in(1.1)satisfy the following conditions

In 1975,Payne and Sattinger[12]began to study the properties of solutions of equation(1.1)using potential well theory.Since then,potential well theory has been widely used and developed,and gradually became the main tool to study the properties of nonlinear equations.In[7],Levine first proved the nonexistence of global solutions for equations(1.1).In[1],Ball studied the finite time blowup problem and improved the result of nonexistence of global solutions for equations(1.1).Liu and Zhao in[10]considered the initial boundary value problem of problem(1.1)and semilinear hyperbolic equations.They investigated a threshold result of global existence and nonexistence of solutions,and also obtained the vacuum isolating of solutions.Finally they proved the global existence of solutions for problem(1.1)with initial conditionsI(u0)≥0,E(0)=dand 00,and they also showed that the solution blow up in finite time forJ(u0)0,the solution decays to zero exponentially ast→∞.Meanwhile,he obtained the solution blows up in finite time withJ(u0)≤d,I(u0)<0.Chen et al.[2]proved the global nonexistence of solution and asymptotic behavior of solution for problem(1.1).Gazzola and Weth[3]studied the initial boundary value problem of problem(1.1),wheref(u)=|u|p−1u.They proved finite time blow-up of solutions with high initial energyJ(u0)>dby the comparison principle and variational methods.Liu,Xu and Yu[9]discussed the Cauchy problem of problem(1.1),wheref(u)=|u|p−1u−u.By introducing a family of potential wells,they got the corresponding threshold results on the global existence,nonexistence and asymptotic behavior of solutions with initial energyJ(u0)≤d.Recently,Ma et al.[11]established sufficient conditions for finite time blowup with high initial energy and upper bound of corresponding blowup time on initial profile for the initial boundary value problem of equation(1.1)withf(u)=|u|p−1u.

Inspired by above works,we will show that the solution to problem(1.1)blow up in finite time for positive initial energy by using concavity argument[7,8]and negative initial energy by using the first order differential inequality method.Moreover,we also derive the upper bounds of the blowup time for both initial conditions.The results of this paper partially generalize some recent ones obtained by Ma et al.[11].

The main results of this paper are the following theorems.

Theorem 1.1.Let u(x,t)be the weak solution for problem(1.1)with u0∈H10(Ω)and f(s)satisfy(H).Assume that J(u0)<0,then the solution for problem(1.1)blows up in finite time.Moreover,we have the upper bound of the blowup time:

§2.Preliminaries

This proof is completed.

In this paper,the local existence of weak solutions to problem(1.1)can be obtained by Galerkins method,so the details are omitted.In order to state the main results precisely,the weak solution of problem(1.1)can be defined as follows:

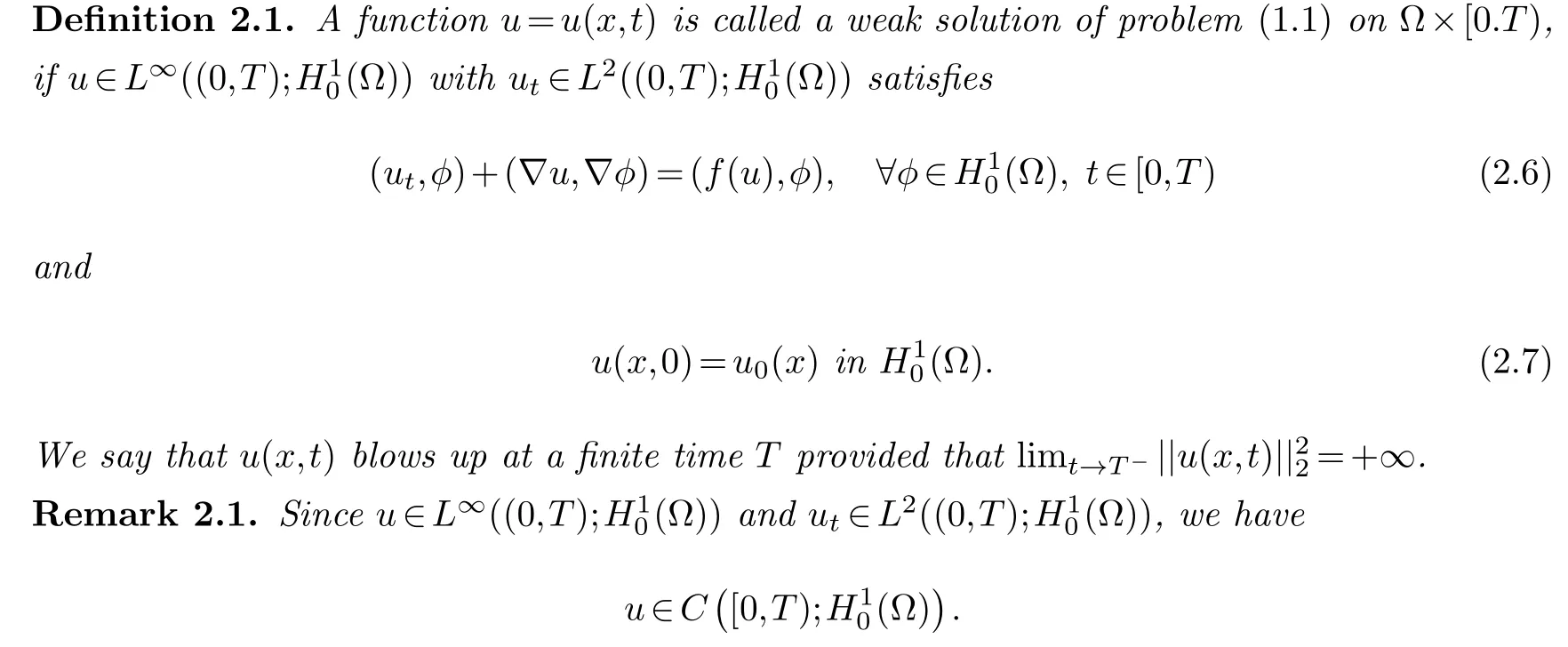
In order to estimate the upper bound of the blow-up time ofu(x,t)for thereom 1.2,we need the following basic lemma.

Lemma 2.2.[6]Assume for a positive,twice-differentiable functionψ(t)and some constant θ>0that there holds

§3.The proof of main results

Now,we give the proof of theorem 1.1 by applying the first order differential inequality method.

Proof of Theorem 1.1.Integrating(2.8)from 0 totrespect to time,then we have

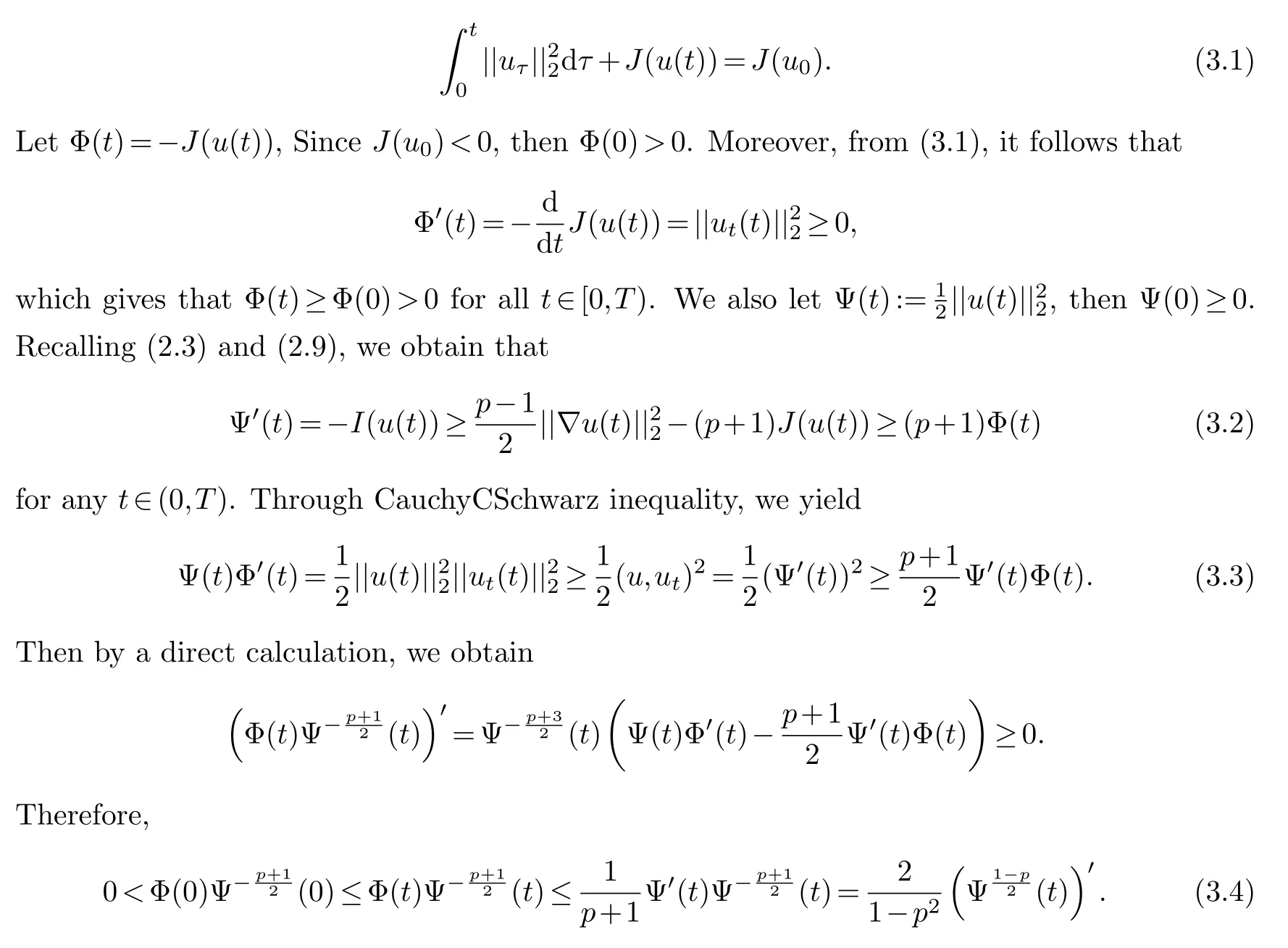
Now we prove high energy blowup and estimate the upper bound of the blowup time of the solution for problem(1.1).

Proof of Theorem 1.2.Here,we apply the concavity arguments to prove this theorem.The blow-up properties of solutions for other evolution problems are studied in a similar way[4,5,13,14].