Two Embedding Theorems in Martingale Spaces
2022-04-13
(School of Mathematics and Statistics,Henan University,Kaifeng 475004,China)
Abstract:It is proved in this paper that a pair of measurable functions satisfying the good−λinequality yields quasi-norm inequalities in Lorentz spaces and weak Orlicz-Lorentz spaces.By use of this conclusion two embedding theorems are obtained in martingale spaces.
Keywords:Good−λinequality;Martingale;Lorentz space;Weak Orlicz-Lorentz space
§1.Introduction
Lorentz space and Orlicz space are two important spaces that have been paid much attention to in recent years.The extension of the two spaces,Orlicz-Lorentz space,is a hot topic in functional analysis too.Among all of these spaces,the distribution function and the decreasing rearrangement functions are of good importance in both basic properties of the spaces and further research.Plenty of beautiful results have been obtained in these spaces and the weak case(see[1,7,8,12],etc.).Meanwhile the corresponding martingale spaces have been widely researched by scholars in atomic decomposition,weighted inequalities and interpolation(see[2,6,11,13],etc.).The good−λinequality can be seen in martingale spaces([10]).It is used to study the properties of Hardy martingale spaces.In([9]),Liu et al studied weak Orlicz martingale spaces by use of good−λinequalities to get the embedding relationships.Fan et al([3])established∗−good−λfor the rearrangement functions and obtained the relationships among classical Lorentz martingale spaces.In this paper,we will obtain some quasi-norm inequalities of measurable functions by use of good−λinequality and get two embedding theorems in martingale spaces.
Let(X,Σ,µ)be aσ-finite measure space andM(X)be the space of all measurable functions inX.Forf∈M(X),define its distribution function

and decreasing rearrangement

wherecwis a constant depends only onw.

§2.Main theorems and proofs
We say that an order pair of measurable functions(f,g)satisfies the good−λinequality,if for someα>1 and sequenceβn>0,there existsεαβn→0 and bounded sequencedαβn,such that
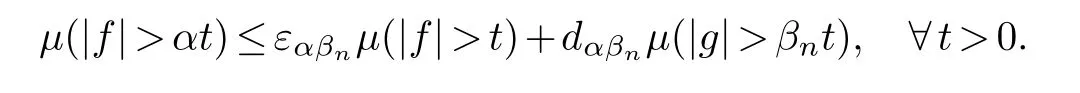
Now we prove the quasi-norm inequality forf,ginΛp,q(w)when the corresponding good−λinequality holds.
Lemma 2.1.Suppose0 Proof.First we consider the case when 0 SinceW∈Δ2anddαβnis bounded,there exists a constantcd,such that Proof.We need only prove for some constantC≥1 when‖g‖Λφ,∞(w)=1.Thus from the convexity ofφand definition of‖·‖Λφ,∞(w),we can get the desired inequality. In fact,in view of the good−λinequality of(f,g),we get which implies that This lemma is proved. Remark 2.1.It is easy to see that,given the constants in good−λinequality and the functions φand w,the constant C in the two lemmas are independent of f and g.So we can apply thisconclusion to sequences of order pairs. Now we turn to the embedding relationships between martingale spaces by use of the two lemmas.Let(Ω,Σ,P)be a complete probability space,and{Σn}n≥0a nondecreasing sequence of sub-σ-algebras ofΣwithΣ=σ(∪n≥0Σn). Define the maximal function,mean-square function and conditional mean-square function as follows: if{Σn}n≥0is regular. Now we will consider the similar results forΛp,q(w)andΛφ,∞(w). From[9]we know that(M f,s(f)),(S(f),s(f))and(s(f),S(f))(when{Σn}n≥0is regular)satisfy the good−λinequality.Combining with Lemma 2.1,we get the following theorem for martingales. Theorem 2.2.Let0 when{Σn}n≥0is regular. Proof.This is an immediate conclusion from Lemma 2.2 and good−λinequalities.Therefore we get the embedding relationships of the weak Orlicz-Lorentz martingale spaces.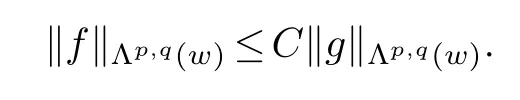

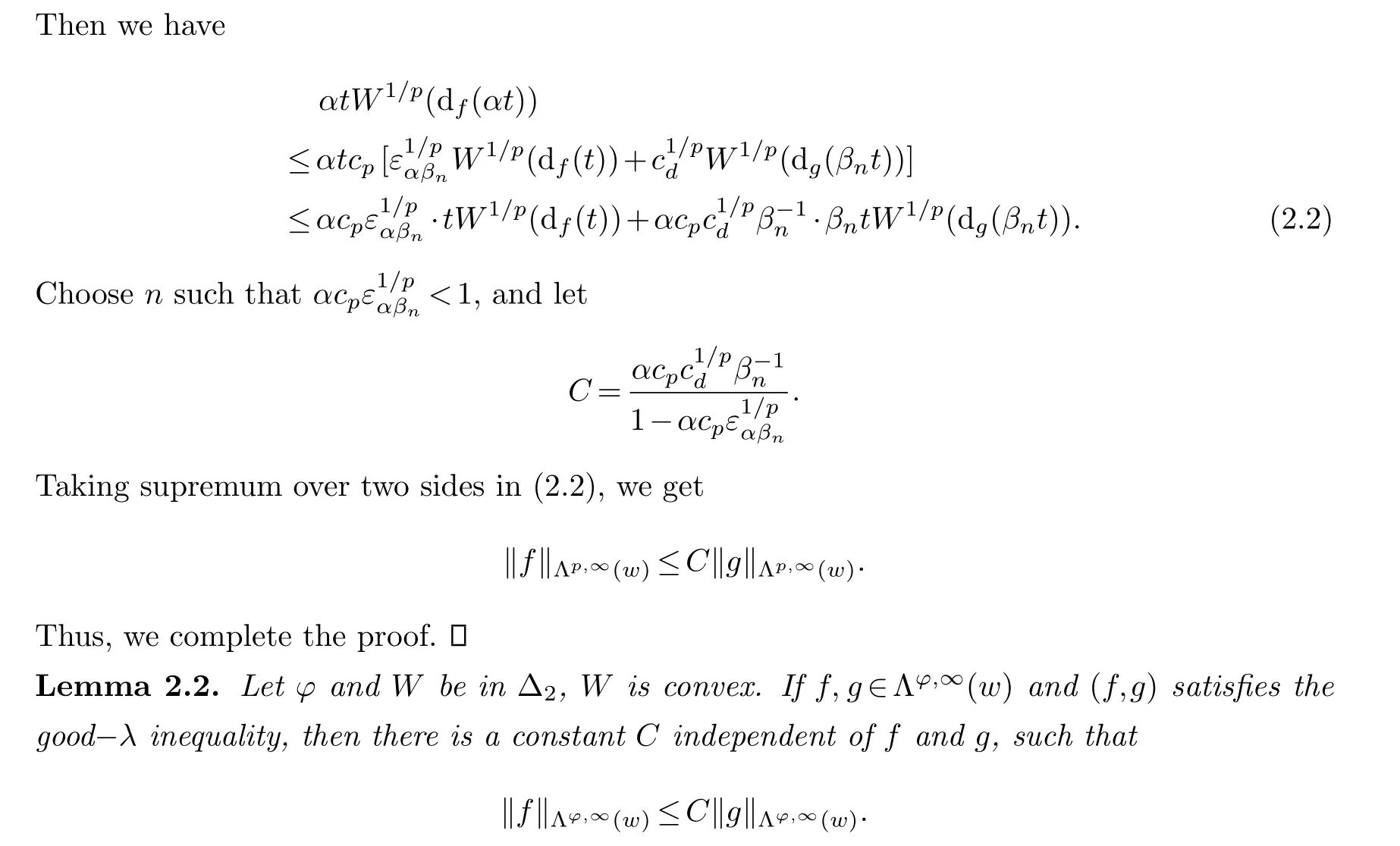


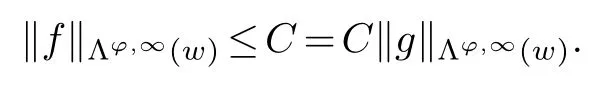



杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Finite Time Blowup with Upper Bound of Blowup Time of Solutions to Semilinear Parabolic Equations with General Nonlinearity
- Parameter Conditions for Hilbert-Type Operator Bounded with Homogeneous Kernels between Sequence Space l and Function Space L
- Expressions of Two Classes of Infinite Series in Terms of Bernoulli Numbers
- A Note on the Representation of an Integer in Two Different Bases
- Spatial Decay Estimates for the Solutions to Stokes Equations in Four Kinds of Semi-Infinite Cylinders
- Generalized Wave Operators in Von Neumann Algebras
