A Note on the Representation of an Integer in Two Different Bases

(School of Mathematics and Statistics,Henan University,Kaifeng 475004,China)

Abstract:Let a,b and n be integers larger than 1 and letα,βbe integers satisfying 0≤α25,which deepens the result of Stewart.

Keywords:Algebraic number;Bases;Digit

§1.Introduction

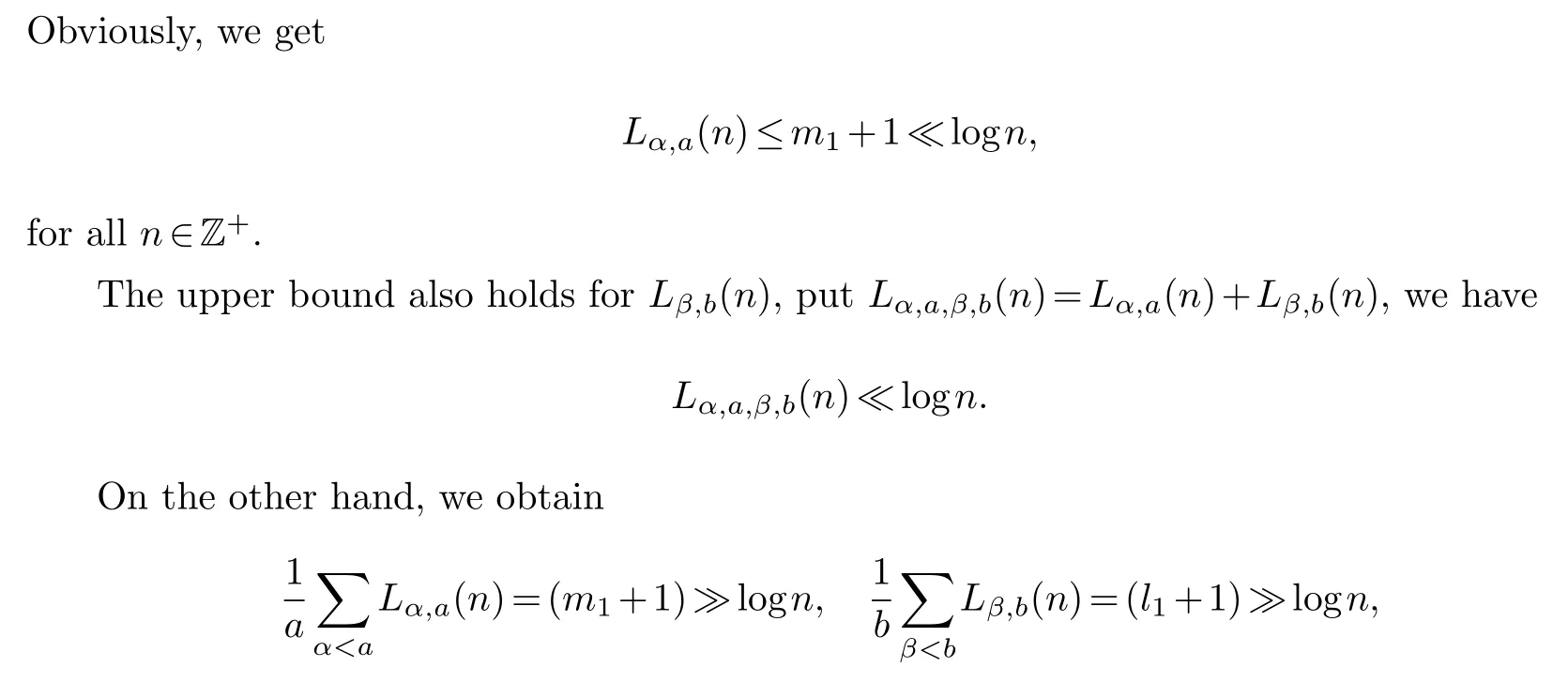
which means thatLα,a,β,b(n)≫lognholds on average.

It’s expected thatLα,a,β,b(n)≫lognindividually,which is not verified up to now.In 1979,Stewart[4]considered this problem and got the following result.

§2.Preliminary lemmas

In this section,we want to introduce two important Lemma for our Theorem.

Letb1,b2,...,bndenote rational integers with absolute values at mostBand letα1,α2,...,αndenote non-zero algebraic numbers with degrees at mostdand heights at mostA1,...,Anrespectively.We assume thatBandA1,...,Anare all at least 4.By the height of an algebraic number we shall mean the maximum of the absolute values of the relatively prime integer coefficients in the minimal defining polynomial of the number.We set

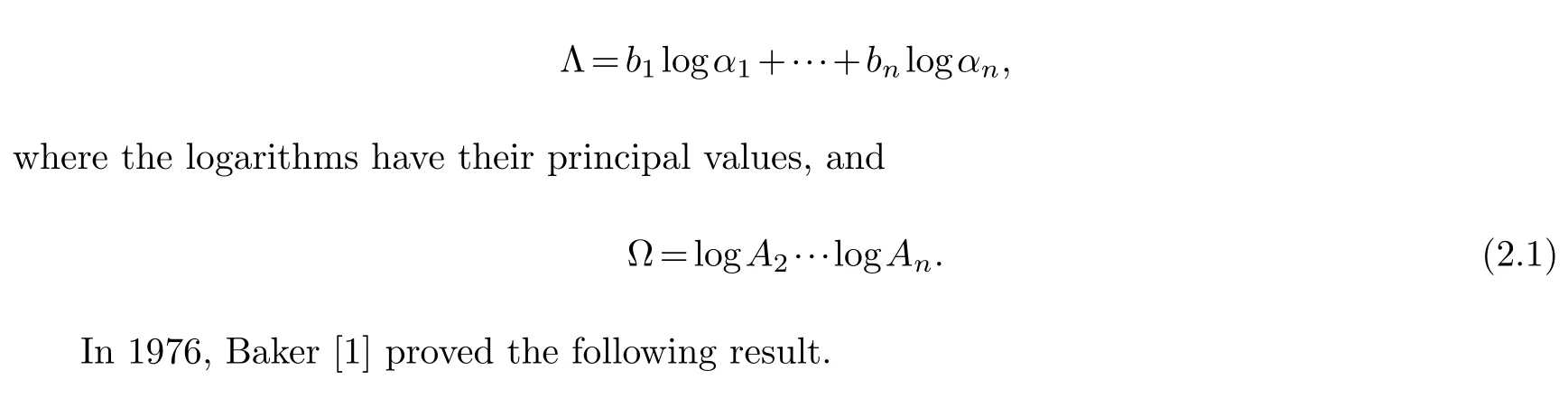
Lemma 2.1.IfΛ/=0then

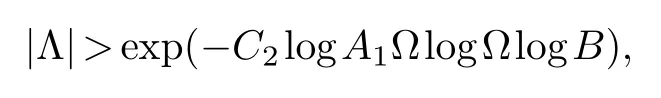
where C2is a positive number which is effectively computable in the terms of n and d only.

In the same year,Loxton and van der Poorten[5]investigated the degenerate situation whenΛ=0.They showed that ifΛ=0 then there exists a non-trivial linear dependence relation among the logarithms with integer coefficients which are small.

Lemma 2.2.Assume that A1≤A2≤···≤An,that b1,...,bn are not al l zero and thatα1,...,αn are positive real numbers.IfΛ=0then there exists a relation

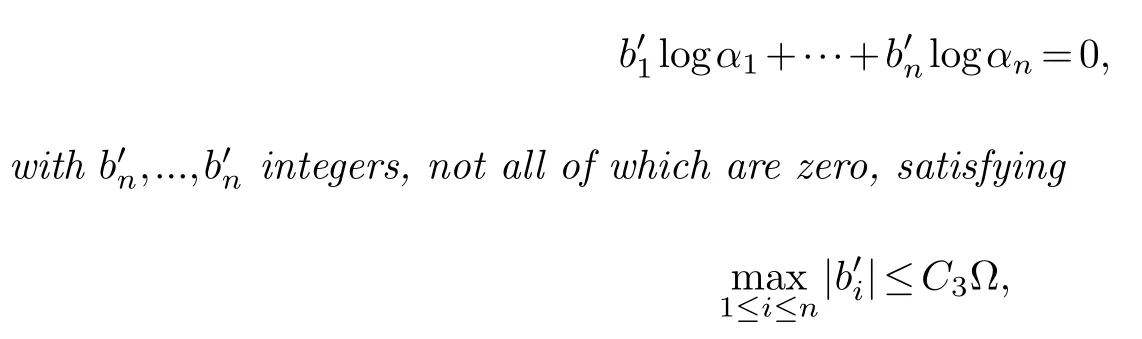
where C4is a positive number which is effectively computable in terms of n and d only.

§3.The proof of Theorem 1.2

As in the proof of Stewart Theorem,we consider the following two expansions ofn.

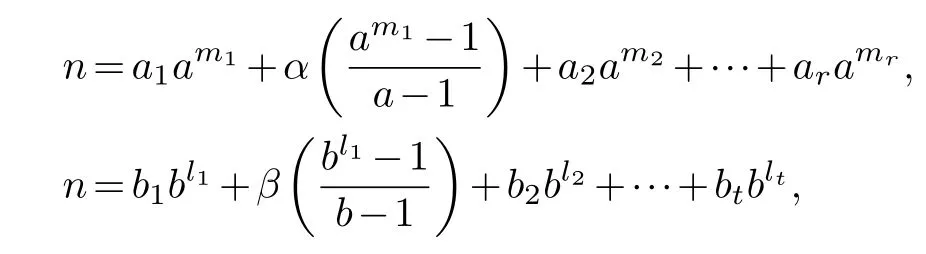
where 0≥lt≥0.

whereC′(will be introduce in the following part)is an absolute constant.

We now regard the intervalsΘ1=(0,θ],Θ2=(θ,θ2],...,Θk=(θk−1,θk],whereksatisfies the following inequalities

For intervalsΘs,1≤s≤k,we divide it into two cases.

Case 1.If each intervalΘs,fors=1,...,k,possesses at least one term either of the formm1−mior of the forml1−lj,then

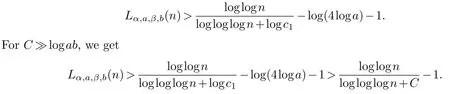
Case 2.Now we may assume that there exists an integers,with 1≤s≤k,for whichΘscontains no numbers of the formm1−miorl1−li.Definepandqby the inequalities