Generalized Wave Operators in Von Neumann Algebras

(School of Mathematics,East China University of Science and Technology,Shanghai 200237,China)

Abstract:Let M⊆B(H)be a countable decomposable properly infinite von Neumann algebra with a faithful normal semifinite tracial weightτwhere B(H)is the set of all bounded linear operators on Hilbert space H.The main purpose of this article is to introduce generalized weak wave operatorsgeneralized weak abelian wave operatorsand generalized stationary wave operators U±in M and then to explore the relation amongand generalized wave operators W±.

Keywords:Generalized wave operators;Von Neumann algebras;Generalized weak wave operators;Generalized stationary wave operators

§1.Introduction

This paper is a sequel to[7].LetM⊆B(H)be a countably decomposable,properly infinite semifinite von Neumann algebra(see[2],[8-11]for more details)with a faithful normal tracial weightτwhereB(H)is the set of all bounded linear operators onH.In[7],Qihui Li and the coauthors gave an analogue of Kato-Rosenblum theorem in a semifinite von Neumann algebraMby showing the existence of the generalized wave operatorW±.It is well-known that wave operators play a very important role in mathematical scattering theory(see[6],[12,13]for more details).Hence the existence of wave operatorW±(H1,H)for densely defined self-adjoint operatorsHandH1onHis one of the main research topics in this area.Actually,there are several variations of wave operators,such as weak wave operators,abelian wave operators and stationary wave operators.The concept of generalized wave operators inMis first given in[7]based on the notion of norm absolutely continuous projections.So it is natural to ask whether we can extend those variations of wave operators to a von Neumann algebraM.

§2.Preliminaries and notation

LetHbe a complex Hilbert space andB(H)be the set of all bounded linear operators onH.In this article,we assume thatM⊆B(H)is a countable decomposable properly infinite semifinite von Neumann algebra with a faithful normal tracial weightτandA(M)is the set of densely defined,closed operators affiliated withM.

2.1.The unitary group and resolvent of a self-adjoint operator

The resolventRH(z)=(H−z)−1and unitaryUH(t)=exp(−itH)for a self-adjoint operatorHplay a very important role in this section and next section,so we recall their properties and relations here.

Let{(EH(λ))}λ∈Rbe the spectral resolution of the identity forH.Forf,ginH,the unitary groupU(t)=UH(t)=exp(−itH)has the sesquilinear form

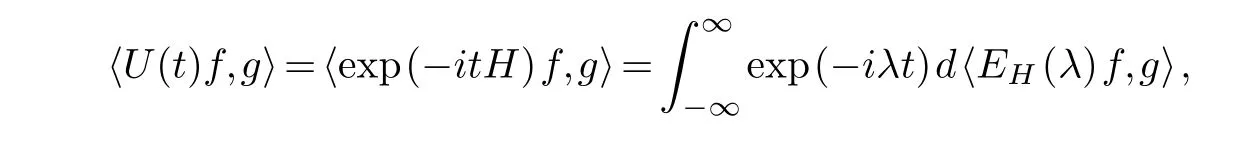
which is the Fourier transform of the spectral measure.Similarly,its resolventR(z)=RH(z)=(H−z)−1has the sesquilinear form

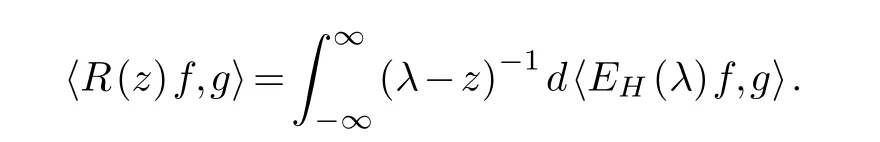
The connection between above two sesquilinear forms is given by the relation

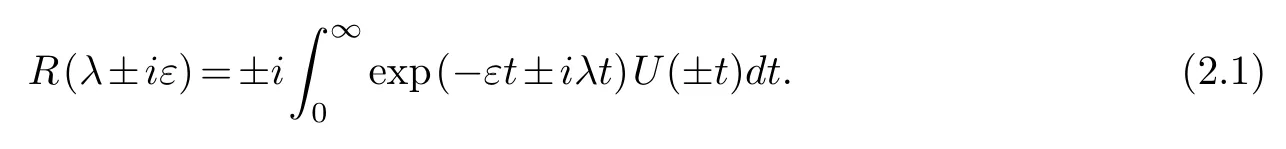
The proof of equality(2.1)is based on Fubini’s Theorem and given in Section 1.4[12].We set

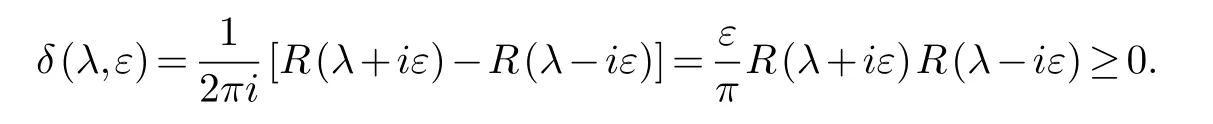
It implies that

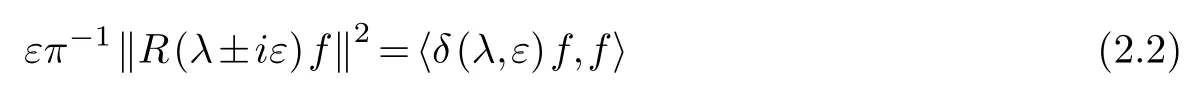
and

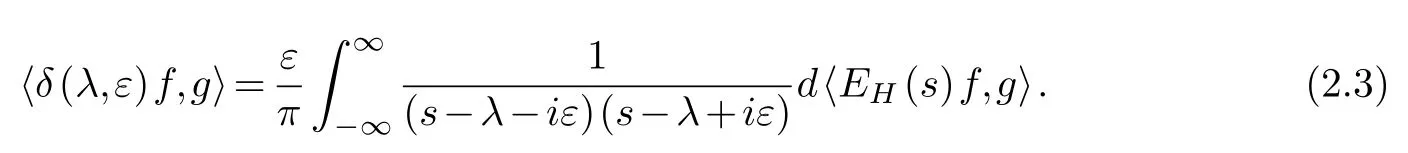
LetHac(H)be the set of all vectorsf∈Hsuch that the mappingλ−→〈EH(λ)f,f〉withλ∈R is a(locally)absolutely continuous function on R(see[6]or[12]for more details).From the argument in Section 1.4[12],we conclude that

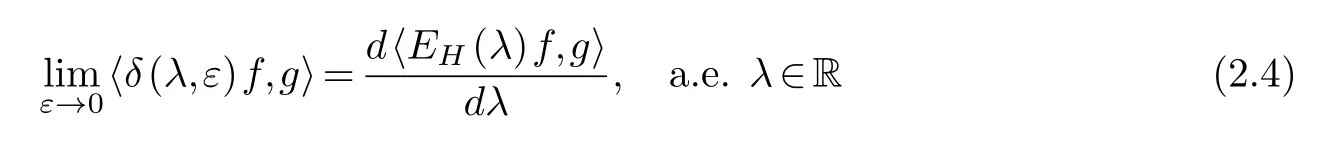
forforginHac(H).

2.2.Generalized wave operator in M

Before giving the definition of generalized wave operators,we need to introduce the following concepts which appear first in[7].

provided that s.o.t(strong operator topology)limit exists.

We note that the relation containing the signs”±”is understood as two independent equalities.

We will list a useful property ofW±(H1,H;J).SetWJ(t)=eitH1J e−itHfor eacht∈R.After slightly modify the proof of Theorem 5.2.5 in[7],we can get the following result.

Theorem 2.1.Let H,H1∈A(M)be a pair of self-adjoint operators and J be an operator inM.If W±(H1,H;J)exists for a pair of self-adjoint operators H,H1and J,then for any Borel functionφ

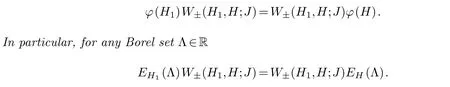
§3.Relation among±,±,U±and W±

3.1.Generalized weak wave operator W±in M

Definition 3.1.(generalized weak wave operator)Let H,H1∈A(M)be a pair of self-adjoint operators and J be an operator in M.The generalized weak wave operator for a pair of self-adjoint operators H,H1and J is the operator

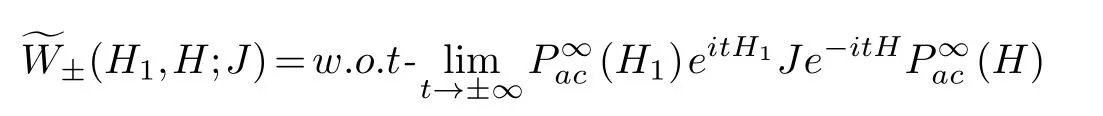
provided that w.o.t(weak operator topology)limit exists.

The idea of giving the definition of generalized stationary wave operators inMis same as the idea given in Section 2.2 of[12].So we summarize it here briefly.

Suppose that a nonnegative functionω(t),t≥0,is normalized by the condition

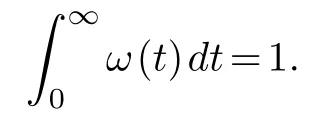
We introduce the averaging kernelωε(t)=εω(εt),ε>0.Generalized weak abelian wave operator±is defined by the equality

Remark 3.1.Letθ(t)=1as t≥0andθ(t)=0for t<0.We apply Placherel’s Theorem for Fourier transformation on Hilbert space(see Theorem 1.8.1 in[1])to the functions

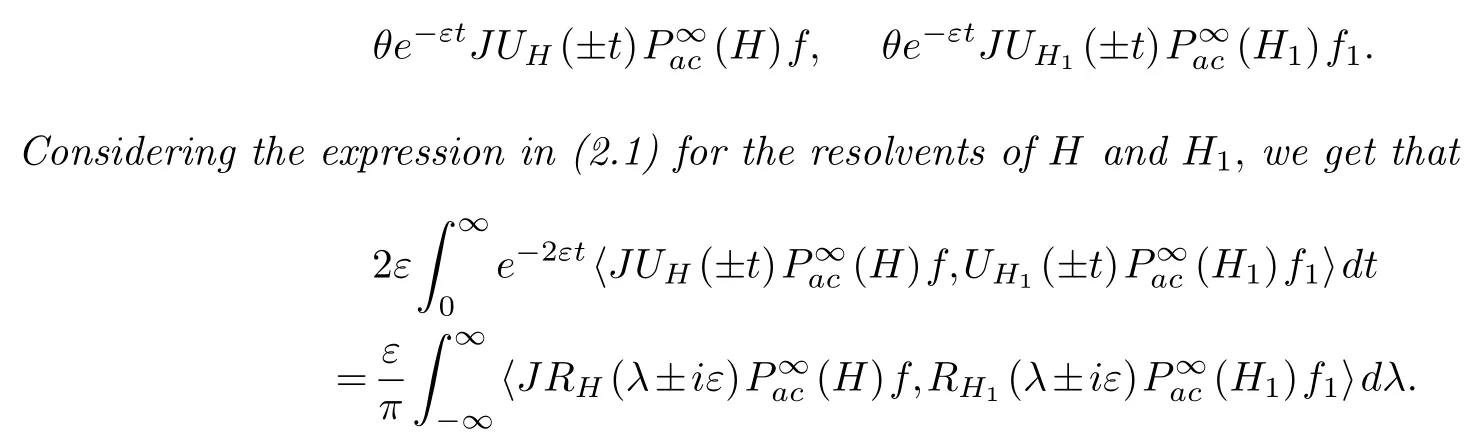
From the above argument,we can get the following result.

3.3.Relation among U±,~U±, W±and W±