汽油机活塞冷却喷射两相流及传热分析
2022-04-13张小矛王艳军
丁 宁,徐 政,陈 明,张小矛,王艳军,许 睿
(1.上海汽车集团股份有限公司技术中心,上海 201804;2.上海市汽车动力总成重点实验室,上海 201804)
0 概述
随着现代汽油机技术向小型化、增压化、高效化趋势发展,对活塞等重要零部件的热负荷提出了更高的要求。活塞的热量分布不合理不仅会导致自身的热失效问题,而且会影响缸内燃烧,产生积炭、早燃、爆震等非正常燃烧现象[1-5]。近年来除小部分低速小功率汽油机仍采用自然风冷的方式冷却活塞外,绝大多数汽油机仅靠活塞环、活塞裙部的热传导和活塞内腔气体对流散热已不能满足冷却要求,需采用活塞冷却喷射的方法进行强制冷却。其中,内腔强制冷却和内冷油道强制冷却成为了两个重要发展方向[6-7]。内腔强制冷却是通过活塞冷却喷嘴将机油喷射到活塞底部的内腔中,通过流动和传热过程将热量带走;内冷油道冷却是将机油直接喷射到内冷油道中,机油在内冷油道中振荡流动,吸收热量后由出口流出,降低活塞温度。
文献[8]中使用有限元法研究了内冷油道对活塞温度分布、应力分布和变形分布的影响,并通过FIRE软件稳态流动模拟计算得到了内冷油道的边界条件。在活塞顶边界采用的是零维燃烧时间平均处理方法,活塞环槽、销孔、裙部和内腔的边界均采用了经验或半经验方法。文献[9]中应用了ANSYS FLUENT软件结合流固耦合的方法研究了一款柴油机的活塞传热过程、瞬态运动过程及活塞内冷油道中的机油流动和油气分布。
文献[10]中运用了有限元软件FEMFAT 中的BASIC 模块对一款船用柴油机活塞进行了热机耦合仿真,对活塞的传热和温度场进行了深入的分析,探讨了实际运行工况下出现活塞顶烧蚀、开裂的原因。文献[11]中在建立活塞裙部型线、活塞优化后的燃烧室及内冷油道等的有限元模型之后,运用PERMAS 软件计算了优化后的活塞在标定工况下的温度场和热机耦合应力,并分析了活塞的疲劳寿命。
以往由于分析软件和分析方法的局限,上述研究主要集中在活塞的传热和温度分布领域。对于活塞冷却喷射的过程鲜有涉及,仅利用经验方法获得边界。活塞冷却喷射是一个十分复杂的气液两相流问题。该物理过程发生在高速运转的发动机曲轴箱内部,具有高速性、瞬态性、复杂性。如果不考虑机油的瞬态喷射过程,传热分析中缺少了机油的落点、流速、分布等诸多方面的因素影响,必然会与实际情况有所偏差。
本文中基于一款排量为1.5 L 的增压直喷汽油机,利用计算流体动力学软件CONVERGE 搭建了活塞冷却喷射两相流及传热分析模型。结合发动机实际运行工况,对比研究了内冷油道强制冷却、内腔强制冷却和活塞自然对流冷却等3 种活塞冷却方案。本研究可为发动机活塞设计及活塞冷却喷嘴选型提供重要的理论依据。
1 计算模型的建立
1.1 研究方案介绍
以车用4 缸汽油机为基础,在高速瞬态运动工况下深入研究活塞冷却喷射的油束运动发展过程及不同活塞冷却方式对传热的影响,具体包含了表1中的3 个研究方案。图1为活塞及其冷却喷嘴的几何模型。其中模型A 与模型C 采用同样的活塞和活塞冷却喷嘴,区别在于是否有活塞冷却喷射,通过两个方案的对比可以研究冷却喷射对活塞温度场的影响。模型B 采用了相同流量的活塞冷却喷嘴,但是活塞无内冷油道,采用传统的内腔强制冷却方式,其他结构参数均不变,通过与模型A 的对比可研究两种冷却方式的差异。
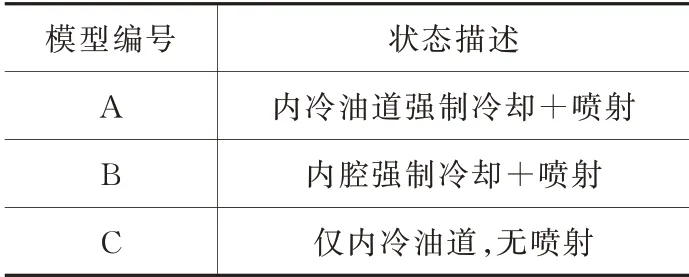
表1 研究方案

图1 活塞及其冷却喷嘴的几何模型
1.2 仿真建模
基于三维流体分析软件CONVERGE,建立了活塞冷却喷射和传热的单缸计算流体动力学(computational fluid dynamics,CFD)分析模型。该分析模型包含了曲轴、连杆、缸套、活塞、活塞冷却喷嘴、曲轴箱(局部)、油底壳(局部)等零部件,如图2所示。
该计算的基础网格为4 mm,对活塞冷却喷嘴及活塞内冷油道等位置进行了区域加密。实际的曲轴箱窜气入口在活塞余隙当中,因为厚度特别小(仅为0.4 mm),如果计算中设置成进气入口(随着活塞进行往复运动),即便进行一些加密,在气流运动比较快时仍容易导致计算收敛很慢,甚至出现计算发散。本文中将进气入口移动到了活塞的侧面,这样进气入口流体网格质量改善,计算速度加快了,稳定性也增强了。对比后发现两方案对喷射和传热影响较小,因此采用该简化方法进行进一步研究;同时为了防止润滑油回油之后残留在油底壳里从而影响计算收敛速度,将排气出口设置在油底壳底面,油滴落到出口即消失,大大提高了计算效率。对于活塞冷却喷嘴,本文不考虑分析其全部的结构,模型中仅包括其阀门以后伸入曲轴箱内的管路部分。
1.3 边界条件
本文针对一款排量为1.5 L 的小型增压汽油机在6 000 r/min 全负荷的运行工况进行CFD 仿真分析,该工况下窜气流量和活塞冷却喷嘴喷射流量均采用试验数据。为了保证曲轴箱内流场稳定和分析的可靠性,进行了4 个周期的计算,取最后一个周期的计算结果进行分析。具体边界条件如表2所示。
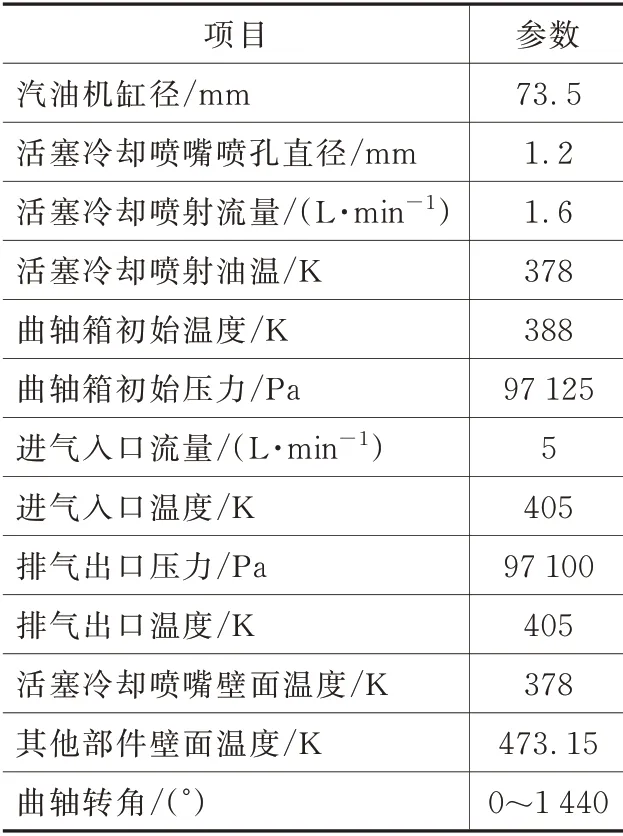
表2 边界条件
2 物理模型及验证
2.1 物理模型
活塞冷却喷射过程是一个非常复杂的瞬态两相流问题[12]。冷却机油和曲轴箱内的气体在高速中相互影响,并且一起进行周期性的运动。准确模拟活塞冷却喷射中的油束发展过程对于优化油气分布和后续传热效果至关重要。
本文中运用CONVERGE 软件中的高分辨率相界面流体体积函数(high-resolution interface capturing volume of fluent,HRIC VOF)对喷射过程进行求解。在该模型中可以考虑气相和液相之间的动量和能量交换,通过两相间的交互面进行数据的耦合,可以追踪到每个计算网格中的气液体积比例。
在HRIC VOF 模型中,用体积分数α来表示每个计算网格中的气液两相的比例。当α=0 时,表示网格内仅存在液相成分,也就是机油;当0<α<1 时,表示网格内既存在气相成分,也存在液相成分;当α=1 时,表示网格内仅存在气相成分。图3为计算网格中气液两相的划分。图中α值被圆形覆盖的区域代表该网格属于液相,其他的区域代表该网格属于气相。
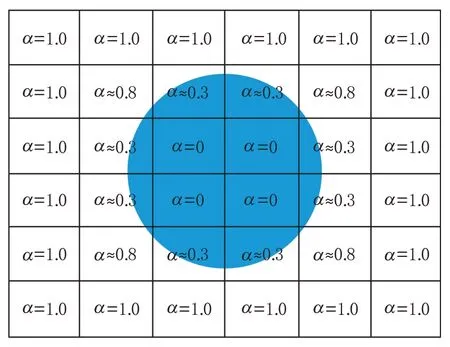
图3 计算网格中气液两相的划分
体积分数α可由守恒方程求解,如式(1)所示。
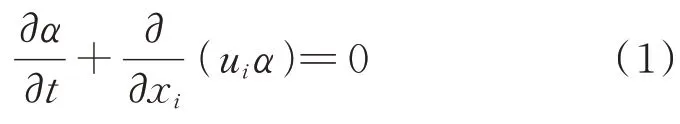
式中,t为时间;ui为速度,i=x,y,z;∂xi代表对x、y、z3 个方向求偏导。
网格中的整体密度ρ可由式(2)求解。
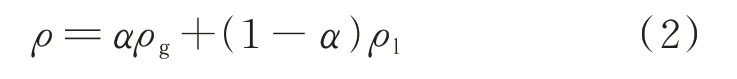
式中,ρg为计算网格中的气体密度;ρl为计算网格中的液体密度。
2.2 模型验证
在进行曲轴箱内的活塞冷却喷射瞬态计算前需要结合活塞冷却喷嘴出厂设计要求对喷射油束进行验证,即在稳定的流场的环境里校核打靶点,验证湍流、流体体积函数(volume of fluent,VOF)等物理模型的设置和计算网格的尺寸、数量设置,以保证后续在曲轴箱内强气流环境下喷射计算的准确度。
为此本文按照产品图纸要求建了一个圆柱型的计算流体域,其直径为40 mm,高度为101 mm,并在底部设置了孔径为5 mm 的小孔。按照产品设计要求,合格的活塞冷却喷嘴其油束需在喷射稳定后95% 以上穿过小孔。图4展示了该计算活塞冷却喷射的图像,图中油束稳定地穿过了小孔中心。图5显示了冷却液的喷射通过率。在喷射稳定后,大约有99.7% 以上的冷却液通过了小孔,证明了该计算物理模型设置合理,准确性满足要求。

图4 活塞冷却喷射油束验证(0.02 ms)
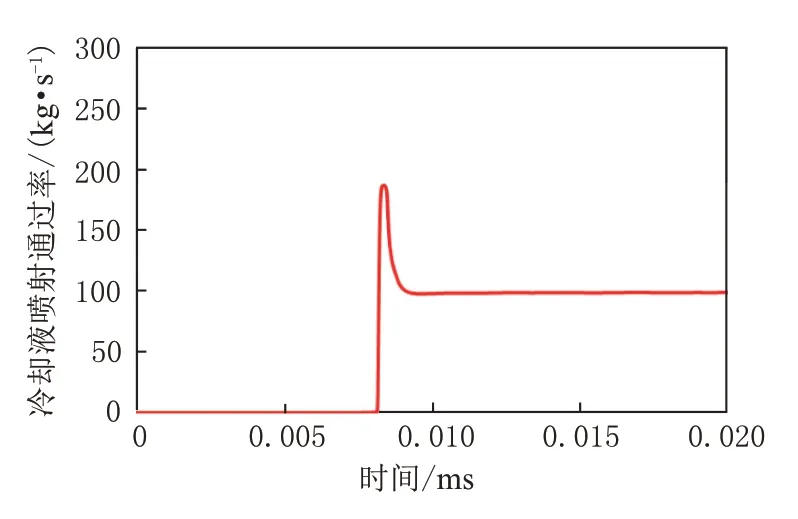
图5 冷却液喷射通过率
3 计算结果及分析
3.1 活塞冷却喷射油束分析
图6为模型A 的活塞冷却喷射图像的主视图和顶视图。从图中可知,不同的曲轴转角下,冷却机油在模型中的运动和发展规律是不同的。由于该模型中含有内冷油道,绝大部分机油被喷射到了内冷油道中,通过油道的两个方向向出口流动。很少部分的机油在曲轴箱内气流的干扰作用下喷射到了活塞的底部,没有能够进入内冷油道,见图6(i)与图6(j)。该部分燃油对于整体的冷却影响很小,可以忽略。进入内冷油道的机油随着活塞在内冷油道中振荡流动,吸收热量后从内冷油道出口流入曲轴箱,之后将有一部分机油与曲轴或连杆碰撞,被甩到缸壁和活塞底部,形成飞溅润滑。
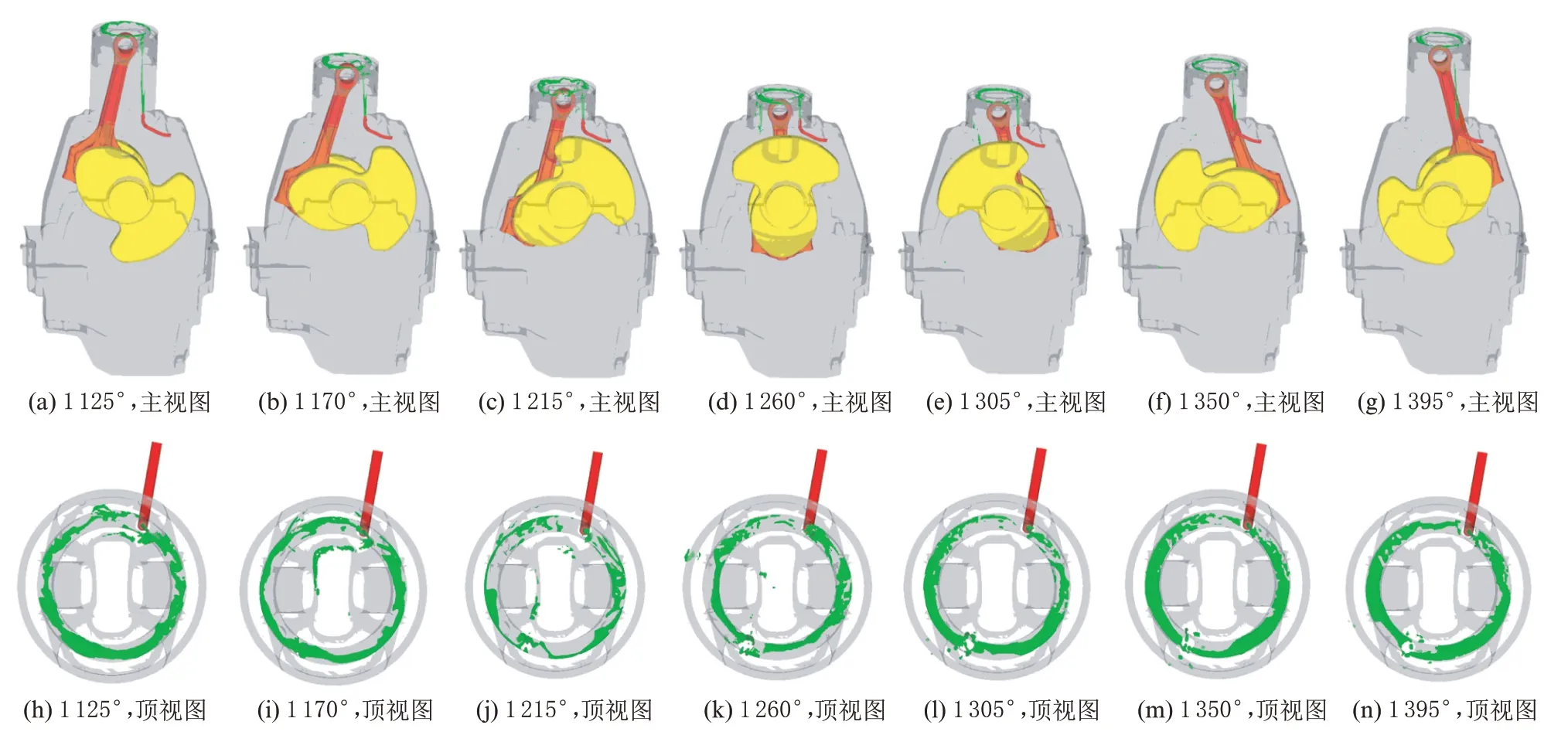
图6 模型A 的活塞冷却喷射图像
当活塞由上止点往下止点运动时,由于距离活塞冷却喷嘴越来越近,喷入活塞内冷油道入口的机油量逐渐增加。这一阶段,活塞经历了先向下加速再减速的运动过程。在前期加速运动过程中,由于活塞加速度大于重力加速度,机油会聚集在内冷油道顶部,几乎没有机油从内冷油道出口流出;在后期的减速运动过程中,在惯性的作用下,机油加速往下流动,使得大量的机油从内冷油道出口流出,尤其在下止点附近流出得最多,见图6(d)。
当活塞由下止点往上止点运动时,活塞先加速向上后减速运动。在1 340°~1 440°这一区间,没有机油能喷射到内冷油道的入口,这主要是因为该时间段活塞的平均运动速度大于喷射机油的平均运动速度,机油前锋面追不上活塞(图6(f)和图6(g)),因此在该时间段内冷油道内的机油量补充不足,流向出口的流动性变差,机油主要原地聚集在内冷油道的底部,流出出口的机油量很少。
图7为模型B 的活塞冷却喷射图像的主视图和顶视图。该模型采用了比较传统的活塞底部冷却方式。模型中不含内冷油道,因此机油的运动规律与图6有所不同。机油主要被喷射到了活塞底部的凹槽中,撞击凹槽壁面后,沿着凹槽向前后两个方向运动发展,冷却活塞底面后流入曲轴箱。同样,之后大部分机油与曲轴或连杆发生碰撞,甩出后形成飞溅润滑。
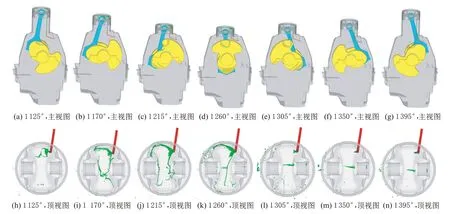
图7 模型B 活塞冷却喷射图像
当活塞由上止点往下止点运动时,由于距离活塞冷却喷嘴越来越近,撞击到活塞底部凹槽中的机油量和撞击强度都越来越大。有大量的机油向凹槽的前后两侧涌动,将活塞底部的热量带走。如图7(h)~图7(k)所示,由于活塞冷却喷嘴与活塞底部之间并不是完全垂直的,存在着一个夹角,在活塞的上下运动下,机油在活塞底部的落点呈线段式的往复运动,这就扩大了机油的冷却面积。
当活塞由下止点往上止点运动时,也存在着同样一个物理过程。活塞向上运动的平均速度大于机油向上运动的平均速度,机油前锋面追不上活塞的底部冷却面,无法对活塞底部进行有效冷却,见图7(f)与图7(g)。直到上止点后,活塞的运动方向发生了改变,机油赶上了活塞,继而开始一个新的冷却循环。
3.2 活塞冷却面传热分析
图8对比了模型A 与模型C 的内冷油道壁面平均传热系数随曲轴转角的变化规律。对于模型A,传热系数基本随曲轴转角呈周期性的变化。本文中的传热计算方法与大多数参考文献不同,考虑了活塞的往复运动和实际的活塞冷却喷射过程,而不是单独将内冷油道抽出来进行简化的稳态计算或者瞬态计算[8],这样计算结果更加符合真实的物理过程。通过前期的研究发现活塞运动对于内冷油道壁面的传热系数计算精度影响非常大。在该机6 000 r/min 的工况下,同样的模型如果不考虑活塞运动,机油就会在流道里运行地十分顺畅,相当于冷却液在内冷油道里的流速很高,传热系数可增加接近一倍。如果考虑了活塞运动,机油在内冷油道中就会有上下的振动,并且在入口、出口受到加速度的影响,造成补充、流动困难,极大地影响了冷却液绕油道的流动速度。虽然振荡也在一定程度上会提高冷却液的传热系数,但是前者在小型汽油机内冷油道传热系数的影响因素当中占据了更加关键的位置。
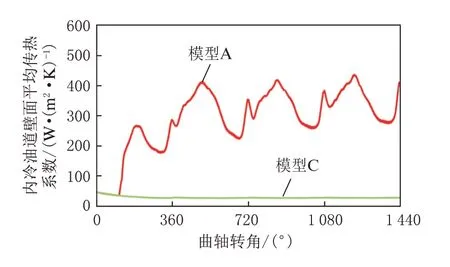
图8 内冷油道壁面平均传热系数曲线
本文中计算了4 个活塞运动循环。由于前3 个循环(0°~1 080°)曲轴箱和内冷油道内没有形成稳定的流场,传热系数不稳定,因此将主要研究最后1 个活塞运动循环。如图8所示,模型A 的传热系数变化趋势与上文冷却喷射油束分析结果比较吻合:(1)内冷油道壁面传热系数最大值为436 W/(m2·K),出现在活塞下止点(1 260°)附近。该处距离活塞冷却喷嘴最近,有大量机油涌入内冷油道的入口,也有很多机油在惯性的作用下流出。油道内的机油流动速度很快,提高了对流传热系数。(2)内冷油道壁面传热系数最小值为277 W/(m2·K),出现在1 394°,该处活塞处于由下止点向上止点的运动过程中,内冷油道入口没有机油补充,再加上活塞运动加速度较大,导致油道内机油流动性变差,对流传热系数降低。(3)内冷油道壁面传热系数在1 085°时出现一个明显的尖峰。该处活塞刚开始由上止点向下止点运动,机油前锋面即在该时刻追上了活塞。前期在空中积累的大量机油集中冲入了内冷油道入口,加速了流动和传热,因此形成了一个小的传热峰值。对于模型C,由于计算中只包含了气流运动,没有考虑机油冷却,因此内冷油道内的壁面传热曲线比较平稳,无明显的周期性,平均传热系数基本在28 W/(m2·K)左右。
图9展示了模型A 与模型C 的内冷油道壁面的对流传热系数分布。该传热系数分布是基于活塞最后一个循环的时间平均。由图9(a)可知,模型A的传热系数较大区域出现在内冷油道入口及周边位置,最大传热系数超过了1 000 W/(m2·K);内冷油道的环部及出口位置传热系数分布在200 W/(m2·K)~500 W/(m2·K)之间。由图9(b)可知,由于没有机油喷射,内冷油道内部仅是壁面与气流之间进行对流传热,模型C 的传热系数比较小,且非常均匀。
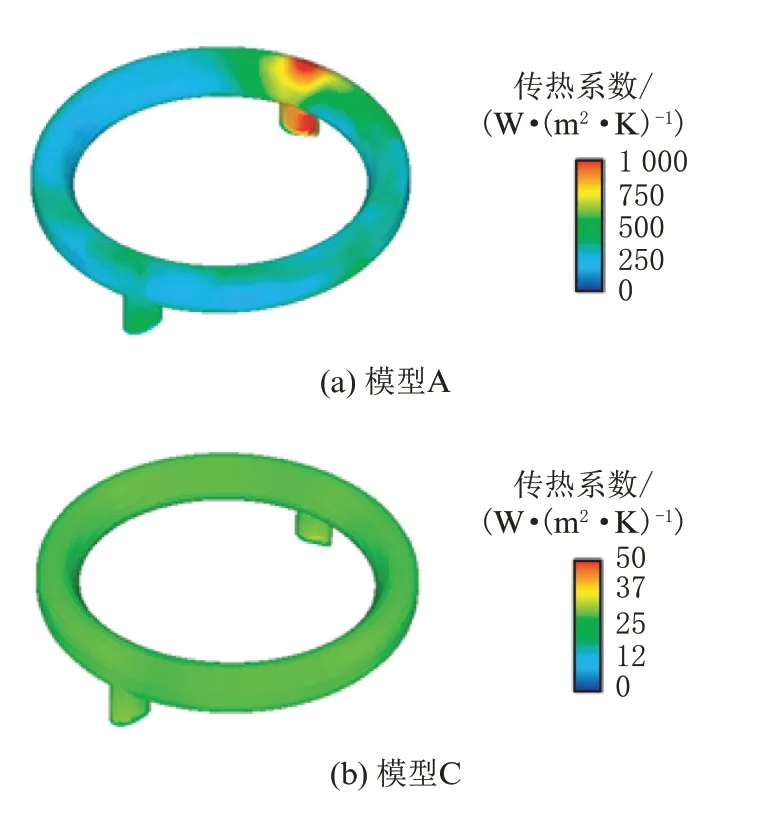
图9 内冷油道壁面的对流传热系数分布
图10对比了3 个模型的活塞底面的平均传热系数随曲轴转角的变化规律。图中结果均只考虑了活塞冷却喷射和曲轴箱内气流对流传热的影响,飞溅润滑等其他影响因素均不考虑在内。模型A 与模型B 的传热系数曲线均有明显的周期性,而模型C 的传热系数较低且比较平稳。模型A 与模型C 有同样的几何结构,而模型A 的底面对流传热系数高于模型C,这是因为有少量的机油没有喷入活塞内冷油道,而进入了底部的凹槽,形成了对活塞底部的冷却。模型B 中机油全部喷入活塞底部的凹槽,对活塞底面的冷却作用较大,最大传热系数可达206 W/(m2·K)。
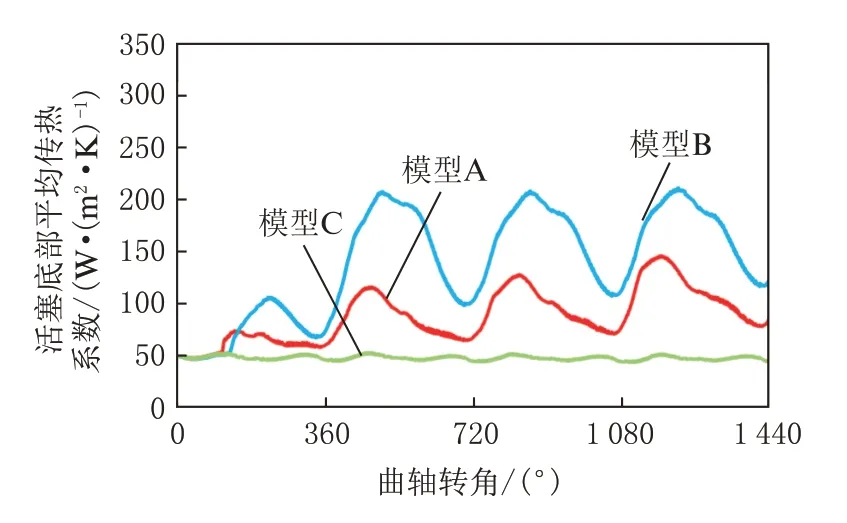
图10 活塞底面平均传热系数曲线
图11展示了3 个模型活塞底面的对流传热系数分布。由图11(a)可知,模型A 的传热系数较大区域出现在活塞底面靠近内冷油道入口和出口的位置,最大传热系数在50 W/(m2·K)以上,其余位置传热系数基本都在35 W/(m2·K)以下。由图11(b)可知,模型B的传热系数最大区域出现在油束落点及其运动扩散的周边区域,数值可达115 W/(m2·K)以上;底面其余位置的传热系数较低,平均在50 W/(m2·K)以下。由图11(c)可知,模型C 的底面传热系数比较均匀,且传热系数较小。
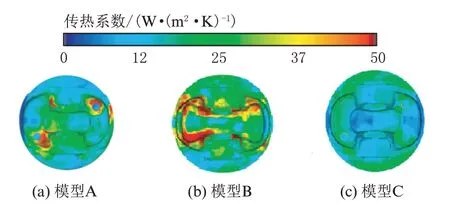
图11 活塞底面的对流传热系数分布
4 活塞温度测量及模型验证
本文中选用硬度塞测量法对模型A 关键位置进行了温度测量,并与模拟计算的结果进行对比,来验证传热和温度场计算的准确性[13-14]。硬度塞法的原理是金属材料受热后产生永久性的硬度变化,利用硬度塞的温度—硬度对应曲线即可测量温度。将选用的硬度塞材料加工成直径为2.5 mm、长度为4.2 mm 的紧固螺钉,分别拧入活塞各测点的位置,见图12。硬度塞与被测金属表面要求有很好的接触,以便能获得准确的温度。
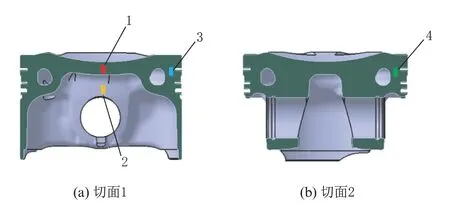
图12 模型A 活塞温度测点布置
发动机试验工况为6 000 r/min 全负荷工况,试验值与模拟值的对比见图13。试验温度与模拟计算温度能较好吻合,最大偏差仅为5.24%,由此可认为该分析方法比较合理。
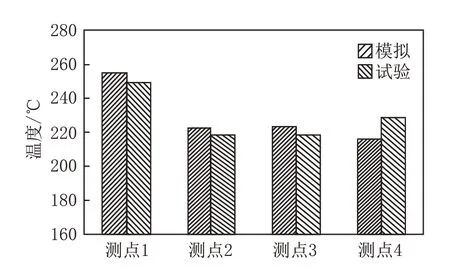
图13 模型A 活塞各测点温度对比图
5 各模型活塞温度场对比
本文中活塞温度场计算采用了通用结构分析软件ABAQUS 进行求解。计算中的流体边界包括了活塞顶面燃烧边界条件、内冷油道冷却边界、活塞底面冷却边界等部分。图14为活塞顶面燃烧边界条件,是用CONVERGE 软件针对燃烧系统进行两个循环计算结果的数值平均。本文中各模型均采用相同的活塞顶面燃烧边界条件,仅对比不同内冷油道和活塞底面冷却边界对温度场的影响。
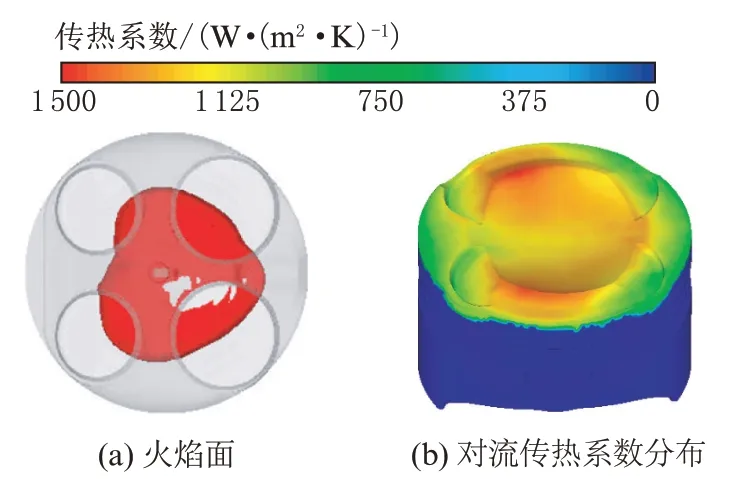
图14 活塞顶面燃烧边界条件
各活塞模型温度场分布见图15,关键部位最高温度值对比见图16。对比各模型,可以发现无论是内冷油道强制冷却、内腔强制冷却,还是活塞自然对流冷却,活塞表面的温度较高区域均出现在活塞顶面的中心略偏向进气侧,这是由于本文中采用CFD软件缸内燃烧计算的热边界,其缸内火焰传播规律对其传热分布有较大影响。活塞底部两侧边缘区域温度明显较低,这是因为它距离燃烧室顶面较远,燃烧传来的热量较少而冷却作用又比较强。
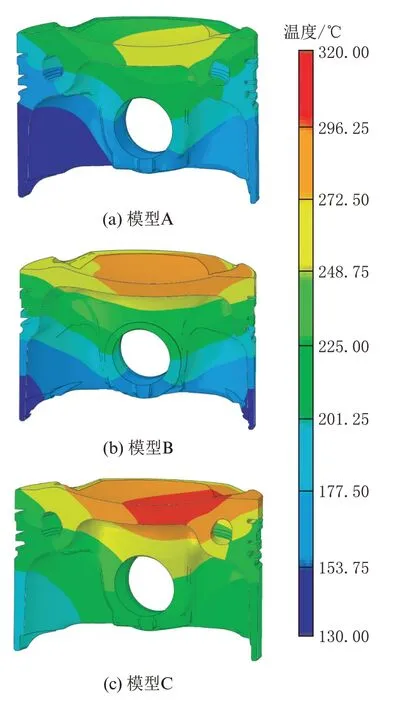
图15 各模型温度分布
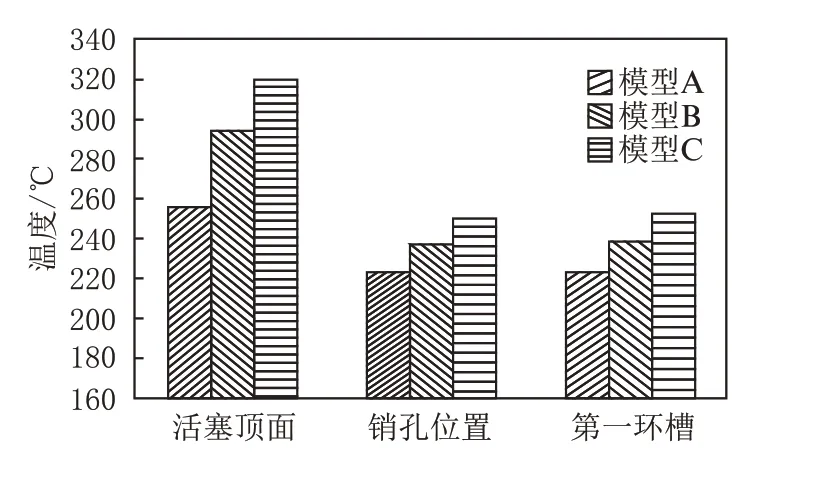
图16 各模型关键部位最高温度值对比
对比分析模型A 与模型B 可知,在相同的冷却喷射流量下,采用内冷油道强制冷却方式比采用内腔强制冷却方式活塞顶面最高温度可降低39 ℃,销孔位置最高温度可降低15 ℃,第一环槽的最高温度可降低16 ℃。可见采用内冷油道强制冷却可大幅度降低活塞关键部位的温度值,将显著改善活塞表面的积炭和结焦。
对比分析模型A 与模型C 可知,同样的活塞结构下,有内冷油道强制冷却喷射可使活塞顶面最高温度降低64 ℃,销孔位置最高温度可降低28 ℃,第一环槽的最高温度可降低29 ℃。由此可见内冷油道强制冷却方式对于降低活塞表面温度具有重要的作用。
6 结论
(1)采用模型A 的方案时绝大部分机油被喷射到了内冷油道中,通过油道的两个方向向出口流动。有极少部分机油在曲轴箱内气流的干扰作用下喷射到了活塞的底部,未进入内冷油道。采用模型B 的方案时机油主要被喷射到了活塞底部的凹槽中,撞击凹槽壁面后沿着凹槽向前后两个方向运动发展,冷却活塞底面后流入曲轴箱。
(2)对于内冷油道壁面的传热,模型A 的传热系数基本随曲轴转角呈周期性的变化,传热系数较大的区域出现在油道入口及周边位置;模型C 的传热系数比较小,且非常均匀。对于活塞底面的传热,模型B 冷却量较大,远远高于模型A 与模型C。
(3)采用了硬度塞测量法对模型A 关键位置进行了温度测量,并与模拟计算的结果进行了对比,最大偏差仅为5.24%,验证了传热计算的准确性。
(4)由各方案活塞温度场对比可知,在相同的冷却喷射流量下,采用内冷油道强制冷却方式的活塞表面最高温度比采用内腔强制冷却方式降低39 ℃,比采用自然对流冷却方式降低64 ℃。
