地铁列车荷载作用下砖石古塔振动响应研究

谢伟平，刘少武，许暮迪

(1.武汉理工大学 土木工程与建筑学院，湖北 武汉 430070；2.武汉理工大学 后勤保障处，湖北 武汉 430070)

随着近些年来地铁的迅速发展，其运行所造成的振动问题也日渐凸显，特别是当地铁规划线路周边存在古建筑时，这个问题更为严重。由于古建筑的特殊性，针对古建筑的振动研究尤为重要。有关轨道交通引发的环境振动问题已有大量研究[1-5]。可以发现，现有研究多集中在对现代建筑的研究而针对古建筑的振动研究相对较少。SA‐DEGHI等[6]建立有限元模型，研究了不同地质条件下古教堂与地铁线路间的安全距离。LACANNA等[7]通过实测对某古教堂在交通荷载激励下的振动安全性进行了评估。ERCAN[8]使用环境脉动测试数据校核有限元模型，分析了砌体结构古建筑的动力特性。马蒙等[9]通过数值计算，预测了多条地铁线路联合运行下西安钟楼的安全性。朱利明等[10]通过实测地铁开通前后不同环境下鼓楼的结构振动，分析了地铁运行对鼓楼安全性的影响。宣家棋[11]通过实测得到下夏河塔在高铁作用下的振动响应，评价了该塔的安全性。地铁荷载造成的振动属于弱振，在研究弱振时对模型的精细化程度要求较高，而目前大部分研究中所采用的数值计算模型是基于强震条件下建立的，没有考虑非结构给构件的影响，存在着模型精细化程度不足的问题，本文以洪山宝塔为研究对象，通过地脉动测试分析得到其自振频率和振型。引入土-古塔相互作用模型，并考虑古塔内部非结构构件，基于实测数据建立砖石古塔精细化模型，研究砖石古塔在地铁列车激励下的振动响应，讨论不同振动距离条件下古塔的安全性，为类似砖石古塔的保护工作提供参考。

1 试验概况

1.1 洪山宝塔简介

洪山宝塔建成于公元1291 年。塔体由砖石砌成，塔身共7 层，通高44.1 m，基宽37.3 m，其外观如图1(a)。塔各层构造相似，塔体横截面为近似正八边形。该塔各层有4条券洞，两两对称布置且上下隔开，于楼板处分别对称向上和向下斜向穿透墙体，如图1(b)所示。塔刹为铁制，约重6 500 kg。

1.2 测点布置

测点布置参照国家规范[12]中的规定，测试时将测点布置在测试层塔室的楼板中心处进行同步地脉动测试。由于传感器的数量有限，每轮测试时先在选定的1，3，5 和7 层的塔室内各布置东西朝向的传感器(各层测点位于同一投影点上)，共4 个传感器，记为P1-P4。待测完后在同一位置将传感器变换为南北朝向，记录测点为P5-P8。测点示意图如图2所示。

1.3 测试工况

在选定测试楼层进行地脉动测试，记录地脉动作用下宝塔在2个不同水平方向的加速度值。测试中，选定一个方向后进行同步测试，同时测试第1 层，3 层，5 层和7 层的水平加速度。第1 轮测试，将传感器布置为东西朝向，进行2次试验，每次试验持续测试30 min。待第一轮测试结束后，将传感器换为南北朝向，进行第2轮测试。为确保无其他振动信号的干扰，在测试过程中，古塔周边区域禁止车辆和游客进入，保证测试环境达到要求。

2 试验结果分析

2.1 自振频率分析

由于地脉动为随机荷载，则由随机振动理论识别宝塔的自振频率：

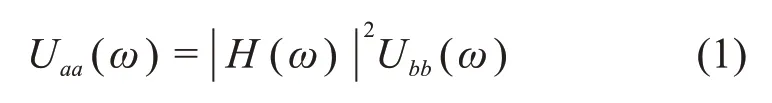
其中：Uaa(ω)为结构自功率谱；Ubb(ω)为地脉动自功率谱；H(ω)为传递函数。由于地脉动与有限带宽白噪声的特性非常相似，则在有环境干扰致使无法准确获取输入信号的情况下，可将输入信号的功率谱Ubb(ω)作为常数U，由此可得到：

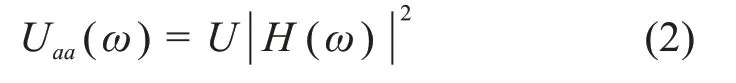
式(2)说明由结构自功率谱可以得到结构自振频率。对测试结果进行自功率谱变换，得到图3曲线。本文在进行互功率谱、相干函数、相位处理时，均以第7 层测点为参考点，处理结果如图3～5。由于篇幅所限，仅列出一组东西向测点的处理结果。由图3～5 可以发现，自功率谱和互功率谱频率峰值相近，同时在峰值频率处相位角近似相同或呈180°，且相干函数均大于0.8，符合结构模态频率识别标准[13]，说明图中峰值是古塔前2 阶自振频率。表1 为前2 阶自振频率实测结果，可以发现由于洪山宝塔的结构具有良好对称性，2 个方向的各阶自振频率极为接近。

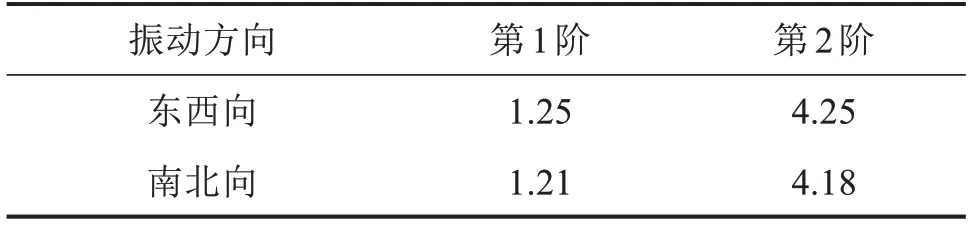
表1 洪山宝塔自振频率测试结果Table 1 Test results of natural vibration frequency of Hongshan pagoda

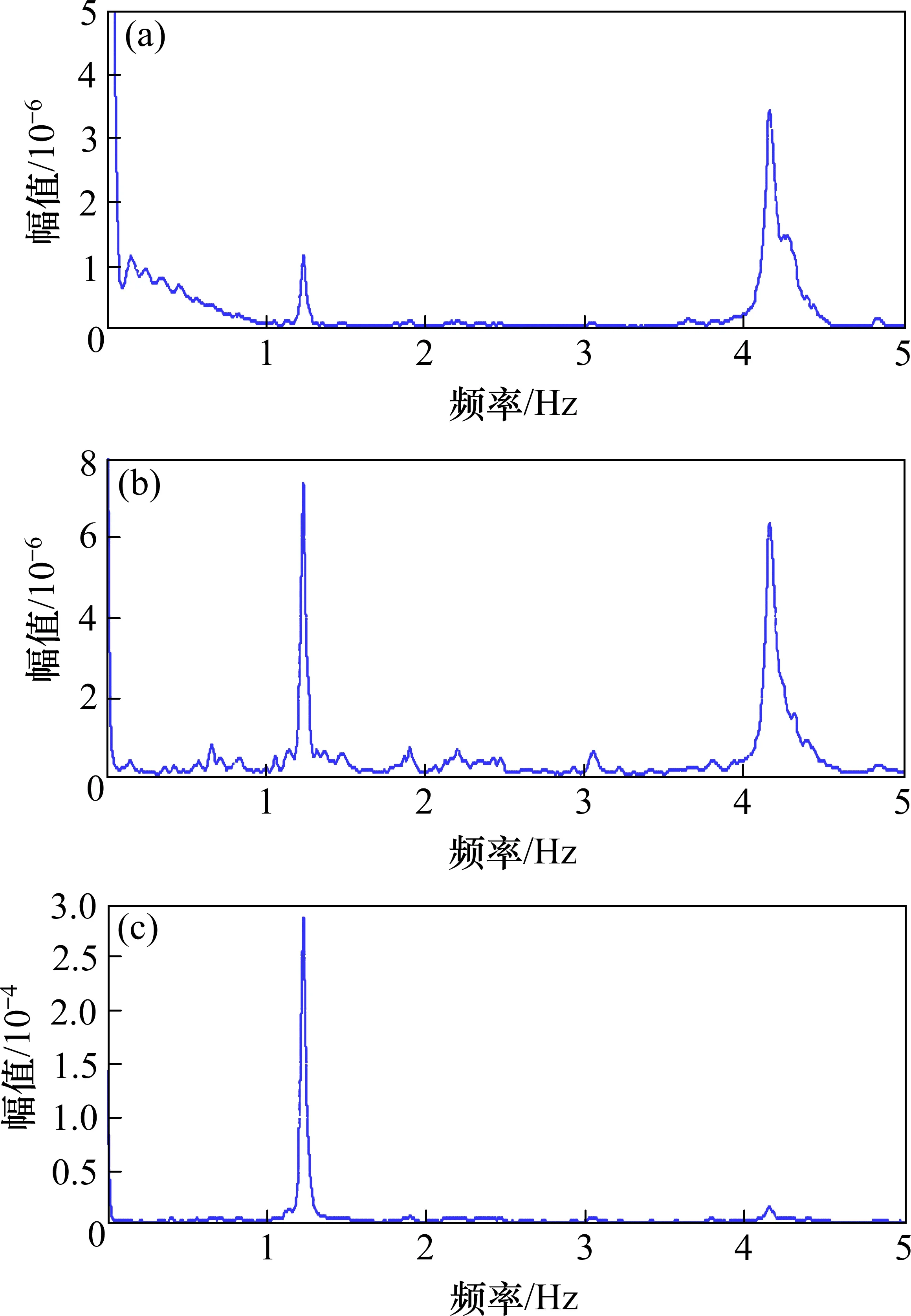
图3 东西向测点自功率谱Fig.3 Auto-power spectrum of measuring points,E-W

图4 东西向P2与P4测点互功率谱、相位和相干函数图Fig.4 Cross-power spectrum,phase diagram and coherence function diagram of P2 and P4,E-W

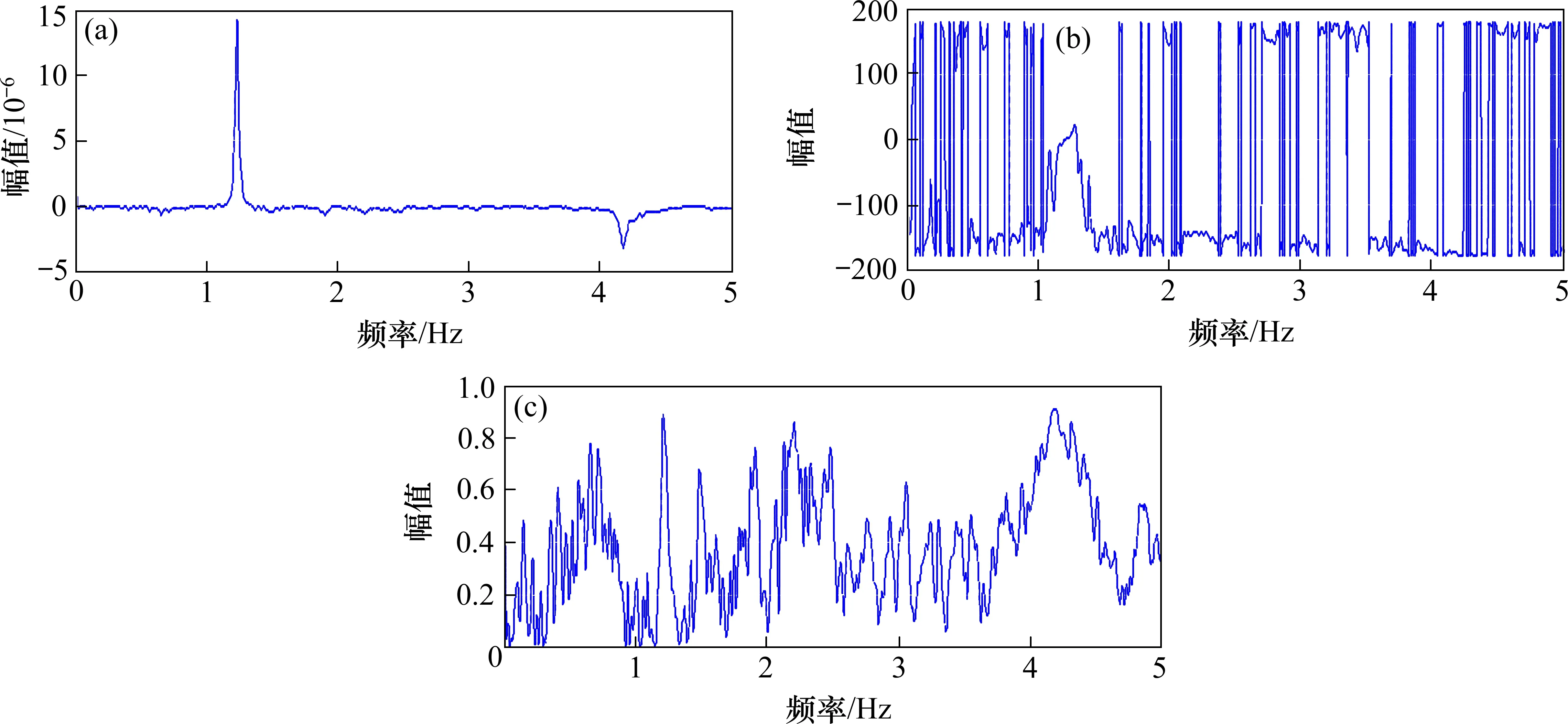
图5 东西向P3与P4测点互功率谱、相位和相干函数图Fig.5 Cross-power spectrum,phase diagram and coherence function diagram of P3 and P4,E-W

2.2 振型分析

将古塔视为一个多质点体系，各测点的第k阶振动坐标与功率谱的关系如下[14]：

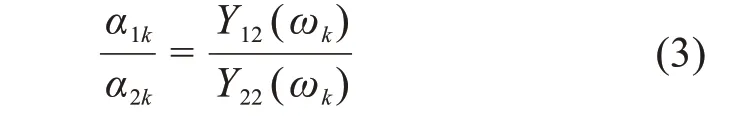
式中：α1k和α2k分别2个考察点的第k阶振型坐标Y22(ωk)为考察点2的自功率谱峰值；Y12(ωk)为2个考察点的互功率谱峰值。由式(3)计算洪山宝塔的振型坐标，得到洪山宝塔沿水平方向振动的前2阶振型如图6 所示。可以看到宝塔在2 个方向的前2 阶振型均非常相似。

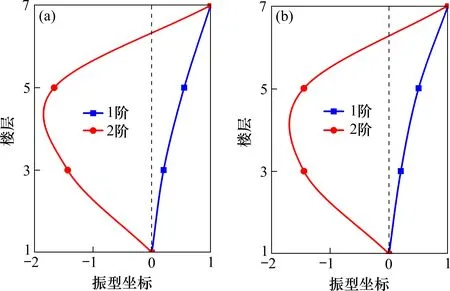
图6 古塔前2 阶振型图Fig.6 First two modes of the pagoda

3 有限元模型的建立

3.1 模型简介

本文根据古塔的结构特点，按照结构实际尺寸建立有限元实体模型，模型细节如图7所示。模型中塔身部分使用Solid65 单元进行模拟，塔刹用Solid185 单元模拟。模型为提高模型精细化程度，建立了沿塔内壁布置的楼梯、楼梯护墙以及塔基等结构。上述结构也均使用Solid65 单元模拟。同时，不同于之前大部分研究中的古建筑模型，模型通过引入地基弹簧，模拟了土—古塔的相互作用。该模型中在模型的基础下表面采用弹簧单元建立了Winkler 弹性地基模型，通过辅助表面单元可以计算出每个弹簧单元的刚度。通过实测可得地基弹性模量值取30 MPa。

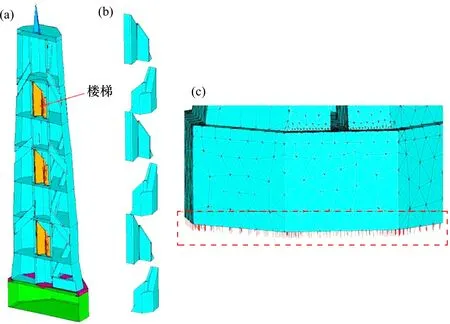
图7 洪山宝塔有限元模型Fig.7 Finite element model of pagoda

3.2 模态与振型校核

由于洪山宝塔是文物保护建筑，因此不能对宝塔进行破坏性试验。参考文献[15]中的取值，取多组材料属性进行试算，对照上文中的实测结果，得到最佳取值组合，材料属性如表2所示。

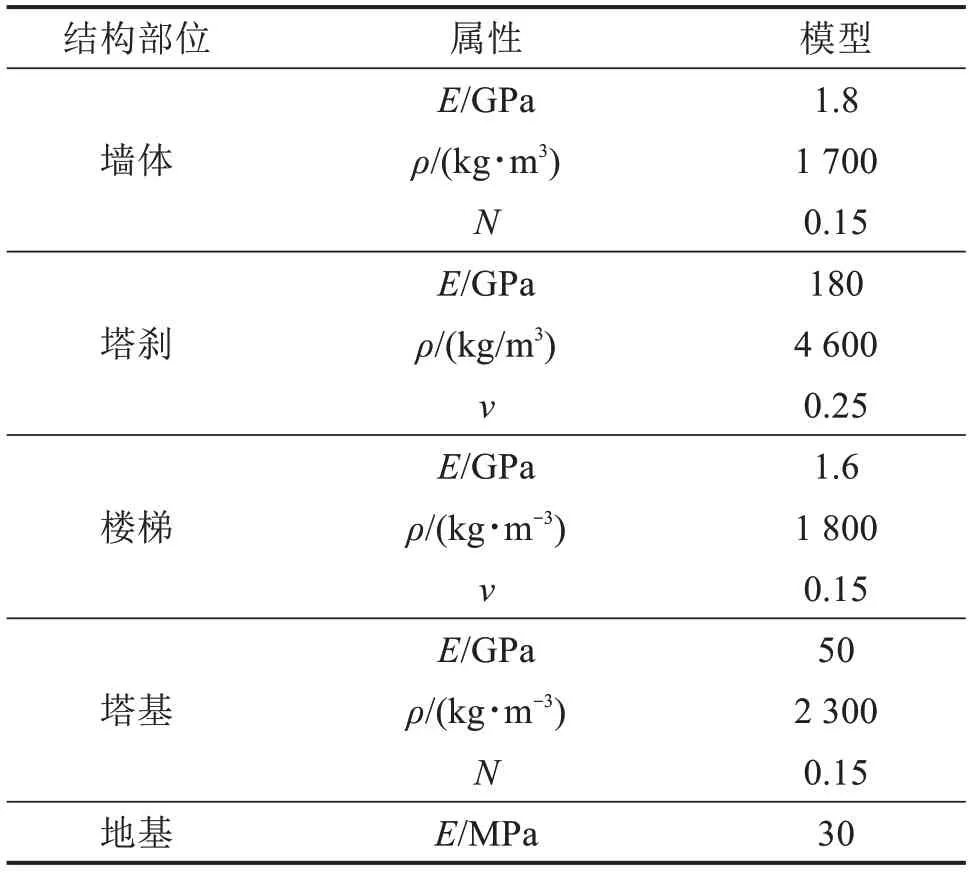
表2 洪山宝塔模型材料属性Table 2 Model material properties

经过模态分析后，得到计算结果为：东西向和南北向第1 阶频率分别为1.17 Hz 和1.22 Hz；东西向和南北向第2阶频率分别为4.78 Hz和4.88 Hz。可以发现自振频率的测试值与模拟值的差值很小。因塔内沿塔壁建设的楼梯均布置在东西两侧塔壁，对东西向的刚度带来一定影响，使东西向的频率计算结果略高。

图8 为振型模拟结果图。由于2 个方向模拟结果相近，故本文仅列出东西向模拟结果。由图可知，2 个方向的前第2 阶振型皆为平动。图9 为实测和模拟振型的对比图，可以发现振型模拟结果良好。

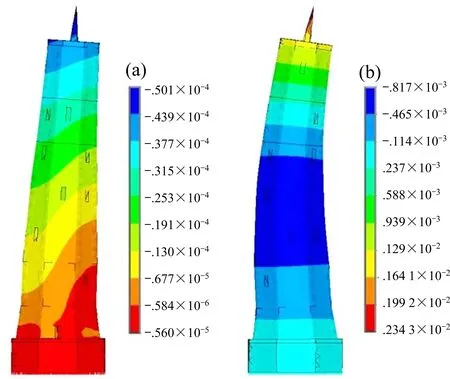
图8 宝塔振型模拟Fig.8 Result of modal simulation

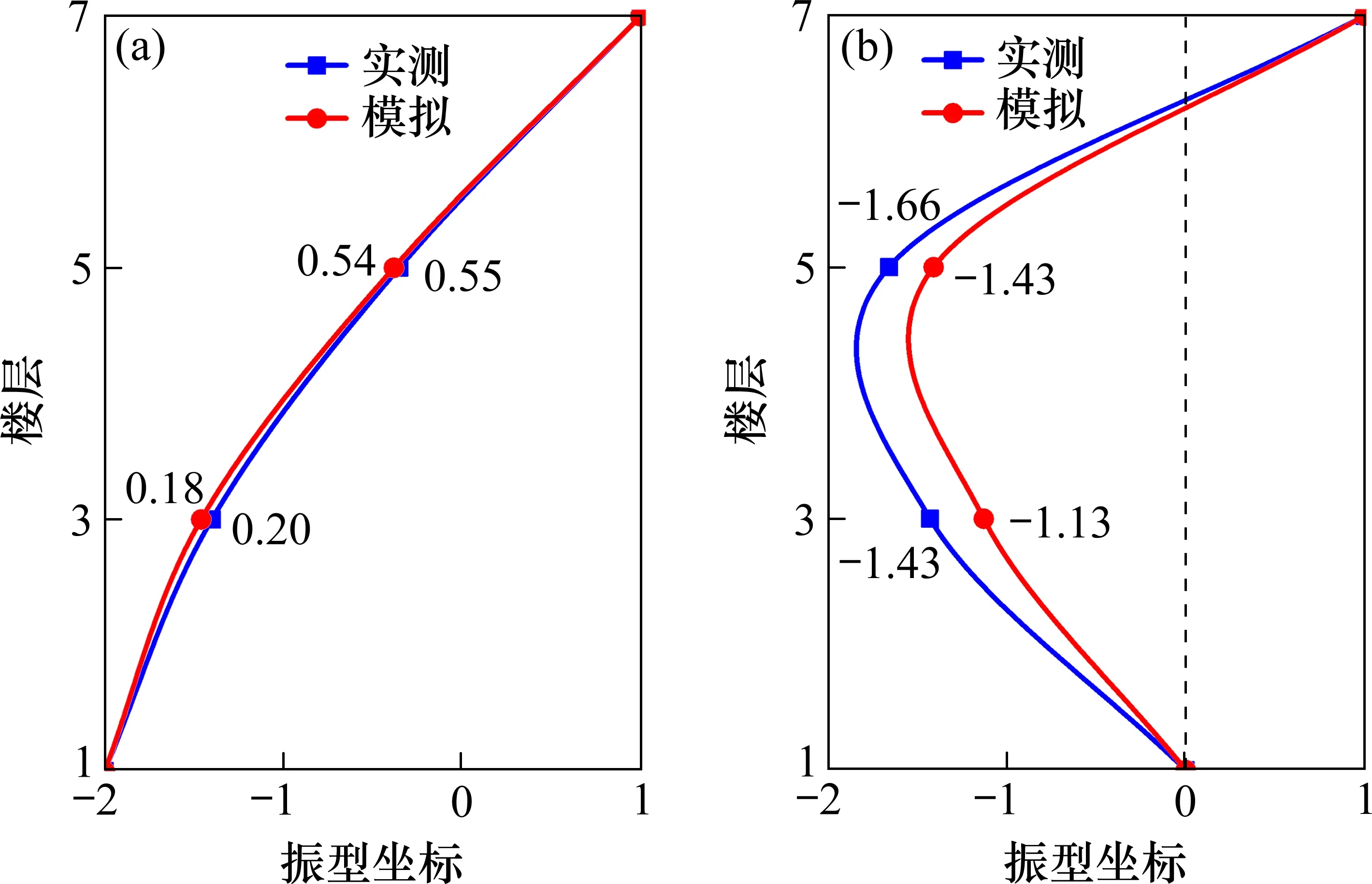
图9 实测和模拟振型对比Fig.9 Comparison of measured and simulated modes

4 古塔振动响应分析

4.1 荷载的输入

以实测得到的某城市地铁2号线造成的地面振动加速度作为荷载。测试所在区段的隧道截面为拱形，埋深12 m，土层分类为软弱土。测试时采用的地铁车型是B 型车，6 节编组，行车方式为单向行车，运行车速60 km/h，记录地铁线路不同水平距离处地面的竖向加速度，截取列车驶过时的时程(图10)。由于古塔结构的尺寸跨度不大，因此采用一致激励输入荷载。动力计算时采用Rayleigh阻尼，振型阻尼比取0.01，求解阻尼系数；取积分步长0.002 s，运用Newmark-β直接积分法计算地铁列车激励下的古塔动力响应。

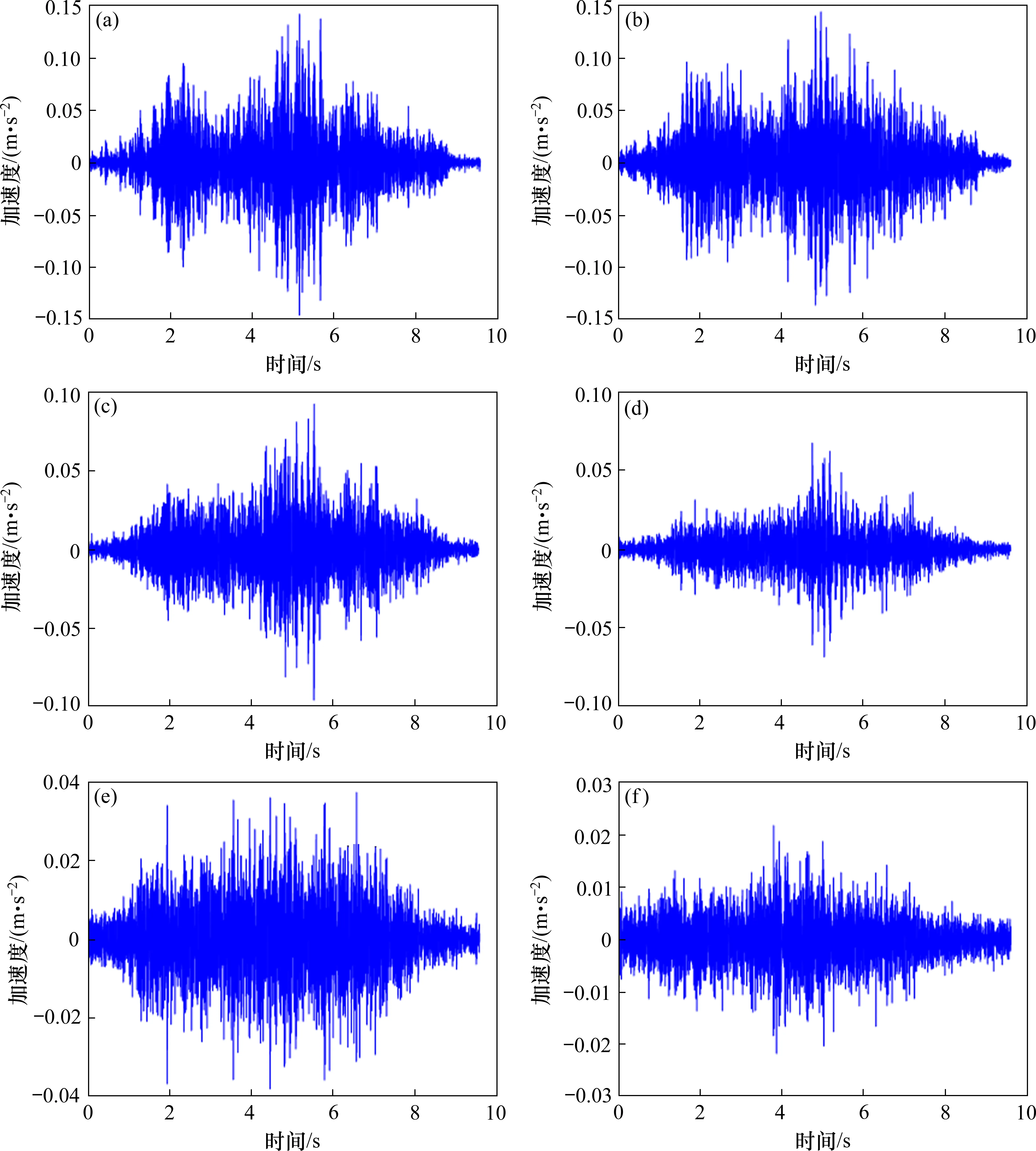
图10 不同振源距离输入的竖向加速度时程Fig.10 Time history of vertical acceleration input under different vibration source distance

4.2 振动响应分析

由于国家规范[12]中对砖石古建筑的评价量为承重结构最高处的水平振动速度(PPV)，故取各楼层最高处为拾振点。

4.2.1 基础工况

取振源水平距离0 m，地基弹模30 MPa 工况为基础工况进行计算。由于在宝塔各层的速度时程和频谱图除幅值外，时程曲线的形式和频谱峰值均无明显变化，故本文只展示顶层的水平振动响应图(图11)。由图11 可知，塔体水平振动的主频为0～15 Hz，低频部分的振动能量较大。

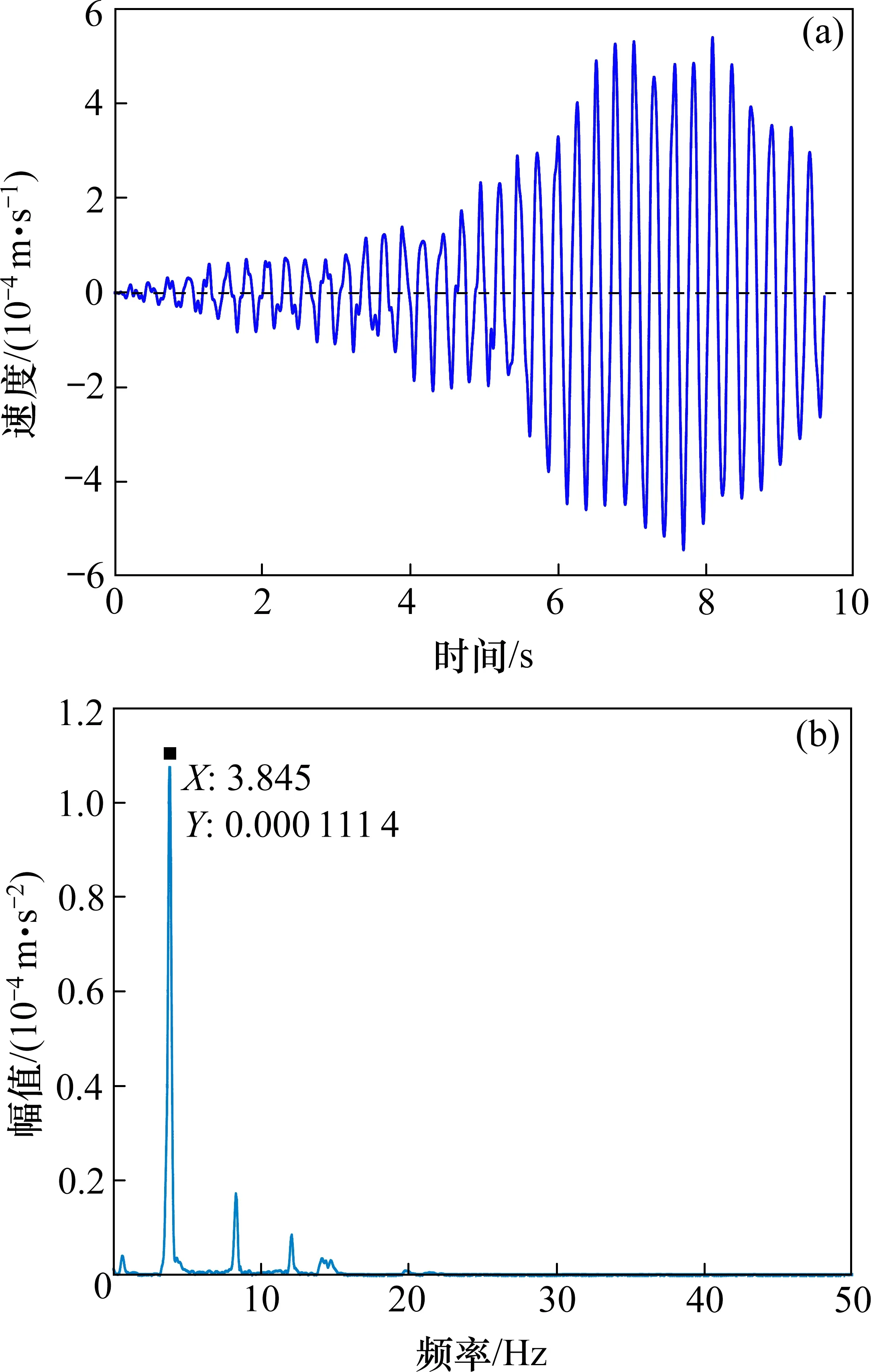
图11 顶层最高处水平振动响应Fig.11 Horizontal vibration response at the highest point of top floor

4.2.2 振源距离的影响

改变振源距离，对其在不同工况下的各楼层最高处水平振动速度进行分析。图12 为改变振源距离所得到的计算结果。

分析图12 可知，所有工况下，水平向振动速度峰值沿宝塔高度方向均呈现先增大后减小再增大的趋势，在顶层达到最大值，表现出鞭梢效应。随着振源水平距离的增加，各层最高处水平振动速度总体呈减小趋势，但当振源距离为25～30 m时存在振动放大现象，这与输入荷载的变化趋势一致。

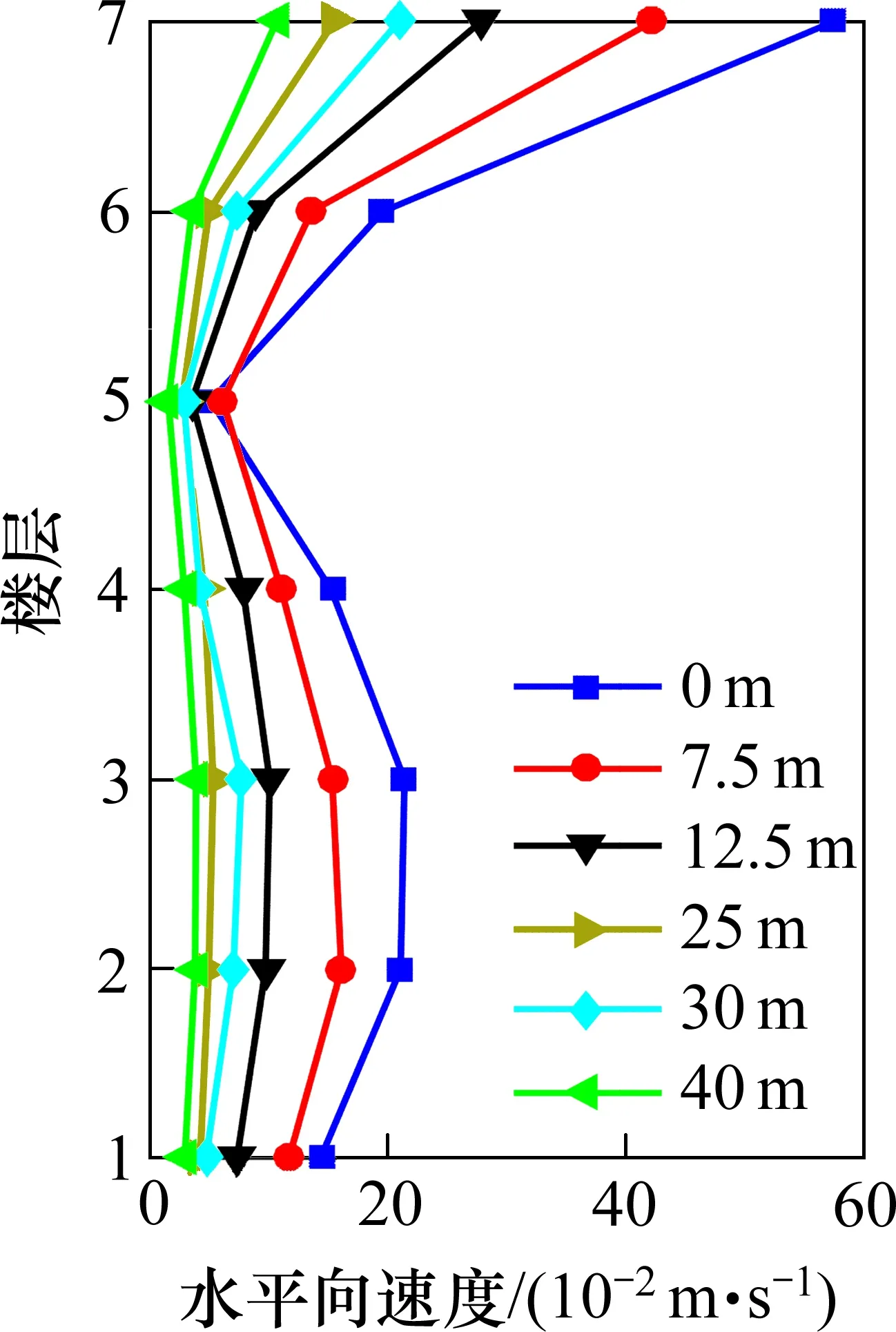
图12 不同振源距离下古塔各层水平振动速度Fig.12 Horizontal vibration velocity of each floor of the pagoda under different distance of vibration source

4.3 古塔安全性讨论

洪山宝塔对应的振动限值为0.36 mm/s[12]。由上文计算结果，当振源距离为12.5 m 时，塔体承重结构最高处水平振动速度为0.278 mm/s，虽然未超过限值，但随后在振动放大区该数值又出现0.05 mm/s 的增幅，这个增量对于古建筑而言较为敏感，尽管振动放大区的顶层水平速度仍未超过省级文物保护单位的振动限值，但由于古建筑保护级别是动态的，类似于上述增幅的变化对古建筑是潜在隐患，故此放大现象也值得关注。

5 结论

1) 动力测试和有限元模拟结果均表明洪山宝塔在东西和南北方向的前2 阶频率接近，且均为平动振型。

2) 地铁列车荷载作用下，洪山宝塔水平振动能量主要集中在低频部分，主频集中在0～15 Hz。

3) 古塔各层最高处水平向振动速度沿塔高度方向均呈现先增大后减小再增大的趋势，在顶层达到最大值。

4) 随着振源水平的增加，古塔各层最高处水平振动速度总体呈减小趋势，但当在一定范围内时存在振动放大现象。由于古建筑对振动速度变化非常敏感，建议在进行地铁线路规划时，尽量避免将古建筑处于振动放大区内。