基于动测法的古塔结构抗震性能检测与评定
2022-08-18王凤华黄襄云王伟明
王凤华, 黄襄云, 王伟明
(1.广东建设职业技术学院,广州 510440;2.广州大学工程抗震研究中心,广州 510405)
0 引言
古塔是我国古代建筑的主要组成部分,是优秀的历史文化遗产,在漫长的历史过程中,古塔历经沧桑,受到了人为和自然的破坏。我国是一个地震频发的多地震国家,拥有许多历史悠久的古塔建筑,这些古塔建筑大多处于地震高发区域。据文献统计,导致古塔破坏和倒塌的原因大部分是由于大地震造成的,如何对古塔进行检测及抗震加固已越来越受人们的重视,一些学者开始着手探讨古塔的动力性能和抗震加固方法,但往往局限于个别古塔的理论及试验分析与探讨上[1-9]。因此,文中提出用动测法测定古塔自身的强度、刚度和动力学特性,对古塔结构在地震中受到的震害进行分析,这是考察古塔抗震能力,对其进行抗震或可靠性鉴定及震害预测的基础,有了这些资料,才能分析古塔在遭遇地震作用时的反应和可能出现的损坏情况,找出古塔结构在地震中容易受到损坏的薄弱环节,对其采用有效的抗震加固措施进行修复和保护,为类似古塔的抗震与可靠性鉴定、震害预测提供了一种新的手段。
1 古塔等砌体结构侧向刚度与轴心抗压强度之间的关系
1.1 古塔的侧向刚度
我国古塔多数为多层砖砌体结构,体形简单且构件单一,根据文献[10],侧向刚度可表示:

式中,H为古塔等砖砌体的高度;E为砌体的弹性模量;G为砌体的剪切模量;ξ为剪切力不均匀系数;A为砖砌体截面积;JZ为惯性矩。
1.2 古塔的弹性模量
古塔等砌体结构轴心受压时应力应变曲线可根据国内外试验资料,砌体轴心受压时σ-ε可用式(2)表示[11]:

式中,αm为刚度与轴心强度的关系系数;α为弹性特征值,据我国176种墙体的试验[11]数据,对砖砌体取αm=463;fm为砌体结构的轴心抗压强度平均值;fu为砌体结构的轴心抗压强度极限值。
1.3 古塔侧向刚度与轴心抗压强度之间的关系
将古塔的割线模量式(3)代入侧向刚度式(1),得到古塔等砌体结构侧向刚度与轴心抗压强度关系如式(4)所示。

2 采用动测法检测及评定古塔结构的抗震性能
2.1 古塔侧向刚度计算公式
古塔等砌体结构可简化为多质点体系的数学计算模型[12],如图1所示。其特征方程:

图1 古塔结构数学计算模型

特征方程中,[K]、[M]分别为剪切型刚度矩阵及主对角线型质量矩阵。
设Ki为古塔结构第i层层间刚度;Mi为古塔第i层层间集中质量;f为古塔基本频率;Ai(i=1,2…,n)为古塔在基本振型下各层的位移,令:

因此,古塔等砌体结构各层墙体的侧向刚度可用式(8)、式(9)计算。
第一层间:

2.2 古塔的侧向刚度及轴心抗压强度
把用动测法测定的古塔的基本频率f和基本振型下各层位移实测值Ai及Mi(i=1,2,…,n)代入用模态识别法求解得古塔各层砌体的侧向刚度式(5)~式(9),得出各层砌体侧向刚度Ki(i=1,2,…,n),从而识别古塔各层间的材料特性,进行古塔的几何特性分析,最后代入式(4)可得各层砌体轴心抗压强度fm,求解古塔各层砌体的轴心抗压强度。
2.3 古塔等砖砌体结构的变形性能
古塔等砌体结构的骨架曲线可用三线型模型表示见图2[13-17],结构变形达到极限位移及临界倒塌时的延性系数分别为μu及μw,如式(10)所示。

图2 三线型模型

式中,Δy为等效屈服位移;Δu为极限位移;Δw为极限位移及临界倒塌(即Vw=0.8Vu)时的位移;Vu为极限荷载。据文献[13]~[17]对97个试件的试验数据进行统计分归类和分析表明,砖墙片的μu及μw值离散性较小,故文中μu及μw取其平均值。
2.4 古塔等砌体结构侧向刚度与等效屈服位移之间的关系
古塔等砌体结构侧向刚度与等效屈服位移之间的关系可表示:

式中,K为该砌体结构侧向刚度;Am为该砌体结构水平截面毛面积;ζ为该砌体结构剪切力分布不均匀系数;α0为K与Δy之间的系数;fv为砖砌体抗剪强度;σ0为层高半高处由墙自重产生的平均压应力。
根据文献[13]~[17]的统计分析,砌体结构墙体α0值离散性较小,因此文中α0值取其平均值。当古塔墙体侧向刚度K利用动测法测定之后,由式(11)可得到等效屈服位移Δy。
2.5 地震作用下古塔结构层间位移分析
根据我国《震害预测工作大纲》及《建筑地震破坏等级划分标准》[(90)建抗字第377号],古塔在基本完好和轻微破坏状态时,属于弹性阶段,可以采用底部剪力法计算各层的水平地震作用力,如式(12)所示:

由各层墙体的侧向刚度式(8)、式(9)和侧向刚度与等效屈服位移之间的关系式(11),可求得古塔各层在弹性阶段下的层间位移:

古塔等多层砌体结构属于多层剪切型结构,根据文献[18],当震害破坏等级为中等破坏、严重破坏和倒塌时,古塔处于弹塑性阶段,其刚度明显降低,地震反应位移增长速率加大。由层间弹性位移乘以弹塑性位移增大系数ηp可得到层间弹塑性位移。
其中层间弹塑性位移增大系数ηp取值与楼层屈服强度系数ξ(i)有关,根据文献[18],文中取屈服强度系数依次为0.5、0.4及0.3,对应预估层间震害等级,分别确定在不同震害破坏等级下的层间弹塑性位移增大系数ηp,如表1所示。

表1 弹塑性位移增大系数
根据古塔各层墙体地震反应位移计算结果及地震破坏等级判别准则,可得到古塔结构各层墙体震害等级,根据古塔各层墙体的震害等级即可综合评估古塔整体的震害等级。
3 实例分析
文中对广州市某古塔进行检测与评定,古塔外形轮廓如图3、图4所示,该塔由主塔和小塔组成,总高度由现地面起计34.246m,古塔为砌体结构[19]。将其根据集中质量法等效为五质点体系的多自由度计算模型,计算简图如图5所示。从塔身抽取砖试件试压,抗压强度测试结果如表2所示。砖砌体表层灰缝材料用砂浆回弹仪进行检测,其回弹值为零,可知砖和砂浆强度都偏低,为计算参数选取的需要,取砂浆强度为最低标号的砂浆-M0.4。

图3 古塔整体外观

图4 古塔外形轮廓

图5 古塔动力计算

表2 古塔抽取砖块试样尺寸及抗压强度测试结果
3.1 测试标准
测试过程和方法按标准进行:JGJ 101-96《建筑抗震试验方法规程》、CECS 74-95《场地微震动测量技术规范》、GB 50011-2001《建筑抗震设计规范》。
3.2 试验手段及测试仪器
试验采用丹麦产4381V型传感器及其配套的电荷放大器见图6。测试时沿古塔结构塔身高度从下至上,沿东南西北四个方向均匀布置10个加速度传感器,传感器布置如图7所示,每一方向测试10次,每次测试约10min。采用DASP信号采集仪记录加速度变化的时程。采用橡胶锤敲击古塔塔身施加冲击力,产生水平向激振,采集古塔产生的微小振动,以识别古塔结构的模态参数。

图6 丹麦产4381V型传感器和放大器

图7 传感器布置示意图
3.3 测试结果
由测试可得古塔各测点的加速度时程,通过自功率谱函数分析可得结构的自振频率和阻尼及结构振型,计算结果见表3,结构第一振型见图8。

表3 古塔自振频率及阻尼

图8 古塔结构第一振型
通过测试得到:
(1) 古塔动力特性:古塔结构的一阶频率为1.25Hz,周期为 0.8s,二阶频率为 2.5Hz,周期为 0.4s,三阶频率为5.5Hz,周期为0.182s,四阶频率为10.3Hz,周期为0.097s。
(2) 结构阻尼比为0.023。
(3) 古塔各测点的加速度时程。
3.4 古塔各质点的侧向刚度和轴心抗压强度计算
用底部剪力法分别计算不同地震烈度下古塔各质点的水平地震力,地震剪力和层间地震反应位移,由弹性模量式(3)及古塔侧向刚度与轴心抗压强度关系式(4)计算古塔各质点的侧向刚度和轴心抗压强度,结果如表4所示。
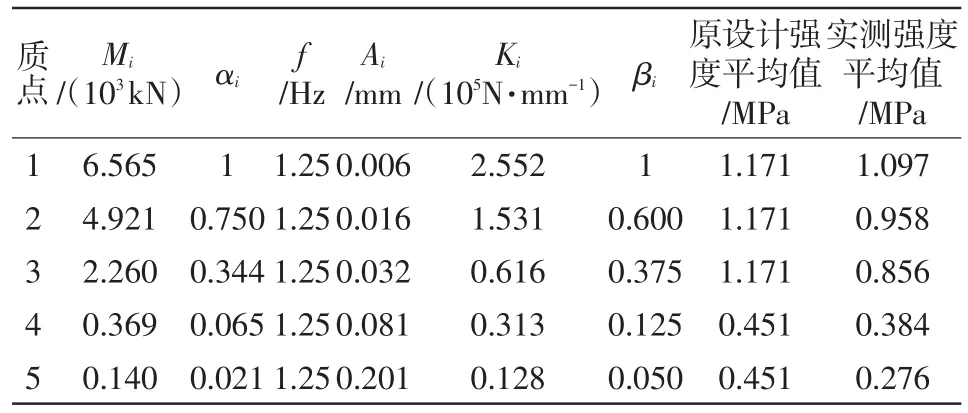
表4 古塔各质点的侧向刚度和轴心抗压强度检测计算结果
3.5 古塔变形性能和震害预测
用底部剪力法计算不同地震烈度下古塔各质点水平地震力,地震剪力和层间地震反应位移,结果如表5所示。由弹性模量式(3)及古塔侧向刚度与轴心抗压强度关系式(4)计算层间等效屈服位移,极限位移和临界倒塌位移,确定震害等级区间,结果如表6所示。比较分析古塔结构各层地震反应位移与变形能力,并根据地震破坏等级判别准则判断各层结构的震害等级,综合评估古塔整体的震害等级,结果如表7所示。

表5 古塔各质点地震反应位移计算结果

表6 古塔各质点震害等级区间
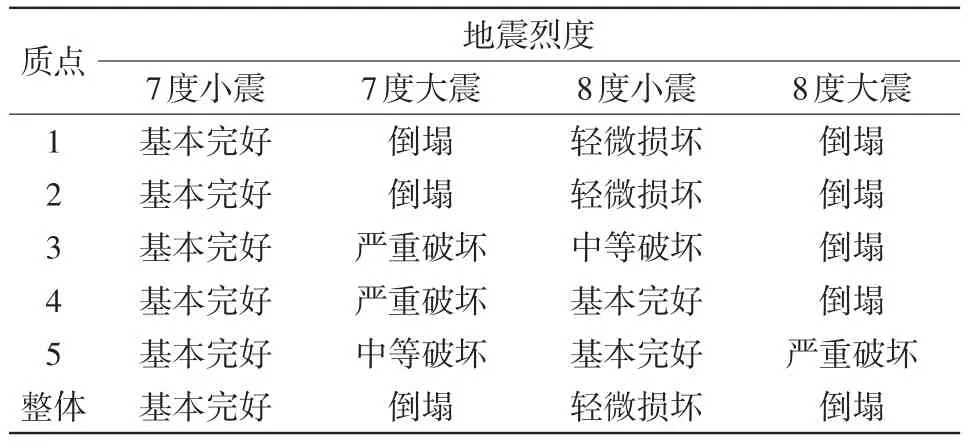
表7 各质点以及古塔整体震害等级评估结果
4 结语
文中提出用动测法对古塔等砌体结构的抗震性能进行评估,并用该方法对广州市某古塔的抗震性能进行实际检测与评定,得出以下结论:
(1) 提出用动测法对古塔等砌体结构的抗震性能进行监测评定,为古塔的强度和质量评估提供了有效的手段。
(2) 采用底部剪力法对古塔进行弹塑性地震分析,找出古塔结构在地震中容易受到损坏的薄弱环节。
(3) 通过计算古塔等砌体结构的层间变形与地震反应位移,根据地震破坏等级判别准则得出古塔各层的震害等级,从而综合评估古塔整体的震害等级,为类似古塔的抗震或可靠性鉴定、震害预测提供了一种新的手段。
