一种配电线路漏电流精确计算方法

周连凯， 张 颖， 伏 睿， 易 庚， 崔 翔， 李彦彦

(1.国网新疆电力有限公司经济技术研究院，新疆 乌鲁木齐 830013； 2.国网新疆电力有限公司， 新疆 乌鲁木齐 830002； 3.西安交通大学 电气工程学院，陕西 西安 710049)

0 引言

配电网的漏电流主要由寄生电容引起，难以精确计算。随着电力电子器件的广泛应用，非线性负荷产生了大量的谐波，特别在线路故障时，产生的漏电流为交直流混合的复杂信号，幅值小，频率高，传统的方均根值计算方法很难进行精确计算[1-2]。为此，国内外学者对此进行了大量研究。文献[3]采用了一种基于FFT的漏电流计算方法，将50 Hz基波分量有效值作为漏电流的有效值。由于该方法需要对漏电流进行频谱分析，当漏电流波形出现畸变时，计算方法不能进行有效的识别和计算[4]。文献[5]将傅里叶变换法和方均根值算法相结合计算漏电流。这种方法具有一定的滤波功能，能够提高计算精度。但由于漏电流是正弦交流、脉动直流与非稳定性信号的混合信号，信号难以完全采样[6]，且傅里叶变换法存在频谱泄漏，该方法的计算准确性难以保证。基于以上原因，本文提出了一种方均根值算法结合全相位傅里叶变换(all phase FFT，apFFT)的漏电流计算方法。该方法首先建立配电线路模型，并进行漏电流计算，将计算值作为本算法的基准值；然后对采集数据进行方均根值计算，并将计算值与基准值进行比较；若计算值小，则进行方均根值计算，以提高计算效率；否则，利用全相位傅里叶变换对漏电流信号进行加窗处理及全相位频谱分析，经滤波得到漏电流的有效值。最后，通过算例，验证了本文方法的准确性与有效性，为漏电流的准确计算提供了一种新的方法。

1 方均根值法

传统漏电流计算主要是方均根值法，其计算式为：

(1)

对(1)式离散化得：

(2)

式(1)、式(2)中I为电流有效值，T为输入信号周期，N为每周期采样点数，Ik为第k点的采样电流值[7]。

由式(2)可知，方均根值法并没有对谐波信号进行处理。当采样信号含有高次谐波时，计算精度会受到影响。

2 全相位傅里叶变换

2.1 全相位傅里叶变换原理

全相位傅里叶变换是由文献[8]最先提出的一种数字图像信号处理方法。该方法的基本原理是：通过对预处理数据进行加权运算，然后再进行傅里叶变换得到全相位傅里叶变换频谱。

设单频复指数信号为：

xn=ej(ω0n+φ)=ej(nβ2π∕N+φ)

(3)

式中：ω0为信号频率。

{x(n)}不加窗的FFT频谱为

k=0,1,…,N-1

(4)

{x(n)}不加窗的apFFT频谱为

(5)

由式(4)、式(5)可知，全相位傅里叶变换频谱幅值为FFT频谱幅值的二次方，即旁谱线相对于主谱线的比值也以二次方关系衰减，使主谱线更突出，因而全相位傅里叶变换具有很好抑制频谱泄漏的性能[9]。

2.2 全相位傅里叶变换与方均根值算法的结合

首先以Simulink中的“RMS”模块计算配电网漏电流并将其作为基准值；然后采集线路漏电流，并根据方均根值法对采集数据进行计算，将计算值与基准值进行比较。若计算值大于基准值，则说明漏电流中谐波、直流分量较高，需要对其进行滤波处理。因此将前一周期的采样点利用全相位傅里叶算法进行计算；若全相位傅里叶算法的计算值小于基准值，则漏电流为全相位傅里叶算法的计算结果。否则进行方均根值计算，漏电流为其计算结果。该算法流程如图1所示。

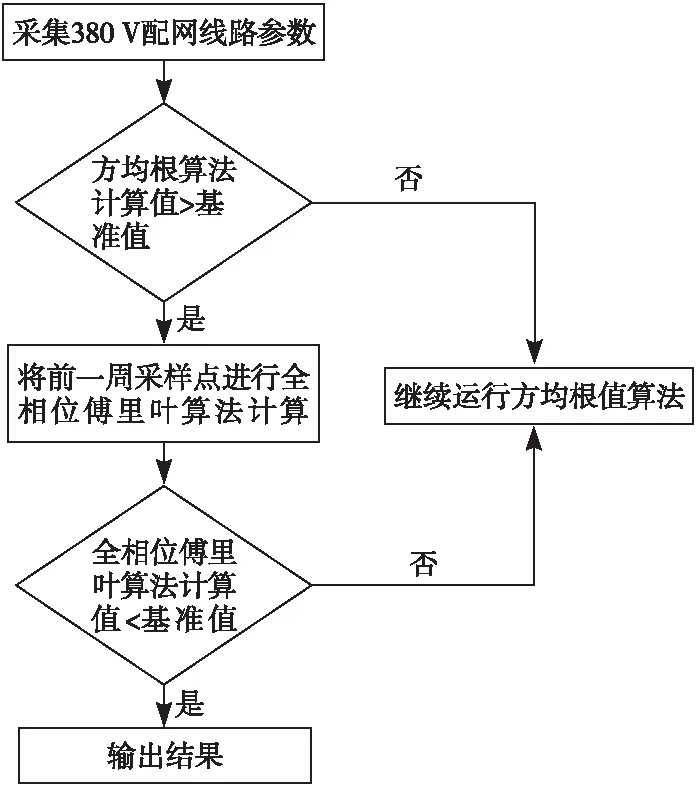
图1 该文算法流程图

3 应用实例

3.1 仿真模型

利用Simulink软件搭建380 V，500 m的配网线路模型如图2所示[5]。

图2 380 V配电网线路模型

设t=0.1 s时线路发生单相短路，同时在电源处加入谐波源，以模拟线路产生的谐波。谐波源为：

i(t)=sinωt+0.1sin3ωt+0.3sin5ωt+0.2sin7ωt

(6)

线路漏电流波形如图3所示。

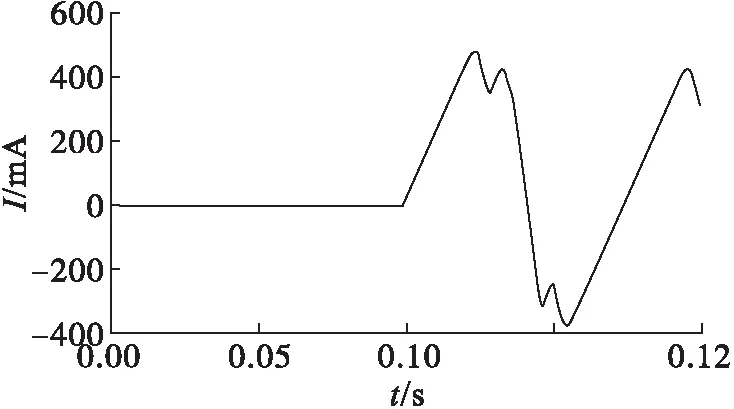
图3 380 V线路漏电流波形

由图3可见，0.1 s之前线路正常运行，漏电流为零；0.1 s之后线路发生故障，漏电流迅速增大至400 mA；漏电流产生了畸变，含有直流分量及高次谐波。

3.2 不同算法下的漏电流计算

3.2.1 方均根值法

漏电流方均根值算法的计算结果如图4所示。

图4 方均根值算法的漏电流波形

由图可见，在谐波影响下，方均根值算法大约在0.7 s后才能计算出漏电流的准确值，计算误差如表1所示。

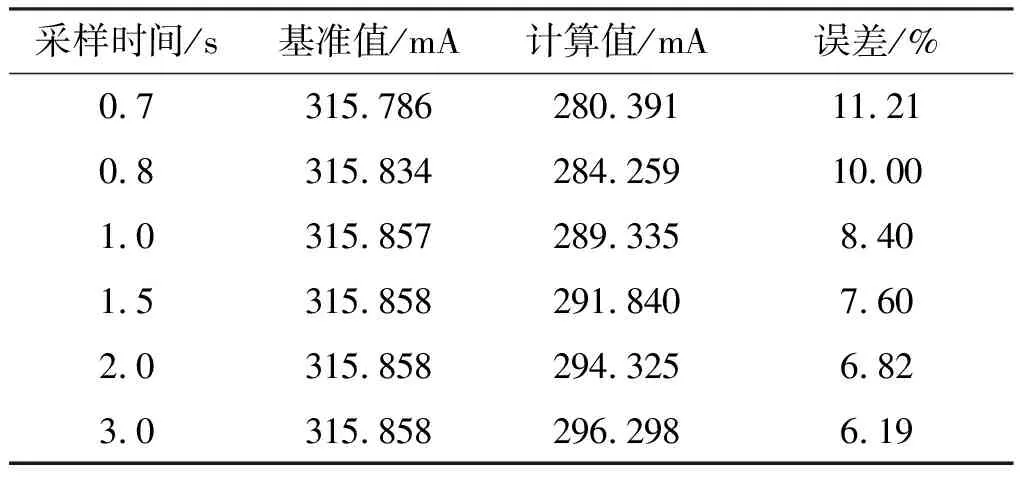
表1 方均根值算法的误差分析

表中：

(7)

式中：基准值为Simulink中的“RMS”模块计算结果。

由表1可知，漏电流方均根值法的计算误差较大。

3.2.2 傅里叶算法

图5为傅里叶算法的漏电流计算结果，计算误差如表2所示。

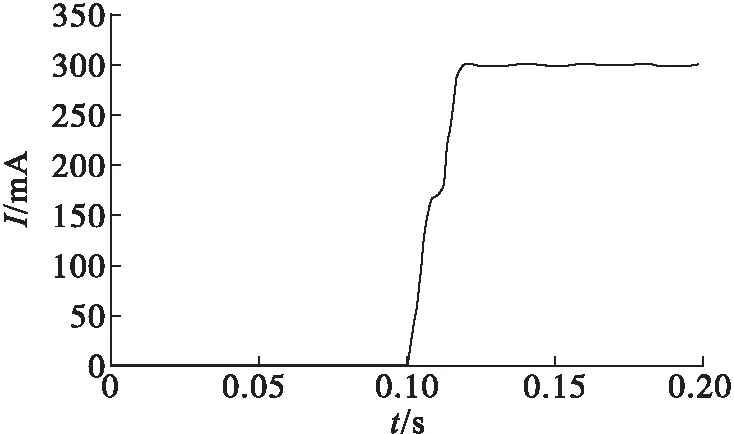
图5 傅里叶算法的漏电流波形

表2 傅里叶算法的误差分析

由图5可见，傅里叶算法仅需一个周波便可准确计算出漏电流值。由表2可知，傅里叶算法的计算精度明显高于方均根值算法。但随着采样时间的增加，由于谐波影响会产生一定的频谱泄露，傅里叶算法的计算误差也在逐渐增大。

3.2.3 结合方均根值法的傅里叶算法[5]

图6为结合方均根值法的傅里叶算法漏电流计算结果，计算误差如表3所示。

图6 结合方均根值法的傅里叶算法漏电流波形

相比于图5，图6的漏电流波形更陡，即可以更快速的计算出漏电流的准确值。

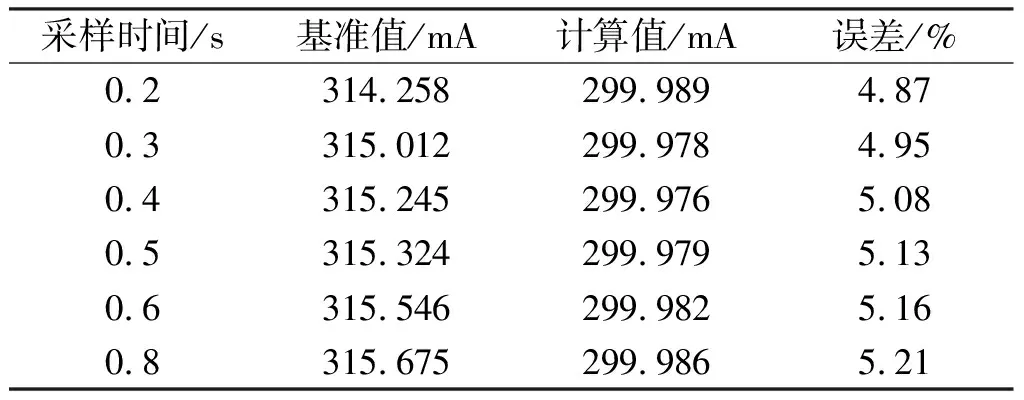
表3 结合方均根值法的傅里叶算法计算误差

由表3可知，将傅里叶算法和方均根值法并不会提高显著计算精度，且其计算误差会随时间的增加而增大。

3.2.4 该文算法

该文的结合全相位傅里叶算法的方均根值算法漏电流计算结果如图7所示，计算误差如表4所示。

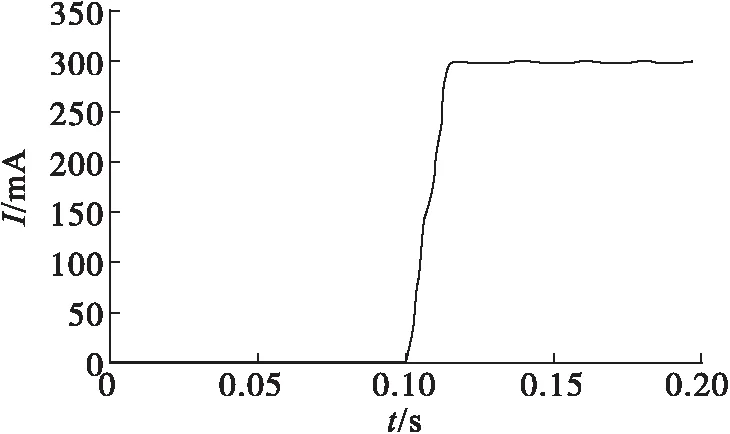
图7 结合方均根值法的全相位傅里叶算法漏电流波形

表4 结合方均根值法的全相位傅里叶算法漏电流计算误差

由表4可以明显看出，结合全相位傅里叶算法的方均根值算法计算精度明显的高于其他算法，且随着采样时间的增加，计算误差不断减小，是一种精确的配电网漏电流计算方法。

4 结论

随着配电网中的谐波越来越大，目前的计算方法效率低、精度差。该文提出的结合全相位傅里叶变换法与方均根值法的漏电流计算方法，结合了方均根值法的简单高效与全相位傅里叶变换法准确性，克服目前计算方法的缺点，计算高效、准确，为配电网漏电流的准确计算提供了一种新的理论方法。