基于PLC技术的海洋自升式平台中控系统自动化控制方法

马振超, 李会通，司江舸

(中海油能源发展股份有限公司工程技术分公司，天津 841000)

0 引言

人们将目标转向资源更为丰富的海洋，让海洋成为继陆地资源后，又一资源开发焦点[1]。原油开发主要采用钻井工程作业的方式，实现原油开采，其相对陆地作业，需要面对海上多变的气候、狭小的作业和生活空间[2]。基于此，相关学者研究出集钻井、动力、通讯、导航、安全救生、作业人员生活设施等设备于一体的海洋自升式平台[3]。海洋自升式平台由三部分组成，需要通过平台的中控系统，控制平台安全、稳定运行[4]。

目前，国内外根据海洋自升式平台作业方式与作业需求[5]，已经研究出定点控位、模型预测控制、轨迹控制、循线控制、跟踪控制、鲁棒控制等中控系统控制海洋自升式平台方法。在国内外研究基础上，相关学者提出如下观点。文献[6]将地质导向钻井平台作为研究对象，根据平台的作业流程，获取平台运行关键参数，依据这些参数，通过机器学习方法实现平台运行轨迹控制。文献[7]将无人平台作为研究对象，依据无人平台的运行特点，将EMS功能应用在无人平台的中控系统中，实现中控系统控制无人平台进行信号采集、远程启停等工作。文献[8]将开环电机的多路激光拉曼光谱仪光路作为研究对象，针对开环电机存在的精度低问题，设计闭环控制算法，控制开环电机，实现多路激光自动化控制。

在自动化控制海洋自升式平台时，位移响应和速度响应减震幅度偏小，导致平台减震控制效果差，为此提出基于PLC技术的海洋自升式平台中控系统自动化控制方法，为海洋油气资源开发提供技术支撑。

1 基于PLC技术的海洋自升式平台中控系统自动化控制方法

海洋自升式平台建立在海平面上，会受到海洋复杂海况的作用，出现如图1所示的六个自由度特征。

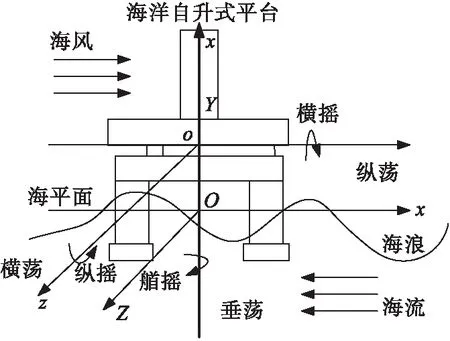
图1 海洋自升式平台六个自由度运动图

从图1中可以看出，平台在海水的推力作用下出现位置缓慢变换的低频分量变化，以及海浪波动下产生的周期性震荡的高频分量[9]。受这两种分量的作用，平台仅会出现横摇、艏摇和纵摇三个自由度的运动。所以，中控系统只需要控制平台的三个自由度，就能减少平台在海洋海况作用下产生的振动。为此，通过建立海洋自升式平台在海洋上的运动数学模型，利用PLC技术，实现海洋自升式平台中控系统自动化控制平台结构振动，保障平台运行的稳定性。

1.1 建立海洋自升式平台运动数学模型

1.1.1 坐标系转换

基于图1所示的海洋自升式平台六个自由度运动图，采用大地坐标系作为海洋坐标系，其原点O为静水平面的任意一点，所建立的坐标系如图1中的O-XYZ所示。

海洋自升式平台坐标系，如图1中的o-xyz所示。由于海洋自升式平台是搭载在船舶上，通过船舶实现钻井工程作业。是以，采用运动坐标系0-xyz表示，其原点位于船舶重心，x，y，z三轴与o-xyz坐标系x，y，z三轴重叠。所以，平台与船舶坐标轴指向方向，均随船体运动的变化而变化。

由于平台位于船舶上，在一个周期内，可以在大地坐标系中，得到船舶状态信息，以此计算船舶位置、速度、控制力等数据时，需要在平行坐标系中进行，再按照计算结果，在大地坐标系中确定平台运动情况。为此，建立大地坐标系与船舶坐标系的转换矩阵。假设，平台在船舶与大地两个坐标系下的位置和速度向量如下：

(1)

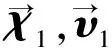
根据式(1)所示的位置、速度向量，可以确定水平面运送平台的位置与速度向量如下：

(2)

基于此，得到的坐标系转换关系δ为：

(3)

式中：R(φ)表示非奇异的坐标转换矩阵[11]。

依据式(3)所示的坐标系转换关系，即可实现船舶、大地两个坐标系的转换。此时，即可建立平台低频运动数学模型，为海洋自升式平台中控系统自动化控制器设计提供依据。

1.1.2 平台低频运动数学模型

通过式(3)，确定的船舶动力定位特性，结合船舶操纵理论，得到的平台非线性运动方程为：

(4)

式中：m表示平台的质量；m′表示附加质量；P表示船体水动力；W表示波浪漂移作用力；F表示海风作用力；L表示海洋洋流作用力；D表示船舶推进器力；G表示转动惯量；G′表示附加转动惯量；N表示力的分布[12]。

为实现不同坐标系下物理量的转换，根据式(4)所示的非线性运动方程，将其转换为线性方程，得到的平台低频运动方程为：

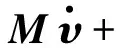
(5)

式中：M表示质量矩阵；ϑ表示阻尼矩阵；F1表示海洋环境作用力；F2表示船舶有效推力器产生的运动自由度力矩。

式(5)即为此次研究建立的平台低频运动数学模型。根据式(5)所示的运动数学模型，采用PLC技术设计自动化控制器和控制算法，实现中控系统自动化控制海洋自升式平台。

1.2 中控系统自动化控制海洋自升式平台

依据式(5)所示的运动数学模型，选择基于ARM的PLC的单元式PLC作为中控系统控制器。单元式PLC由基本单元、扩展模块、特殊模块三部分组成，具有完整的PLC硬件平台，且可以拓展PID控制程序，通过PLC实现PID控制。

基于此，根据式(5)所示的平台运动模型，在单元式PLC扩展模块上，应用DA转换PID与模糊控制器控制输出接口，在平台中控系统中，增加自动化控制功能。因此，设置出如图2所示的自动化控制器。

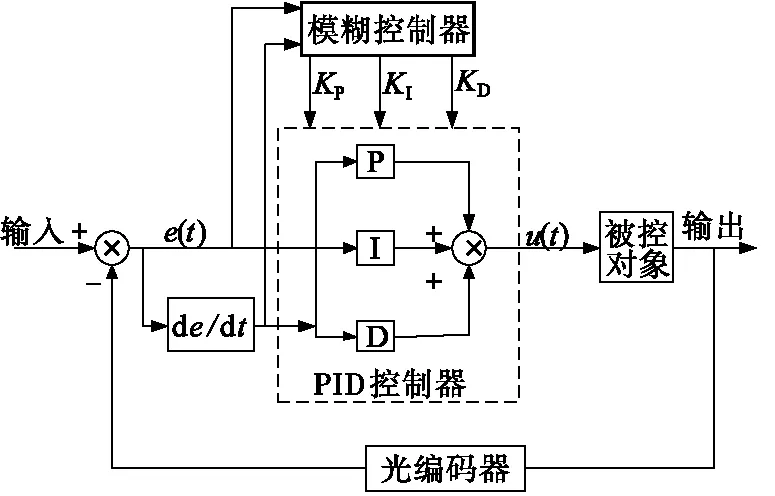
图2 自动化控制器

图2中，u(t)表示控制量；e(t)表示控制反馈值与设定值之间产生的偏差；K表示系数[13]。

根据图2所示的控制器，在PLC的可编程单元中，编写中控系统自动化控制算法中的连续控制过程，如下式所示：

(6)

式中：U(t)表示控制器输出控制值；n表示中控系统采集平台运动样本序号；T表示中控系统采样周期；i=1,2,…,n表示第i次采样[14]。

根据式(6)，得到中控系统n-1次采样时刻的输出值U(n-1)：

U(n-1)=

(7)

将式(7)与式(6)作减法处理，得到的控制器自动化控制算法，如下式所示：

ΔU(n)=U(n)-U(n-1)

(8)

式(8)即为单元式PLC可编程单元中编写的自动化控制算法[15]。

将式(8)所示的控制算法，以及图2所示的控制器，分别编写、接入单元式PLC可编程单元与扩展模块中，就可实现海洋自升式平台中控系统自动化控制。

2 数值算例

选择基于冗余技术的控制方法和基于闭环控制的控制方法作为此次实验的对比方法，将某海域某海洋自升式平台作为数值模拟对象，验证此次研究的基于PLC技术的海洋自升式平台中控系统自动化控制方法。

2.1 设置海洋自升式平台仿真数值

此次实验选择的海洋自升式平台由桩腿、主船体、升降机构、平台结构组成，整个平台的高度为160 m，总质量为9185.4吨，其在海洋上的作业参数，如表1所示。

按照表1所示的平台作业参数，仿真的海洋自升式平台三维模型，如图3所示。

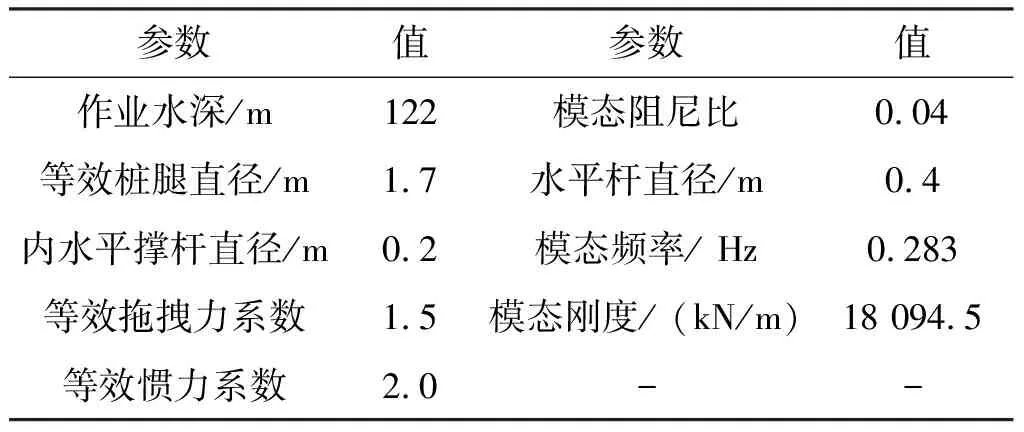
表1 平台作业参数

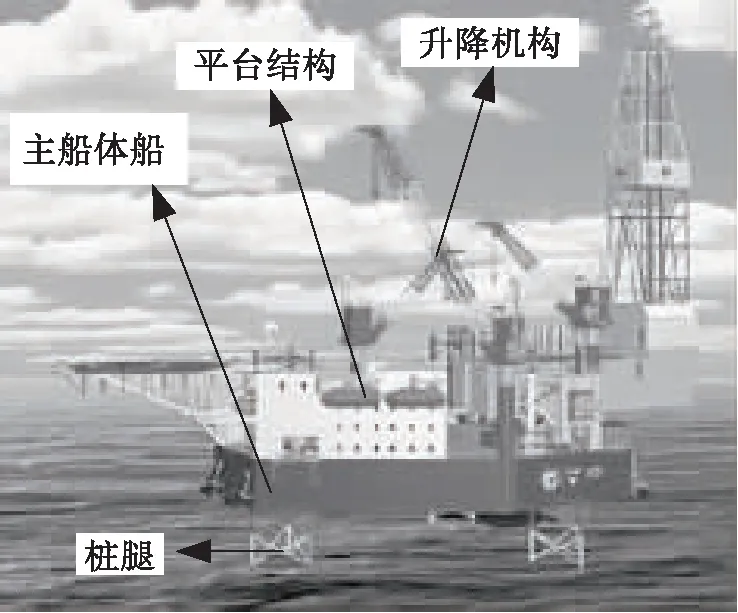
图3 平台三维模型图

2.2 海况参数设置

依据该实验选择的某海域平台，将该海域参数作为此次实验海况参数。为此，选择JONSWAP谱作为海洋海浪谱，将海洋的有义波高设置为10 m，峰值周期设置为8 m。

2.3 控制性能分析

在此次实验设置的海况条件下，采用此次选择的三组控制方法，自动化控制中控系统控制平台结构，每种方法在该实验设置的海况下的仿真时长为300 s。测定三组方法控制平台结构后，平台在300 s时间内，位移和速度数据变化情况，并将控制后的结果与控制前的结果进行对比，通过比较三组方法控制平台结构位移和速度响应均方差，验证研究方法的控制平台减震效果。

2.3.1 位移和加速度数据变化

2.3.1.1 位移

平台位移数据变化，如图4所示。

从图4中可以看出，基于冗余技术的控制方法的位移响应波动幅度均值为0.025 1；基于闭环控制的控制方法的位移响应波动幅度均值为0.034 6；研究方法的位移响应波动幅度均值为0.014 8。可见，研究方法控制平台后，平台位移变化极其微小，其产生的振动影响基本可以忽略不计。

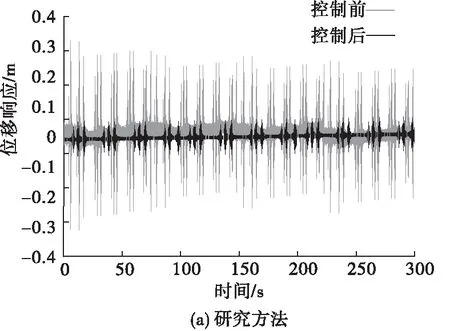
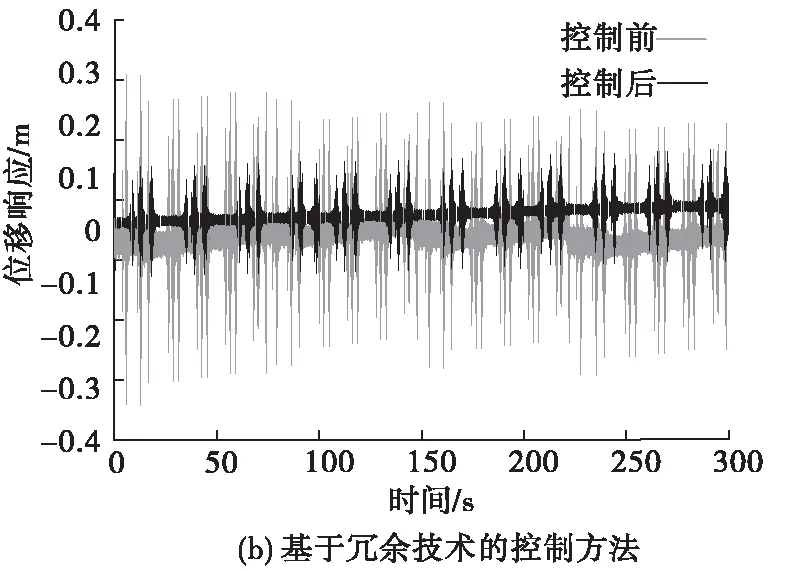
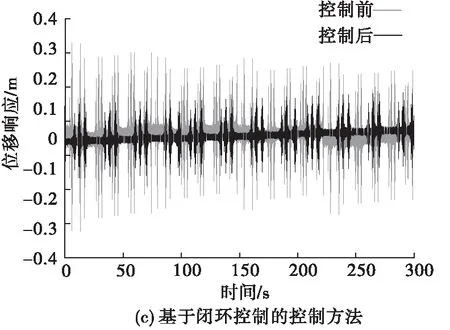
图4 位移数据变化图

2.3.1.2 速度

平台速度数据变化，如图5所示。可以看出，基于冗余技术的控制方法和基于闭环控制的控制方法的速度响应波动幅度均在[-2，+2]之间，产生的速度响应波动幅度较大；研究方法的速度响应波动幅度在[-0.05，+0.05] 之间，速度响应波动幅度极小。可见，研究方法控制平台后，平台产生的速度变化可以忽略不计。

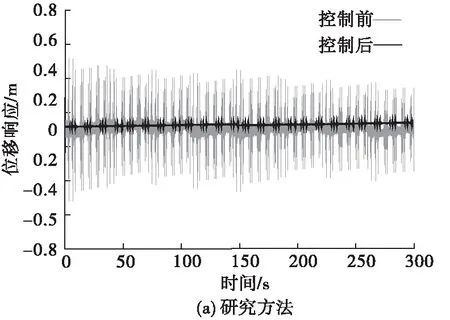
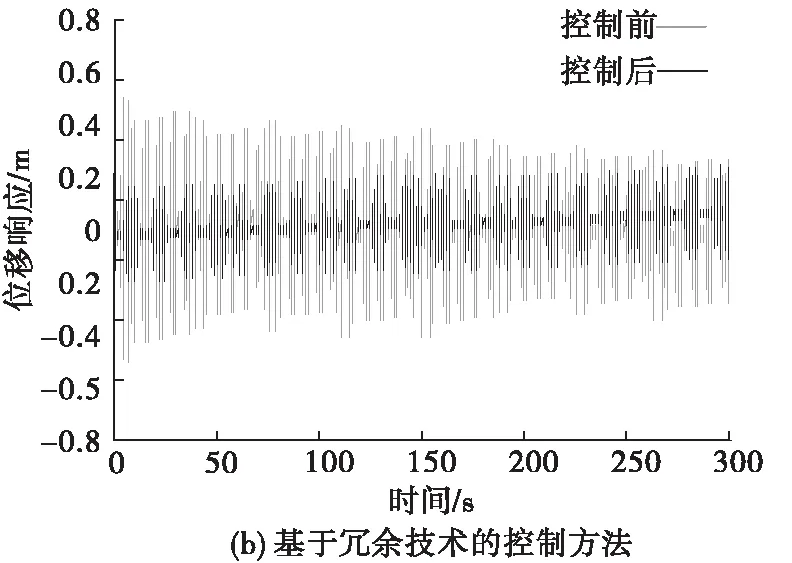
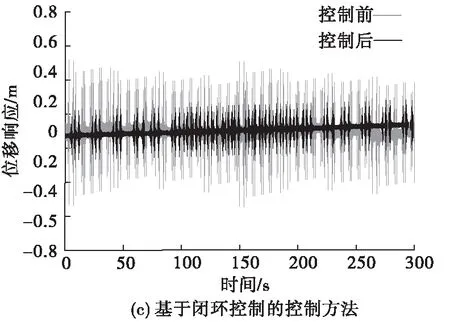
图5 速度数据变化图

2.3.2 减震控制效果对比

基于图4和图5得到的三组控制方法，控制平台结构位移和速度数据，采用下式所示的均方差计算公式，计算三组方法控制平台结构的减震幅值，其计算结果如图6所示。

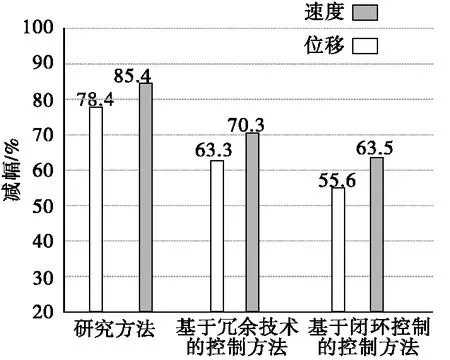
图6 减震幅值对比图

(9)

式中:E表示均方差；ω表示波的圆频率；x表示位移；υ表示速度；d表示微分算子；Sx表示位移波的能量和；Sυ表示速度波的能量和。

从(9)式中可以看出，E值越大，控制方法控制平台的减震幅度越高，方法的控制性能越优。

从图6中可以看出，研究方法的位移响应减震幅值，相较基于冗余技术的控制方法和基于闭环控制的控制方法分别高15.1%和22.8%；速度响应减震幅值分别高15.1%和21.9%。可见，该研究方法具有较优的减震控制效果。

3 结束语

该研究选择具有扩展与编程功能的PLC，设计中央控制系统控制器和控制算法，促使中央控制系统具有自动化控制性能。但是该研究未曾考虑控制方法的时滞现象，且在实际应用过程中，难以满足动力和几何相似准则。因此在今后的研究中，还需深入研究新的试验方法和控制方法时滞现象的解决方法，进一步增强方法的控制性能。