具有恐惧效应和时滞的捕食模型的稳定性分析
2022-04-12刘白茹刘俊利
刘白茹, 刘俊利, 吕 潘
(西安工程大学 理学院, 陕西 西安 710600)
捕食者-食饵的相互作用是自然界生态群落的一个重要特征,利用数学模型研究恐惧因子对捕食者-食饵模型的影响已经成为生态学和理论生物学研究的一个重要领域。在捕食者-食饵的相互作用中,捕食者可以通过直接捕食来影响食饵种群[1],然而捕食者的存在可能会显著地改变食饵的行为和生理机能,以至于它可能比直接捕食更有效地影响食饵数量[2-3],许多食饵物种由于害怕捕食风险而改变其行为,并表现出多种反捕食反应,如觅食活动、栖息地改变、警惕性提高和一些生理变化等[4-5]。Wang等[6]首先提出了一种带有恐惧效应捕食-食饵模型,数学分析表明,强烈的恐惧可以通过排除周期解的存在性来稳定捕食系统,而相对较弱的恐惧可以通过次临界Hopf分岔产生多个极限环。Mondal等[7]研究了捕食者-食饵模型的动态行为,该模型结合了恐惧和额外食物的影响,研究了不同平衡点的稳定性和Hopf分岔的存在性。Pal等[8]讨论了一类带有恐惧因子且遵循Beddington-DeAngelis功能反应的捕食者-食饵模型,并分析了模型的持久性、稳定性和分岔。文献[6-8]考虑了不同功能反应下的捕食者-食饵模型中的恐惧效应对模型的影响,得到恐惧会影响食饵种群的出生率的结论。然而捕食者也可能通过改变食饵与其他物种的相互作用来改变食饵的种群动态。因此,对物种共存的影响不仅取决于捕食,还取决于种间竞争[9]。另外,时滞作为种群生态学中的一个关键因素,几乎存在于物种生长以及种间相互作用的每个环节[10-12]。Wang等[13]提出了一个具有恐惧代价和适应躲避捕食者代价的捕食-食饵模型,该模型将食饵分为幼年和成年两个阶段,通过数学分析得到当时滞处于中间值时,正平衡点可能失去稳定性,当时滞较大时,正平衡点可能重获稳定。秦丽等[14]研究了一类具有双时滞和阶段年龄结构的三维捕食模型,选取时滞作为分岔参数,从理论上对时滞模型的正平衡态进行了稳定性分析,得出捕食者会随着时滞的增加而灭亡。
在以上文献的基础上,本文考虑了食饵具有竞争者,并将捕食者捕获食饵转化为其自身生物量的时滞与恐惧效应相结合,研究一个时滞微分方程模型。
1 模型的建立
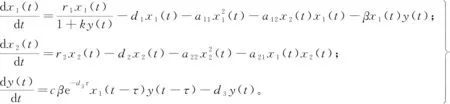
(1)
式中:x1(t)、x2(t)、y(t)分别表示食饵、食饵的同类竞争者(下文简称竞争者)和捕食者在t时刻的密度;r1、r2分别表示食饵和竞争者的出生率;d1、d2、d3分别为食饵、竞争者和捕食者的死亡率;a11为食饵种内竞争导致的衰减率;a22为竞争者种内竞争导致的衰减率;a12为竞争者对食饵竞争资源导致的衰减率;a21为食饵对竞争者竞争资源导致的衰减率;c为捕食者捕食食饵后转化为自身生物量的转化率,c∈(0,1);τ为食饵被捕食者捕食后转化为捕食者自身营养所需要的时滞;k、τ为非负常数,其余参数为正常数。
根据模型的生物学意义,假设捕食者只捕食食饵x1、r1>d1,r2>d2且a11a22≠a12a21。
模型(1)的初始条件为

(2)

下面给出模型解的非负性和有界性。
定理1 在初始条件(2)下,系统(1)的解是非负的。
证明 将模型(1)表示成向量形式,令
X=(x1,x2,y)T∈3,

(3)
式中F:C+→3且F∈C∞(3),则式(3)变为
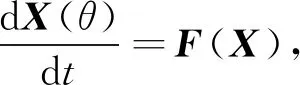
(4)

定理2 对于满足初始条件(2)的模型(1)的任意解,都存在一个正数M>0和T>0,使得当t≥T时,有x1(t)≤M,x2(t)≤M,y(t)≤M。
证明 先考虑系统

令L(t)=ce-d3τx1(t-τ)+x2(t)+y(t),则当t>t1+τ时,有
由此得
因此x1(t),x2(t),y(t)有界。
2 平衡点的存在性和局部稳定性
首先求模型(1)的平衡点。令模型(1)右边的表达式等于零,计算得:
1) 模型(1)总存在种群灭绝平衡点E0=(0,0,0)。
2) 当r1>d1时,模型(1)存在只有食饵的平衡点
当r2>d2时,模型(1)存在只有竞争者的平衡点
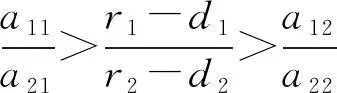


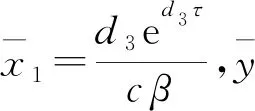

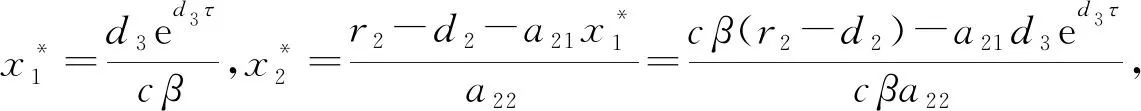

下面对各个平衡点的稳定性进行分析。
定理3 平衡点E0总是不稳定的。
证明 对于平衡点E0,它的特征方程为
(λ-r1+d1)(λ-r2+d2)(λ+d3)=0。
显然,上式有2个正特征根为λ1=r1-d1>0,λ2=r2-d2>0;一个负特征根λ3=-d3<0。因此平衡点E0不稳定。
定理4 关于平衡点E11,E12,E13的稳定性有以下结论:
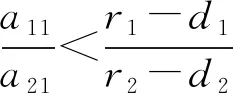
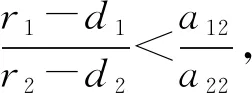
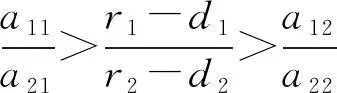
证明 1) 对于平衡点E11,它的特征方程为

(5)
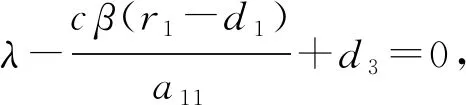
将实部与虚部分离并整理得到
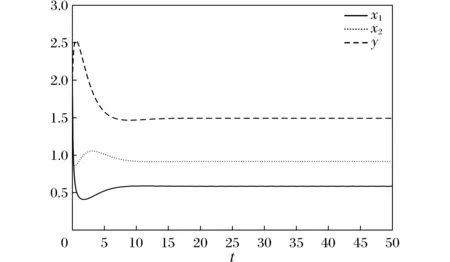
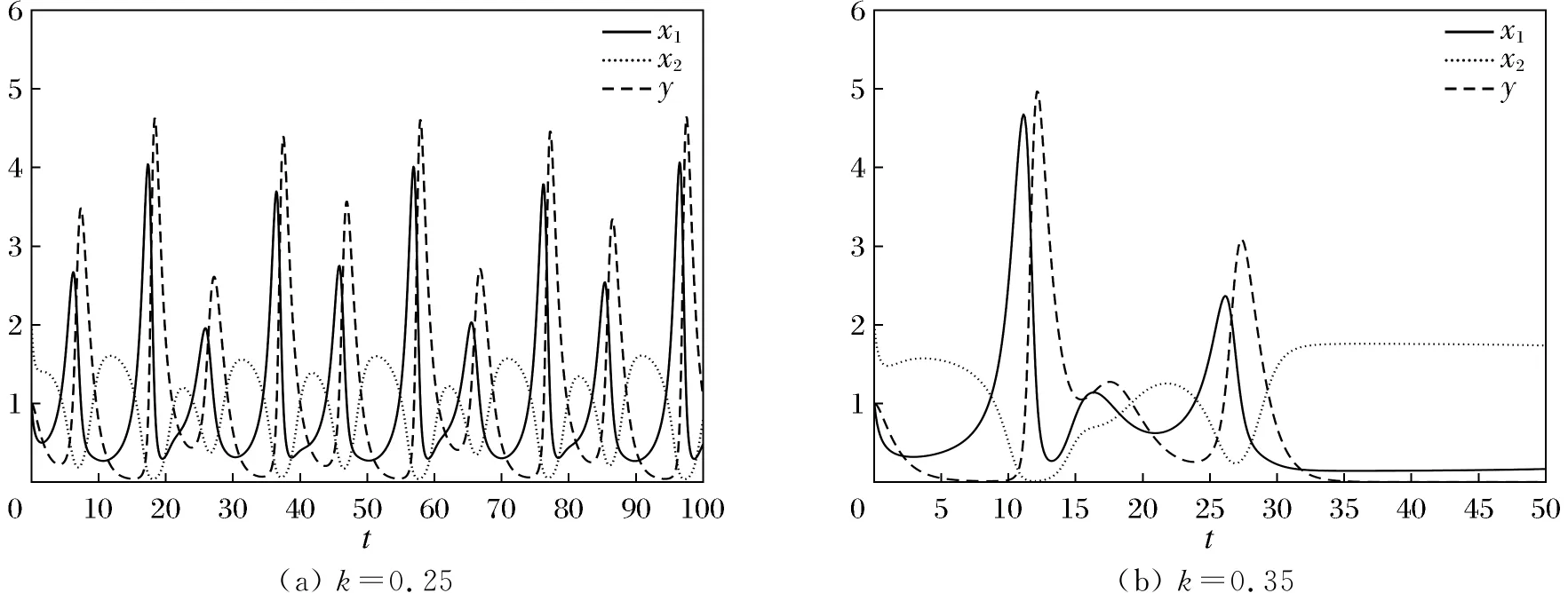
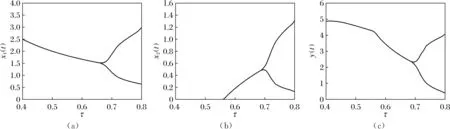
则当cβ(r1-d1)e-d3τ 2) 平衡点E12处的特征方程为 3) 平衡点E13处的特征方程为 (6) ⅰ) 当m2-m4≥0时,无竞争者平衡点E14是局部渐近稳定的,∀τ≥0; ⅱ) 当m2-m4<0时,当τ从零增加时,E14可能失去稳定性。 式中m2,m4在定理证明中得出。 λ2+m1λ+m2+e-λτ(m3λ+m4)=0, (7) 当τ=0时,式(7)变为 λ2+(m1+m3)λ+m2+m4=0, (8) 整理得 (9) 是方程(9)唯一的正根。 因此定理成立。 ⅰ) 当n3-n6≥0时,对∀τ≥0,正平衡点E*是局部渐近稳定的; ⅱ) 当n3-n6<0时,当τ从零增加时,E*可能失去稳定性。 其中,n3、n6在证明中给出。 λ3+n1λ2+n2λ+n3+e-λτ(n4λ2+n5λ+n6)=0, (10) 式中: 当τ=0时,式(10)变为 λ3+(n1+n4)λ2+(n2+n5)λ+(n3+n6)=0, (11) 式中: 因此,由Routh-Hurwitz判据[16]知,特征方程(11)的所有根均具有负实部。 当τ>0时,令λ=iρ,ρ∈+,代入式(10)并分离实部与虚部得到 (12) 整理得 因此定理成立。 分析平衡点的全局稳定性以及无竞争者平衡点E14和正平衡点E*处的分支情况。 引理7[17]考虑下面时滞微分方程 式中a,b,τ>0,当t∈[-τ,0]时x(t)>0,则有 首先讨论平衡点E11的全局稳定性。 (14) 现在讨论平衡点E12的全局稳定性。 下面讨论平衡点E13的全局稳定性。 证明 由方程组(8)可知,ω0对应的τn为 (15) 下面验证横截条件 对式(7)的左右两端同时求导, 因此 则 (16) 下面验证横截条件 对式(10)的左右两端同时求导, 则 为了研究时滞和恐惧效应在模型(1)中的作用,将通过一些数值模拟,来说明前面分析观察到的结果。 选择一组参数: 根据式(17)中的参数值,计算得 满足定理6的全部条件,因此,模型(1)在点E*处是局部渐近稳定的。图1表明了模型(1)在正平衡点E*=(0.525 6,0.974 4,1.687)处是稳定的。 图1 模型(1)在正平衡点处的稳定性 选择另一组参数: 图2(a)中所有参数值同式(18),图2(b)中k=0.35,其余参数值同式(18)。由图2可知,较小的恐惧因子使系统呈现周期性振荡,系统不稳定,当恐惧因子逐渐变大时,由于习惯,恐惧效应不再对食饵产生显著影响,系统开始趋于稳定。 图2 恐惧因子不同时,食饵,竞争者和捕食者种群稳定性的变化 图3表示了当食饵的转化率不同时,模型(1)稳定性的变化,图3(a)中c=0.3,图3(b)中c=0.8,其余参数值同式(18)。由图3可知,当食饵转化为捕食者的转化率较小时,系统趋于稳定,转化率增大,捕食者的数量增加,使得食饵的数量减少,竞争者数量增加,系统变得不稳定,出现周期性振荡。 图3 食饵转化率不同时,食饵、竞争者和捕食者种群稳定性的变化 图4中取初始值为(1,2,1),除变量τ以及a11=1.2之外,其他参数与式(18)中的参数相同。通过数值计算得到:当τ=0.661时,模型(1)在正平衡点E*=(1.492,0.488,2.351)处发生Hopf分支;当τ<0.661时,模型(1)是稳定的,食饵与捕食者随着时滞的增大而减少,竞争者的数量在增长;当τ>0.661,随着捕食者捕食食饵后转化为自身营养所需要的时滞增加,食饵,竞争者及捕食者种群从稳定状态变为周期性振荡。 图4 模型(1)的食饵、竞争者和捕食者关于时滞τ的关系 图5中取初始值为(1,2,1),除变量k之外,其他参数与式(18)中的参数相同。通过数值模拟得到:当k∈(0,0.34)时,模型(1)是不稳定的,食饵、竞争者和捕食者的数量呈周期性变化,随着恐惧因子的增加,当k≥0.34时,模型(1)变得稳定,且食饵和捕食者种群数量随着k的增大而减少。 图5 模型(1)的食饵、竞争者和捕食者关于恐惧因子k的关系 本文研究了一类具有恐惧因素、时滞因素且食饵具有竞争者的捕食者-食饵模型。分析了模型解的非负有界性、平衡点的稳定性、Hopf分支以及数值模拟,说明了不同参数值对系统的稳定性的影响。结果表明随着时滞逐渐增大,模型(1)原本的稳定性被破坏,且在正平衡点E*处发生Hopf分支。而恐惧因子对模型的影响与时滞相反,当恐惧因子逐渐变大,模型(1)由不稳定的状态逐渐变得稳定。从生物学角度上,捕食者在对食饵产生一定程度的恐惧后,由于习惯,恐惧效应在长期内不再会影响食饵种群。因此,时滞和恐惧效应显著影响系统的动态,对生态系统的稳定性起着重要的作用。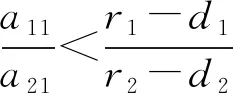



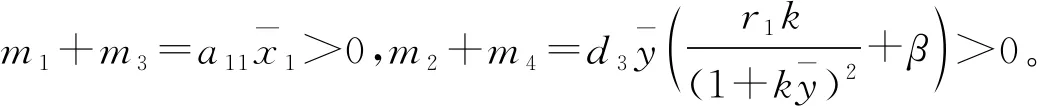

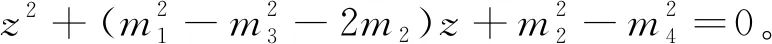
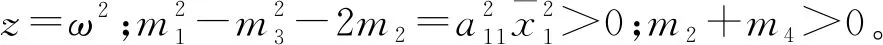



3 平衡点的全局稳定性和Hopf分岔
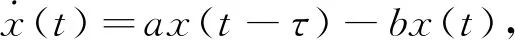
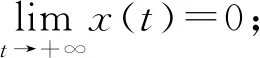

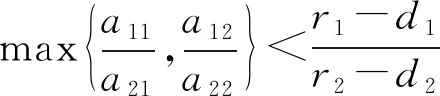
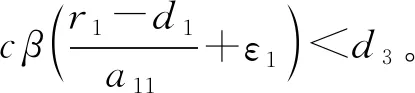
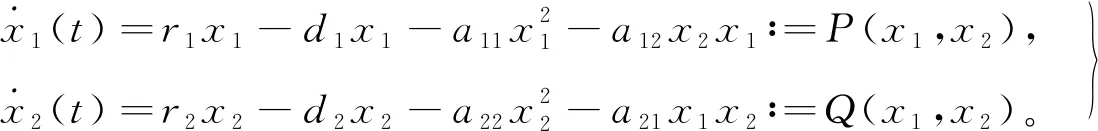
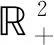
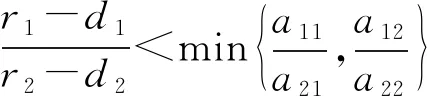
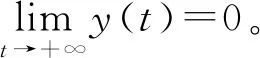
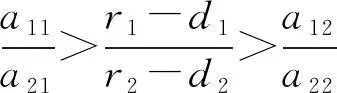



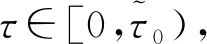
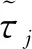
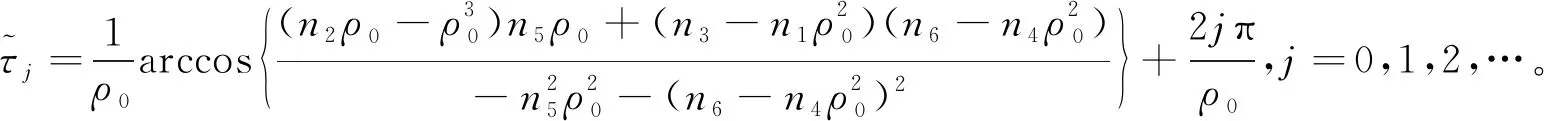

4 数值模拟


5 结 语
