钢铁生产中吊机与多阶段生产协调调度的问题

谢 谢, 郑勇跃, 刘 柳, 李晓丽

(1. 沈阳大学 a. 装备制造综合自动化重点实验室, b. 信息工程学院, 辽宁 沈阳 110044; 2. 辽宁省检验检测认证中心 事业发展中心, 辽宁 沈阳 110032; 3. 吉林省双辽市职业高级中学, 吉林 双辽 136400)

钢铁生产需要经过炼铁、炼钢、精炼、连铸等过程。废钢经由高炉铁水的加工过程变成铁水,经由吊机吊至转炉进行炼钢,炼成的钢水再由吊机吊至精炼炉进一步提纯,精炼结束后再由吊机吊至连铸机上进行连铸加工,连铸结束后经由吊机进行热轧或冷轧等轧制过程。在每个环节中都有多台加工设备,各环节由吊机进行衔接。吊机是钢铁生产企业中必不可少的运输设备,几乎每个关键生产阶段加工工序的过程都由它衔接。这种吊机频繁参与生产的加工模式在装备制造业中越来越普遍,驱动着生产者为适应个性化定制生产模式努力实现柔性生产。由于吊机是各阶段生产之间必不可少的衔接设备,而每个生产阶段都有多台相同的加工工具,因此,我们将m台机器流水车间调度问题进行扩展,将问题扩展为带有吊机运输的流水车间作业的吊机与多阶段生产协调调度问题,目标函数是被加工工件的最小化最大完工时间。

随着生产与吊机衔接制造过程的大规模应用,这种多阶段且生产与运输衔接的柔性制造方式正逐渐取代传统的制造车间,相应的优化技术也成为当前的研究热点。传统的单一生产调度已经不能满足客户的大规模个性化需求,随着吊机这样的大型运输设备的广泛使用,企业迫切需要设计新的优化方法以降低生产成本、缩短制造周期以提高市场竞争力。本文研究的问题以钢铁企业生产过程中吊机参与总流程为背景,提炼出一类吊机与多阶段生产协调调度问题。

如果仅对吊机调度问题进行研究,Philips等[1]提出了电镀生产线的抓钩(hoist scheduling problem)调度,这是关于吊机调度最早的研究。另外两处频繁使用吊机的场景为港口码头的岸边吊机[2](quay crane scheduling problem)和集装箱存储区域的场地吊机(yard crane scheduling problem)。Sun等[3]研究了集装箱终端的岸吊调度,通过分析工作量的分配结构建立了一个新数学模型,并且提出了一个简单的处理吊机不交叉约束的方法。所提出的数学模型基于逻辑的Benders分解,将问题分解为工作量分配的主问题以及操作顺序的子问题,这种基于逻辑的分解保证了算法的收敛,计算结果表明所提出算法的有效性。Kress等[4]考虑了同一跨上2台吊机可中断的集装箱运输过程,也就是允许一台吊机将某一集装箱放置在中转存储区域,再由另一台吊机运输到它的目标位置。比起经典算法,该算法在缩短最大完工时间上是有效的,他们提出了一个动态规划算法以及一个相关的定向搜索算法,动态规划算法使用了定界技术并应用了最优解的统治性质。计算实验证明了动态规划算法的性能超过CPLEX可以快速求解问题的实例。定向搜索算法能够快速地改进已有文献提出的启发式算法的解。文献[5-8]研究了关于集装箱码头的多吊机调度最新的问题及算法,以及吊机在三维空间上的拣选操作。

在钢铁企业中,由于被吊的是高温液态物件,具有温降等特征,因此钢铁企业吊机调度问题相对复杂、研究结果比较少,已有的研究主要集中于某个生产环节中。有关冷轧等需要吊机反复参与的过程,Zapfel等[9]首次研究了钢卷仓库中存、取钢卷的单吊机调度问题。他们将吊机调度看作经典车间调度并建立了一个非线性规划模型,提出基于局部搜索的启发式算法,并通过计算实验测试了算法的性能。Tang等[10]对优化板坯及板卷倒垛和存取顺序的吊机调度进行研究,分别建立线性规划模型,提出有效不等式加速模型的求解,对特殊情况提出多项式时间内可解的最优算法、对一般情况提出贪婪的启发式算法并进行最坏性能分析。有关钢铁企业吊机调度问题,谢谢等[11-12]就双吊机和多吊机调度问题进行了建模和性质分析,并分类讨论,他们侧重于研究吊机间的避让问题,并没有考虑吊机与生产设备之间的衔接。本文将吊机调度与多阶段生产调度问题集成考虑,提出了一类带有吊机运输的流水车间作业的最小化最大完工时间问题。

1 问题的定义及描述

以实际生产为背景,本文的问题描述如下:问题由吊机运输和生产2个阶段组成,吊机运输阶段,位于存储区域的工件(通常是铁水包、钢包等被吊物件)要由吊机运输至生产机器进行生产,生产阶段共有m台不同功能的机器(炼铁、炼钢、精炼、连铸、轧制等)。给定一个需要调度的n个工件的集合N={1,2,…,n},初始时刻所有工件都位于存储区域等待吊机运输。由于吊机只能架设在固定的轨道上,因此每个生产环节都配备一台吊机。每台吊机一次只能运输一个工件。这些吊机初始时刻也位于相应的存储区域。工件的运输时间是与工件相关的,即工件j需要的被吊运输时间为tj,j=1,2,…,n,吊机的空移动时间为常数t,假设工件的装载和卸载时间已包含在运输时间内。

数学符号定义如下:

N----被吊物件(工件)的集合{1,2,…,n};

m----系统中加工机器总数或吊机数目;

p(i,j)----工件j(j=1,2,…,n)在机器i(i=1,2,…,m)上的加工时间;

t(i,j)----吊机将工件j装载移动到机器i的时间;

t----吊机的空移动时间;

C(i,j)----工件j(j=1,2,…,n)在机器i(i=1,2,…,m)上的完工时间;

Cmax(H)----启发式算法H得到的最大完工时间;

Cmax(H*)----最优调度H*的最大完工时间。

本文研究的问题,如果不考虑吊机的运输,则该问题退化为经典的m台机器流水车间调度问题中的最小化最大完工时间问题。使用Graham等[13]的三元组表示法,该问题经典的调度问题可以表示为Fm‖Cmax。早在1954年,Johnson[14]研究了2机流水作业F2‖Cmax问题,提出并证明使用Johnson规则在O(nlbn)时间内即可求得该问题的最优解。当机器数增加到3台时,Garey等[15]证明F3‖Cmax问题是强NP-难的。因此即使不考虑吊机调度,本文所研究的问题是强NP-难的,也就是当问题规模增大,求解问题的算法不能在合理的时间内得出最优解。

2 启发式算法及渐近性能分析

基于求解经典的3机流水作业车间调度问题的算法,提出吊机与多阶段生产协调调度问题的启发式算法H。

第1步 将机器上加工时间与吊机运输时间之和排序,选出前m-1个最小的工件,将该工件作为第一个被加工工件,安排在剩余n-1个工件之前加工;

第2步 剩余的n-1个工件的加工顺序任意选择;

第3步 计算该调度的最大完工时间。

该启发式算法的时间复杂性为O(n)。

以下证明给出,当问题规模充分大时,即n→∞,该启发式是渐近最优的。

定理1 给定工件加工时间与吊机运输时间和为p(i,j)+t(i,j),i=1,2,…,m,j=1,2,…,n,为独立同分布随机变量,定义其连续分布密度函数在区间(0, 1]为φ(·)。在概率为1的情况式(1)成立。

(1)

为证明定理1,首先给出如下引理,该引理由Xia等[16]提出并证明。

引理1 基于定理1给出的参数,对于每个工件j,j=1,2,…,n,有

(2)

式中,a=2, 3, …,m, w.p.1表示在概率为1的情况下成立。

证明(定理1) 将工件按照启发式算法生成的序列重新编号,结合问题下界不等式CLB≤Cmax(H*),有

Cmax(H)-Cmax(H*)≤Cmax(H)-CLB。

(3)

结合式(1)和引理1,可以得到

由于

|θ1+θ2+…+θn|≤|θ1|+|θ2|+…+|θn|,

(5)

式中,θi为任意数,i=1,2,…,n,则有以下不等式成立:

结合引理1,有式(7)成立,

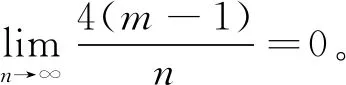
(7)

我们有

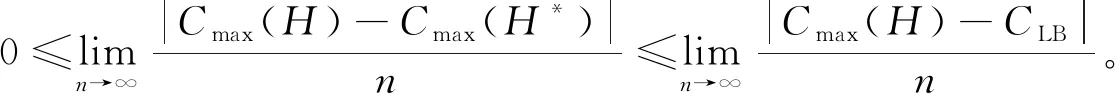
(8)

根据大数定律,结合式(8),可得定理(1)。

推论1 基于定理1的假设,对于问题Fm‖Cmax,任意给定的排序S,有

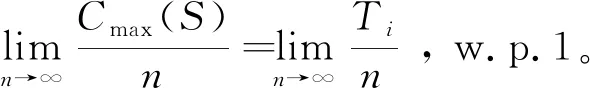
(9)

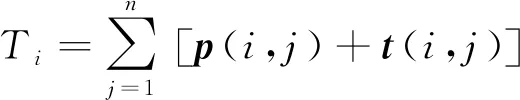
证明 将所有工件按照它们在第1台机器上的加工顺序重新编号。有

结合定理1及引理1的证明,可以得到式(9)。

在本文提出的启发式算法中,除第一个工件之外,其余工件的顺序可以随机排列,则该启发式算法的渐近最优性不会因为剩余n-1个工件排列顺序的改变而改变。以下的定理将给出证明。

定理2 启发式算法的渐近最优性不会受最后n-1个工件排列顺序的影响。

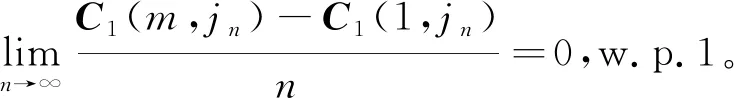
(11)

类似地,可以证明

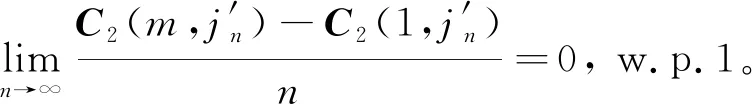
(12)

注意到式(13),

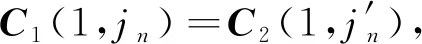
(13)

由式(11)～(13),进一步根据大数定律,得到如下结论:

(14)

定理得证。

3 数值计算实验

启发式算法的计算实验在Pentium-Ⅳ的PC机上运行,使用VC++6.0编程,所选择操作系统为Windows XP,CPU为2.40 GHz,内存为1 GB。

由本文理论证明可知,随着工件数目的不断增加,当其趋近于无穷大时,启发式算法的性能与最优调度等价。为了测试中等规模的问题实例,将随机生成问题所使用的参数,其中取机器数、吊机数m∈{3, 5, 10},工件数n∈{100, 200, 500, 1 000}。工件的加工时间以及吊机的移动时间在[1, 10]之间均匀分布。对于每一种参数的组合,分别进行10次随机测试,然后取其平均值。表1中,将启发式算法得到的目标函数与问题的下界进行了比较。表中结果为目标函数值Cmax(H)与其下界比值的平均值。

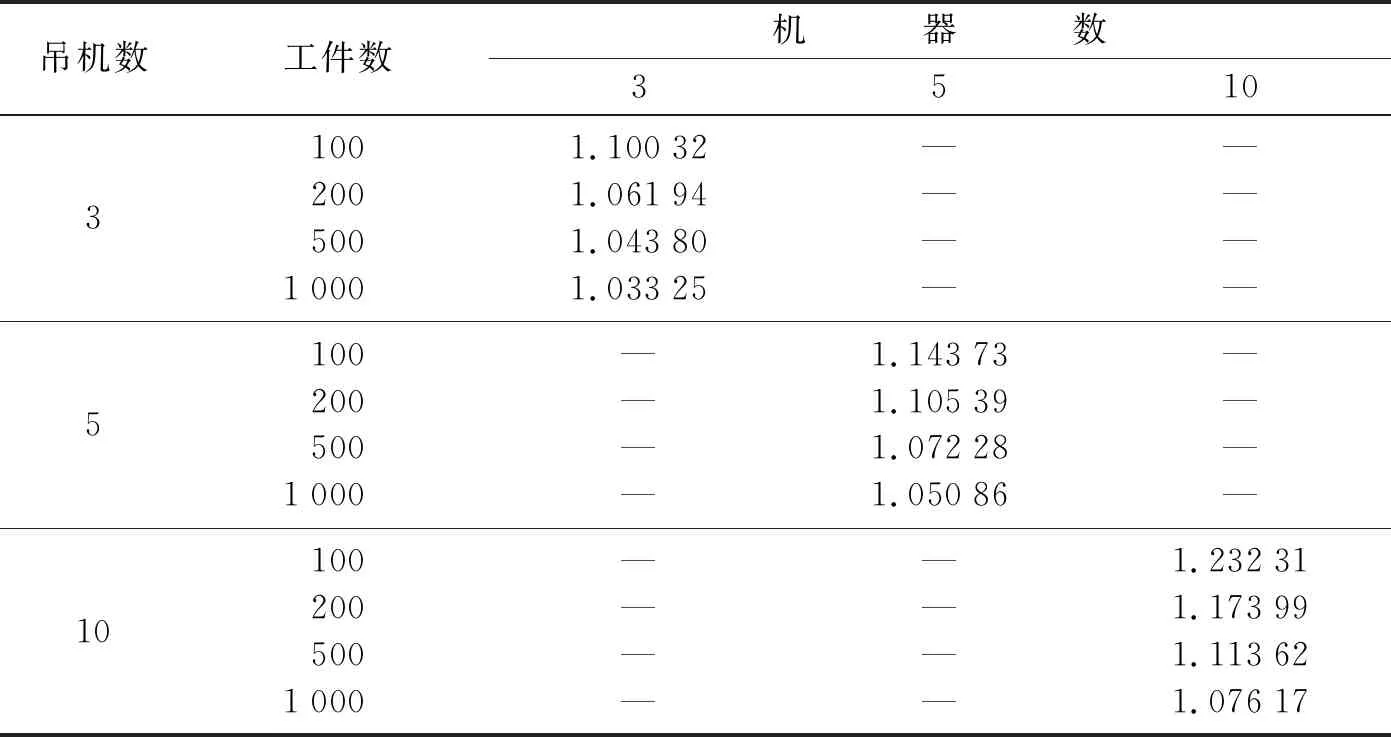
表1 启发式仿真实验结果

从图1可以看出,随着机器数的减少启发式算法与下界的比值接近于1,也就是说目标函数值随着机器数的减少而越来越接近其下界值。这是因为机器数越少,调度过程中产生的空闲时间越少,从而减小了目标函数值与其相应的下界值之间的误差。对于固定的机器数,已经证明了随着工件数的增多,目标函数值越来越接近其下界值。

图1 比值下降趋势

4 结 论

本文研究了钢铁企业生产总流程中有吊机参与生产的最小化最大完工时间问题,提出了一个启发式算法,并进一步证明当工件数目趋近于无穷大时,该启发式是渐近最优的。为了进一步验证该理论结果,提出了该问题下界,证明了该下界的渐近最优性。最后,通过数值计算实验验证了该启发式的渐近最优性。未来的研究将进一步详细讨论吊机参与车间加工的具体实施细节及多吊机之间避免相互碰撞的问题性质。