基于深度学习的运动想象脑电信号识别方法*

宋春宁, 盛 勇, 宁正高

(广西大学 电气工程学院, 广西 南宁 530004)

0 引 言

脑—机接口(brain-computer interface，BCI)技术是一门多学科融合的新型人机结合技术。目前较为普遍的是利用大脑特定活动产生的脑电(electroencephalogram,EEG)信号控制外部电子设备，其基本过程是首先使用电极采集到脑电信号，再经过放大、去噪、滤波等一系列预处理后，最后利用特征提取与分类算法将信号解码成控制设备的指令。有效提出脑电特征并准确分类是BCI的关键。研究发现,当人进行单侧肢体运动想象时大脑主感觉运动皮层的特定频段的能量会出现变化，这类现象被称为事件相关去同步(event-related desynchronization,ERD)及事件相关同步(event-related synchronization,ERS)[1]。基于时频分析方法的左右手运动想象脑电信号分类效果要由于单纯的时域或频域分析方法。在基于左右手运动想象脑电信号识别方法中，文献[2]使用短时傅里叶变换(short-time Fourier transform，STFT)时频图像结合卷积神经网络(convolutional neural network,CNN)与SAE(stacked autoencoder)模型，其识别效果优于普通CNN;文献[3]使用小波变换时频图像结合CNN进行分类，使用C3及C4电极进行实验，验证了添加CZ电极会降低分类器的识别效果。文献[4]使用STFT时频图像结合CNN与支持向量机(support vector machine,SVM)，效果优于传统的滤波器组共空间模式(filter bank common spatial patern,FBCSP)，但其分类耗时较高。传统的时间—频率方法主要包括:STFT、小波变换(wavelet transform，WT)、S变换(S transform)等。

由于STFT窗函数宽度固定不变，窗太窄虽然会有高的时间分辨率但会导致频率分辨率差;窗太宽则会导致时间分辨率过低，不利于脑电信号的时频特征提取。WT的分析结果并不是真正的时间—频率谱，从而导致信号特征的精确度有一定的问题。S变换是STFT与WT的继承与发展，加入了WT法的多分辨率分析思想，有效克服了STFT时窗固定的缺点，能较好地适应非平稳信号。S变换能同时在时域和频域内提供信号良好的局部时频特征，因此,它适合用于具有特定节律特征的运动想象脑电信号的分析，而且还不需要考虑小波基函数选择问题。

CNN是一种非常有效的图像识别方法，在语音识别、计算机视觉、图像处理等方面取得了不错的成绩，在脑电信号分类领域也有研究[5～7]。通常CNN的最后一层可以看成是一个线性分类器，但却不是一个最优的分类器。Huang G B等人[8]在2004年提出了一种单隐层网络学习算法，称为极限学习机(extreme learning machine,ELM),与传统的单隐含层网络相比，ELM在保证学习精度的前提下比传统的学习算法速度更快，泛化性能好等优点。针对CNN泛化能力稍差、较易陷入局部极值点的不足之处，本文采用CNN和ELM相结合的方法，使用ELM取代CNN的最后一层。

在脑电信号采集过程中，受试者受疲劳和精力分散的影响，很难长时间保持良好的实验状态，很难获得足够和优质的被试标记数据。在分类问题中，分类模型面对小样本训练集能力往往受到限制。文献[9]使用高斯噪声作为信息源输入进一个基于快速傅里叶变换(FFT)的系统来产生脑电信号，但此方法忽视了脑电信号的时域特性。文献[10]将不同时间段的脑电信号进行拼接构造新的数据，虽然保持了时域特征然而忽视了脑电信号的频域特性。

针对以上问题本文提出一种基于ACGAN(auxiliary classifier generative adversarial networks)的数据增强方法，即使用ACGAN模型进行时频特征图像的扩增来提高小样本数据下分类模型的分类性能。

1 S变换基本原理

S变换是地球物理学家Stockwell R G在1996年提出的，是连续WT和STFT的发展，适用于非平稳信号的分析[11]。

信号X(t)的S变换定义如下

(1)

(2)

式中ω(τ-t,f)为高斯窗口，f为频率，τ为控制高斯窗口关于时间轴t的位置参数。

其逆变换公式如下

(3)

由式(1)和式(2)可知，S变换是在继承STFT原理的基础上采用了宽度可变的高斯窗函数。高斯窗函数ω(t,f)是时间和频率的函数，窗宽与频率呈反比，这使得窗函数在低频区域具有良好的频率分辨率，在高频区域具有良好的时间分辨率。

2 CNN-ELM网络结构

2.1 ELM

ELM网络结构如图1所示。

图1 ELM模型

对于给定样本(xi,yi)∈Rn×Rm(i=1,2,…,N)，有激励函数为g(ai,bi,x)和隐节点数目L个，ELM网络模型可以表示为

(4)

式中ai为输入权值;bi为隐含层的偏差;βi为连接隐含层与输出层的输出权值;Oj∈Rn为网络输出值。当激励函数g能够以零误差逼近任意N个样本时，可以将式(4)表示为矩阵形式

Hβ=T

(5)

(6)

式(6)等价于求解Hβ=T的最小二乘解，即寻找最优的输出权值β为

β=H+T

(7)

式中H+=HT(HHT)-1为隐含层输出矩阵H的广义逆矩阵。

2.2 CNN-ELM结构与参数

本文将CNN与ELM相结合，将ELM取代CNN的最后一层，其结构如图2所示。

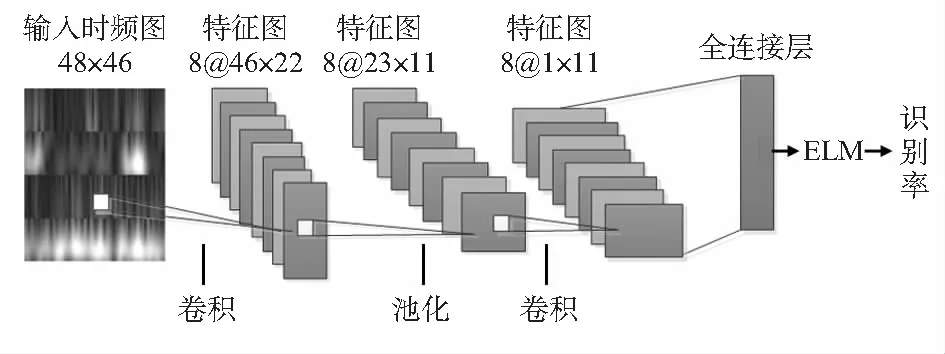
图2 CNN-ELM模型结构

本文CNN两个卷积层分别使用不同形状的卷积核，以便更好地提取图像特征。网络模型第1层为输入层，输入图像大小为48×46;第2层为卷积层，该层有8个卷积核，其卷积核的大小为[3×3]，设置步长为大小为[1×2]，使用二维卷积核是为了更好地提取图像的时频特性;第3层为最大池化层，大小为[2×2];第4层为卷积层，该层有8个卷积核，卷积核的大小为[23×1];最后为ELM。网络的训练过程如下:先采用梯度下降法调整CNN的参数，当训练误差小于一定值时停止训练，之后将CNN全连接层提取的特征作为ELM的输入用于ELM的训练。当ELM训练完成后，将它取代训练完成的CNN的最后一层，整个分类网络也就形成了。

3 实验ACGAN模型结构与参数

ACGAN是在GAN的基础上由Odena A等人[12]在2016年提出的一种新的辅助标签GAN。ACGAN损失函数包含两部分第一部分Ls是面向数据真实与否的最大似然估计如式(8)，第二部分Lc则是面向数据分类准确性的最大似然估计如式(9)。在ACGAN的训练中，优化的方向是希望判别器使得Ls+Lc尽可能大，而生成器使得Ls-Lc尽可能大。式(8)、式(9)如下

Ls=E[logP(S=real|Xreal)]+E[logP(S=fake|Xfake)]

(8)

Lc=E[logP(C=c|Xreal)]+E[logP(C=c|Xfake)]

(9)

表1实验使用的ACGAN其具体的结构如表1所示。ACGAN的输入、输出图像大小均为 48×46。模型训练批量大小为30，生成器第一层为全连接层输出尺寸为(30，24，23，128);第二层为上采样层输出尺寸为(30，48，46，128);第三层为卷积层输出尺寸为(30，48，46，128);第四层为卷积层输出尺寸大小为(30，48，46，64);第五层为卷积层输出尺寸大小为(30，48，46，1)。判别器第一层为卷积层输出尺寸大小为(60，24，23，32);第二层为卷积层输出尺寸大小为(60，12，12，64);第三层为卷积层输出尺寸大小为(60，6，6，128);第四层为两个全连接层，神经元个数分别为 1(判断真假) 和 2(2分类)。

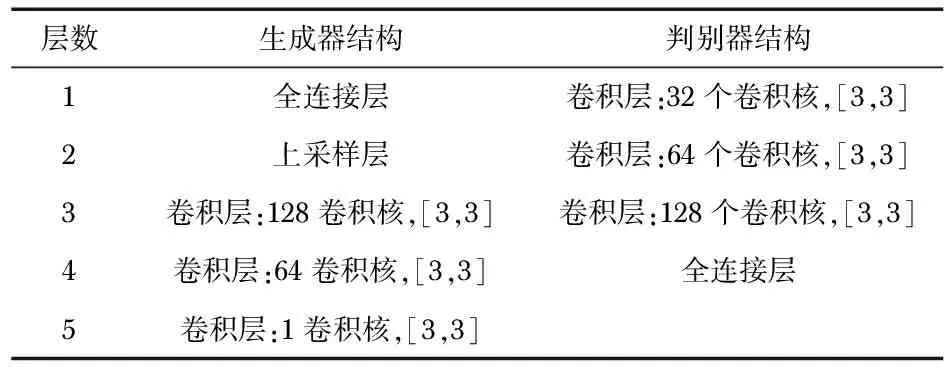
表1 本文ACGAN的生成器与判别器结构

4 实验过程与结果分析

4.1 实验数据来源

实验采用的左右手运动想象脑电数据来自BCI Competition II，BCI Competition III和BCI Competition IV。前一数据集共包含一名女性受试者，该实验的任务是按照箭头提示进行左右手运动想象来控制一个反馈条移动，每9 s采集一次，所有的试次(Trials)均在同一天完成，总共280个试次，其中想象左右手运动各140个试次。实验采集了C3，C4，CZ三个电极的脑电信号，信号的频率为128 Hz。三个数据集的实验过程的详细描述，如文献[13]所述。实验选取C3，C4电极的8～13 Hz及18～24 Hz频段图像进行组合，其大小为尺寸48×46，组合图像如图3所示。

图3 组合特征图像

4.2 CNN-ELM实验结果

为检验本文方法的性能，选用BCI Competition II竞赛数据采用五折交叉验证法和训练集测试集比例1︰1分别进行实验。实验结果如表2所示，该表选用对应文献中的最优结果。STFT+CNN-SAE是文献[2]中采用的方法，先用STFT方法进行时频特征提取，然后使用CNN-SAE模型进行特征分类。WT+CNN是文献[3]中采用的方法，先用WT方法进行时频特征提取，然后使用CNN模型进行特征分类。文献[14]使用WT结合小波神经网络(wavelet neural network,WNN)，由于存在过拟合问题，进行数据增强后识别率为91.1 %。由表2可以看出本文模型的识别率要优于文献[2]和文献[3]及文献[14]所提出的方法的识别率。

表2 BCI Competition II数据识别率

在BCI Competition III数据集上，分别选取被试者O3，S4，X11分别选取320,540,540个样本采用五折交叉验证法进行实验。表3列举了不同文献在上的识别率，可见本文的识别率要优于其他方法。

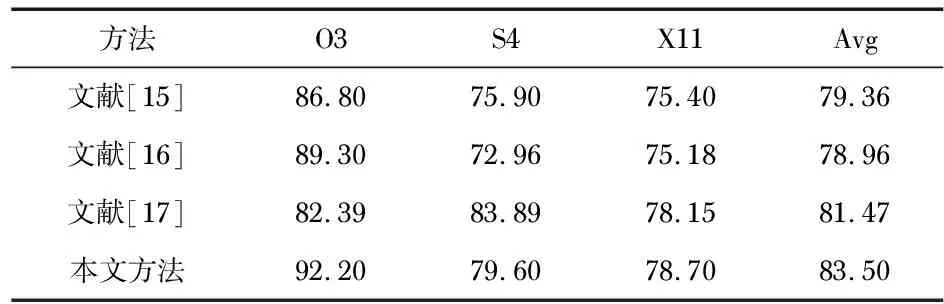
表3 BCI Competition III数据识别率 %

4.3 数据增强实验

实验选用BCI Competition IV数据集中5名受试者进行实验。数据增强实验分为训练过程与测试过程。训练过程将由ACGAN的生成器产生出新的样本数据，新数据用于扩增原始数据后用于分类器的训练。测试过程使用训练好的分类器对测试集进行预测，从而得出分类器在测试集上的识别准确率。选取每名受试者200个样本作为训练集用于训练ACGAN，其余520个样本作为分类器的测试集。

为了验证数据增强的效果，实验扩增了原始的200个数据，分别加入了新的200，400，600，800个新生成的样本,其实验结果如表4和图4所示。表4列出了5名受试者在不同扩增数据下的平均识别正确率，可知原始数据未扩增时分类器的平均识别正确率为76.3 %，当扩增400个样本时平均识别正确率78.2 %达到最大。从图4可以直观看出最初加入200个新样本受试者B04，B05，B08以及B09在测试集上的识别正确率得到了提升，而在之后随着生成样本的加入各位受试者的识别正确率走势也有所不同。当加入的生成样本远大于原始样本时分类器更多的去拟合生成样本的分布，而一定程度上忽视了原始样本的分布，观察平均识别正确率可知,当添加的新样本数量大于600时识别正确率会逐渐降低。

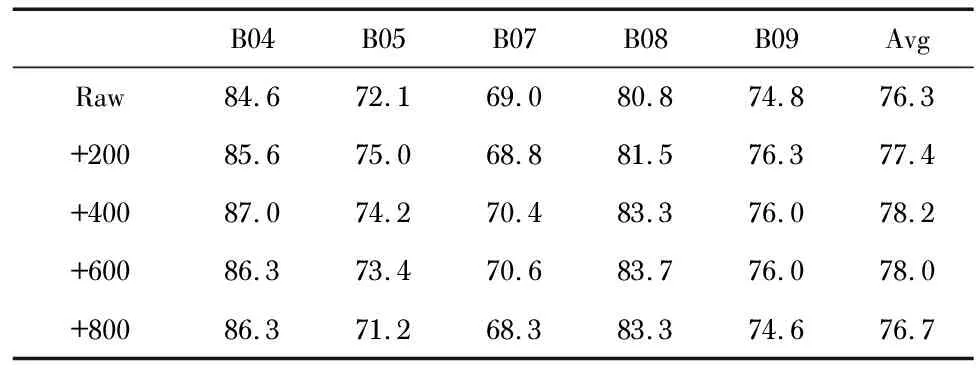
表4 数据增强实验结果

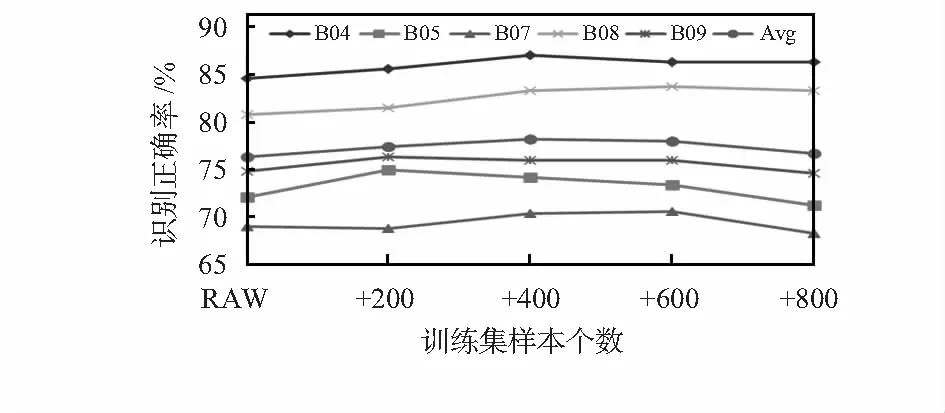
图4 数据增强实验结果

5 结束语

基于运动想象的BCI是众多BCI范式中的重要组成部分，提高脑电信号的识别精度是BCI技术从实验室研究走向实际应用的关键之一。本文研究了利用ELM方法实现左右手运动想象脑电信号的自动分类。采用的CNN-ELM模型具有模型简单，准确率高的特点，采用的数据增强方法丰富了小样本数据集样本的数量提高了识别率。实验表明CNN结合ELM提高了识别率，具有较好的泛化性能，在一定程度上满足了更高要求BCI系统的需求。