无人机巡检系统中高频效的混合波束赋形方法

凌 欣，李民政

（上海电机学院电子信息学院，上海 201306）

0 引言

无人机具有体积小，易远程操作和实时监控的优点，可用于对输电线路的巡检。与传统的人工巡检相比，其具有成本低、巡视范围广、工作效率高，并能降低巡检人员工作强度和危险性的优势［1］。

无人机根据控制系统发布的巡检任务和飞行命令，利用其搭载的高清摄像机采集图像视频信息并回传到接入节点，再由无线网关连接到地面控制端数据中心，然后进行视频数据分析，接着进行故障定位和判断故障类型，并为后续采取措施提供依据。

通常情况下，无人机获取的视频图像分辨率较高，可准确进行故障定位和故障类型判断，因此无人机和地面数据中心之间需要高速率通信链路［2］。毫米波频段具有丰富的未采用的大带宽，在带宽限定的前提下，比较适用于高速率监控视频数据的传输，但由于毫米波通信的路径损耗严重，限制了远距离传播，因此利用无人机配备的大规模天线阵列，采用波束赋形技术来获取复用增益、提高频谱效率，以满足监控视频数据高速传输的需求；同时还能得到分集增益，抵抗毫米波通信链路的路径损耗。因波束赋形技术是应用传感器阵列实现定向信号发送或接收的信号处理技术，在毫米波频段能够在某个特定角度增强信号，在另一个特定角度减弱信号从而实现某个角度的定向发送，波束赋形能够同时在发送端和接收端实现空间的选择性，而全数字波束赋形技术性能虽好，但随着天线数目增多，射频链路的开销也随之增大。为降低成本和提高性能，采用混合波束赋形技术，发送端和接收端的模拟波束赋形矩阵都由移相器实现，在下行链路中，波束赋形分成了低维度的数字预编码器和高维度的模拟预编码器，这种结构明显降低了硬件开销，并且能够接近全数字波束赋形的性能。

文献［3］中研究了四节点（源、目的、移动中继和窃听）系统中的安全传输问题，无人机作为移动中继，通过联合优化中继轨迹和中继发射功率来最大化保密率；文献［4］中研究了基于干扰的主动监听的鲁棒波束赋形设计问题，其中全双工合法监视器试图窃听无人机认知无线电网络中辅助对之间的可疑通信链路，在合法监视器的发射功率和初级接收机的干扰温度约束下，最大限度地提高可达到的窃听率；文献［5］中提出了一种自适应波束设计策略来解决在无人机飞行过程中由于风引起的不稳定波束指向问题；文献［6］中研究一种基于无人机的非正交多址系统其中无人机充当全双工中继，帮助基站和两个非正交多址用户之间的通信，通过联合优化波束赋形和时间分配比使整个系统的和吞吐量最大化；文献［7］中研究了一种基于无人机的无线传感网络，其中一个无人机在空中飞行，通过分布式波束赋形从一组传感器采集数据，传感器向无人机发送和共享数据，通过联合优化无人机的航迹设计和传感器的发射功率随时间的分配，实现数据平均吞吐量的最大化和传输中断概率最小化；文献［8］中研究了无人机作为空中基站与地面用户之间的毫米波通信，提出了一种有效的波束跟踪方案来预测具有移动性的波束方向；文献［9］中提出一种多天线基站蜂窝连接多无人机网络的波束赋形、用户关联和无人机高度控制的联合框架，设计了一种分层迭代算法最大限度地提高无人机在地面用户设备速率约束下的最小可达速率。

以上研究无人机多作为中继或直接与地面用户通信，采用波束赋形技术来提高各性能如传输速率吞吐量等，与无人机将信息传输给基站，再由基站传输给数据中心不同的是，通过构建Mesh 网络，无人机搭载的通信设备作为网络节点可随时与构建的Mesh 网络进行通信，并且在输电线路巡检中，对使用混合波束赋形技术提高无人机回传通信链路的频谱效率从而提高回传视频分辨率的研究较少。多数研究是对回传以后的视频图像进行处理，识别图像中的故障点，若前期能够提高回传视频图像的分辨率，会使得图像处理识别工作更加准确。基于以上分析，采用一种启发式的混合波束赋形技术来处理无人机与接入节点之间频谱效率最大化问题，以满足高分辨率视频图像对传输速率的需求。

本文做如下定义：()H表示矩阵的共轭转置，()-1表示矩阵的逆，Tr()表示求矩阵的迹，()*表示复共轭，()′表示矩阵去掉某列的子矩阵，||表示矩阵的绝对值，log()表示求公式的对数值，ij表示第i个传播簇中第j条散射体射线，k，l表示矩阵的第k行与第l列，Cz×d表示一个z乘d维复空间。

1 系统模型

1.1 系统描述

无人机与无线接入节点之间的通信场景如图1 所示，无人机在距离输电线路30～50 m 的高空，无人机巡检获取的数据将实时回传到安装在杆塔上的无线接入点。考虑到毫米波频段的路径损耗问题，相邻杆塔之间的间距设置为5 km［10］。

图1 无人机巡检架构Fig.1 Architecture of UAV patrol

由于无人机航迹与输电线路基本平行，因此通信链路中收发信号涉及波达角（Angle of Arrival，AoA）和波达方向（Direction of Arrival，DoA）时，假设水平角度不变，主要考虑俯仰角。如图2 所示，混合波束赋形架构采用大规模的多输入多输出（Multi-Input Multi-Output，MIMO）系统，无人机通信模块配置Nt根发射天线，无线接入点端配置Nr根接收天线，收发两端都配有NRF条射频链，满足min(Nt，Nr)>NRF，假设发送的数据流矢量s，长度为Ns，满足E{ssH}=INs。

图2 多输入多输出毫米波传输链路系统框架Fig.2 Architecture of MIMO millimeter wave transmission link system

调制后的符号首先通过NRF×Ns阶的数字预编码矩阵FBB进行基带预编码，然后利用移相器在模拟电路中实现了一个Nt×NRF阶的模拟预编码矩阵FRF。最终形成发送端信号，经过信道传输至接收端，接收端进行解调，接收信号y在经过模拟和数字合并器处理后的接收符号矢量y［11］可表示为：

其中：n是满足零均值和协方差为σ2的高斯分布的加性噪声矢量，H是无人机与接入点之间的信道传输矩阵。用WBB和WRF分别表示数字合并矩阵和模拟合并矩阵。

模拟合并矩阵和模拟预编码矩阵通过在收发端由具有调相功能的移相器实现，因为调幅能力有限，所以模拟预编码矩阵和模拟合并矩阵均满足恒模约束|[FRF]kl|=1，|[WRF]kl|=1。

1.2 信道模型

信道模型与文献［12］相似，毫米波传播信道链路有NC个簇，每簇有NR个散射体。考虑毫米波通信系统均匀线性阵列间距为半波长，基于几何的信道模型，收发两端信道传输矩阵H可表示为：

其中：αij为第i个传播簇中第j条散射体射线的复增益，ar()和at()分别表示发射天线阵列和接收天线阵列对第i簇第j条射线的归一化响应，其中分别表示到达角和发射角。

1.3 优化问题

在带宽有限的条件下，为了实现高分辨率视频数据传输，需要尽可能提高无人机回传通信链路的频谱效率。因此，混合波束赋形设计的目标［13-14］是在发射功率约束下使得系统的频谱效率最大化，优化目标函数如式（3）所示：

其中F1=FRFFBB，W1=WRFWBB。式（3）中收发端的预编码器和合并器具有耦合性，且是非凸约束的NP（Nondeterministic Polynomial）难问题。难以直接得到优化解。为此，将收发端预编码器与合并器解耦，分别求解发端的混合预编码器和收端的混合合并器。假设接收端混合合并器已固定，则式（3）的优化问题可以简化为：

显然，式（4）的优化问题仍然是非凸约束的NP 难问题。为此，假设模拟预编码器FRF固定的情况下先求解数字预编码器的优化解，然后再通过迭代算法来寻找局部最优的模拟预编码器。如此，式（4）的优化问题可进一步简化为：

其中U1=HFRF。式（5）中数字预编码器的优化解可以通过文献［15］中所提出的注水算法求得：

其中：Q为的最大奇异值对应的右奇异向量集，ϕ是分配给每个流的功率对角矩阵。对于大规模MIMO 系统，由文献［12］可知模拟预编码器FRF满足列向量的正交性，即，若进一步假设所有数据流的功率相等，即，则最佳预编码器为，由于Q是酉矩阵，所以。

综上，在获取最优的数字预编码矩阵FBB后，求解发送端模拟预编码器的优化问题可表述为：

考虑到式（7）中约束条件的解耦特性，采用迭代坐标下降算法来求解模拟预编码器，为了得到式（7）中目标函数的FRF，由文献［11，16］的研究，式（7）中的优化目标函数可转换为：

其中为去掉第l列的FRF的子矩阵。

假设模拟预编码部分的所有元素除FRF外都是固定的，则模拟预编码器元素在第k行、第l列，当φkl=0 时最优解FRF(k，l)=1，在其他情况下：

式（10）中模拟预编码器可以通过迭代算法求得，初始值设置为1（Nt×NRF），然后根据式（10）更新模拟预编码器中的每个元素，直到算法收敛到FRF的局部最优解。本文方法根据文献［16］的推导，旨在解决功率约束下发送端的预编码问题，由于在该方法的每个元素更新步骤中，式（7）的目标函数增加（至少不减少），保证了该算法的收敛性。求解发送端模拟预编码器流程如图3 所示。

图3 启发式算法流程Fig.3 Flow chart of heuristic algorithm

综上已经求得了无人机端混合预编码的问题，接下来，假定混合预编码器已经设计好的情况下，设计满足整体频谱效率最大化的接收端的混合合并器。与发射端同样的方法，假设数字合并器最优的情况下求解模拟合并器，再为该模拟合并器寻找最优数字合并器。模拟合并器的设计问题可以表示为：

其中U2=HFRFFBB(FRFFBB)HHH，这个问题与式（7）中的模拟预编码器设计问题求解方式相同，可以看出模拟合并器通常满足，因此可以将问题（11）近似为式（7）中的模拟预编码器设计问题，使用相同的算法求解WRF，式（11）可以转换为：

最后，在发送端的预编码器以及接收端的模拟合并器已知的情况下，通过最小均方误差法求得最优的数字合并器解为：

2 仿真分析

仿真环境是在窄带大规模MIMO 系统场景下，因无人机要传输图像，数据量大，带宽设置为6 MHz，工作中心频率假设为28 GHz，无人机以8 m/s 的速度沿着输电线路飞行，在整个模拟过程中，收发端均部署了一个半波间隔的均匀线性阵列，因无人机与接入点之间不存在障碍物，所以只有视距传输路径。本文方法（标记为“UAV-point”）与纯数字波束赋形（标记为“FD”）方法［14］和正交匹配追踪（Orthogonal Matching Pursuit，OMP）方法［17］在不同天线数和数据流数下对频谱效率和误比特率进行了测试对比分析。无人机与接入点之间信道模型各参数设置时，设定群簇数NC=5，散射体数NR=10，发射角和到达角均服从拉普拉斯分布，仿真过程中迭代次数设置为500，在误比特率的对比分析中，采用四进制绝对移相键控（4PSK）调制解调信号，输入的信号经过调制、信道噪声，解调后，最终的输出信号与输入信号之间的误比特率，所有的仿真均在Matlab 中进行。

图4 显示了当信噪比（Signal-to-Noise Ratio，SNR）在-15～5 dB 变化时，发送端与接收端天线数均为64，Nt=Nr=64，Ns=NRF=2 和Ns=NRF=4 时的频谱效率对比。从图4中可以看出，两种情况下，本文方法的性能与纯数字波束赋形性能相比非常接近，与OMP 方法相比频谱效率要高出很多，并且随着射频链路数目增加，三种方法的差距越来越明显。射频链路数量的增加在提升性能的同时成本与功耗也随之增加，所以应用在无人机巡检时需综合考虑。

图4 Nt=Nr=64，射频链数与数据流数为2和4时波束赋形方法的频谱效率与信噪比Fig.4 Spectral efficiency and SNR of beamforming method with 2 RF links and 4 data streams are 2 and 4，andNt=Nr=64

图5 显示了当信噪比在-15～5 dB 变化时，射频链路数均为4，而发送端与接收端的天线数为32 和64 两种情况下频谱效率的对比，即Nt=Nr=32 和Nt=Nr=64 时，从图5 可以看出，当收发端天线数目不同时，随着天线数目的增多，频谱效率在不断地提高，仍然要比OMP 方法频谱效率高出很多，但是相较于射频链路数目增加带来的频谱效率的变化，天线数目地增加带来的频谱效率的变化要小一些。

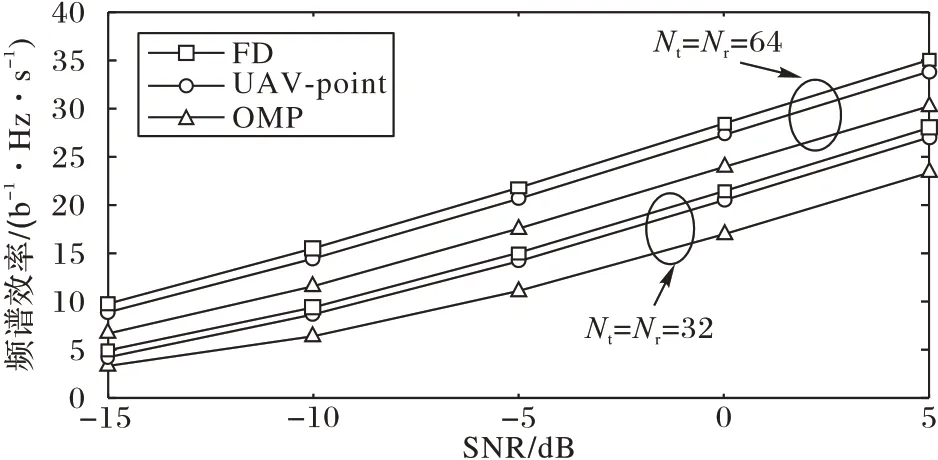
图5 Ns=NRF=4，发送端和接收端天线为32和64时波束赋形方法的频谱效率与信噪比Fig.5 Spectral efficiency and SNR of beamforming method with 32 send antennas，64 receiving antennas，andNs=NRF=4

图6 显示了当信噪比从-15～5 dB 变化时，射频链路数均为4，发送端与接收端的天线数均为64，而数据流数为2 和4两种情况频谱效率的对比，即Nt=Nr=64，NRF=4，Ns=2 和Ns=4。从图6 中可以看出，当数据流数增加时，三种方法的性能均提高，本文方法更接近于纯数字波束赋形方法，OMP方法的频谱效率仍要比本文方法低很多，并且随着数据流数的增加差距越来越明显。

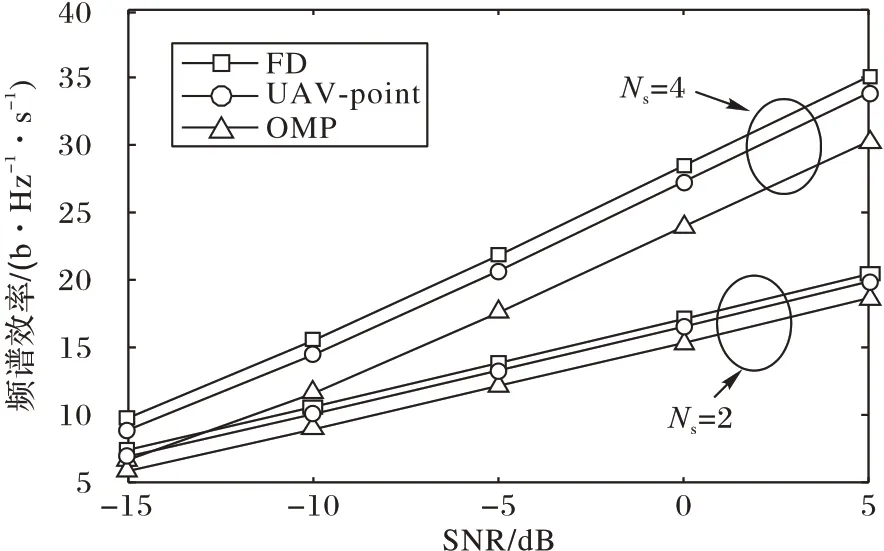
图6 NRF=4，Nt=Nr=64，数据流数分别为2和4时波束赋形方法的频谱效率与信噪比Fig.6 Spectral efficiency and SNR of beamforming method with 2 and 4 data streams，andNRF=4，Nt=Nr=64

图7 显示了当信噪比在-15～5 dB 变化时，收发端天线数均为32，数据流与射频链数均为4，即Nt=Nr=32，Ns=NRF=4 时，不同方法误比特率的对比分析。通过图7 可以看出，与OMP 方法相比，本文方法获得了更好的平均误比特率性能，与纯数字波束赋形方法相比，在SNR=-5 dB 时均可达到接近于0 的误比特率。

图7 Nt=Nr=32，Ns=NRF=4时不同波束赋形方法的误比特率与信噪比Fig.7 Bit error rate and SNR of beamforming method withNt=Nr=32，Ns=NRF=4

3 结语

本文针对无人机输电线路巡检中的通信子系统问题，构建Mesh 网络，在毫米波频段对无人机与部署在杆塔上的Mesh 节点之间的视频回传通信过程进行研究，采用启发式方法分别解耦收发端预编码器与合并器，解决优化过程中非凸约束的NP 难问题。仿真结果表明，与OMP 方法相比，所提方法在不同的天线数目与射频链数下频谱效率均得到了明显的提高且更接近于纯数字波束赋形性能，视频分辨率也随之提高，可为研发实用的输电线路无人机巡检无线通信系统设备提供参考。