基于率失真特性的视频编码优化算法

郭红伟，樊香所，刘帅，韦相，赵伶俐

（1.红河学院工学院，云南蒙自 661100；2.电子科技大学信息与通信工程学院，成都 611731；3.广西科技大学电气与信息工程学院，广西柳州 545006；4.电子科技大学资源与环境学院，成都 611731）

0 引言

高效视频编码（High Efficiency Video Coding，HEVC）是继H.264 之后的国际视频编码标准，其在相同编码质量下比前一代视频编码标准节省了近一半的码率［1］。视频编码标准规定了输出比特流的句法结构和对应解码器，而对于编码器结构和实现模式没有具体要求。这种开放性使设计者可以根据实际应用需求灵活制定编码策略，以实现最优的编码性能。

从2013 年HEVC 发布以来，许多研究关注于HEVC 编码器优化。文献［2-4］中主要研究快速模式选择：文献［2］中根据层间相关性判断可能的块划分深度，从而减少率失真（Rate-Distortion，R-D）优化过程中需要检测的帧内预测模式数；文献［3］中提出一种基于纹理特征的预测模式选择和编码单元划分快速帧内预测算法；文献［4］中针对屏幕内容特征，通过对大量最优编码模式数据的训练，提出基于机器学习的快速帧内模式选择算法。上述几种算法以牺牲一定的压缩性能来降低编码器运算复杂度。

此外，一些研究关注于在不改变码流句法结构的情况下，通过优化编码资源分配进一步改善HEVC 编码器压缩性能［5］。文献［6］中根据HEVC 低延迟编码配置下的参考关系，分析了编码帧之间的率失真依赖性，提出自适应量化参数（Quantization Parameter，QP）级联算法。同样在低延迟编码配置下，文献［7］中构建虚拟图像组（Group of Pictures，GOP），分析了GOP 内和GOP 之间的率失真依赖关系，提出一种有效的量化参数级联算法，进一步提升了压缩性能。针对随机接入编码配置，文献［8］中建立依赖失真模型，然后把该模型应用到帧级量化参数自适应算法设计。文献［9］中通过大量实验分析了编码过程中跳过（Skip）模式概率与率失真依赖的相关性，建立了精确的时域失真传播模型，提出了基于时域失真传播模型的自适应量化算法。不同于HEVC中分级固定QP 结构，上述几种算法根据视频内容变化自适应地设置量化参数，获得了一定的率失真性能提升。

针对严格码率约束下的编码资源分配，文献［10］中提出了基于R-λ模型码率控制的最优比特分配算法，减小了码率控制过程中的率失真性能损失，但其压缩性能仍略差于不开启码率控制的HEVC 基准编码器。由于编码单元之间的时域率失真依赖关系，对当前编码单元的编码决策会影响后续参考它的编码单元可达到的率失真性能。为此，文献［11］中分析了HEVC 低延迟编码结构中的失真传播关系，提出基于信源失真时域扩散模型的拉格朗日乘子自适应算法，通过改善对后续编码影响较大的像素块编码质量，在一定程度上提升了全局率失真性能。类似地，文献［12］中对屏幕内容编码提出了加权率失真优化算法，其仍然是通过自适应调节基本编码单元的拉格朗日乘子进行编码优化。不同于直接调整QP 的算法，上述几种算法通过拉格朗日乘子自适应实现编码比特资源优化分配。

自适应量化参数和自适应拉格朗日乘子的视频编码优化方法探索率失真依赖性并用于优化编码比特资源分配，一定程度上改善了HEVC 编码器压缩性能，但这些方法没有考虑到编码单元自身的率失真特性，率失真性能提升较为有限。本文通过分析HEVC 不同层级编码单元的率失真特性，建立幂函数率失真模型，再结合文献［11］中的信源失真时域扩散模型提出一种采用二次编码框架的率失真优化算法。本文的创新工作主要是结合编码树单元的率失真模型和信源失真时域扩散模型建立帧级比特预算约束下的最优比特资源分配方程，从而自适应地调整编码树单元的拉格朗日乘子和量化参数，最终实现了显著的压缩性能提升。

1 率失真特性分析

根据率失真理论，率失真函数给出了限定失真条件下的最大压缩性能，视频编码作为一种典型的有损压缩方式，其压缩性能同样受到率失真函数的限制。事实上，由于编码技术以及硬件条件有限，当前视频编码远未达到率失真函数的理论值；另外，混合视频编码框架下，可选择的编码参数集有限。因此，实际视频编码可达到的最佳率失真点是离散的，这些最佳率失真点的外包络线称为最优可操作率失真曲线，如图1 所示。

图1 可操作率失真曲线Fig.1 Operational rate-distortion curve

与理论率失真曲线相比，可操作率失真曲线更能反映视频编码中的码率与失真关系，但要获得确切的可操作率失真曲线非常困难，涉及多次编码要求极高的运算量和超长延时。一种可行的可操作率失真曲线描述方法是建立基于函数的率失真模型，为此本文以HEVC 测试模型（HEVC test Model，HM）16.7 为平台进行实验统计和分析，建立不同层级编码单元的率失真模型。具体地，编码器配置文件采用encoder_lowdelay_P_main.cfg，参数设置服从视频编码联合协作小组（Joint Collaborative Team on Video Coding，JCT-VC）制定的通用测试条件（Common Test Conditions，CTC）［13］，从CTC 建议的Class D 和Class E 中选择RaceHorses（416×240）和FourPeople（1 280×720）两个视频序列进行编码，统计4 个输入QP（22，27，32，37）编码后序列级、帧级和编码树单元（Coding Tree Unit，CTU）级的码率和失真。码率统一用每像素的比特数（bits per pixel，bpp）度量，失真用原始视频像素与重建视频像素亮度分量的均方误差（Mean Square Error，MSE）度量。

通过对4 个可操作率失真点进行函数拟合得到如图2～4所示序列级、帧级和CTU 级R-D 曲线，可以发现幂函数能非常好地表示HEVC 不同层级编码单元的率失真特性。图中R2是函数拟合相关系数，R2的值越接近1 则幂函数与可操作R-D 曲线的吻合度越好，通过对大量实验数据统计得出序列级和帧级的R-D 曲线与幂函数的相关系数均高于0.9，绝大部分CTU 级的R-D 曲线也能很好地由幂函数表示。需要说明的是，图4（d）中4 个码率点均为0.000 2 bpp，这是因为序列FourPeople 是背景固定的会议场景，不管编码QP 取22 还是37，第2 帧第4 个CTU 均由前一帧对应位置的像素直接表示，即采用了skip 模式，此时的编码失真完全由参考块的质量决定。综上，除了类似于图4（d）中参考像素与待编码像素完全一致的特殊帧间预测情况外，可采用幂函数模型表示HEVC 的率失真特性：

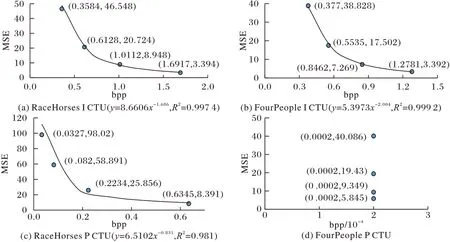
图4 CTU级的拟合R-D 曲线Fig.4 Fitted R-D curves at CTU level

式中C和K是两个模型参数。由图2～4 可见，不同编码单元R-D 模型的参数各不相同，但C和K总是大于0。

图2 序列级的拟合R-D 曲线Fig.2 Fitted R-D curves at sequence level

图3 帧级的拟合R-D 曲线Fig.3 Fitted R-D curves at frame level

2 本文算法

2.1 基于一次编码的R-D模型估计

第1 章分析得出幂函数R-D 模型能非常好地表示HEVC中CTU 的率失真特性，然而每个CTU 可能具有非常不同的模型参数。采用第1 章的4 个率失真点拟合R-D 曲线需要进行4 次编码，而且当参考帧的编码策略发生变化后，待编码帧和CTU 的R-D 曲线也会发生改变。根据视频编码的率失真优化理论［5］，编码失真对编码码率的一阶导的负数即是编码过程中使用的拉格朗日乘子，对式（1）的幂函数R-D 模型求一阶导可得：

然后联立式（1）和式（2）可求解得R-D 模型参数为：

当一帧被编码后可以获得当前帧中每个CTU 的码率和编码失真，结合编码过程中采用的λ即可由式（3）和式（4）计算出CTU 的R-D 模型参数。

2.2 依赖率失真优化

由于帧间预测编码导致编码单元之间存在时域率失真依赖关系，当前帧中不同CTU 对后续编码过程可能具有不同的重要性。为了使后续帧达到更好的率失真性能，应减小对后续编码性能影响较大的CTU 编码失真，因此编码一个CTU的最小化率失真代价过程可描述为：

式中，W用于表示当前CTU 在编码中的重要性，与时域失真传播相关。显然，越重要的CTU 其失真权重越大，编码过程中偏向于消耗更多的码率从而减小编码失真。为便于算法实现，依赖率失真优化方法通常简化式（5）为：

式（6）表示可以通过修改编码CTU 的拉格朗日乘子调节不同CTU 的编码质量。针对HEVC 分级编码结构和多参考帧设置的特点，文献［11］中通过简化16×16 像素块的失真扩散路径，提出了一种基于信源失真时域扩散模型的自适应拉格朗日乘子优化算法。在本文提出的二次编码优化中，采用文献［11］中的方法度量时域率失真依赖关系，式（6）中的权重系数Wi=1+ωi，ωi称为第i个CTU 的时域失真传播因子。

2.3 二次编码优化框架

结合编码单元的率失真特性和时域编码块之间的率失真依赖性，本节提出一种二次编码框架优化CTU 级编码比特资源分配，进一步改善了编码器率失真性能。编码过程中每一帧会被连续编码两次：第1 次按照原始HEVC 的方法编码但不输出码流，记录下每个CTU 的失真、码率和编码中采用的拉格朗日乘子，据此得到每个CTU 的R-D 模型参数；第2次编码前，结合当前帧中每个CTU 的R-D 模型和文献［11］中的时域失真传播因子建立比特分配方程，通过求解该方程得到优化后每个CTU 的拉格朗日乘子，再进行第2 次编码，并正常输出码流和存储重建图像。本文算法具体步骤描述如下：

1）获取当前帧和每个CTU 消耗的比特数以及每个CTU的编码失真。使用HEVC 默认方法由输入QP 计算当前帧的λ进行编码，记录下编码后当前帧消耗的比特数TF和每个CTU 的码率及失真。然后根据式（3）和式（4）计算得到CTU的R-D 模型参数，对于类似于图4（d）的特殊情况，设置RCTU=Clip3（0.000 5，10.0，RCTU）以简化率失真模型，运算符Clip3（a，b，c）使输出c的值不小于a并且不大于b。

2）恢复参考列表等信息并计算新的λ和QP。第1 次编码不输出当前帧的码流，也不存储重建图像。第1 次编码结束后需重置编码器中图像链表到编码当前帧之前的状态，包括恢复图像链表中的参考帧标识等。举例来说，低延迟编码配置下图像序列号（Picture Order Count，POC）为17 的帧会选择POC 为16、12、8、4 的重建帧为参考帧，但第1 次编码POC 为17 的帧后，POC 为4 的重建帧将被标记为不再作为参考帧，若不恢复该标识将导致第2 次编码POC 为17 的帧时可选参考帧只剩下POC 为16、12 和8 三个重建帧。

根据式（2）推导出第i个CTU 的码率可以表示为：

再结合依赖率失真优化过程中λi=λ/W，代入式（7）得到：

把第1 次编码当前帧消耗的比特数作为可用的比特资源数，则考虑CTU 率失真特性和率失真依赖性的比特资源分配可表示为：

其中NU是一帧中的CTU 个数，Mi是第i个CTU 中的像素数，Wi=1+ωi采用文献［11］中的方法获得。因此，式（9）中只有λ为待求解未知量。为了获得精确的数值解，采用迭代泰勒展开法（Recursive Taylor Expansion，RTE）［14］求解式（9）得到λ的值。然后，用于第2 次编码第i个CTU 的拉格朗日乘子为：

由于每个CTU 使用了不同的拉格朗日乘子进行率失真优化，相应地量化参数QP 也应该调整，因此每个CTU 的量化参数根据QP 修正技术［15］重新计算：

3）第2 次编码当前帧并输出码流和重建图像。采用步骤2）计算的拉格朗日乘子和量化参数再次编码当前帧中每个CTU，并按照编码器默认方式输出码流和存储重建图像。需要强调的是无论第1 次编码还是第2 次编码，它们参考的都是之前帧被第2 次编码后的信息，如此编码顺序设计是为了确保获得的CTU 率失真特性更加准确，因为参考帧的编码决策变化会改变待编码帧中CTU 的率失真特性。

3 实验与结果分析

3.1 实验设置

提出的二次编码优化算法被实现在测试软件HM16.7以评估其率失真性能。另外，文献［10］中的最优比特分配算法已经被JCT-VC 采纳，集成在HM16.7 的码率控制模块中。编码器配置采用低延迟B 帧（Low Delay B-frame，LDB）和低延迟P 帧（Low Delay P-frame，LDP）分级编码结构，对应配置文件分别是encoder_lowdelay_main.cfg 和encoder_lowdelay_P_main.cfg。测试序列选用CTC［13］建议的Class B、Class C、Class D 和Class E 中全部16 个视频，包括了从416×240 到1 920×1 080 不同分辨率、帧率和场景内容的原始视频序列。每个视频序列依据CTC 测试4 个码率点，即原始HM16.7 和本文算法采用22、27、32 和37 四个输入QP值，文献［10］根据原始HM16.7 的四个输出码率设置目标码率。

3.2 实验结果

表1 给出了分别从Class B、Class C、Class D 和Class E 中选取4 个测试序列在LDB 和LDP 配置下的实验数据，其中峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）是指亮度分量的PSNR值。从中可以看到，无论是LDB 还是LDP 配置，4 个测试序列在4 个码率点处，本文算法获得的PSNR 几乎都是最高的，仅在个别低码率时本文算法的PSNR值略低于其他算法，主要是因为低码率时本文算法输出码率有时略小于其他两种算法输出码率。

表1 LDB和LDP配置下的码率和PSNR对比Tab.1 Bitrate and PSNR comparision under LDB and LDP configurations

为了直观地呈现各种算法的率失真性能，根据四个码率点绘制LDB 配置下测试序列Kimono 和LDP 配置下测试序列BasketballDrill 的R-D 曲线如图5 所示，图中，横坐标bitrate 是码率，纵坐标YPSNR是亮度分量的峰值信噪比。

图5 三种算法的率失真曲线对比Fig.5 Comparison of R-D curves for three algorithms

需要说明的是，与前文所述用bpp 和MSE 度量码率和失真的R-D 曲线不同，这里的码率单位是kb/s，编码失真用PSNR 度量，因此曲线越靠向上说明率失真性能越好。可以看到，对于选取的这两个测试序列，本文算法率失真性能优于文献［10］算法和基准编码器HM16.7。对于LDP 配置下的BasketballDrill 测试序列，文献［10］算法的率失真性能优于基准编码器HM16.7；而对于LDB 配置下的Kimono 测试序列，文献［10］算法显示了较差的率失真性能。事实上，文献［10］算法是码率控制下的最优比特分配，其相较于原始的R-λ模型码率控制算法，率失真性能有所提升，但对于大部分测试序列其率失真性能略差于不开启码率控制的HEVC基准编码器。

事实上，比较视频编码的率失真性能不能仅看压缩视频的PSNR，还需要综合其编码码率进行对比。为了综合码率和失真评判不同算法的率失真性能，本文使用评价标准BD-rate（Bjøntegaard Delta bit-rate）全面客观地对比多种优化算法的性能。BD-rate 表示在相同客观质量下，测试算法相对于基准编码器的码率节省百分比，正值表示率失真性能损失，负值表示率失真性能改善，本文中的客观质量用压缩视频亮度分量的PSNR 度量。表2 给出了LDB 和LDP 配置下，文献［6］算法、文献［7］算法、文献［10］算法、文献［11］算法和本文算法相对于HEVC 基准编码器的BD-rate。其中，除了文献［10］算法和本文算法的实验数据采用HM16.7 测试以外，其他三种对比算法的实验数据从相关文献中摘录。可以看到，文献［10］算法的平均率失真性能有少许下降，这是因为文献［10］算法是码率控制下的最优比特分配，其在编码过程中受到严格的码率约束，码率控制下大部分测试序列的率失真性能有所下降。文献［6］算法和文献［7］算法根据视频内容变化自适应调节帧级量化参数获得了大约1.5%的编码性能提升，而文献［11］算法根据块级失真传播因子自适应调节CTU 级的拉格朗日乘子获得了更高的率失真性能提升。本文算法在LDB 和LDP 配置下，除了Class E 外，其他几类视频均获得最高的率失真性能提升，总的平均性能提升分别达到3.5%和3.8%，优于其他几种对比算法。

表2 不同算法相对于HEVC基准的BD-rate对比 单位：%Tab.2 BD-rate comparison of different algorithms against HEVC benchmark unit：%

测试序列Class E 是背景固定的会议场景，具有相对更强的时域率失真依赖性。因此，基于时域依赖性的率失真优化算法能获得很高的性能提升。本文提出的二次编码优化算法涉及的时域率失真依赖关系采用文献［11］中的时域传播因子度量，但所提算法对Class E 的性能提升还略小于文献［11］获得的率失真性能提升。原因主要是所提二次编码算法用到了CTU 的R-D 模型，而正如图4（d）所示，Class E 测试序列背景区域的许多CTU 编码不具有幂函数的R-D 特性，导致所提算法中的R-D 模型出现较大误差。事实上，由于会议场景视频具有很强的时域率失真依赖性，提升视频第一帧（I 帧）的编码质量，可以带来较大率失真性能改善。但为了实验对比公平性，文献［11］算法未对I 帧编码进行优化，因此本文二次编码算法也未修改I 帧的编码策略。另外，相同输入QP 情况下，所提二次编码优化算法获得较大率失真性能提升的同时其输出码率与HEVC 基准编码器基本保持一致，说明率失真特性和率失真依赖性可以被进一步地用于码率控制算法设计，在实现码率控制的同时获得率失真性能改善。

4 结语

本文提出了一种二次编码优化算法。首先采用实验统计分析得到幂函数形式的率失真模型较好地描述HEVC 不同层级编码单元的率失真特性；然后根据率失真理论得出可以通过一次编码计算每个编码单元的率失真模型参数；最后提出了一种结合CTU 的率失真特性和率失真依赖性的二次编码优化算法。本文算法有效地提升了编码器率失真性能，并且其输出码率与原始HEVC 基准编码器输出码率基本一致。本文算法中的率失真依赖性度量采用信源失真时域扩散模型估算，其需要预先读取后续帧建立时域传播链。下一步将研究在不缓存后续帧情况下通过第一次编码估计率失真依赖关系，以进一步改进视频编码优化算法。