基于路径时间差的变压器局部放电超声定位方法研究
2022-04-12孙浩飞花啸昌张冠军
孙浩飞,高 坤,花啸昌,高 峰,李 元,张冠军
(1.国网陕西电力科学研究院,陕西西安 710100;2.西安交通大学电力设备电气绝缘国家重点实验室,陕西西安 710049;3.国网陕西省电力公司西安供电公司,陕西西安 710199)
0 引言
随着电力行业的发展,电压等级不断提高,变压器内部绝缘工作电场也逐步提高。在变压器的制造、运输、安装以及运行过程中,不可避免地会产生多种绝缘缺陷[1-3]。在外施电压的作用下,变压器内的缺陷可能会诱发局部放电,导致绝缘进一步劣化,最终发展为绝缘击穿,造成巨大的经济损失。因此,局部放电的检测以及准确定位对于评估设备的绝缘状态,保障电力设备安全稳定运行具有重要意义[4-9]。
高频电流法、特高频法以及超声波法是常用的现场变压器局部放电检测方法。其中高频电流法定位技术的研究主要针对绕组的缺陷[10]。特高频法抗干扰能力强、灵敏度高,采用内置特高频探头可以取得较好的定位效果,但由于变压器箱壳可以屏蔽电磁波信号,外置特高频传感器的安装位置十分受限,在已投运的变压器上,较难安装数量较多的特高频传感器,导致定位精度无法保障[11-12]。超声波传感器具有非侵入式的安装方式、较高的抗电磁干扰能力以及经济的价格,在变压器局部放电的定位技术研究中应用广泛[13-16]。本文主要基于超声波法,对现有的变压器局部放电定位算法进行改进,提高定位的准确度。
目前,研究人员主要基于波达时间差法(Time Difference of Arrival,TDOA),利用信号从局部放电源传播至各传感器的时间差来进行空间定位。Masai H.等采用有限元法、有限差分法求解声波方程,研究了声信号在变压器内的传播特性[17]。之后研究者列写TDOA 方程组,并采用诸如最小二乘法、最速下降法和牛顿-拉夫逊法等智能算法求解[18-21]。G.Veloso 和L.E.Borges 利用遗传算法与量子遗传算法来求解非线性TDOA 方程组[22]。西安交通大学的王彦博等建立了变压器离散数值节点模型,提出了基于粒子群优化算法的超声定位方法,考虑了不同介质中超声波速度不同以及界面处波形转换的影响[23-24]。J.Jia 等通过引入折射、衍射误差系数对TDOA 方程组进行了修正,并采用半正定松弛凸优化算法求解得到放电源的坐标,减小了信号传播路径引入的误差[25]。
文献[17-25]中提到的定位算法均部分考虑了传播路径对定位准确度的影响,但并未将实测的波达时间与信号的传播路径进行对应,即波达时间并不一定来自预想的传播路径,给定位结果带来较大误差。为解决上述问题,本文建立了变压器的数值节点模型,基于粒子群优化算法提出了一种改进的局部放电定位算法。在数值节点模型中采用算法寻找从放电源到传感器的沿箱壁传播的非直达波路径与油中直达波路径,引入这2 条路径的时间差作为每个传感器的特征,将其与实测时差进行比对得到放电源的位置。
1 超声波传播特性仿真
1.1 仿真模型
为了研究局部放电产生的超声信号在变压器内的传播特性,本文建立了变压器绕组的二维轴对称有限元模型,分析了绕组、绝缘油以及外壳对超声信号传播的影响,模型如图1 所示。其中S1—S7为7 个超声传感器,用以测量该位置的超声信号。
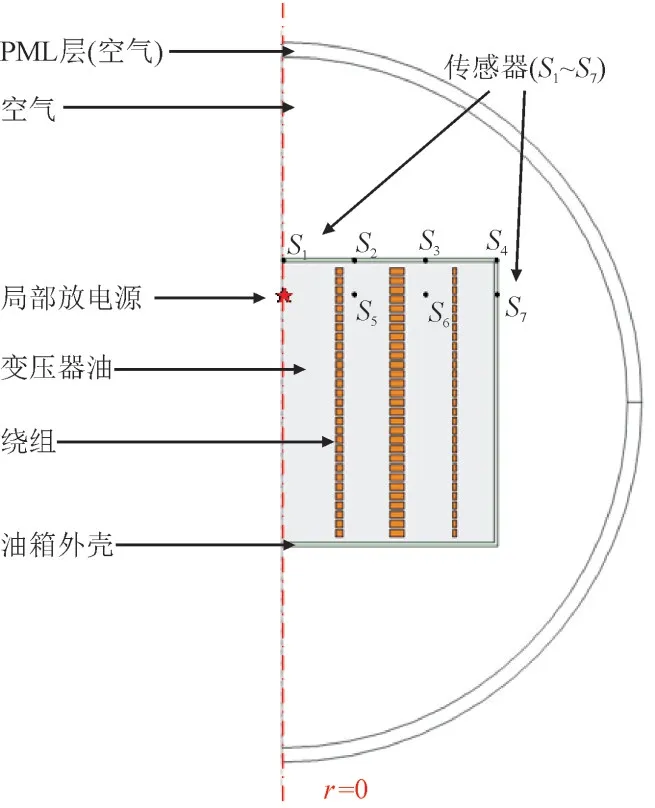
图1 仿真模型Fig.1 Simulation model
本文用点声源模拟局部放电源,用频率为80 kHz的衰减振荡脉冲模拟局放超声信号,信号的时、频域波形如图2 所示,脉冲如式(1)所示:
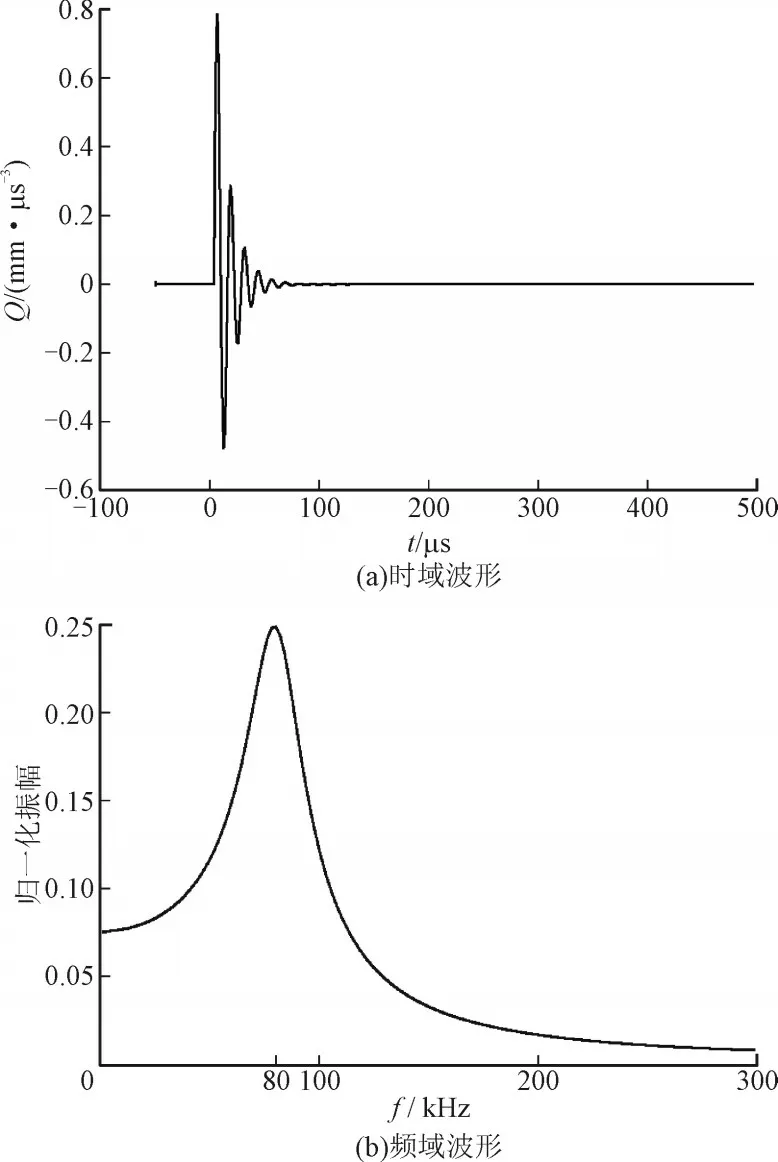
图2 局部放电源的时、频域波形Fig.2 Time domain and frequency domain waveform of partial discharge source
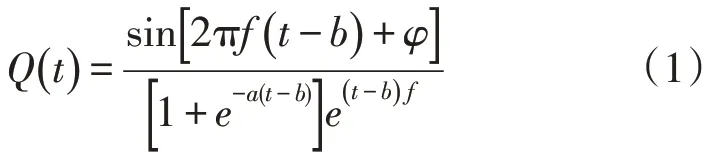
式中:Q为由点声源流出的单位长度体积流量;a为脉冲宽度因数,取a=107;b为时间补偿因子,取b=3×10-6;φ为平均值补偿因数;f为频率,取f=80 kHz。
1.2 超声波传播过程
当局部放电起始后,超声波信号的扩散过程如图3 所示。脉冲将以球面波形式的波阵面向前传播,球面波的强度与波阵面面积成反比,即与传播距离的二次方成反比。本例中所见模型的绕组为饼状绕组,可以看出在超声波向外传播的过程中,遇到绕组会产生能量衰减,但由于散射与衍射现象,仍会有较高能量的声波传出。图4 为传感器S7采集到局部放电信号的时频域波形图。
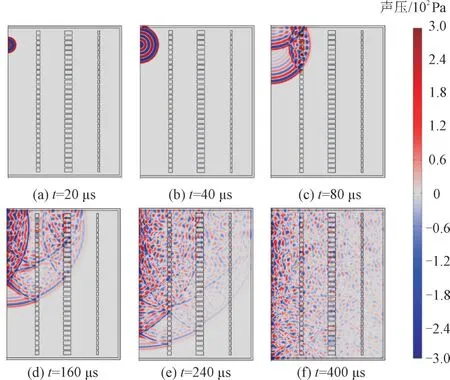
图3 超声信号传播过程Fig.3 Propagation process of ultrasonic signal
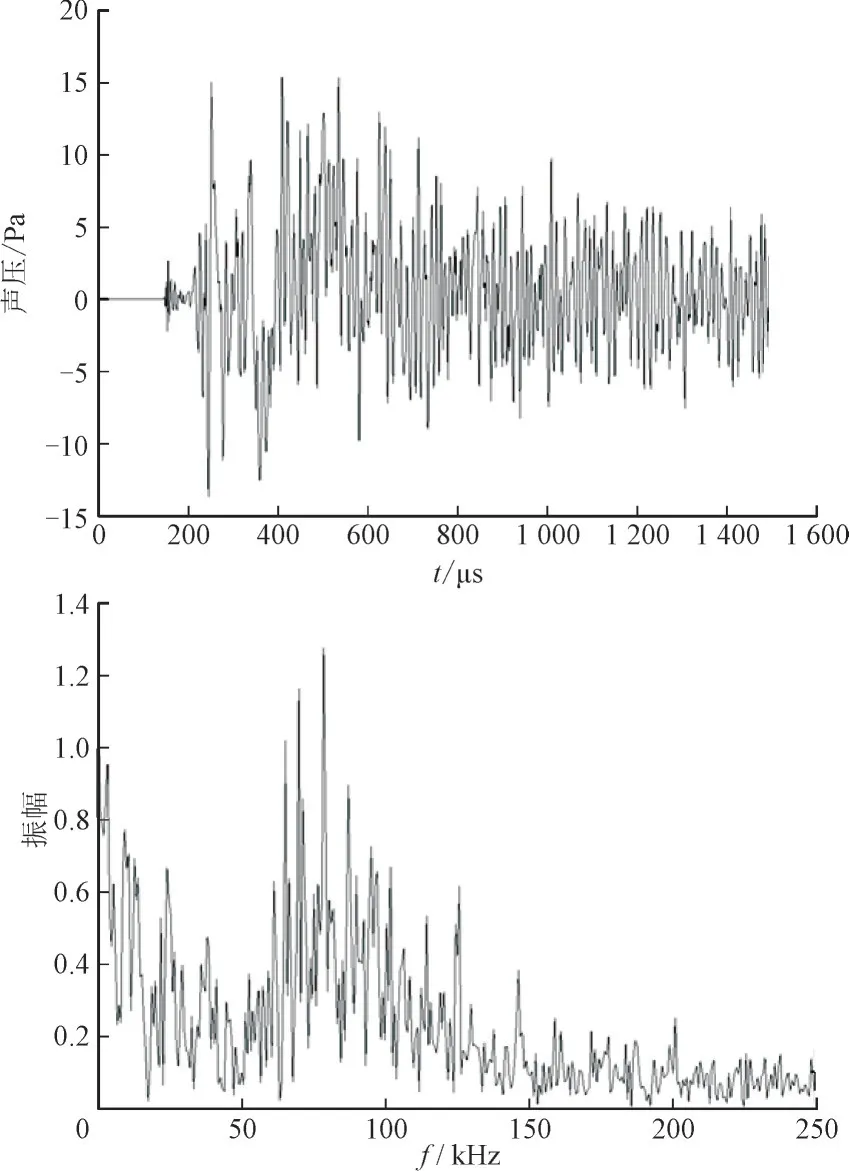
图4 传感器S7处信号的时频域波形Fig.4 Time domain and frequency domain waveform of signal at sensor S7
从图4a 可以看出,在140~200 μs 时,传感器会首先接收到频率较高、幅值较低的信号,对此信号进行傅里叶分解,发现信号的频带范围在160~240 kHz内。t=240 μs,信号会接收到幅值较高、频率为80 kHz 的信号,这是由于信号从放电源到传感器具有多条传播路径:(1)超声波信号首先按照油中的波速向上传播至变压器外壳,再按照钢中的波速沿外壳传播至传感器处,传感器在140~200 μs 内接收到的信号即来自此路径;(2)超声波信号穿过绕组缝隙直接传播至传感器处,传感器在240 μs 时接收到的信号来自此路径;(3)超声波信号通过箱壁的折反射传播至传感器的位置。传播路径的示意图如图5 所示。
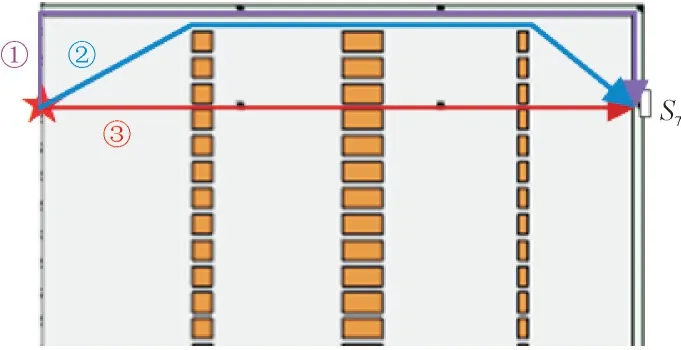
图5 超声信号传播路径示意图Fig.5 Propagation path of ultrasonic signal
2 超声信号的预处理
由仿真结果可知,沿变压器外壳传播的非直达波信号幅值较低、频率较高,沿油中直达路径传播过来的直达波信号幅值较高、频率较低。对于实验采集到的波形,准确判断直达波与非直达波的波达时间十分重要。一些研究者手动选择波达时间,但面对大批量数据不可行。本文首先对信号进行傅里叶分解,得到信号的频谱,信号的主频为f。再分别采用一个0—f的低通滤波器与一个1.5f—3f的带通滤波器对信号滤波。对低通滤波器处理后的信号,采用累积能量法可得到直达波的波达时间,对带通滤波器处理后的信号,采用短时过零率法可得到非直达波的波达时间。
图6 是实验采集到的一个典型的超声信号波形,在260 μs 之前仅有背景噪声信号,260~360 μs之间为以较快速度从变压器外壳传播而来的非直达波信号,由于超声信号在金属油箱中的传播速度远大于在油中的传播速度,因此这一部分信号扩散衰减更为严重,幅值更低且频率较高。在360 μs 之后,直达波信号或其他较强信号才陆续到达传感器,信号的幅值出现较大提升。
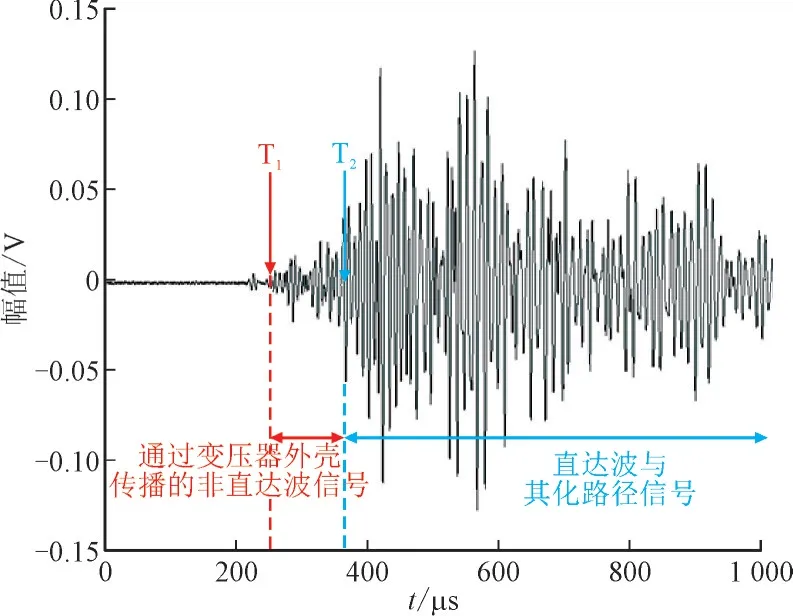
图6 典型局部放电超声信号波形Fig.6 Waveform of typical partial discharge ultrasonic signal
对信号进行傅里叶分解,频谱如图7 所示。信号的主频为100 kHz,故分别采用一个0—100 kHz的低通滤波器与150—300 kHz 的带通滤波器处理信号,处理后的信号如图8 所示。分别采用累积能量法与短时过零率算法即可得到直达波的波达时间为273 μs,非直达波的波达时间为378 μs。
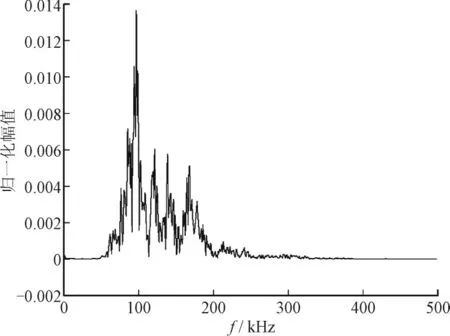
图7 超声信号频谱图Fig.7 Ultrasonic signal spectrum
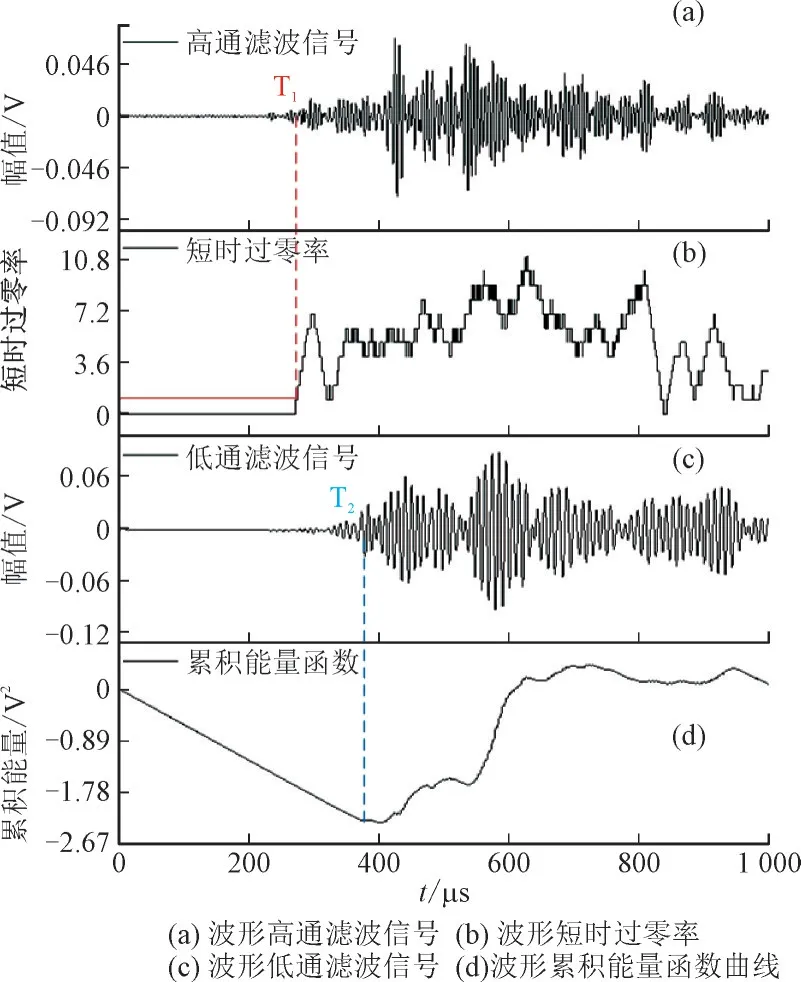
图8 波达时刻算法计算结果Fig.8 Calculation results of wave arrival time algorithm
3 局部放电定位算法
局部放电定位流程如下,首先建立变压器的数值节点模型。随机选择初始粒子作为潜在局部放电位置。之后结合数值节点模型,采用寻路算法分别计算从放电源到传感器不同路径间的时间差,将之与实测时间差进行比对,采用粒子群优化算法迭代得到放电源的真实位置。每个粒子的适应度函数F(Ni)定义如式(2)所示:
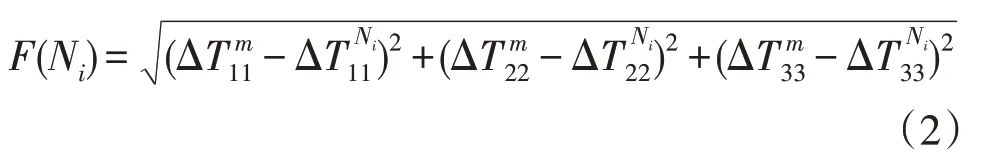
式中:Ni为待计算适应度的粒子;ΔTm11为传感器1实测接收到的超声信号沿不同路径的波达时间差;ΔTNi11为假设局部放电源位于Ni位置时,采用寻路算法计算得到的超声信号沿不同路径传播至传感器1 的时间差。ΔTm22,ΔTm33的定义方式参考ΔTm11;ΔTNi22,ΔTNi33的定义方式参考ΔTNi11。
3.1 变压器数值节点模型
建立变压器的数值节点模型可以有效地反演超声波传播过程,通过将变压器空间离散化可以简化定位的复杂性和计算量。变压器的数值节点模型主要包括铁芯、绕组、油箱外壳以及变压器油等结构。对于层状绕组,声波信号在遇到绕组后会经过多次折反射,穿过绕组的声波能量极低,故可将绕组等效建模为铜片。而对于饼状绕组,由于衍射和散射现象,传出绕组的声波能量较高,故可忽略绕组对声波传播的影响,不对绕组进行建模。变压器模型中每个节点被赋予传播参数和速度参数。超声波信号只能在变压器油和油箱壳体中传播,而无法在变压器内部金属件中传播,故将变压器内部金属部件的传播参数设置为0,变压器油与箱壁外壳的传播参数设置为1。变压器外壳节点的速度参数为超声波信号在金属油箱中的速度,变压器油节点的速度参数为超声波信号在变压器油中的速度。图9 给出了35 kV 实验变压器的数值节点模型,其中坐标轴单位均为cm,下文同。
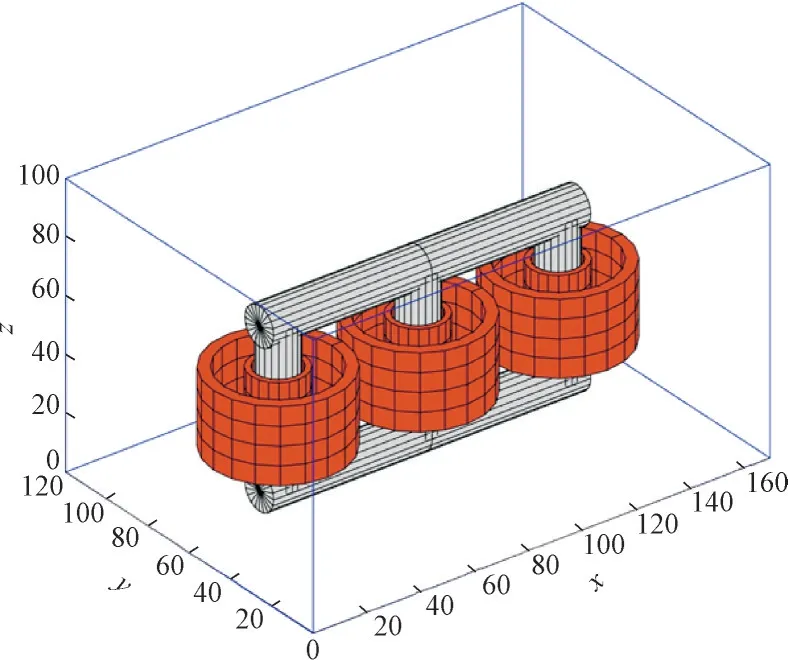
图9 35 kV实验变压器数值节点模型Fig.9 Numerical node model of 35 kV experimental transformer
3.2 路径搜索算法
建立变压器模型是为了寻找与波达时间相对应的声信号传播路径。采用A*寻路算法计算从局放源到传感器的油中直达波路径,超声信号沿此路径的衰减也最小。在变压器数值节点模型中,将变压器内部的金属结构视为超声波不可穿过的障碍物。从待选局放源开始,超声波将向其周围的124个节点传播,寻路流程如下:首先将初始节点加入开放列表中,然后不断重复如下过程:(1)找到开放列表中F值最小的点并将其作为待处理节点,F值为已走距离G与估算的该点距传感器的曼哈顿距离H之和;(2)将待处理节点加入关闭列表中;(3)对于待处理节点周围的124 个节点,如果其为障碍物或已经在关闭列表中,则忽略它。否则进行如下操作,若其不在开放列表中,将其加入开放列表,并将当前节点记录为其父节点,记录其F,G与H值。若其在开放列表中,则比较G值的大小以判断是否需要更换父节点,并更新F值;(4)当传感器节点出现在开放列表时,表示找到了路径,停止寻路。当开放列表为空时,表示从局部放电源到传感器无直达路径。通过上述算法即可较为快速地在变压器数值节点模型中寻找出局部放电源到传感器的直达波最短路径,并按照油中的波速计算波达时间。
图10 为寻路过程的演示图,其中青色路径为按照A*寻路算法寻找出的路径,红色路径为局部放电源到传感器的直线路径。由图10 可以看出,直线路径会不停穿过绕组、铁芯等内部金属结构,产生较大的幅值衰减,使得信号往往无法被传感器检测到,若按此路径进行局部放电的超声定位,将会引入较大的误差。
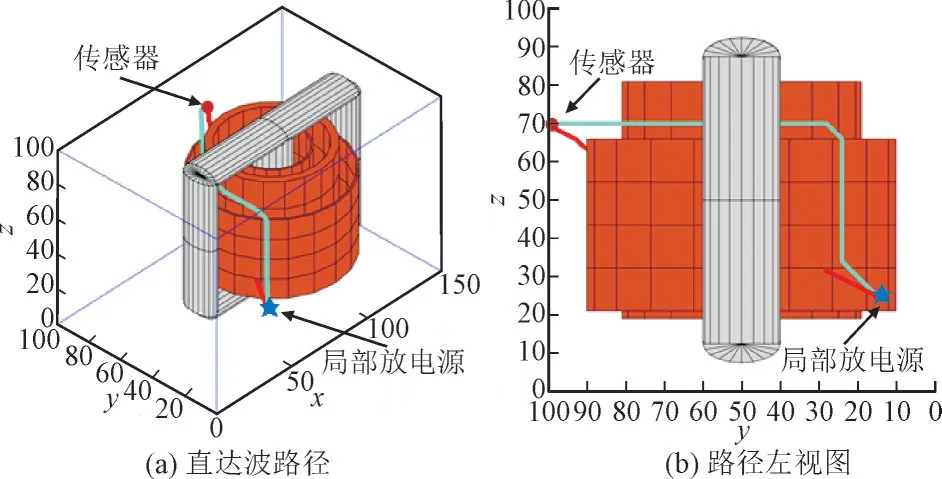
图10 直达波路径寻路示意图Fig.10 Schematic diagram of direct-wave path searching
根据IEEE 超声检测定位导则[16],非直达波的寻路算法为,超声信号首先传播至金属外壳处,再沿外壳传播至传感器处。当入射角小于14(°)时,传感器可以接收到来自直达波的横、纵波信号。当斜入射角位于14(°)~26(°)的范围内时,传感器可以接收到来自直达波的横波信号,当斜入射角大于26(°)时,油-外壳界面上声信号将发生全反射。对于范围内的任一待选节点,首先需要寻找该节点在传感器平面与其相邻平面上的投影节点,如图11 所示,进而得到纵波范围(即图中红色阴影区域)与横波范围(即图中蓝色阴影区域)。由内向外遍历上述区域内的节点,判断从局放源到该节点的油中直线路径是否存在阻挡。选取油中路径最短且未受阻挡的节点作为入射节点。由此,超声信号的传播路径可以被分为两个部分,第一部分位于变压器油中,按照油中的声速计算传播时间。第二部分位于变压器箱壁外壳中,按照钢材料中的纵波或横波波速计算传播时间。
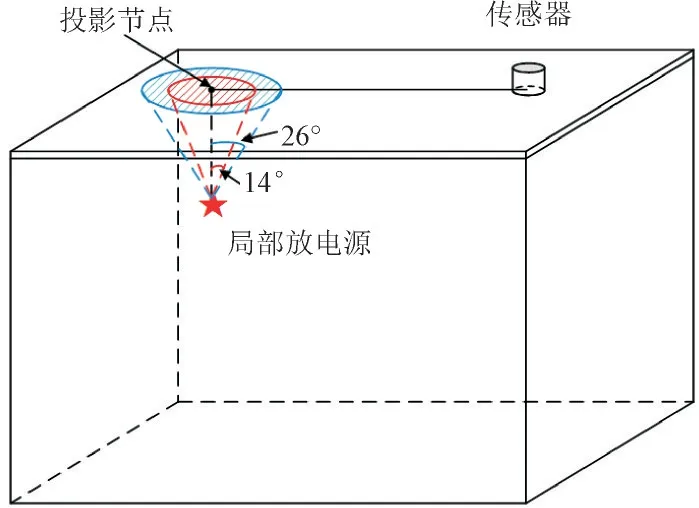
图11 非直达波路径示意图Fig.11 Schematic diagram of non-direct wave path
4 实验验证
为了验证定位算法的准确性,在35 kV 实验变压器上进行了局部放电定位验证,实验布置如图12所示。其中变压器为三相三绕组结构(图12(a)),尺寸为166 cm×115 cm×90 cm。
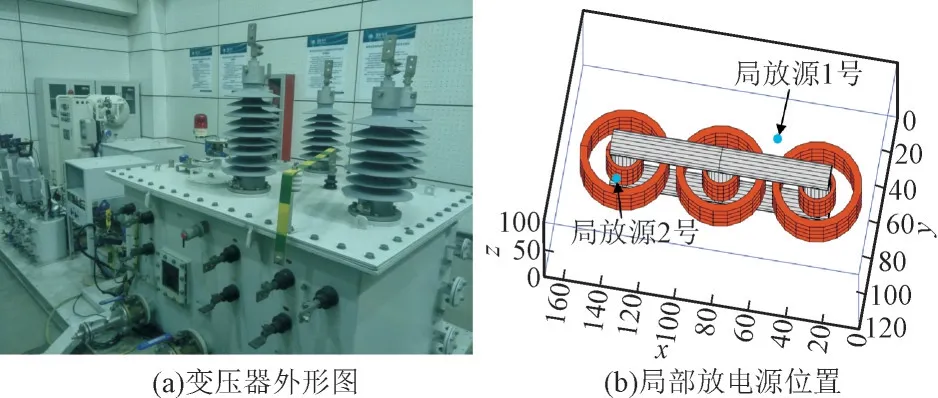
图12 35 kV变压器外形图与局放源位置Fig.12 Photograph of 35 kV transformer and location of partial discharge source
实验中,采用针尖缺陷模型产生局部放电信号,分别将缺陷放置在变压器的两个不同位置,布置方式如图12(b)所示。1 号位置位于变压器油中,具体坐标为(57,26,51)cm。2 号位置位于高压绕组内,具体坐标为(138,75,50)cm。实验使用4 个超声传感器,频段范围为100—400 kHz,通道采样频率为1 MS/s,触发阈值为35 dB。传感器的布置位置列于表1。
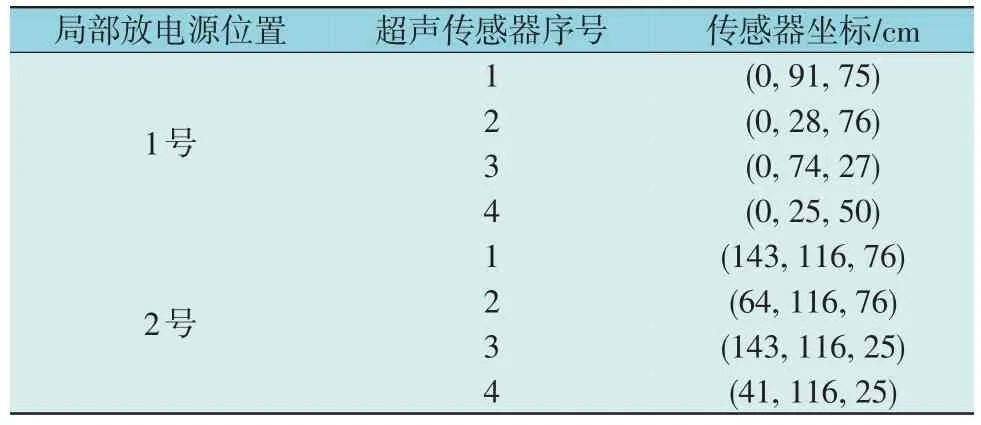
表1 35 kV变压器超声传感器坐标Table 1 Coordinates of ultrasonic sensor for 35 kV transformer
当局部放电源位于1 号时,四个传感器的声信号波形如图13 所示。传感器1 号和3 号距离局部放电源较远,直达波信号与非直达波信号的波达时间相差较大。传感器2 号和传感器4 号距离局部放电源位置较近,直达波信号与非直达波信号的波达时间差相差较小。
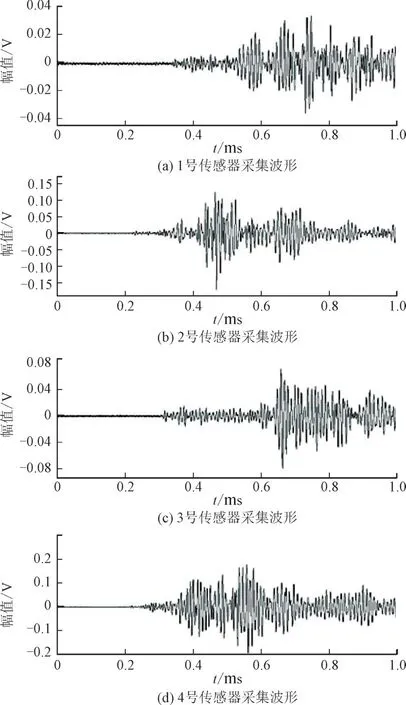
图13 各传感器超声信号波形(局放源位于1号)Fig.13 Ultrasonic signal waveform of each sensor(partial discharge source of sensor1)
当局部放电源位于1 号时,定位结果为(49,22,57)cm,定位误差为10.77 cm,信号传播路径如图14 所示。当局部放电源位于2 号时,定位结果为(132,74,42)cm,定位误差为10.04 cm,信号的传播路径如图15 所示。其中,红色路径为油中直达波路径,青色路径为沿箱壁传播的非直达波路径。
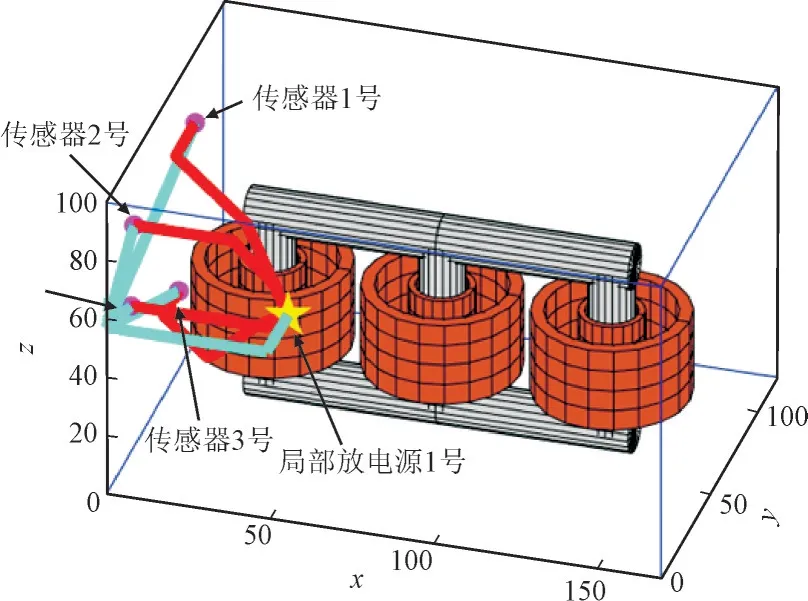
图14 局部放电源1号时超声信号传播路径Fig.14 Route of ultrasonic signal propagation of partial discharge source of sensor1
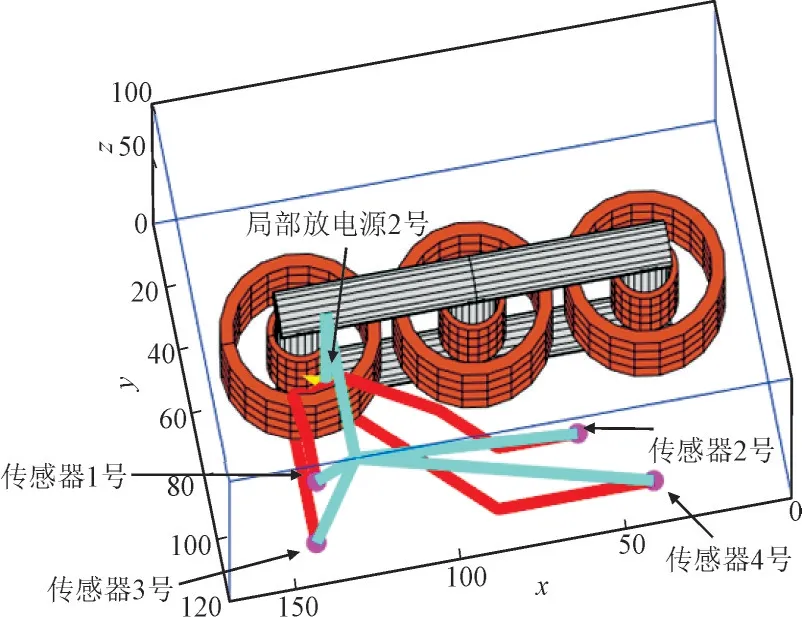
图15 局部放电源2号时超声信号传播路径Fig.15 Route of ultrasonic signal propagation of partial discharge source of sensor 2
5 结论
本文提出了基于超声信号传播路径时间差的变压器局部放电定位方法,提高了定位的准确率,有利于变压器放电故障检测与安全稳定运行。主要得出以下结论:
1)仿真研究了超声信号在变压器内的传播特性。结果表明,超声信号在变压器内具有多条传播路径,沿箱壁路径传播的非直达波信号往往先到达传感器,信号幅值较低、频率较高。后到达的油路径直达波信号幅值较高、频率较低。
2)提出了实测波形的路径时差计算方法,首先将实测波形通过低通滤波器与带通滤波器滤波。对低通滤波器处理过的信号,采用累积能量法可得到直达波的波达时间;对带通滤波器处理后的信号,采用短时过零率法可得到非直达波的波达时间。
3)建立了变压器的数值节点模型,基于该模型,提出了直达波路径与非直达波路径的寻路算法,将计算得到的路径时差与实验得到的时差进行比较,采用粒子群优化算法迭代得到放电源的位置。在35 kV 变压器上进行定位实验,验证了算法的准确性。
