基于智能负荷控制的分布式能源系统调控策略研究
2022-04-12郭新志刘英新李秋燕王利利
郭新志,刘英新,李秋燕,郭 勇,王利利
(1.国网河南经济技术研究院,河南郑州 450000;2.华北电力大学新能源电力系统国家重点实验室,北京 102206;3.国网三门峡供电公司,河南三门峡 472000)
0 引言
目前,我国较大比例能源消耗仍依赖于煤炭等化石燃料,随着我国经济社会的发展,能源需求量的大幅提高造成了大量化石能源的消耗,一定程度上制约了我国经济社会的可持续发展[1]。在能源和环境危机的双重背景下,分布式能源系统(Distributed Energy System,DES)由于其包含多种能源类型,具有环保、可靠、灵活的优点,得到快速发展[2-4]。合理调控分布式能源,对促进能源合理利用,缓解能源、环境危机,具有重要的意义。但由于DES 中新能源出力的波动性和随机性,在并网时会对电力系统产生一定冲击,因此,为减弱此负面影响,本文引入对智能负荷的合理调控。
对于负荷侧的需求分析及调控策略已取得一定的成果,文献[5-7]介绍了用户侧能量管理系统的概念,考虑用户意愿及生活习惯提出了负荷状态概率矩阵,并建立了居民用电概率模型,制定了以分布式光伏消纳最大化为目标的主动负荷需求响应方案。文献[8-10]对基于多样性保持的空调负荷群控制策略的控制特性和参数进行深入分析,建立了负荷控制代价模型。文献[11-13]提出对商业楼宇微网系统的负荷进行交互控制,通过需求响应调节微网功率平衡。文献[14]提出了基于机会约束的直接负荷控制和可中断负荷模型。但对于智能负荷的可调规模分析及其负荷特性的研究仍未形成成熟的理论方法。
目前,国内外学者已经对DES 的运行优化进行了一定的研究,王惠[15]在考虑系统碳排放的基础上,进行不同建筑负荷的DES 优化研究。曾鸣[16]在考虑需求侧资源的的基础上,对DES 的经济优化运行进行研究。任洪波[17]以光伏电池、燃料电池、蓄电池的住宅能源系统为研究对象,分析在满足住宅电力和热力需求的同时,年运行成本最小的运行策略。张俊礼[18]将启停逻辑和负荷限制等约束的各环节运行特性与经济、能效、环保等目标模型联立,建立适用于运行策略研究的滚动优化模型。张涛[19]根据冷热电负荷需求、能源价格和设备技术信息等,运用非线性整数规划方法,建立DES 的优化模型。但是,考虑智能负荷参与需求响应的DES 调控策略的相关研究较少。
因此,本文为研究DES 优化调度策略,通过综合考虑调度时段、电价水平、气象条件、控制信号等因素,运用监督学习技术训练神经网络,并对智能负荷可控规模进行分析,得出智能住宅可控有功功率函数。考虑可调度机组、潮流、风电光伏、储能系统能量平衡及旋转备用约束等约束条件,建立分布式能源管理系统模型,将智能负荷的需求响应控制信号及DES 中其他参数变量进行优化,得出DES 经济性和可靠性最优的调度策略。最后,基于国内某智能小区试点进行算例分析,利用IEEE-6 节点系统研究智能住宅参与需求响应对DES 运行的影响。
1 模型整体框架
在DES 中,用户的需求响应受多种因素影响,包括电价水平、气象条件、政策激励程度等。本文构建了智能负荷神经网络模型,综合考虑温度、电价、需求响应控制信号Lmax值、时间等因素,对Lmax值进行优化,将住宅可控有功功率代入分布式能源管理系统模型,分析调控策略。该模型的整体框架如图1 所示。其中,为负荷历史值,为负荷当前值。
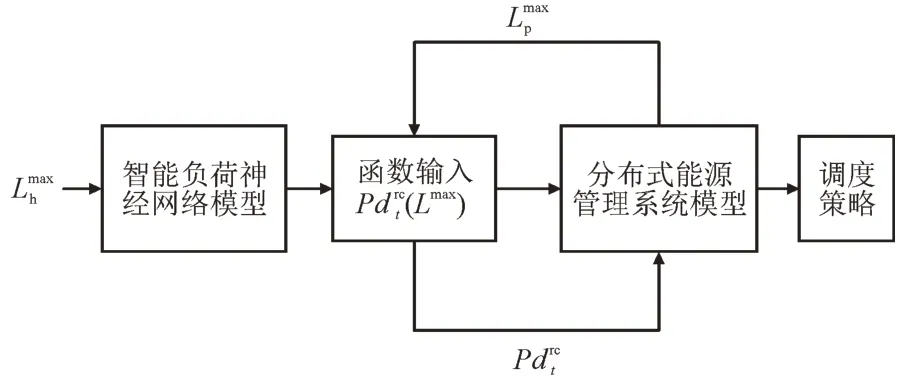
图1 模型整体框架Fig.1 Model framework
首先,在智能负荷神经网络模型中,利用神经网络训练得到关于Lmax的函数;其次,将该函数代入DES 管理模型中,优化得到,进行多次迭代,得到最优解;最后,得到住宅可控负荷、发电机组、储能装置的调控策略。
2 模型构建
2.1 智能负荷神经网络模型
考虑每个住宅均配备能源中心管理系统(Energy Hub Management System,EHMS),EHMS 通过双向通信网络与DES 相连接,DES 可以借此向EHMS 传递Lmax。因此,EHMS 可根据需求信号、天气情况及客户偏好制定住宅的负荷调度计划,进而基于家用电器及需求响应控制相关约束,使用户能源消费最小化。
为提高能源管理效率,应恰当估算住宅可控有功功率曲线,进而将需求响应模型合并到分布式能源管理系统框架中。本文基于智能电表的测量数据及实际EHMS 的仿真数据,采用监督学习技术训练神经网络[20]。最终,所估计的住宅可控有功功率神经网络被表示为时间、环境温度、电价及需求响应控制信号Lmax的函数:
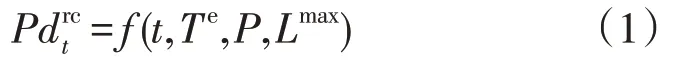
式中:t,P分别为时间、电价,是已知量;Te为环境温度,是预测值;Lmax为需求响应控制信号,是由分布式能源管理系统决定的变量。
通过改变隐藏层神经元的数值[21],利用MATLAB 软件中Levenberg-Marquardt 学习技术,基于数据训练神经网络,得出最优结果为8 个隐藏层神经元,最终得到智能负荷神经网络模型的结构,如图2 所示。其中,IPx,t指第x个输入变量在时段t对应数值;Wx,y,W′y分别为第x个输入与第y个隐藏层相关变量、第y个隐藏层对应变量的权重;,Eop分别为隐藏层神经元及的误差。
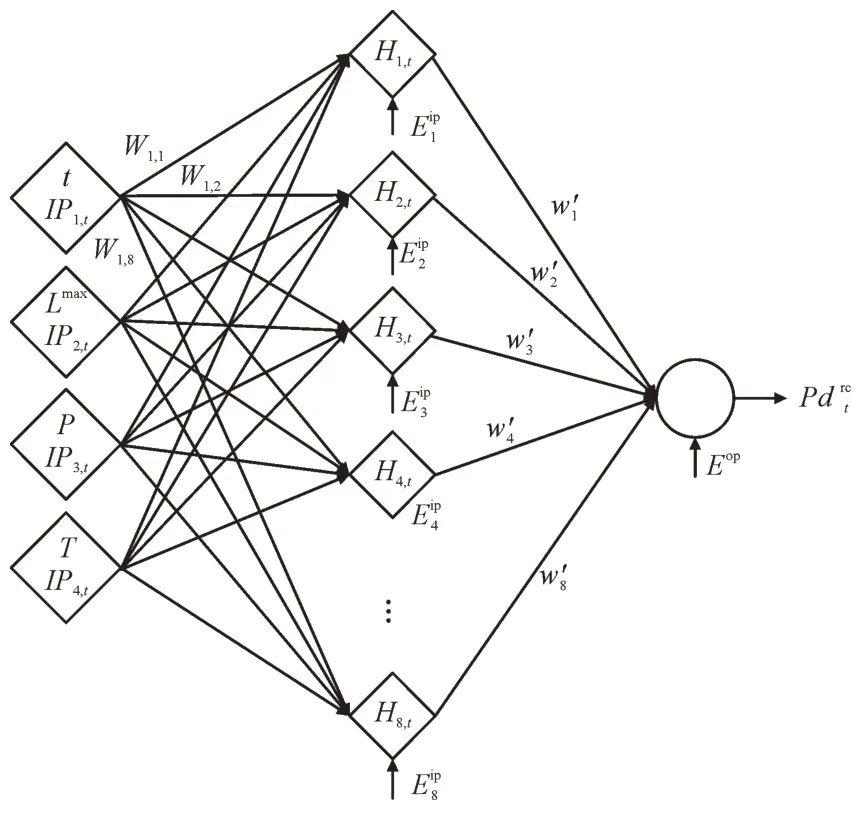
图2 智能负荷神经网络模型Fig.2 Intelligent load neural network model
训练过程结束后,将采用新的数据测试神经网络模型,以评价该神经网络的效果。神经网络模型的输出结果,即住宅可控有功功率可表示为:
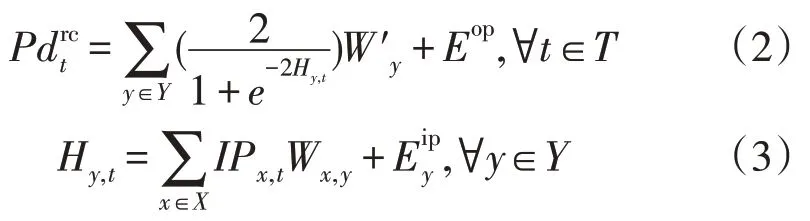
式中:T为时间周期;Y为隐藏层个数;X为输入量个数。
2.2 分布式能源管理系统模型
分布式能源管理系统的目标函数为系统运行成本最小,该成本包括发电成本、启停成本、切负荷相关成本等,如式(4)所示:
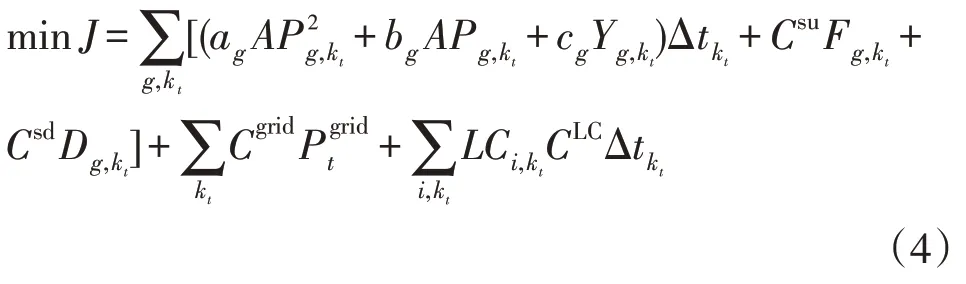
式中:ag,bg,cg分别为成本函数的二次项、一次项、常数项;为kt时段编号为g的发电机组有功功率;Δt为单位时段;为开/关次数;Csd,Csu分别为发电机组停运成本和启动成本;分别为关机、开机决定;Cgrid为主网购电价格;为从主网购电功率;为切负荷量;CLC为切负荷成本。
目标函数式(4)的约束条件如下。
1)功率平衡约束。母线的有功平衡考虑分布式电源、太阳能光伏、风机的输出,商业、居民用户负载的净功率,储能系统的充电、放电,以及网络潮流,可表示为:
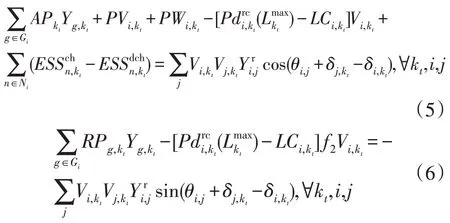
式中:Gi为节点i发电机组集合;PWi,kt为风机出力;为母线电压;为光伏机组出力;为节点ij之间的导纳;f1,f2为无功功率负荷因子;Ni为节点i安装储能数量;为发电机组无功功率;θi,j,为相位角;分别为储能系统充电功率、放电功率。
住宅负荷包含固定负荷和可控负荷2 部分[22-23],其中,固定负荷来自于可预测的用电设备,可控负荷是EHMS 中可调度的需求量。
2)机组约束。该约束包含有功和无功功率发电约束、爬坡约束、最小启停时间约束等,可表示为:
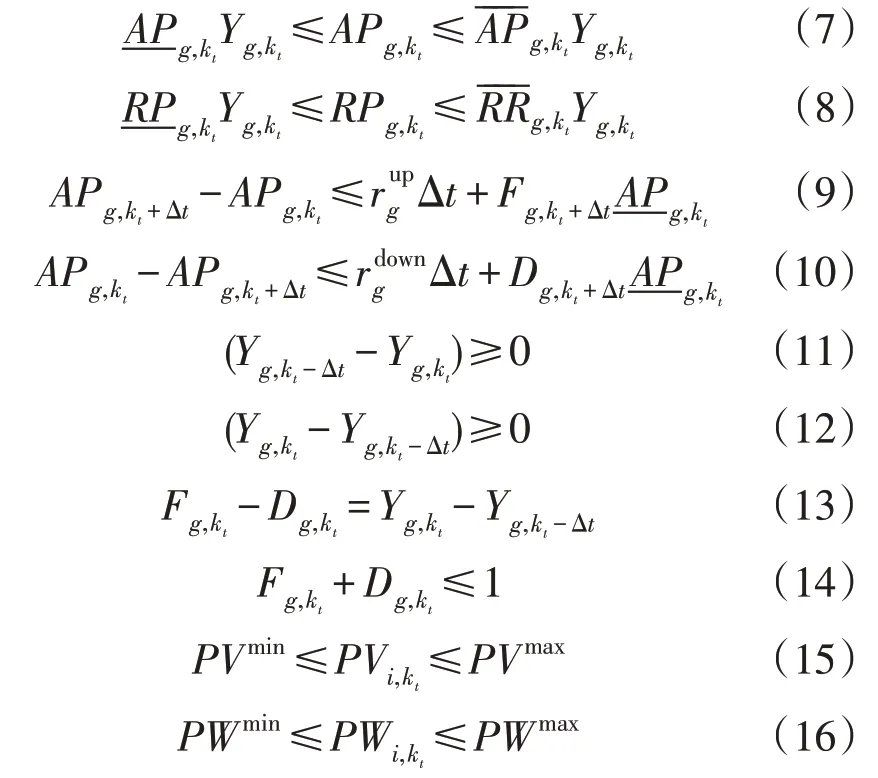
3)储能系统约束。该约束包含电力平衡约束、充放电约束及电荷状态约束[24],可表示为:

4)电网约束。该约束是为了保证母线电压及功率传输保持在特定的限制内[25]。即:

5)主网购电约束。DES 作为一个相对独立的能源系统,从主电网购电应满足一定的约束限制。即:
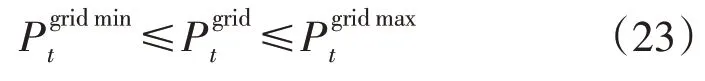
6)需求响应约束。该约束为给定时间段中的需求响应控制信号Lmax的约束为:
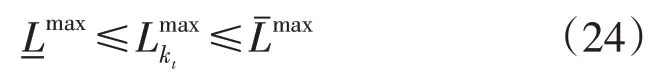
3 模型求解流程
本文模型求解流程如图3 所示。
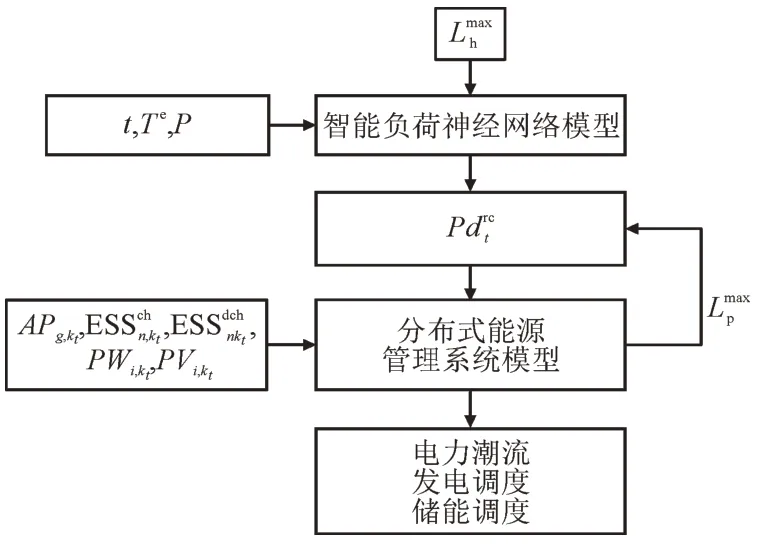
图3 模型求解流程Fig.3 Model solving process
首先,基于智能电表的测量数据及实际EHMS的仿真数据训练神经网络,得到智能负荷神经网络模型,即住宅可控有功功率关于时间t、环境温度Te、电价P及需求响应控制信号Lmax的函数;其次,将该函数代入分布式能源管理系统模型中,优化得到Lmax的值;将Lmax,t,Te,P代入智能负荷神经网络模型中,计算得到的值;最后,将,等参数代入分布式能源管理系统模型中进行优化,得到DES 的调控策略。
4 算例分析
4.1 基础数据
本文采用IEEE-6 节点[26]系统验证分布式能源管理系统模型的适用性,如图4 所示。
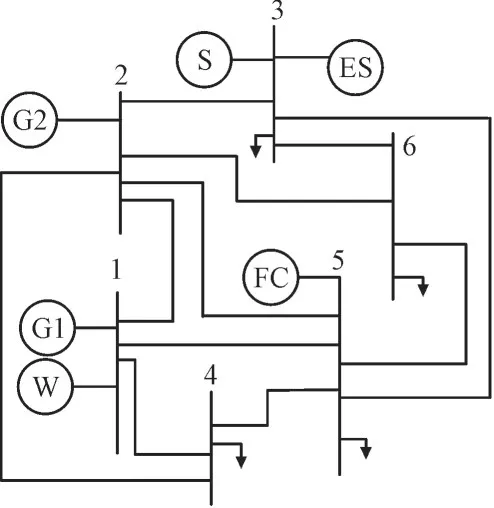
图4 IEEE-6节点测试系统Fig.4 IEEE 6-node test system
该6 节点系统包含6 个电源及4 个负荷节点,其中,G1,G2 为传统分布式电源,S 为分布式光伏,W 为分布式风电,FC 为燃料电池,ES 为储能电池。分布式能源管理系统的各种设备参数如表1 所示。
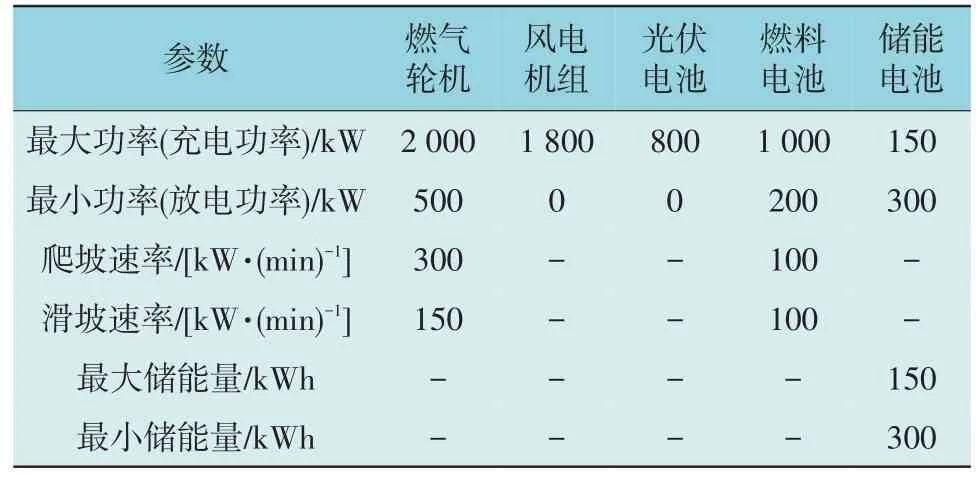
表1 分布式能源管理系统设备参数Table 1 Device parameters of distributed energy management system
相关价格数据根据文献[16]确定。在本算例中,成本函数的二次项ag为0.000 4$/kW2h,一次项bg为13.5 $/ kWh,常数项cg为176.9 $[27];切负荷成本为7.44$/kWh,发电机组启动成本为800$/次,停运成本为400$/次,机组最小启动和停止时间均为6 h,储能系统额定容量为800 kWh,充电效率为0.95,从主网购电的最大值为4 000 kW,最小值为0 kW。
风力发电和光伏发电的典型日出力特性曲线参考文献[28-30],DES 向主网购电的电价曲线如图5 所示。
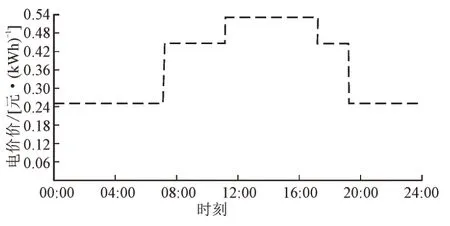
图5 主网购电电价Fig.5 Electricity purchase price for main network
4.2 算例结果
采用MATLAB_R2016b 进行编程计算,并调用求解器DICOPT 对所提模型进行求解,测试平台环境为Intel(R)Core(TM)i7-6700 CPU @ 3.40 GHz,8GB RAM 和Windows 10 专业版系统。
为研究智能负荷需求响应控制信号对DES 运行的影响,本文设置了5 个不同的场景,其可控负荷分别为0,20%,40%,60%及100%,可控负荷的百分比由最优Lmax控制,结果如表2 所示。
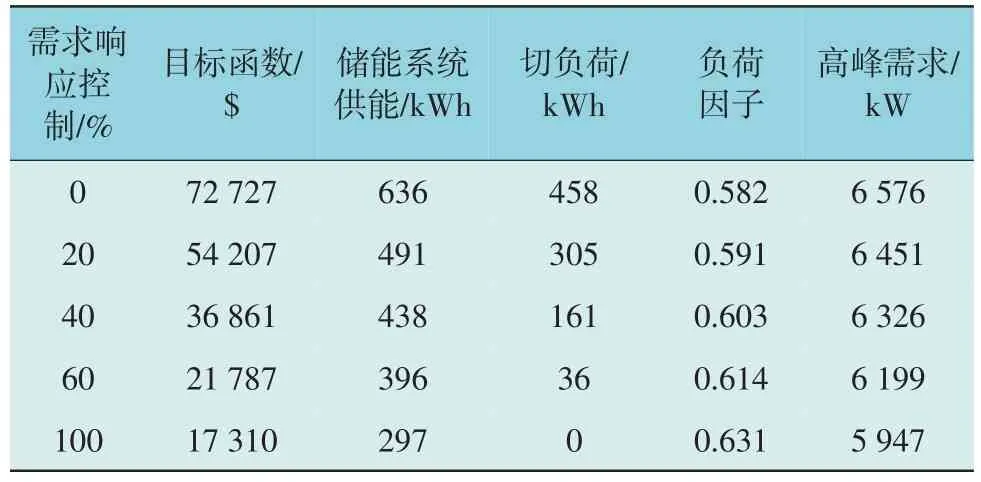
表2 分布式能源管理系统运行结果Table 2 Operation results of distributed energy management system
由表2 可知,随着需求响应控制的加强,系统切负荷不断降低,DES 总运行成本随着需求响应控制的加强而降低。此外,随着需求响应控制百分比的提升负荷因子不断提高,高峰需求也从6.5 MW降低到了5.9 MW。
为进一步分析考虑智能负荷情况对DES 各设备运行的影响,分别对是否含有智能负荷灵活互动的运行调度方案进行对比分析,智能负荷控制比例选择40%。分布式能源管理系统中各个设备出力情况如图6 所示。
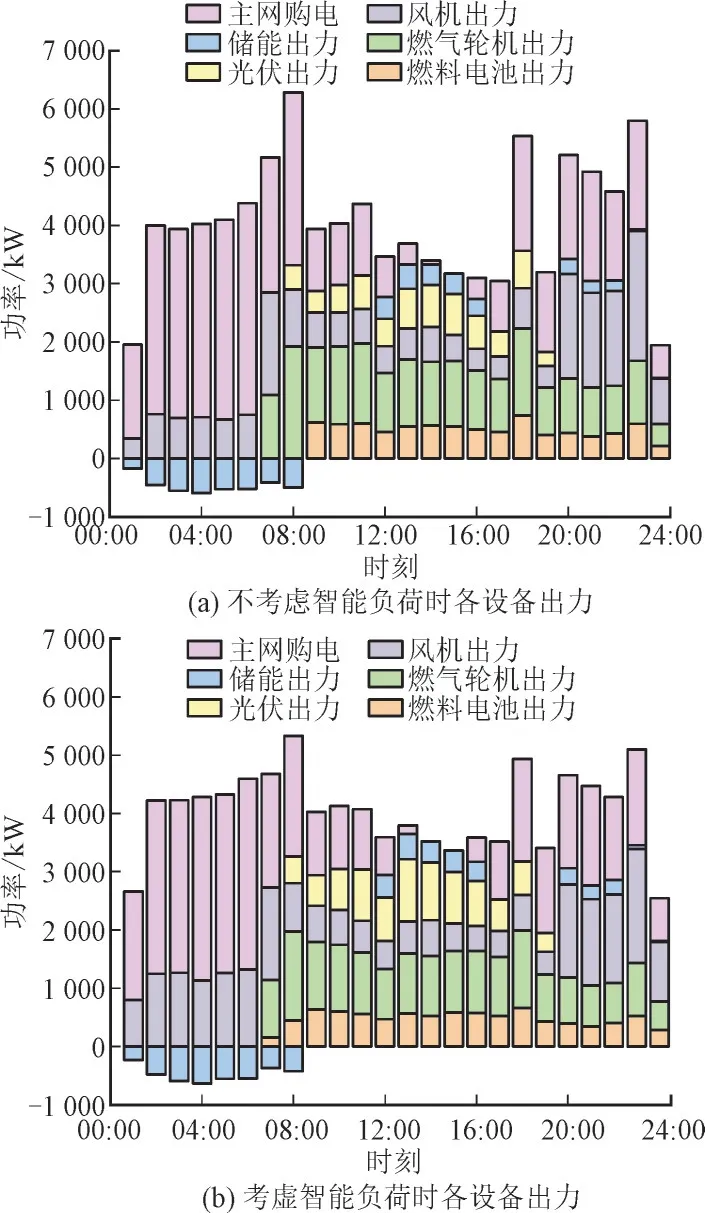
图6 优化前后各分布式能源出力Fig.6 Distributed energy output before and after optimization
从图6 可以看出,智能负荷参与DES 需求响应后,高峰时段负荷相较于未考虑负荷调控时显著降低,分布式能源出力更加平缓。通过调节智能负荷,0:00—7:00 时间段内负荷有所上升,风力发电的消纳量得到提升,可有效减少弃风现象。在9:00—16:00 时段内,考虑智能负荷调度及管理系统的调控策略,可提高低谷时期负荷量,在不增加主网购电情况下促进光伏发电的消纳。由图7 中考虑智能负荷调控前后对比可知,在考虑对智能负荷调控后,主网购电量有所下降,光伏和风电机组出力有较为明显增加,这是因为智能负荷中的可转移负荷从用电高峰时段转移至用电较少的低谷时段,既缓解了DES 的供电压力,又可最大程度地减少切负荷现象的出现。
图7 为本文仿真6 节点系统考虑智能负荷灵活调控前后实际负荷曲线与负荷需求曲线。图7(a)由于DES 从相连主网购买电量存在容量限制,且考虑整个DES 的最优运行及相应设备机组的启停及爬坡约束,该系统在6:00—8:00,19:00—24:00 2 个时间段中,产生了切负荷现象;图7(b)为考虑对智能负荷进行需求响应合理调控时,分布式能源管理系统能够控制负荷需求,在负荷高峰时,将总负荷中的智能负荷进行时间转移,高峰负荷需求降低,进而降低了切负荷。

图7 IEEE-6节点系统负荷曲线Fig.7 IEEE 6-node system load curves
5 结语
本文将可控有功功率表示为环境温度、电价、时间及需求限制的函数,并构建神经网络模型对其求解。同时,在考虑机组运行约束和网络潮流约束的基础上,构建了分布式能源管理系统模型。此外,本文引入模型预测控制方法以减小可再生能源及电力需求的误差。分析算例结果可以发现,智能负荷参与需求响应在减少用电高峰、减少切负荷、降低总成本及提高负荷因子等方面有积极作用,无需大规模投资便可提高分布式系统的负载能力。
