基于类电磁机制算法的综合能源系统多目标优化调度

冉华军，祝 杰，张 涛

（三峡大学电气与新能源学院，湖北宜昌 443002）

0 引言

为了应对能源危机，全球大力推进能源互联网的发展，各能源之间的关联性和互补性日益加深，采用什么方法方式来提高综合能源的利用效率、减小系统的碳排放量和节减系统的运行成本已成为综合能源系统需要着重考虑的问题[1]。包含风电机组、热电联供（Combined Heating and Power System，CHP）系统、储能设备以及其他供能机组的综合能源系统（Integrated Energy System，IES）打破了以往传统能源独立运行和规划的模式，实现多种能源之间相互协同、耦合互补将成为未来人类社会能源发展的必经之路[2-3]。因此，在能源的生产、转换和使用的过程中，综合能源系统的优化调度以及经济性运行受到了国内外专家学者的重视。

随着国家碳中和目标的提出，综合能源系统的低碳经济性研究受到了广泛研究，文献[4]建立了考虑碳交易成本的综合能源系统经济调度模型，采用了布谷鸟算法进行求解，仿真结果验证了模型在降低系统碳排放量方面的优势。文献[5]提出了考虑柔性负荷和碳交易机制的综合能源系统优化调度模型，通过引入排放罚金机制促进了系统的节能减排。文献[6]将碳交易机制引入综合能源系统，通过划分碳排放量区间来构造阶梯型综合能源系统调度模型，兼顾了系统低碳性与经济性。但上述文献多为单目标优化或将多目标加权转化为单目标，得到的最优策略较为单一，无法对运行经济性与低碳性进行灵活地调控。因此多目标优化算法在IES 调度问题中得到了推广应用，文献[7]提出了一种考虑随机性的综合能源系统多目标日前调度方法，以最小化运行成本和污染气体排放量为目标，采用了NSGA-II 算法求解得到一系列调度方案，实现了系统的经济环保运行。文献[8]考虑分时电价对冷热电联供系统的影响，以经济成本和环境成本为优化目标，根据求解得到的pareto 最优解，验证了所提模型的节能减排优势。然而传统的多目标优化算法在约束较复杂的调度问题中易陷入局部最优，算法的性能仍有待提升。

电转气（Power to Gas，P2G）设备作为电-气耦合设备，可在低谷时段将难以消纳的弃风功率转换为易于存储的天然气，实现电-气网络的深度耦合[9]。文献[10]提出了考虑需求响应的含P2G 电-气综合能源系统优化调度模型，并采用机会约束对模型不确定性进行处理。文献[11]在考虑P2G 设备运行成本的基础上，提出了一种计及分段弃风成本的多能源优化运行模型，分析了P2G 在提升风电利用效率和减少系统供能成本方面的突出优势。但有关P2G在系统低碳调度中的研究仍较为欠缺，其P2G 的碳减排潜力仍有待挖掘[12]。

本文以综合能源系统为研究对象，将系统运行成本与碳排放量作为优化目标，考虑P2G 在节能减排方面的作用，建立综合能源系统多目标优化调度模型。本文先分析了传统类电磁机制算法（Electromagnetism-like Mechanism，ELM）的优缺点再进行改进，模型的求解采用改进的类电磁机制算法（Improved Electromagnetism-like Mechanism，IELM），通过仿真结果验证了模型与改进算法的适用性与有效性，调度结果表明P2G 设备能有效提升系统弃风消纳水平和低碳经济性。

1 IES多能耦合设备数学模型

本文所提的IES 的基本结构如图1 所示，其中参与系统调度的设备包括风电机组、热电联产机组、P2G、燃料电池和燃气锅炉和蓄电池[13]。系统的电负荷主要由上级电网、风电机组、热电联产机组和蓄电池提供，热负荷则是由燃气锅炉和热电联产机组提供，P2G 作为电-气耦合设备，消耗系统中的电能产生天然气为耗气机组提供燃料。

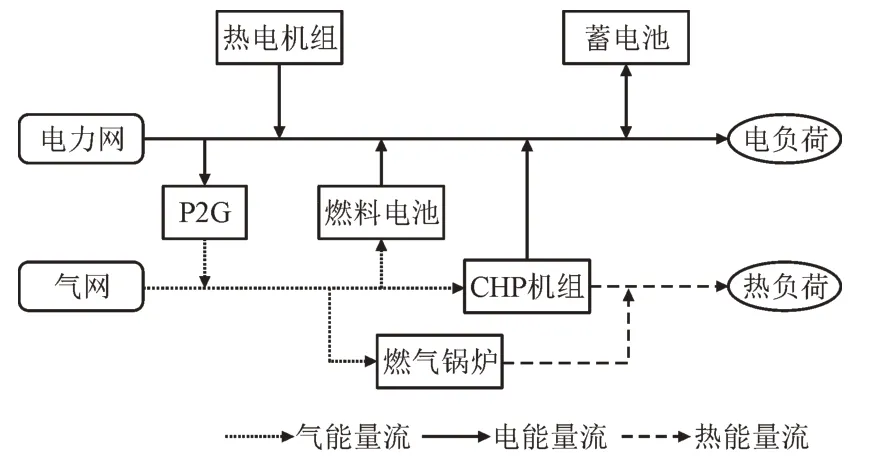
图1 综合能源系统基本结构Fig.1 Structure of integrated energy system

1.1 热电联产机组模型

热电联产机组（Combined Heat and Power，CHP）通过消耗天然气产生电能和热能，其电热出力关系如式（1）所示：

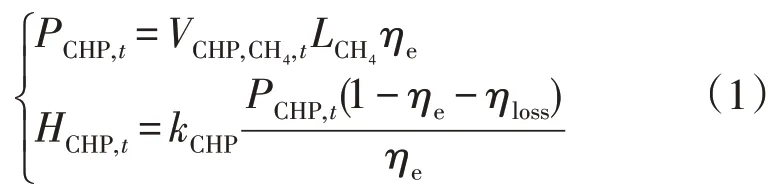
式中：PCHP,t和HCHP,t分别为t时段CHP 机组的电功率和热功率；kCHP为CHP 机组的热电比；ηe为CHP机组的发电效率；ηloss为CHP 机组的热损耗率；为天然气的低热值[14]；为t时段CHP 机组的耗气量。

1.2 燃气锅炉模型

燃气锅炉（Gas Boiler，GB）通过燃烧天然气为系统提供热能，其数学模型可描述为：

式中：HGB,t为t时段GB 的热功率；为t时段GB 的耗气量；ηGB为GB 的制热效率。

1.3 燃料电池模型

燃料电池（Fuel Cell，FC）为气-电转换设备，其产能的耗气量表达式为：

式中：PFC,t为t时段FC 的热功率；为t时段FC 的耗气量；ηFC为FC 的发电效率。

1.4 P2G模型

P2G 装置主要包含2 个化学过程：（1）将水电解成氢气和氧气；（2）二氧化碳和氢气在高温高压的环境下产生甲烷。

P2G 耗碳量的表达式为：

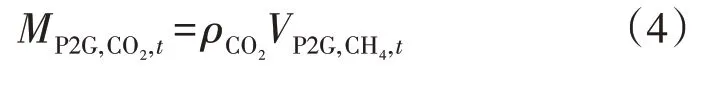
P2G 甲烷产气量的表达式为：

P2G 可利用自身的灵活出力特性实现弃风功率的消纳[15]，其弃风消纳量的表达式为：

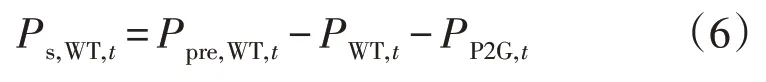
式中：Ps,WT,t为t时段的弃风消纳量；Ppre,WT,t为t时段风电预测功率；PWT,t为t时段风电实际出力。

2 考虑经济性与低碳性的IES多目标优化模型

2.1 目标函数

2.1.1 经济性指标

经济性指标以总运行成本F1最小化，包括运维成本、燃料成本、交互成本和购碳成本，其计算式如下：

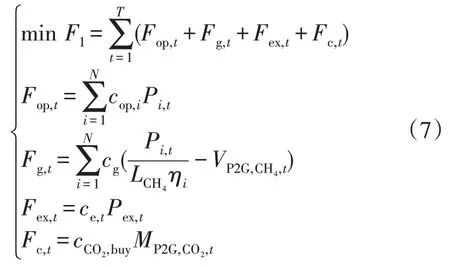
式中：Fop,t为t时段总运维成本；Fg,t为t时段总燃料成本；Fex,t为t时段总交互成本；Fc,t为t时段的购碳成本；T为总调度周期；N为常规机组的类型数；cop,i为第i种常规供能设备的运维成本；Pi,t为第i种常规供能设备的出力；cg为天然气单价；ce,t分别为t时段电价；Pex,t分别t时段的电交互功率；为购碳价格。

2.1.2 环保性指标

环保性指标为碳排放量总量最小化，包括从主电网购电时的碳排放量和设备运行产生的碳排放量，其计算如下：

2.2 约束条件

2.2.1 常规机组运行约束

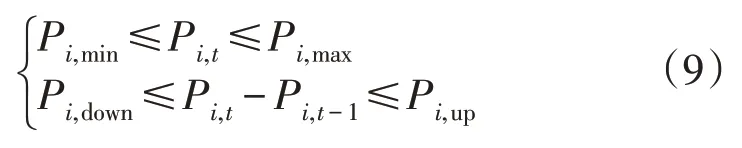
式中：Pi,max和Pi,min分别为第i种常规供能设备的出力上、下限；Pi,down和Pi,up分别为第i种常规供能设备的下爬坡速率和上爬坡速率。

2.2.2 功率交互约束

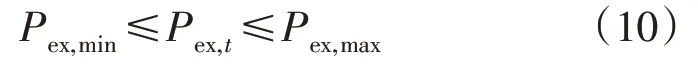
式中：Pex,max和Pex,min分别为电交互功率的上、下限。

2.2.3 功率平衡约束

IES 运行需满足供需匹配约束的表达式如下：

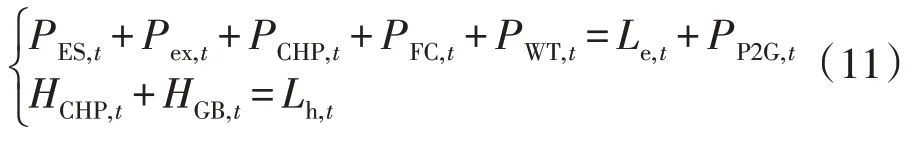
式中：PES,t为t时段ES 的出力；Le,t和Lh,t分别为t时段的电、热负荷。

2.2.4 蓄电池（energy storage，ES）运行约束

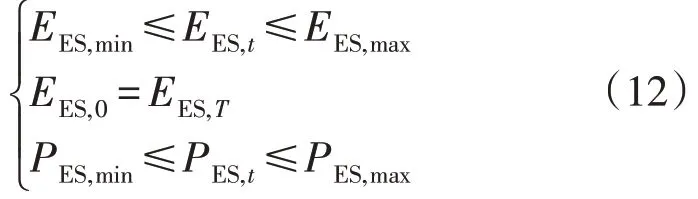
式中：EES,t为t时段ES 的容量；EES,min和EES,max分别ES 的下、上限约束容量；PES,min和PES,max为ES的充放电功率的下、上限；EES,0和EES,T分别为ES在调度周期起始时刻和结束时刻的容量。

3 IELM算法

3.1 基本ELM

ELM 算法的基本寻优公式如下[17-19]:

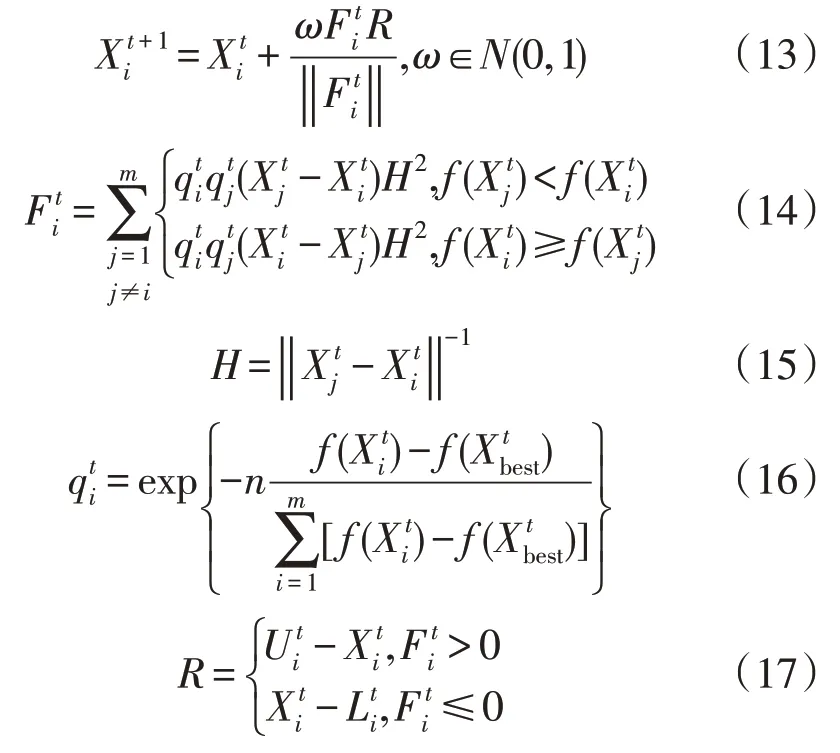
式中：ω为移动步长，是（0，1）之间的随机数；H为空间中两个电荷之间的距离；m为种群粒子总数；n为粒子维度；为第t次迭代中的第i个粒子；为第t 次迭代中适应度值最好的粒子；为第t次迭代中的第j个粒子的电荷量；f(·)为粒子的适应度值；‖ ‖· 为向量的2 范数；为第t次迭代中的第i个粒子的总矢量力；R为种群越界搜索约束；和分别为的上下限。

ELM 算法结构简单，当用其求解函数的全局最优值时，无论是简单的函数表达式还是复杂高维的函数，ELM 算法都可以得到应用。但是经典ELM算法仍然存在以下不足：（1）初始种群是随机产生的，不均匀的种群分布会影响搜索性能；（2）随机线性搜索算法作为局部搜索策略过于简单，算法容易陷入局部最优，使得算法不能得到真正的解；（3）粒子更新规则太简单，可能更新后的粒子反而更差，影响算法的求解精度和收敛性。

因此需要继续对ELM 算法进行研究和改进，优化算法的性能，使其在解决综合能源系统优化调度问题时具有更好的高效性和稳定性。

3.2 改进的多目标类电磁机制算法

3.2.1 基于立方混沌映射的种群初始化

对于基本ELM 算法而言，初始种群的随机性大，与最优解往往相差甚远，严重影响了迭代搜索的效率。为提升种群多样性和遍历均匀性，引入立方混沌映射在搜索空间内动态、均匀地生成初始种群[20]。立方映射的表达式为：

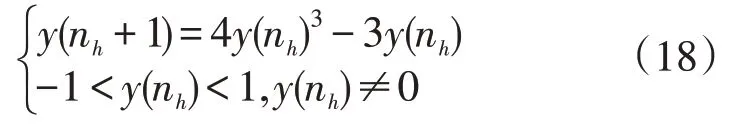
式中：nh为混沌迭代次数。

3.2.2 引入差分算法中的交叉变异

为解决ELM 容易陷入局部最优解的问题，引入差分算法中的变异和交叉策略[21]，粒子在更新位置时出现的自然阻碍，对ELM 中的粒子位置更新进行处理，平衡全局搜索能力。具体操作如下：

1）在第t次迭代中，从种群全部个体中随机选择3 个不同个体，变异策略为：

式中：F为缩放因子，用于增大或减小差分向量的影响力；p1，p2，p3 为同一代粒子的不同标记号。

2）为了丰富种群的多样性，采用交叉操作来实现，即：

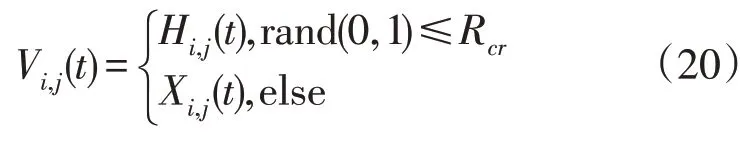
式中：Rcr为交叉概率。

3.2.3 引入自适应权重因子

权重因子的随机性会致使算法在后期迭代时不收敛。为协调算法的全局和局部搜索，提高其的收敛性能，令ω自适应控制函数为：

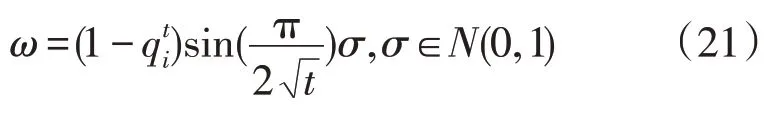
式中：σ为随机系数。

3.2.4 多目标函数的处理

为求解本文所提多目标函数的优化配置模型，在以下2 个方面对基本ELM 算法进行改进：

1）引入NSGA-II 算法中的快速非支配排序、拥挤度计算和精英保留策略。具体原理可见文献[22-24]。

2）采用模糊隶属度法选择综合满意度最高的解。

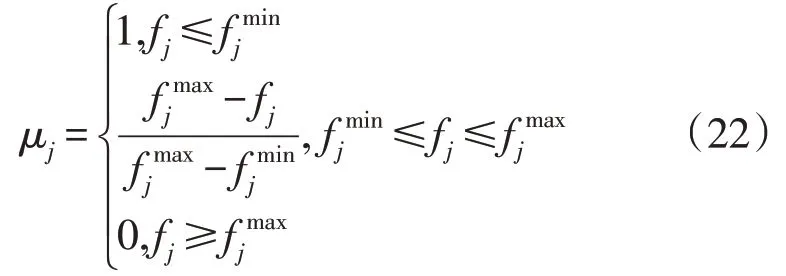
式中：fj为第j个目标函数值；分别为第j个目标函数的最小值和最大值。

根据式（23）计算pareto 最优解集中各个解的综合满意度S，并选取综合满意度最大的解作为最优折衷解。

式中：S为解的综合满意度；μj为第j个目标函数。

4 算例分析

以北方某小型综合能源系统为例，系统的基本结构如图1 所示，风电及电热负荷的预测数据如图2 所示，各设备的参数如表1 所示，系统购售电数据如表2 所示，天然气价格为2 元/m3；天然气低热值为9.7 kWh/m3。

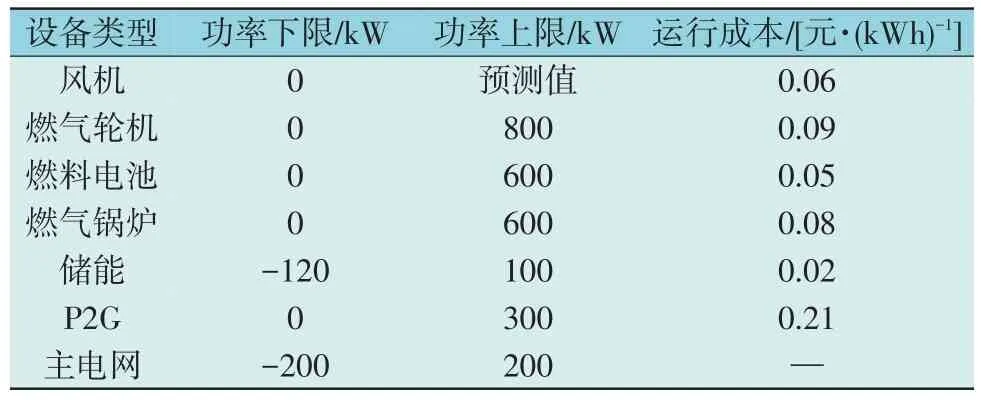
表1 各设备运行成本Table 1 Operating cost of each equipment

表2 分时购售电电价Table 2 Time-of-use power purchasing and selling price

图2 风电出力和电热负荷分时预测图Fig.2 Forecasting of wind power output，electric load and thermal load of each time period

4.1 算法对比

算法pareto 前沿对比如图3 所示，传统ELM 算法由于粒子移动规则较为单一，在搜索过程中陷入了局部最优，导致其前沿解十分集中，求解结果不能兼顾两个目标函数。NSGA-Ⅱ算法则通过非支配排序和精英保留策略有效的平衡了多个目标之间的关其pareto 前沿分布较为分散，而改进EIM 算法通过对传统ELM 算法的初始种群设置和粒子更新进行改进，得到更加均匀的Pareto 前沿，算法的收敛性和求解精度明显提升，验证了本文所提算法的有效性与优越性。

图3 各算法的Pareto对比Fig.3 Comparison of Pareto among algorithms

由表3 求解结果可知，3 种算法的折衷解中IELM 算法的运行成本最低，并且其碳排放量介于ELM 算法与NSGA-II 算法之间。由于ELM 算法所得解陷入了局部最优，其结果无实际应用价值，因此可看出IELM 算法对优化结果具有较好地提升。

表3 各算法求解结果对比Table 3 Comparison of solution result among algorithms

采用IELM 算法和NSGA-II 算法求得的总运行费用和碳排放量结果如图4、图5 所示。

图4 2种算法总运行费用对比Fig.4 Comparison of total operating costs between two algorithms

图5 2种算法碳排放量对比Fig.5 Comparison of carbon emissions between two algorithms

为验证IELM 算法的性能以及Pareto 解的最优性，本文将IELM 以及NSGA-Ⅱ独立运行50 次，对不同的目标函数可得到50 个外部解。根据图4、图5 提供的数据位置和分散情况进行分析，进而判断不同算法的性能与Pareto 解的最优性。根据图4、图5 的绘图方法，箱体越小表明数据越集中即算法稳定性越高；箱体中部的黑色粗线代表结果的均值。

由图4 和图5 可以看出，IELM 算法的数据分布明显小于NSGA-II 算法，因此算法求解结果的稳定性在改进后得到了有效提升。与此同时，在求解结果的均值方面，2 种算法在总运行费用方面接近，而IELM 在碳排放量上明显低于NSGA-II 算法，由此可见IELM 算法在解的整体精度上要优于传统NSGA-II 算法。

为验证前文所引入的立方混沌映射、差分交叉变异和自适应权重对算法求解性能的影响，表4—表7 给出了3 种改进方法对算法指标影响的相关对比结果。每组结果基于算法50 次运行结果取平均值得到，表4 中最优初始解的适应度平均值指50次运行下的算法初始化种群的最优折衷解的平均适应度值，包括总运行成本和碳排放量2 个目标值，最优适应度平均值指50 次运行情况下的最优折衷解的平均适应度值，包括总运行成本和碳排放量2 个目标值，表6 中种群熵的计算方法可见文献[25]，种群熵值一般处于0.9-1，值越接近1 说明种群多样性越差，表明算法陷入了局部最优。

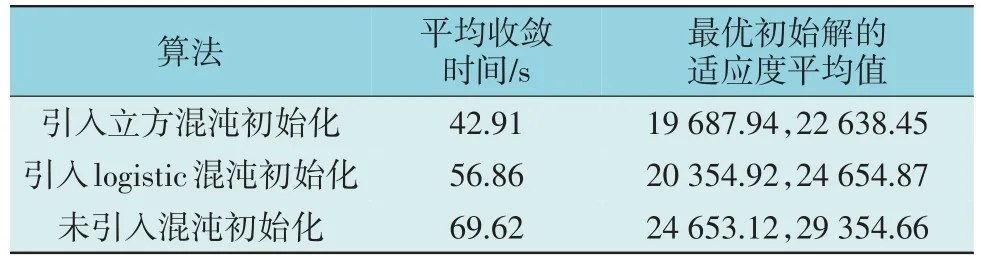
表4 混沌初始化对算法性能的影响Table 4 Influence of chaos initialization on algorithm performance

表5 差分交叉变异对算法性能的影响Table 5 Influence of differential crossover mutation on algorithm performance

表6 自适应权重对算法性能的影响Table 6 Influence of adaptive weight on algorithm performance

从表4 可知，未引入混沌初始化的IELM 算法的初始解的位置和求解速度最差，现有大多数文献采用的logistic 混沌初始化对算法初始解的生成和算法求解时间具有一定的积极作用，而本文所提的立方混沌映射初始化对两种指标的积极影响较传统logistic 映射方法得到了进一步加强。从表5 可知差分交叉变异的引入提升算法的求解精度，但交叉变异过程牺牲了一定的求解时间。从表6 可知，自适应权重的引入有效提升算法的求解速度，与此同时种群熵得到了降低，提升了种群的多样性，有效避免了算法陷入最优解。综合来看，引入的改进算法分别对算法初始化位置、求解速度、求解精度和种群多样性多个方面进行了优化，且3 种改进方法在求解时间方面具有一定互补性，求解结果可以验证本文所提改进方法的有效性。

4.2 IES调度情况

为了对比P2G 在降低系统运行成本与碳排放量方面的优势，本文设置了2 种对比情景：情景1：在系统经济调度中考虑P2G；情景2：在系统经济调度中不考虑P2G。并对两种情景进行求解，结果如表7 所示。

表7 各情景下求解结果对比Table 7 Comparison of solution result under different scenarios

2 种情景下的各时刻购气量如图6 所示。

图6 各时刻购气量对比Fig.6 Comparison of gas purchasing of each time period

根据图6 的求解结果可知，情景1 的总运行成本和碳排放量都低于情景2，说明P2G 装置对于降低系统运行成本于碳排放量具有积极意义。这是由于P2G 装置可将部分碳排放的CO2与水通过甲烷化反应制造甲烷，再供给燃气使用设备，从而降低了系统购气量。这一方面降低了系统的总运行成本，另一方面也使得机组的运行更加合理，从而降低了系统碳排放。

2 种情景下的各时刻弃风消纳量如图7 所示。

图7 各时刻弃风消纳量对比Fig.7 Comparison of integration of curtailed wind power of each time period

由图7 可看出加入P2G 装置后系统风电消纳情况明显得到改善。P2G 装置可利用弃风功率电解水产生氢气，氢气和二氧化碳在高温高压下产生甲烷，提供给燃气系统，从而提升了系统风电消纳率。

在情景1 下的各时刻运行成本和碳排放量如图8 所示。

图8 情景1的各时刻运行成本和碳排放量Fig.8 Operating costs and carbon emissions of each time period in scenario 1

从图8 可看出碳排放量在夜间18～24 h 较大，零点之后碳排放量逐渐减小。碳排放量主要来自于燃气机组，由于受系统“以热定电”的影响，碳排放量的变化趋势大致与热负荷功率变化情况接近。由于P2G 设备与风电机组参与供电，系统总运行成本则与电功率的变化趋势接近。

5 结论

本文针对综合能源系统节能减排问题，引入P2G 设备促进系统消纳弃风和实现碳减排，构建了考虑经济性与低碳性的IES 多目标优化调度模型，并采用改进的类电磁机制算法对模型进行求解，仿真结果表明：P2G 设备能有效降低系统购气量，并且对于系统的弃风消纳具有积极作用；改进的类电磁机制算法在求解精度和算法稳定性上都优于传统的多目标算法。

本文所提出的IES 调度模型尚未考虑电-气-热网络的能量流失及动态特性，后续会研究设备和网络的动态运行模型，构建合理的能源损耗评估指标，制定更加精确调度策略。