基于PSO-Soft attention双向LSTM算法的光伏发电量预测研究

赵晋斌，张建平，，毛 玲，屈克庆，黄成建，揭业炜

（1.上海电力大学电气工程学院，上海 200090；2.国网嘉兴供电公司，浙江嘉兴 314000）

0 引言

伴随全球能源形势日益紧张，常规能源的开发与利用被不断制约，太阳能因其具有储量丰富、清洁无污染等优点，被公认为是新能源发电的理想来源之一[1]。光伏发电作为太阳能利用的重要方式之一，被社会各界广泛关注[2]，考虑到光伏发电方式受多种气象因素的影响，其功率波动性高的特点将影响大范围光伏发电系统的安全[3]。2021 年6 月11日，国家发改委发布《国家发展改革委关于2021 年新能源上网电价政策有关事项的通知》（发改价格[2021]833 号），2021 年新能源新建项目可自愿通过参与市场化交易形成上网电价。

目前光伏发电的预测模型主要为统计模型[4]，方鹏等人采用了长短时记忆（Long Short-Term Memory，LSTM）神经网络的中长期光伏电站发电量预测模型[5]，实验数据集使用了光伏发电站的长期历史发电量以及电站周围光照强度等数据，由于LSTM 算法的细胞单元的记忆能力有限，在中期数据具有较好的应用，目前较难解决长期数据问题。翟载腾等人提取了光伏发电组件的实际运行参数，同时根据这些参数的大小建立了实际工作环境中的电池输出特性方程，并求解特性方程从而得到预测功率值[6]。杨朋等人指出了其光伏电池输出功率与温度和光照强度的关系，其通过二维表预测出了光伏电池输出功率，将功率预测转化为温度和光照强度的预测，该方法能够比较准确地预测出光伏电池的最大输出功率，但是光照强度和温度较难实时获取[7]。陈昌松等人考虑到了主要影响光伏发电的输出功率的核心影响因素，采用光伏阵列的发电量数据、光照强度和环境温度等特征建立了误差反向传播（Back Propagation，BP）神经网络预测模型。但是由于BP 神经网络本身就存在容易陷入局部最优值、较难收敛等一系列缺点，该方法需要大量发电站的历史数据支持，计算量相当大[8]。Mellit A 等人采用了不同小时的天气信息实测数据作为预测输入的日类型信息，用这些数据求解光伏发电系统的输出功率，存在预测时间较短的问题[9]。

本文采集杭州山都光伏发电站的部分机组发电量历史数据，并整理得到多类不同特征的气象数据集合，传统神经网络存在泛化性能差以及易进入局部收敛等问题[10]，同时光照强度、环境温度等多种因素都会对太阳能发电的输出功率产生影响[11]。在光伏电厂发电量预测中，本文提出的PSO-Soft attention 双向LSTM 算法结合了深度学习双向LSTM网络的改进方法预测发电量，该方法不仅具有传统LSTM 的时序建模能力[12]，而且还能后向推算数据，具备时空特性。本文主要改进了PSO-Soft attention双向LSTM 算法的前后向传播部分，前向传播过程中通过自适应学习策略的粒子群优化算法（Particle Swarm Optimization，PSO）对LSTM 模型的关键参数进行寻优，在网络的主体部分重新调整网络为八层网络结构并在前向传播部分加入了两层卷积层，反向传播部分加入了Soft attention 机制，增强了其网络的稳定性，相较于传统机器学习算法，该算法在泛化能力、鲁棒性以及运算力上具有明显优势[13]。

1 PSO-Soft attention双向LSTM算法

PSO-Soft attention 双向LSTM 算法即双向LSTM 网络结合PSO-Soft attention 机制，其网络结构更复杂[14]，具有更优的时空特性。该模型为下层输入上层输出的结构，为获得数据的时序关系以及搭建更优的特征方程，该模型的前向传播部分结合多位置卷积处理[15]，成功实现了卷积层处理中网络状态之间的快速切换并且可获得高维时空特征，同时使用PSO 算法进行模型的前向网络的参数调优，调整了模型的输入参数，PSO-Soft attention 双向LSTM 算法的结构见图1。

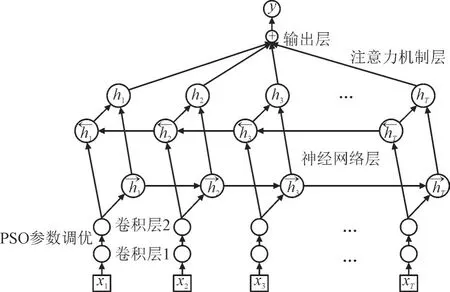
图1 PSO-Soft attention双向LSTM算法的结构图Fig.1 Structure of PSO-Soft attention bidirectional LSTM algorithm

图1 中，x1...xT为输入数据，h1...hT为隐含层，输入的数据经过2 层卷积并且经过PSO 参数调优后，将数据传入隐含层并在双向LSTM 网络中进行传递，最后通过注意力机制增强其数据稳定性，最终输出模型预测结果，其中算法训练过程的伪代码如下：

其中Xtest为输入的测试集数据，Xtrain为输入的训练集数据，dij为输入信息xi和xj之间欧氏距离，dc为截断距离；对于局部密度ρid最大的样本，其δid=maxj(dij)，该值为样本空间距离的最大值，若xi的密度是最大局部密度，则δid远大于其最邻近粒子的δid平均距离；yi为发电厂日发电量真实值，模型的输出为发电厂日发电量预测值；c1和c2为粒子权重系数，ω为惯性权重系数；pbestid和gbestcd分别表示某个粒子最好位置第i维的值、整个种群最好位置第i维的值。

伪代码过程解释了PSO-Soft attention 双向LSTM 网络的运行过程，PSO 网络主要通过计算输入特征之间的距离，调整双向LSTM 网络的前向传播部分的参数，使网络具有更好的处理数据的高维特征的能力。

2 数据集以及特征方程

2.1 数据集构建

本文的数据集采用杭州山都光伏发电站K13 号机组从2018 年8 月1 日到2020 年5 月31 日的日发电量数据，在机组中的每个设备采集完成后，将发电量按天整合到一起，发电量的值设置为yN，yN为标签，并结合该发电站所处的位置，在杭州气象局网站提取该区域的日平均温度、节假日、日照强度以及月份等因素，共同作为输入特征，其特征的数值被分别存为(x1i,...,x4i)∈R4*i，表示总量为670 组的该时段发电机组的日发电量数据的特征向量，R4*i为样本数据集合，便于之后的特征方程搭建，并且结合历史的发电数据构造了数据集(x1i,...,x4i,yi)∈R4*i，该类数据的前80%划分为训练集数据，后20%划分为测试集数据。

2.2 特征方程

本文提取的温度特征为该机组该时段中的日平均温度，平均温度是每一天温度的最真实反应，太阳能电池板的能量转换效率会随着温度变化而不同，故不同季节的平均温度会影响发电量。同时节假日期间的城市用电量下降是导致发电厂发电量下降的另一大重要因素，太阳光在不同时间下的光照度不同，而日照强度的大小将决定光伏发电厂的发电量，故该指标为核心影响因素之一。由于光伏发电具有一定季节性，故不同月份的发电量也差异明显，分别将这4 类特征放入本文数据集中的前4 列中，并采用了Polynomial Features 方程构造特征方程，该4 类特征将作为算法预测的重要依据之一[16]，Polynomial Features 方程为：

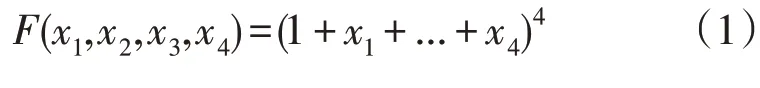
3 算法预测过程

3.1 输入数据介绍

本文所用的模型输入为2 部分：

1）第一部分为(x1i,...,x4i,yi)，其中x1i,...,x4i为输入的特征向量，670 为输入的样本数量，以上数据为历史数据集。

将(x1i,...,x4i,yi)和(x1i,...,x4i)∈R4*i作为输入部分，放入模型中进行训练，模型最终按天输出未来120 天的日发电量，预测流程的结构如图2所示。

图2 预测流程图Fig.2 Process of forecasting power generation

3.2 软注意力机制

本文所用的Soft attention 机制的原理如图3 所示。图3 中h1...hN为网络的隐含层信息，αi为隐含层权重，N为输出样本总数，St为输入信息。

图3 Soft attention机制Fig.3 Soft attention mechanism

Soft attention 每次会照顾到全部的位置，故Soft attention 是光滑的且可微的，即双向LSTM 的目标函数对权重αi是可微的，因为目标函数对预测值yt可微，而yt对αi可微，根据链式法则可知目标函数对αi可微[17]。

3.3 PSO机制

现在定义一个群体中含m个颗粒，在t次迭代中，定义第i颗粒子位置与速率依次为Xit和Vit，算法通过监督两个最优解进行位置与速率更新，第1个解即局部最优解pbesti，该解为粒子自身进行计算得到的最优解，第2 个解即全局最优解gbesti，为整个种群体当前计算查找的最优解[18-20]，粒子速率和新位置的更新公式为：

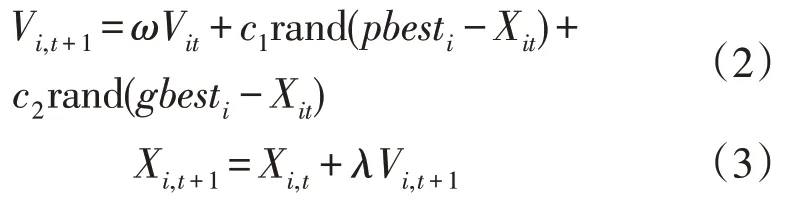
式中：c1和c2为学习因子；rand 为[0，1]之间随机数；λ为速度系数，λ=1。

3.4 PSO-Soft attention 双向LSTM算法门结构运行机制

本文所用的PSO-Soft attention 双向LSTM 算法的结构主要包含遗忘门、输入门、细胞单元更新模块和输出门等，门结构如图4 所示。图4 中ft为遗忘门的函数，it为经过输入门处理的输出也是记忆细胞的权重，Ct-1为t-1 时刻的细胞状态，为细胞单元更新后的细胞状态。ht-1为t-1 时刻的隐含层状态，并且由于网络是双向的，故ht也有方向，前向为，后向为，Xt为t时刻的输入信息，ot为模型输出门对应的输出，σ为sigmoid 激活函数，Tanh为Tanh激活函数。

图4 模型门结构图Fig.4 Door structure of model

3.4.1 遗忘门

新信息的输入需要先进行遗忘的操作，先丢弃旧的信息，该过程通过遗忘门来实现，该门会读取ht-1和Xt，遗忘门表达式如下：

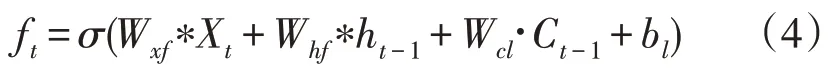
式中：*为叉乘符号；·为点乘符号；ht-1为上一个时刻的隐含层的输出；Wxf，Whf，Wcl分别为变量Xt、变量ht、变量Ct的权重；bl为遗忘门的偏置。

3.4.2 输入门

算法中输入门的作用为生成待更新的数据，输入门的激活函数选用Tanh 函数，输入信息和细胞状态信息通过点乘的形式输入，其输入门的表达式为：

式中：Wxi，Whi，Wci分别为变量Xt、变量ht-1、变量Ct-1的第i个权重；ht-1为第t-1 时刻的隐含层的输入；bi为输入门的偏置；Ct为第t个时刻细胞单元的输出；Wc为统一的细胞单元的权重；bc为该细胞单元所对应的偏置[21]。

3.4.3 细胞单元更新机制

老的细胞层通过乘以ft遗忘不需要的信息，并且与相加，得到候选值时的细胞单元更新公式为：

Ct-1为t-1 时刻的细胞状态，对遗忘门信息点乘之后的结果再和输入门信息累加，最后得出t时刻的细胞状态。

3.4.4 输出门

输出门先通过Sigmoid 激活函数获取模型的初始输出值，随后利用Tanh 层将Ct的值缩放到-1 到1 之间，再将其逐对相乘Sigmoid 激活函数的输出，从而得到该模型的输出，其表达式为：

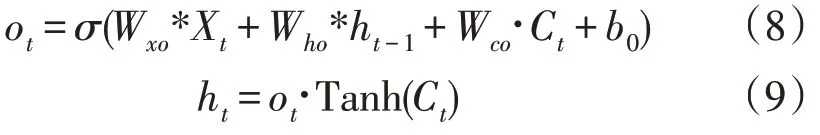
式中：bo为输出门的偏置；Wxo，Who，Wco分别为输入变量Xt，隐含层ht-1，细胞单元Ct的权重系数，其中网络模型的输出定义为0～1，通常以概率值形式存在，Tanh 激活函数会稳定数值，故采用该激活函数进行门结构的激活[22]。

3.5 损失函数

本文中的PSO-Soft attention 双向LSTM 算法的损失函数主要使用均方误差损失函数（Mean Square Error），其表达式为：

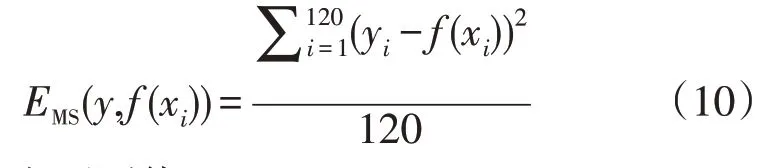
式中：f(xi)为预测值。

PSO-Soft attention 双向LSTM 算法将待预测数据代入该损失函数进行计算，表1 为40 次随机试验下，训练结果的损失函数的4 次最优值[23]（无量纲）。

表1 损失函数最优值Table 1 Optimal value of loss function

4 预测实验

4.1 数据集

本文的数据集采用2.1 节描述的发电量数据，其中部分数据描述如表2 所示。

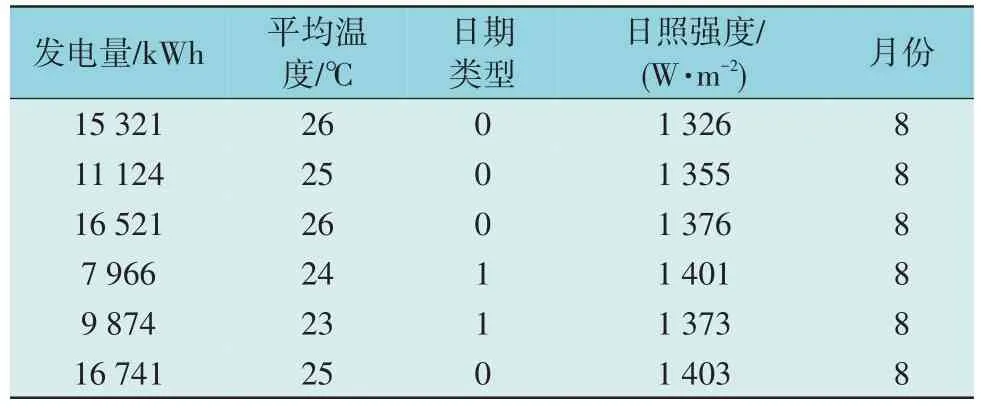
表2 输入的样本数据Table 2 Sample data for input

表2 的数据为输入的样本数据，其中在节假日时特征为1，工作日为0。待预测数据为去除了日发电量的2020 年6—9 月空数据，具体描述见表3。

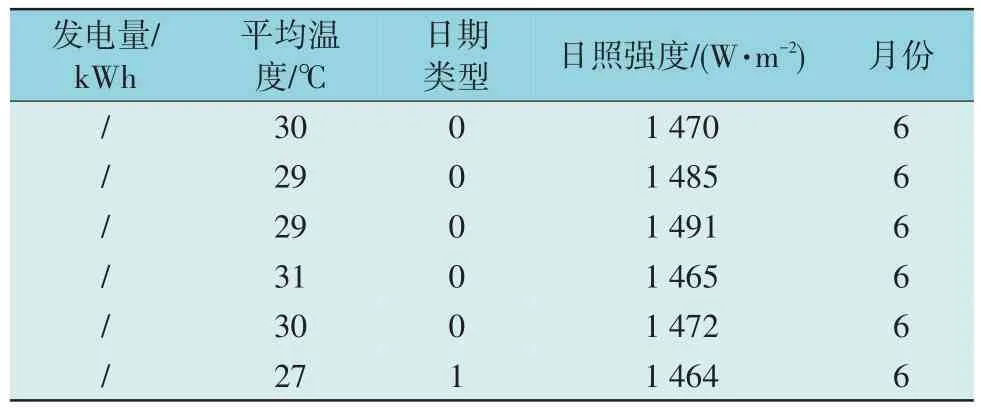
表3 待预测数据Table 3 Data waiting for prediction

表3 的数据为待预测数据，将上述2 类数据放入网络完成训练，获取预测结果，同时在网络模型中输出预测出的数据，输出数据为2020 年6 月1日到2020 年9 月31 日的发电量按天输出预测结果，为了方便描述表4 选取了前6 天的部分预测出的数据。

表4 模型输出数据Table 4 Output data of model

4.2 模型预测结果

在算法的预测实验中，将历史数据对比预测值，如图5 所示，可以准确预测未来120 d 的发电量数据，数据周期性真实历史规律与预测值误差较小，约在5%左右，这说明预测结果达到预期，并且满足实际应用标准[24]。

图5 预测值与真实值对比Fig.5 Comparison between predicted values and real values

4.3 对比实验

在同一个数据集下，采用SVM 算法，LSTM 算法和PSO-Soft attention 双向LSTM 算法同时进行预测[25]，分别用平均误差（Mean Absolute Percentage Error，MAPE）、均方根误差（Root Mean Square Error，RMSE）等两个指标对比三者的泛化性能，两个指标的表达式为：

式中：n为预测的样本总天数。

将SVM，LSTM 以 及PSO-Soft Attention 双 向LSTM 模型预测的6—9 四个月的预测值带入MAPE和RMSE 的指标中，发现PSO-Soft attention 双向LSTM 算法在该两类指标中的性能均优于其他算法，3 个网络的实验结果见表5。

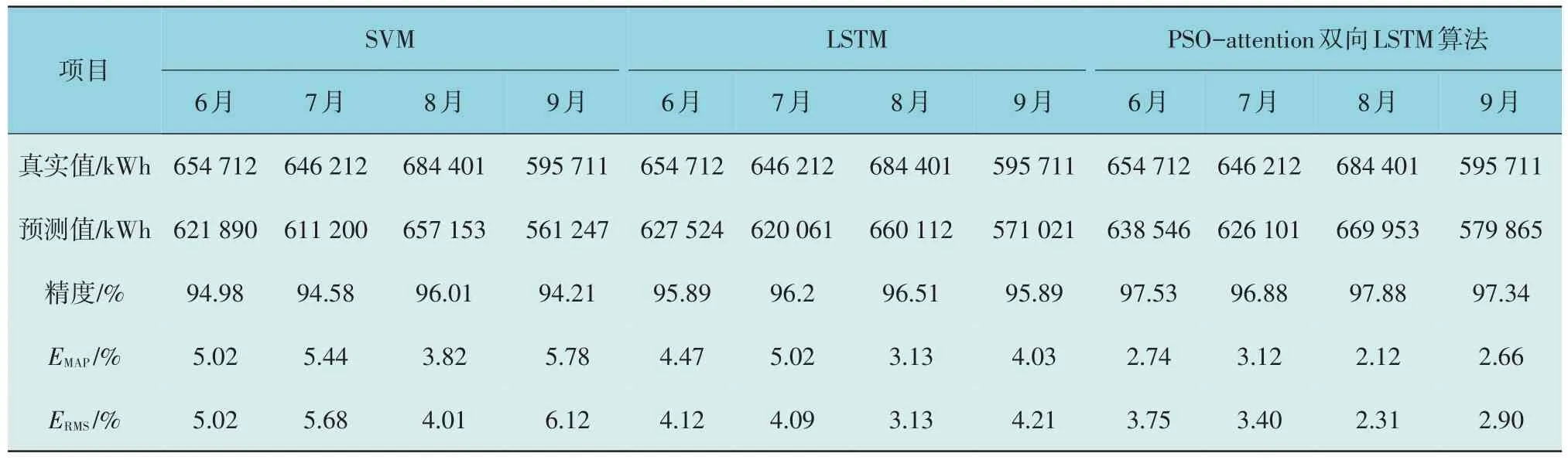
表5 SVM实验结果Table 5 SVM experimental results

图6 为3 类网络在MAPE 指标下的对比结果。由图6 中的对比结果可以看出，本文提出的改进网络由于PSO 算法优化了网络的前向部分参数[26]，故该网络的MAPE 值较SVM 的高2.5%左右，较LSTM 高2%左右。

图6 MAPE对比结果Fig.6 Comparison of MAPE among three networks

图7 为3 类网络在RMSE 指标下的对比结果。从图7 的对比结果可知，由于Soft attention 机制增强了网络的稳定性，该网络的RMSE 值较SVM的高2%左右，较LSTM 高1%左右，所以该网络在预测的准确度上具有一定提升。

图7 RMSE对比结果Fig.7 Comparison of RMSE among three networks

5 结语

本文提出了一种PSO-Soft attention 双向LSTM算法的功率预测模型，该模型不仅具有LSTM 的时序建模能力，同时拥有较好的刻画局部特征的能力[27]。首先解释了PSO-Soft attention 双向LSTM 算法的数学原理以及预测过程，在实验的数据集构建过程中，结合了温度、节假日等特征，构建了可供模型预测的数据集，实验数据集通用性较强，可以结合不同算法进行实验，并在对比实验中采用了MAPE 和RMSE 等指标进行对比，实验表明，本文所用方法比SVM 算法以及LSTM 算法的预测精度高了2%左右。

未来的工作将会在算法层面做出进一步改进，将改进LSTM 网络的门结构部分，使算法具有更高的鲁棒性，同时扩充数据集，调整网络结构，使之实现在大规模数据体量下的发电量预测。