基于扩展卡尔曼滤波的智能电网虚假数据检测

王竞才，李 琰，徐天奇

（云南民族大学云南省高校CPS融合系统重点实验室，云南昆明 650504）

0 引言

智能电网是一种典型的电力信息物理系统（Cyber Physical Power System，CPPS），随着信息网与电网的深度融合，信息网在电力系统的生产调度、运行监控等方面发挥了重要的作用[1-2]，但这也使得CPPS 容易遭受各种恶意网络攻击。在电力应急控制服务的数据传输过程中，对快速响应的需求使得测量设备缺乏抵御恶意信息攻击的能力[3]。近年来多次大停电事件表明一次成功的网络攻击可能导致地区的大面积停电。如2015 年针对乌克兰电网的网络攻击使得乌克兰境内超过10 万户居民停电6 个小时[4]。

在众多的网络攻击中，虚假数据注入攻击是通过控制信息节点，向系统注入虚假数据，达到破坏数据完整性的目的。一次成功的虚假数据注入攻击（False Data Injection Attack，FDIA）可以干扰电力系统的正常状态估计，甚至诱导调度员进行误操作[5]，文献[6]证明了FDIA 可以绕过基于残差的坏数据监测（Bad Data Detection，BDD）。文献[7]构建了基于直流潮流的FDIA 三层攻击模型，验证了FDIA 导致的误操作可能会使电网中的线路过载，但是直流潮流存在误差较大的问题。文献[8]提出了两种交流潮流下的攻击方式，并给出相应防御策略，但在所提及的区间状态估计中由于在一个较高的宽度下进行会导致计算精度不高。FDIA 具有隐蔽性与破坏性，需要对CPPS 进行合理监控和数据检测[9]。

智能电网中广泛应用的状态估计方法是基于加权最小二乘估计（Weighted Least Square，WLS）。目前防范FDIA 有两种方法：基于保护的方法和基于检测的方法，在基于保护的方法中，可以通过向一些重要节点或线路安装抗篡改的测量设备[10-12]或采用先进的加密协议[13-14]等方式，但基于保护的防御方法存在成本较高、对拓扑结构发生变化的电网的适应性较差等问题。而基于检测的方法通常是在状态估计中检测和识别FDIA[15-16]。文献[17]提出一种基于WLS 的递归状态估计，但是WLS 是一种线性估计，用来估计电力系统这个非线性系统还是会有很大误差。文献[18]提出一种基于极端梯度提升结合无迹卡尔曼滤波的电网虚假数据注入攻击检测方法。利用极端梯度提升来预测负荷会使检测更加准确，但仍然面临求解困难的问题。文献[19]提出了一种基于差分序列方差与信息物理系统融合的数字变电站数据异常检测方法，所提方法不仅能有效识别信息设备物理故障和恶意入侵导致的数据异常，对于拒绝服务攻击也能实现准确检测，相比于传统方法具有更高的准确性与可靠性。文献[20]在保留原始WLS 的同时，引入了一个卡尔曼滤波器，通过两估计器的残差来判断系统遭受了攻击，并在滤波过程中加入了一个加权函数，使检测性能大大提升，但也存在着线性滤波的精确度问题。文献[21]提出了一种余弦相似匹配方法，通过比较卡尔曼滤波器的估计状态值和相位测量单元（Phasor Measurement Units，PMU）的测量值来检测FDIA。文献[22]提出一种FDIA 的在线检测方法，利用负荷预测、发电计划和同步相量数据来检测测量异常。文献[23]提出了一种保证全系统可观的相量测量单元优化部署策略。文献[21-23]方法的实现往往依赖于先进的测量设备如PMU 的可靠测量，而如何在极短时间内管理和利用高密度的数据流是一项极具挑战性的任务。

本文提出了一种基于扩展卡尔曼滤波的检测方法，该方法利用检测数据递归得到系统的实时运行数据，是一种递归方法。通过比较WLS 与EKF的残差来实时检测系统数据的准确性。

1 虚假数据注入攻击

攻击者要想发动一次成功的FDIA，首先需要干扰正常的状态估计。式（1）给出了状态估计的量测方程为：

式中：zk为电力系统k时刻的量测量（包括节点注入的有功、无功功率以及线路上流过的有功、无功功率）；xk为电力系统k时刻的状态量（包括节点的电压幅值与相角）；h为状态量与量测量关系的潮流方程；vk为量测误差，满足均值为0 的高斯白噪声，其方差阵为Rk。

在电力系统中，BDD 中大部分的算法通常都是基于残差检验的，将残差rk定义为：

式中：为k时刻的估计状态向量，通常由WLS 求得。

WLS 的具体方法详见文献[8]，通过将残差的二范数与相应阈值τ进行比较来判断是否有坏数据，即：

假设攻击者可以篡改部分节点的量测数据，若攻击者构建的攻击向量满足：

则此时的BDD 结果为：

通过测算工业企业上述各项两化融合评估指标，可对工业企业所处的两化融合发展阶段进行划分，即起步建设、单项覆盖、集成提升和创新突破。从两化融合发展的时间维度来看，单个工业企业将遵循上述四个阶段实现两化融合发展的阶段式跃升。其中，处于起步建设阶段的企业已逐步实现两化融合基础设施配备和环境建设，处于单项覆盖阶段的企业能够将信息技术利用在各单项业务环节中，处于集成提升阶段的企业能够有效实现企业内部各业务环节的综合集成，处于创新突破阶段的企业能够实现跨企业的协同与创新(如图3)。

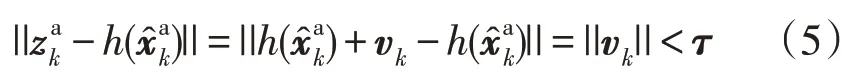
可以看出，FDIA 成功绕过了BDD，关于如何构建的问题在文献[6-8]中已经有了大量的研究，故本文不再讨论FDIA 的实现方法。

2 扩展卡尔曼滤波

卡尔曼滤波的研究对象是一个存在随机性的动态系统，即该系统可以表示为一个随机的，但又有一定运动规律的时间函数。对于电力系统而言，不仅存在式（1）所示的量测方程，还应有体现状态量变化的转移方程，即：

式中：f为状态转移方程；ωk为系统误差，满足均值为0 的高斯白噪声，其方差阵为Wk。

2.1 量测方程

在交流系统中，电力系统状态量与量测量的关系可以分为4 类，即：

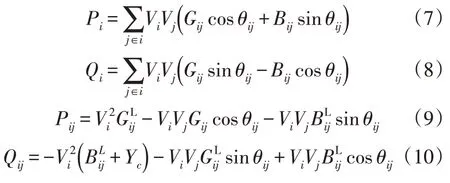
式中：Vi，Vj分别为节点i和j的电压；Pi为节点i注入的有功功率；Qi为节点i注入的无功功率；Pij是线路ij通过的有功功率；Qij为线路ij通过的无功功率；为线路ij的电导；为线路ij的电纳；Yc为线路对地电纳；Gij与Bij分别为导纳矩阵中元素ij的实部与虚部；θij为节点i和节点j的相角差。

2.2 状态转移方程

现代电力系统两次采样的时间间隔都很短[24]，可以认为各节点的有功、无功变化量在两次采样的时间间隔内变化不大，则电力系统的状态转移方程可以从功率方程的增量中导出，即：

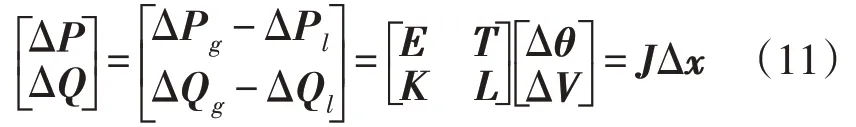
式中：ΔP为总的有功功率增量向量；ΔQ为总的无功功率增量向量；ΔPg为发电机有功变化向量；ΔPl为负荷有功变化向量；ΔQg为发电机无功变化向量；ΔQl为负荷的无功变化向量；Δθ，ΔV为系统有功、无功变化导致的节点电压幅值、相角的变化量向量；J为雅可比矩阵；Δx为状态变量的变化量；E，T，K，L为雅可比矩阵的子矩阵，其元素为，其中，θj为节点j的电压相角，Vj为节点j的电压幅值。

需要注意的是，由于平衡节点的V和θ是固定的，故雅可比矩阵不包括平衡节点的行和列。假设各节点的功率因数tanφ恒定，可以导出，即：

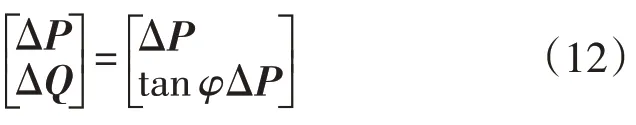
最后，推导出了时变的状态转移函数，即：

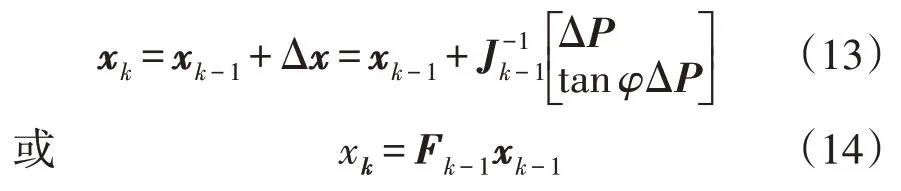
式中：Fk-1=I+A为EKF 的状态转移矩阵，其值为一个单位矩阵I和一个对角矩阵A之和，对角矩阵A中各元素为：

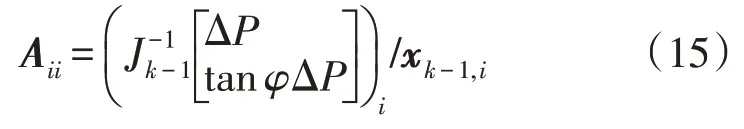
由于状态转移矩阵Fk-1是时变的，可以反映系统中负荷、发电机出力的变化，其精确程度高于恒定的状态转移矩阵。

2.3 扩展卡尔曼滤波算法

卡尔曼滤波的适用场景是线性系统，但是电力系统是一个复杂的非线性系统，因此考虑扩展卡尔曼滤波（Extended Kalman Filter，EKF），EKF 的一般步骤参考文献[25]，对非线性的方程进行泰勒展开，略去二次以上的高阶项，即可得到扩展卡尔曼滤波的形式，分为预测步和滤波步。

1）预测步为：

此外，还应考虑两个初值的选择，一个是将WLS 的结果选取为状态变量的预测初值，因为WLS属于无偏估计，可以满足EKF 的假设条件；另一个为初始滤波误差协方差矩阵的选取，因为EKF 并不完全依赖于初始时刻的滤波误差协方差矩阵P1的选取，所以一般取P1为单位阵即可。

3 FDIA检测原理

正常情况下，由于误差仅为系统中的噪声，所以WLS 和EKF 的结果是极为接近的，但当攻击发生时，被恶意更改的量测数据会使WLS 的状态估计更改为攻击者的预期量测数据；另一方面，由于转移矩阵（Fk-1）和系统误差（ωk）的约束效应，从EKF 获得的估计值只会小部分偏移，所以若两估计器结果相差过大，认为电网遭受了FDIA，检测公式为：

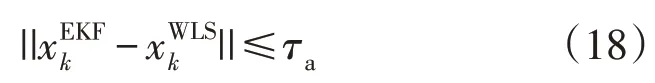
本文提出的虚假数据检测算法如图1 所示。

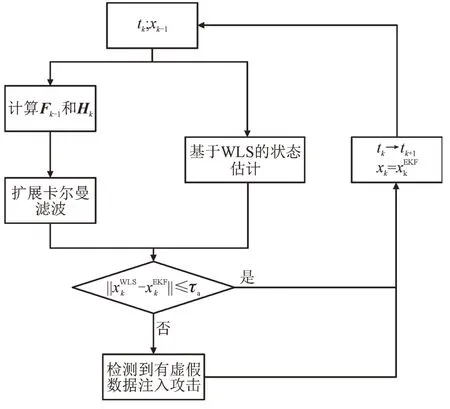
图1 虚假数据检测算法流程图Fig.1 Flow chart of detection algorithm for false data

4 算例分析

为了验证本文所提的虚假数据注入攻击检测算法的有效性，以改进的IEEE14 节点系统为例进行仿真，仿真的测试环境为MATLAB R2016b，硬件配置为Inter（R）Core（TM）i5-1135G7@2.40 GHz，内存容量为16 GB。

图2 显示了改进后的IEEE14 节点的接线图，与原系统相比，删除了节点3 和6 的发电机，并在节点5，11，13 处增添了发电机。为了体现电力系统的实时变化，将发电机节点分为风力（W），光伏（S），水力（H），火力（F）4 种类型，将负荷节点分为LC1，LC2，LC3 和LC4 四种类型，各类型节点的出力和负荷曲线详见图3 和图4。

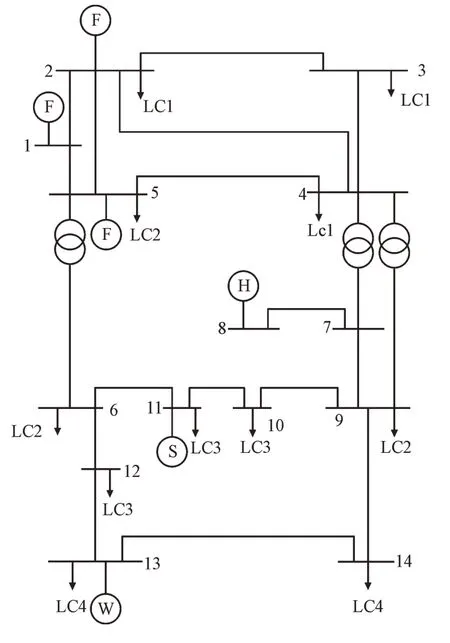
图2 改进后的IEEE14节点系统接线图Fig.2 Wiring diagram of improved IEEE 14-bus system

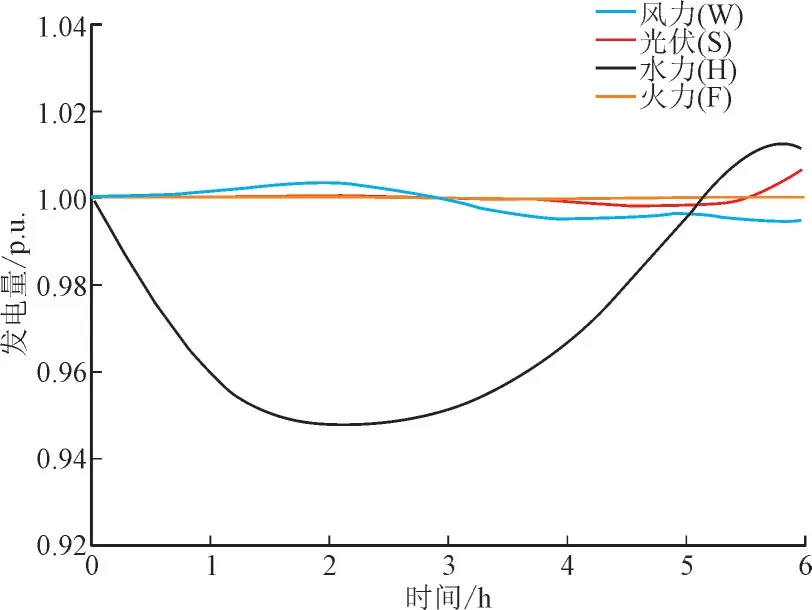
图3 发电机的出力曲线Fig.3 Output curves of generators

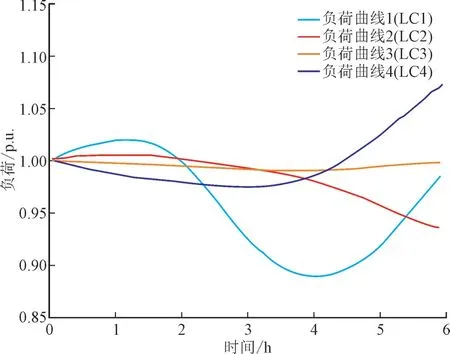
图4 负荷曲线Fig.4 Load curves

该系统各节点的功率如表1 所示，并将该系统设置为较高的冗余度。文献[26]提出了一种通过篡改局部子网的数据来构建攻击向量的方法，并使攻击向量具有隐蔽性与稀疏性，因此本文采用文献[26]中的虚假数据注入攻击模型来验证检测方法的有效性。

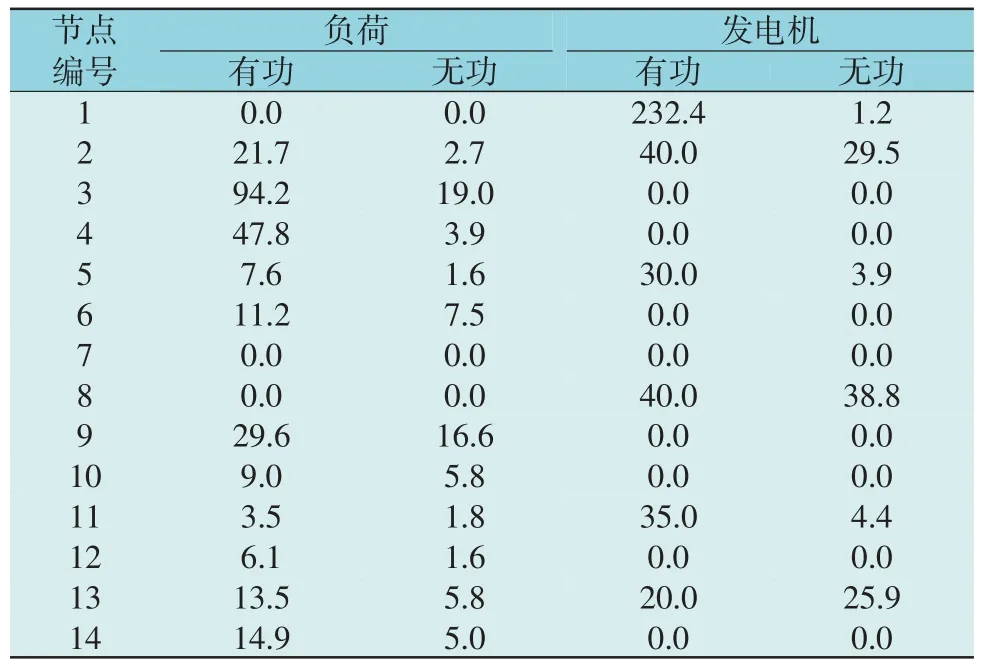
表1 系统节点的注入有功、无功功率Table 1 Active and reactive power injecting into system buses MW

图5 和图6 展示了在6 h 时段内没有攻击的情况下，节点7 处电压幅值和相角的残差，根据能量管理系统平均的采样周期，每30 s 进行1 次估计[24]，从图5 和图6 中很容易看出正常情况下，由噪声所造成的电压幅值、相角残差没有超过设定的阈值，因此未检测到FDIA。

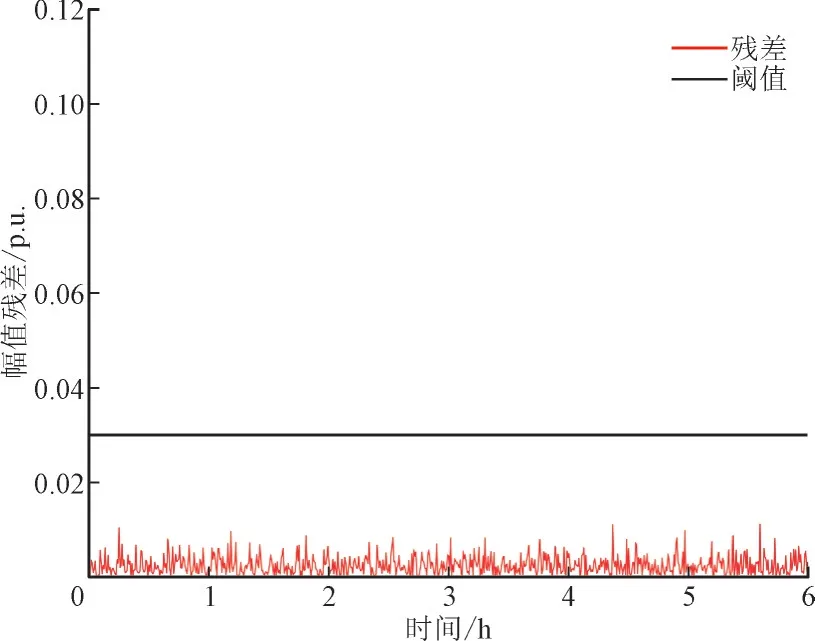
图5 正常运行节点7电压幅值残差Fig.5 Residual of voltage amplitude at node 7 in normal operation

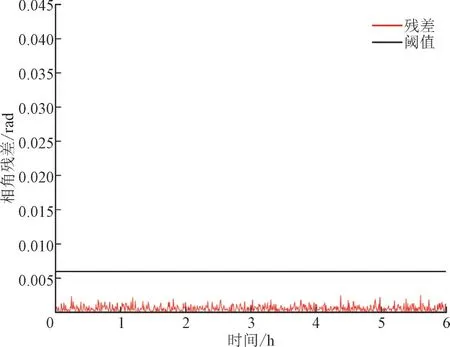
图6 正常运行节点7电压相角残差Fig.6 Residual of voltage phase angle at node 7 in normal operation

在图7 和图8 中，经过3 h 正常运行后，该系统遭到了FDIA，攻击之后经WLS 估计的节点7 的电压幅值达到1.18 p.u.，相角约变化了0.03 rad，1.18UN属于过电压，且BDD 并未显示存在异常数据，但实际的电压却是1.07，故可能会导致系统进行错误的调压行为。但EKF 是一种递归方法，下一时刻的值不仅受当前时刻量测量的影响，也会受上一时刻的估计状态的影响，故电压幅值和相角不会突变，而是随着时间的变化逐步趋于新的稳定，但这种变化是缓慢的，单利用EKF 无法做到实时检测FDIA，因此，可以利用两估计器的估计值残差来检测FDIA。

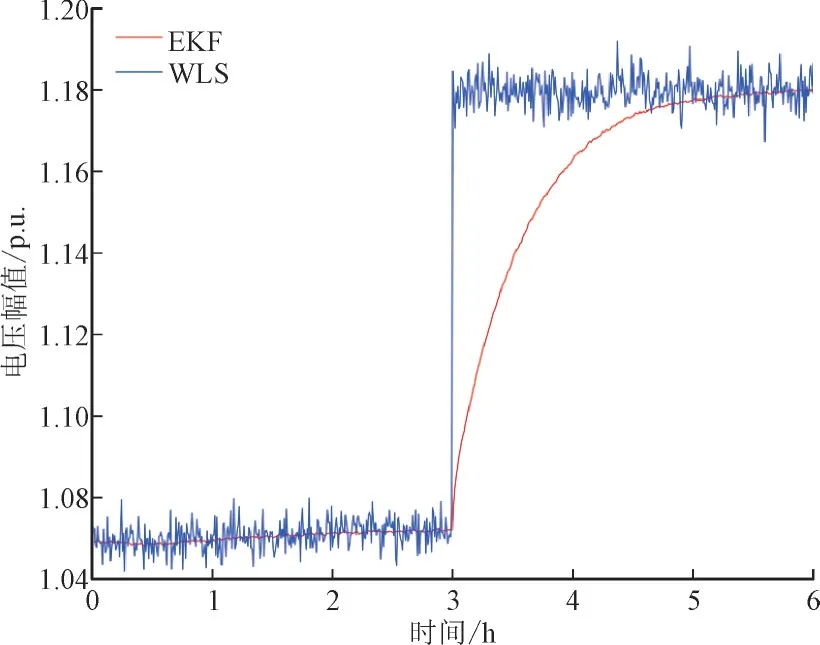
图7 遭受攻击时节点7的估计电压幅值Fig.7 Estimated voltage amplitude at node 7 under attack

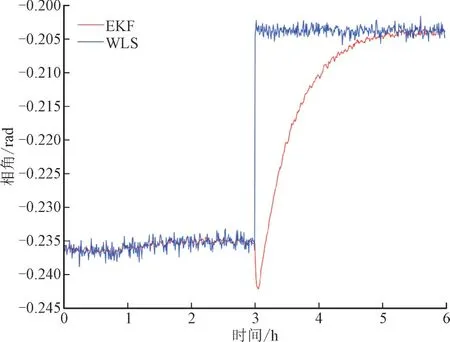
图8 遭受攻击时节点7的估计电压相角Fig.8 Estimated voltage phase angle at node 7 under attack

图9 和图10 给出了两估计器残差随时间的变化情况，在系统刚遭受攻击时，电压幅值和相角的残差达到最大，且在一个较长的时间段内，残差均大于所设定的阈值，所以该检测方法可以很好的打破FDIA 的隐蔽性。3δ原则也可保证在攻击之外的时间内不会误报。此外，一些负荷、发电机的突然变化以及计划外的系统事件，如设备停运等可能会导致WLS 与EKF 的估计值存在差异，这些事件也会产生误报。然而，这些事件很容易被电网所捕获，帮助调度员判断检测结果的正确性。

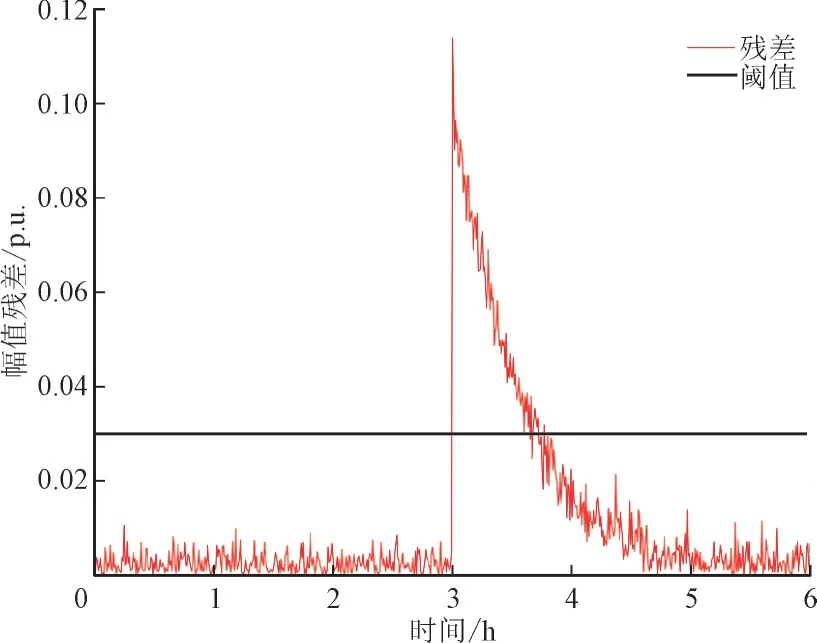
图9 遭受攻击后7节点处电压幅值残差Fig.9 Residual of voltage amplitude at node 7 after attack

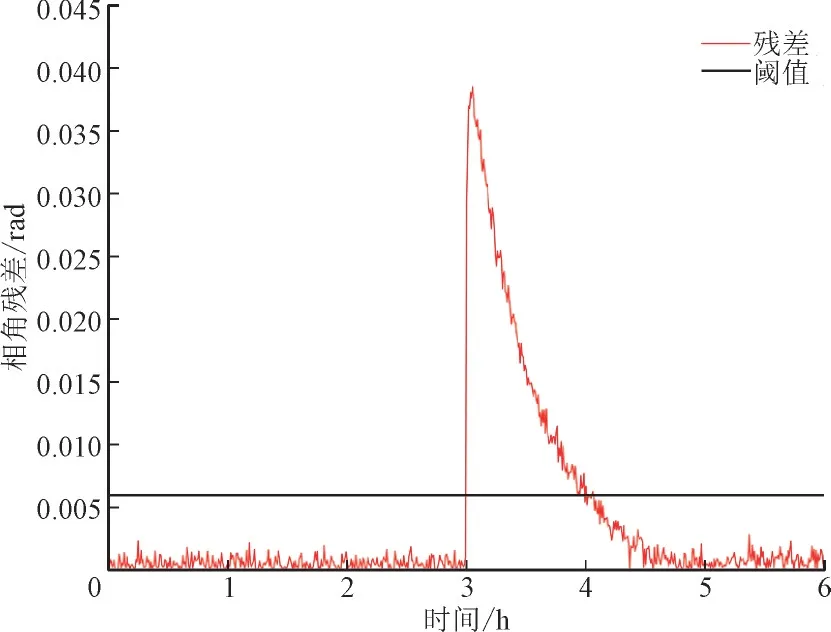
图10 遭受攻击后两估计器在7节点处电压相角残差Fig.10 Residual of voltage phase angle of two estimators at node 7 after attack

为了描述算法对FDIA 的检测性能，将检测到攻击至残差重新回到阈值以下的间隔时长定义为性能指标，该指标代表了该算法对FDIA 的反应能力。此外，将虚假数据注入增量与参考虚假数据注入增量的比值定义为攻击强度，来体现不同攻击程度FDIA 对检测性能的影响，仿真结果如图11所示。

从图11 可以看出，检测性能随攻击强度（无量纲）的增加而增加，这是因为EKF 可以抑制FDIA攻击强度的增加，而WLS 却是实时的，因此，偏差会增大，检测性能也会得到提高。通过和文献[27]的比较，可以看出，针对FDIA 的检测性能，本方法是要优于文献[27]的，这是由于文献[27]在求取状态转移矩阵的过程中使用的是Holt 两参数法，这种指数平滑法在对突变量进行处理的效果很差，因此在算法性能方面不如通过雅可比矩阵求逆的方式得到的时变状态转移矩阵，但本文算法对实时数据和负荷预测的需求要比文献[27]高。

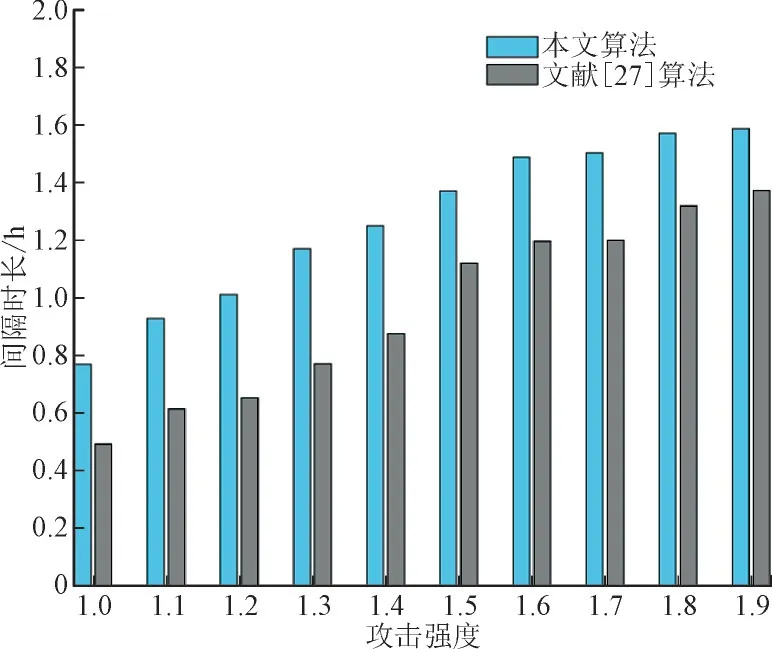
图11 不同攻击强度下不同算法检测性能对比Fig.11 Comparison of detection performance between different algorithms under different attack strength

5 结语

本文采用了将WLS 与EKF 结合的方法来实时检测FDIA，为了实现预测步中状态变量的变化，将潮流方程与发电机、负荷的功率曲线结合得到了时变的状态转移矩阵。在IEEE14 节点系统的算例分析结果表明所提方法能够有效检测FDIA，对于防范网络攻击具有一定的实际意义。本方法可以识别攻击，但不易找出具体的攻击向量，未来需要从剔除攻击向量这一方面开展更深入的研究。