基于FFT，DC-HC及LSTM的短期负荷预测方法

魏震波，余 雷

（四川大学电气信息学院，四川成都 610065）

0 引言

短期电力负荷预测是电力系统安排发电计划、经济调度电网、确定备用容量的基础，较高的预测精度对电网的安全可靠运行有着重要作用[1-3]。随着智能电表等监测设备的大量安装，基于大量数据分析进行短期负荷预测成为可能[4-5]。

多年来，为解决负荷预测中电力负荷序列因随机性、非平稳、非线性所带来的困扰，许多学者一直致力于探索更优的短期负荷预测方法[6-8]。有学者基于随机森林算法预测负荷[9]，有学者基于误差补偿预测负荷[10]，也有学者提出考虑利用负荷周期性特征即频率特性，先将电力负荷进行分类后再做预测，理论上可以提高总负荷预测精度。如文献[11-12]分别以变分模态分解和经验模态分解对总负荷进行信号分解，再对各信号分量进行负荷预测，有效提高了预测精度，但是模态分解模糊了单个样本概念，其运算过程亦可能造成样本特征的丢失。为保持样本独立性，可采用聚类算法对所有样本进行聚类[13]。

目前，主流聚类算法大致分为原型聚类、密度聚类、层次聚类3 类。其中，原型聚类是通过“原型”即样本空间中具有代表性的点进行聚类，Kmeans 算法是其典型代表，它假设同簇样本的分布空间为圆形，极大地限制了算法的合理分类，即使是更加优越的高斯混合聚类，依然假设同簇样本分布于椭圆空间中。并且，Kmeans 算法中初始簇心对最终结果会产生较大影响，亦无法识别噪音[14]，最终的聚类数目往往也需要人为选定[15]。密度聚类，其代表是DBSCAN 算法，它基于1 组邻域参数(ε,MinPts)来进行聚类，其中ε代表半径阈值，MinPts代表半径范围内需求的样本数。该算法虽然不需要手动设置聚类数，能自动识别噪音，其簇也不受样本分布形状影响[16]，但不同簇密度差异较大时性能受较大影响。此外，由于涉及2 个超参数，当数据规模较大时，调参会变得较为困难[17]。层次聚类的代表是自底向上的AGNES 算法，它不像原型聚类依赖于“原型”，不需要调参，但需要人为设定聚类数，无法识别噪音，而且聚类结果受簇间距离衡量方式影响较大[18]。因此，若将密度聚类与层次聚类算法相结合，则密度层次聚类算法（Density-based Clustering-Hierarchical Clustering，DC-HC）可自适应聚类数、甄别噪音、同簇样本不受样本分布形状限制，并且具备较高自适应度，多数情况下不需要手动调参。

综上成果与问题，本文考虑采用快速傅里叶变换（Fast Fourier Transformation，FFT）计算得到样本期望频率，并将其作为聚类特征量，采用DC-HC 算法进行聚类，实现对原始数据的预处理；然后，将处理后的各类样本按类叠加，分别使用长短时记忆（Long Short Term Memory，LSTM）神经网络进行负荷预测，将各分量预测结果再次叠加，得到最终负荷预测值。通过实际算例验证了本文思路及方法的合理性与有效性。

1 基于FFT的样本期望频率

1.1 样本频率模型

对有限长离散信号z(n),n=0,1,...,N-1，采用式（1）进行变换，即：

式中：Z（k）为z(n)的离散傅里叶变换，k=0,1,...,N-1；W为单位向量。

FFT 将z（n）按照n的奇偶性分解为偶数序列z1（n1）与奇数序列z2（n2），其长度都是N/2，即：

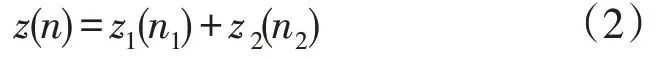
式中：n1为偶数，n2为奇数，且n1,n2⊆n。

则有：

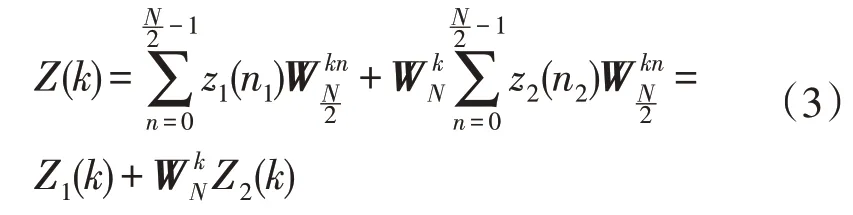
式中：Z1（k）和Z2（k）分别为z1(n1)和z2(n2)的离散傅里叶变换。

1.2 样本期望频率

总负荷由所有样本按时序叠加得到，对任一样本，由采样定理可知FFT 能求出最大频率为采样频率一半的振幅频谱，记某样本的s个对应频率值为w1，w2，…，ws，振幅为A1，A2，…，As，取σ1=1,2,...,s，σ2=1,2,...,s，提出单个样本的期望频率w计算方法为：

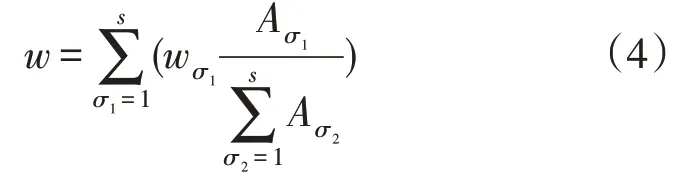
2 DC-HC算法

2.1 算法原理

首先计算出距离矩阵D，其第i行第j列元素di，j代表第i个样本与第j个样本的欧式距离。若数据集共有m个样本，则距离矩阵D为m×m的方阵，其后所有运算均围绕D展开。

簇与簇的合并遵循以下3 个原则：

1）除开自由点，所有簇都能通过内部距离运算确定请求与某外部点合簇或是拒绝与该点合簇。

2）规定小于等于5 个点的簇不能拒绝来自外部的合簇请求。

3）大于5 个点的簇可以拒绝来自外部的合簇请求。

以S表示样本点，C表示簇。对非自由点Si，其所在簇记为Cp。要考察簇Cp是否请求与其簇外点Sj合并，则需计算阈值T，若di，j≤T，则簇Cp请求与Sj所在簇Cq合并，反之则拒绝，阈值计算方法分为以下两种情况，分别用T1和T2表示：

（1）若Si所在簇Cp为初始簇，记Sl为与Si同簇的另一样本，则：

式中：y为对数几率函数，如式（6）所示：

式中：x为现有簇数与初始簇数的比值，x∈(0,1]。

（2）若Si所在簇Cp样本数目大于2，则通过D矩阵找到簇Cp内与样本Si距离不大于di，j的所有样本，加上样本Si本身，构成判定团体Gi。进一步在此定义“核心距离”：若判定团体Gi内共有a个样本，由于每2 个样本间有1 个距离，则共有a（a-1）/2 个距离值，找到其中a-1 个距离值使a个样本在拓扑结构上能够完全相连，并保证a-1 个距离值总和最小，则a-1 个距离值叫做判定团体Gi的核心距离，记为d1，d2，…da-1；判定团体的核心距离可以通过最小生成树算法求得[19]。进一步有：

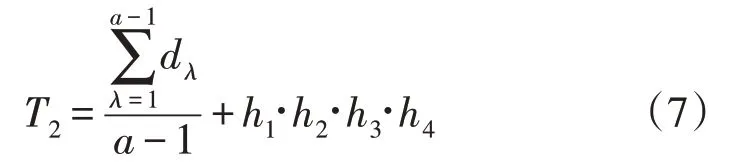
式中：λ=1,2,...,a-1；dλ为样本距离；h1，h2，h3，h4为修正系数，使所有数值处于一个合适区间。

希望T2的判定计算随簇数量的减少越来越严格，并且其减少速率的变化率也越来越大，即T2相对簇数的一阶导数为正，二阶导数为负，并且希望在簇数最多和最少两种极端情况下T2差别不应过大，这部分运算由系数h2完成，即：

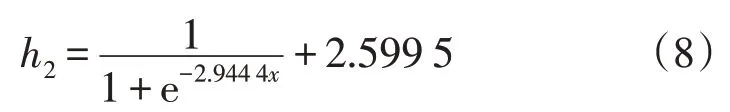
其中，h2原型函数为式（6）所表示的对数几率函数，式（9）、式（10）分别为其一阶导数y′和二阶导数y″，即:

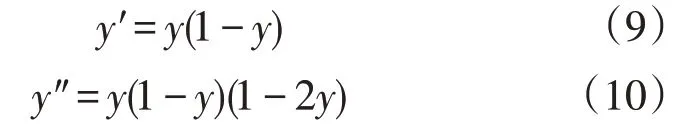
观察式（6）、式（9）、式（10）可知，对数几率函数基本满足系数h2控制需求，进一步对对数几率函数分别沿自变量和因变量方向进行图像的缩放和平移，设：

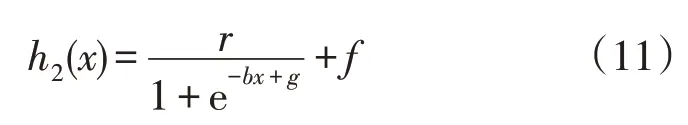
式中：g，b，r，f为控制图像变换的变量。

由式（9）、式（10）可知，对数几率函数本身就满足系数h2对一阶导数和二阶导数的需求，则图像不需要左右平移，即g=0，并且由于图像未进行左右平移，b，r，f的值并不影响系数h2对其低阶导数的需求；对于类似式（6）的函数，一般认为当函数值到达最大值的90%后增长率变缓，为保证系数变化具有差异性并考虑自变量范围x∈(0,1]，则有：

求解式（12）得b=ln19≈2.944 4；为避免簇数最多和最少两种极端情况下系数差异过大，考虑如式（13）的约束：

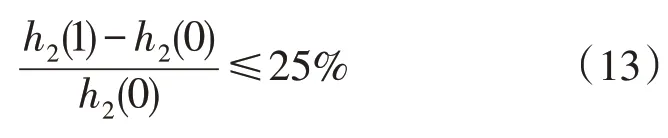
求解式（13）得0.263 2f-0.684 2r≥0，取r=1，则可取f=2.599 5。

系数h3与小团体Gi中样本个数a成负相关，即a越大，样本Sj与小团体Gi相对而言越远，T2越小。h3计算如式（14）：

参考以标准差判定离群点的方式，取ζ=1,2,...,a-1，则系数h4为Gi的核心距离标准差为：

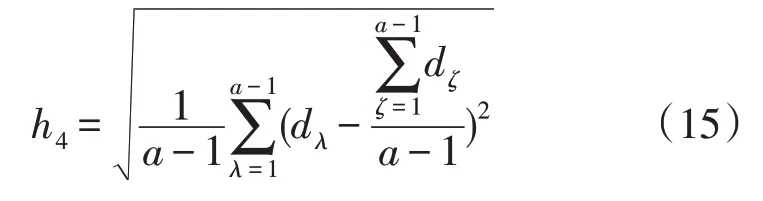
式中：dζ为样本距离。

若满足条件di，j≤t，则簇Cp请求与簇Cq合并，受约束于2.1 节合簇原则，对称性地计算簇Cq（Sj）与点Si之间的阈值，并进一步判定簇Cq是否请求与簇Cp合并。

2.2 算法流程

DC-HC 算法流程如下：

1）根据输入样本计算得到距离矩阵D。

2）由D矩阵找到所有互为彼此最近样本的2个样本构成初始簇，并在D矩阵中将所有簇内距离值位置置为非数值。

3）找到D矩阵中的当前最小数值di，j，依照2.1节方法计算阈值并判定是否合簇，并将di，j和dj，i位置置为非数值。若不合簇则跳到步骤5）。

4）将新合簇形成的簇内距离值在D矩阵中置为非数值。

5）若D矩阵不全为非数值，则返回步骤3）。

2.3 算法效果测试

选取费舍尔鸢尾花数据集（iris）、Matlab 内置聚类测试数据集（kmeansdata）、三角圆数据集（data1）、双月数据集（data2）4 个标准数据集，分别采用Kmeans，AGNES，DBSCAN，DC-HC 4 种聚类方法对4 个数据集进行聚类。

层次聚类算法AGNES 选用豪斯多夫距离衡量Cp和Cq2 簇间距离distH（Cp，Cq）[14]，即:

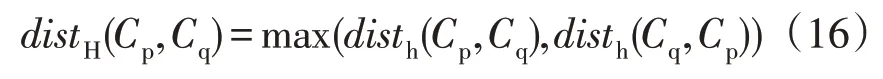
其中，

式中：disth(Cp,Cq)为从Cp到Cq的单方向豪斯多夫距离。

使用4 组数据集和4 种聚类方法，可得到16组聚类结果，分别采用以下6 种聚类内部评估指标进行测评：（1）DB 指数[14]；（2）Dunn 指数[14]；（3）轮廓指数[14]；（4）CH 指数[20]；（5）VCV 指数[21]；（6）MST 指数[21]。

数据集data1 和data2 在4 种聚类算法下的分类情况如图1 所示。其中，横、纵坐标代表相对位置，无单位，下文同。

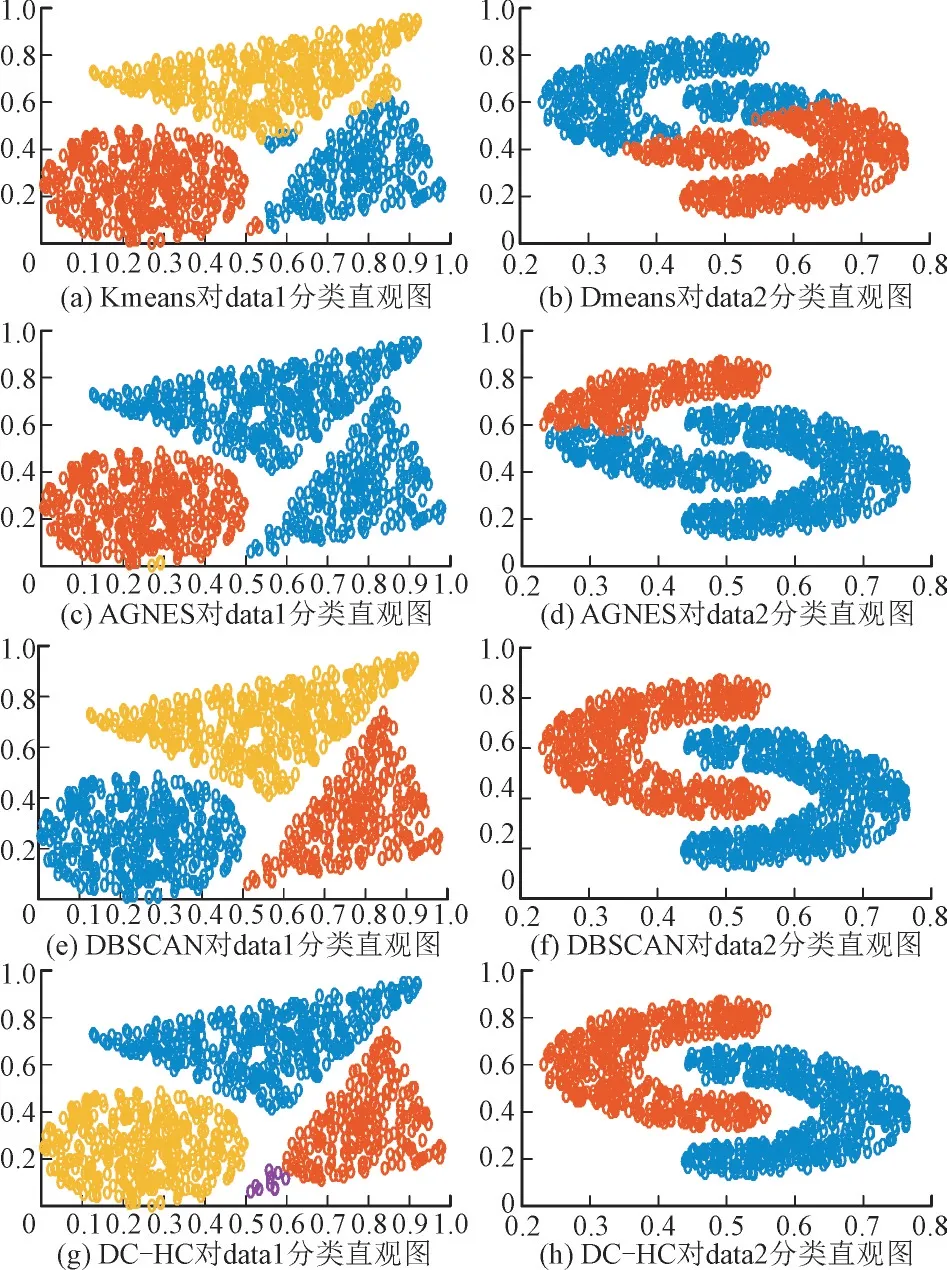
图1 4种聚类算法对data1和data2的分类直观图Fig.1 Visual distribution maps of data1 and data2 clustered by fourclustering algorithms

以图1（e），（f）的分类结果作为外部评估标准数据，对4 种聚类算法的聚类效果分别采用3 种聚类外部评估指标进行测评：（1）Jaccard 系数[14]；（2）FM指数[14]；（3）Rand 指数[14]。

参照各指标在不同数据集下的不同聚类算法最优得票进行统计。若不同算法对同一数据集有相同分类方案且在某评估指数下最优，则均得票，统计结果如表1 所示。

表1 各聚类算法最优得票统计Table1 Optimal voting statistics of clustering algorithms

综合考虑表1 结果和各算法特性可知：（1）就经验预期而言，AGNES 算法与Kmeans 算法表现相近，但对比图1（a）和（c）评估结果，AGNES 算法在数据集data1 下的表现远不如Kmeans 算法。若排除data1，采用AGNES，Kmeans 两种算法对剩余3个数据集应用9 个指标进行最优得票数统计，并经计算可知Kmeans 算法得11 票，AGNES 算法得10票，与预期相符，说明豪斯多夫距离不适用于数据集data1，进一步说明簇间距离衡量方式将会对类似AGNES 的层次聚类算法产生决定性影响；（2）DCHC 算法由于继承了密度聚类不受样本分布形状的特性，因此其在data1 和data2 两个特定数据集下表现略劣于DBSCAN 算法，但远优于另外2 种算法。由此可以预见，当数据呈现高维特性时，样本点在超空间中的分布形状会更加趋向于非圆形化，这时DC-HC 算法和DBSCAN 算法将更具优越性。在最终得票统计上，DBSCAN 算法略优于DC-HC 算法，但DBSCAN 算法存在二维超参数，当数据量较大时调参困难；并且DBSCAN 算法无法应对不同簇密度差异较大的聚类场景，而密度差异往往在高维数据下被扩大。因此面对大量高维数据时，DC-HC 算法适用性更强。

使用data1 和data2 两个可视数据集随机添加15 个样本点对DC-HC 算法进行抗噪性测试，噪音点均用黑点表示，测试结果如图2 所示。

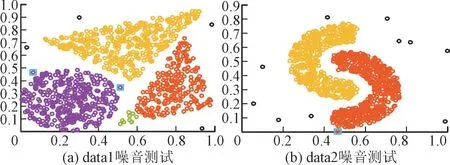
图2 DC-HC算法抗噪性测试Fig.2 Noise resistance testing of DC-HC algorithm

对比图2 与图1（e），（f）可知，蓝色方框选中的点为新添加的样本点，但DC-HC 算法并未将其判定为噪音点，而距离更远的点才被判定为噪音，可见DC-HC 算法具备良好的抗噪能力。

3 LSTM网络

循环神经网络（Recurrent Neural Network，RNN）被广泛用于各类时序问题，然而在误差沿时间反向传播的过程中，梯度进行多次叠加将会导致梯度消失或梯度爆炸，因此RNN 很难处理长时序问题。进而产生一种改进的循环网络：LSTM 网络[22-24]。

为解决梯度难以沿时间长距离反向传播的问题，LSTM 新增单元状态c并引入“门”的概念。其输入包括μ，β，c3 类，输出包括β，c2 类。其中μt为t时刻输入，βt为t时刻网络输出，如图3 所示。

图3 LSTM时序逻辑结构Fig.3 Structure of LSTM sequential logic

4 算例分析

4.1 数据选取

本文以爱尔兰可持续能源管理局（Sustainable Energy Authority of Ireland，SEAI）于2011 年5 月发布的爱尔兰智能电表实测用户用电数据作为实验数据集[25]。

4.2 数据预处理

采用FFT 计算每个样本的振幅频谱，根据式（4）计算对应期望频率；再以期望频率作为特征量使用DC-HC 算法对爱尔兰电力负荷数据集进行聚类，共有10 个样本被DC-HC 算法归类为噪音。

4.3 负荷预测

4.3.1 LSTM负荷预测

将各类负荷（噪音样本算作噪音类负荷）按类叠加，以1 h 负荷量为1 个时间节点，选取1 到120时间节点划分为训练集，121 到144 时间节点作为测试集，使用LSTM 神经网络进行负荷预测，预测结果如图4 和图5 所示。由图4 可知，6 类实际负荷中的大部分负荷曲线与预测曲线具有较高的一致性，预测效果较好。噪音类负荷曲线规律性较弱，所以预测效果并不理想，但由于噪音类样本较少，噪音类总负荷量相对于相同时间内负荷总量很少，因此噪音类负荷预测对最终的总负荷预测影响很小。

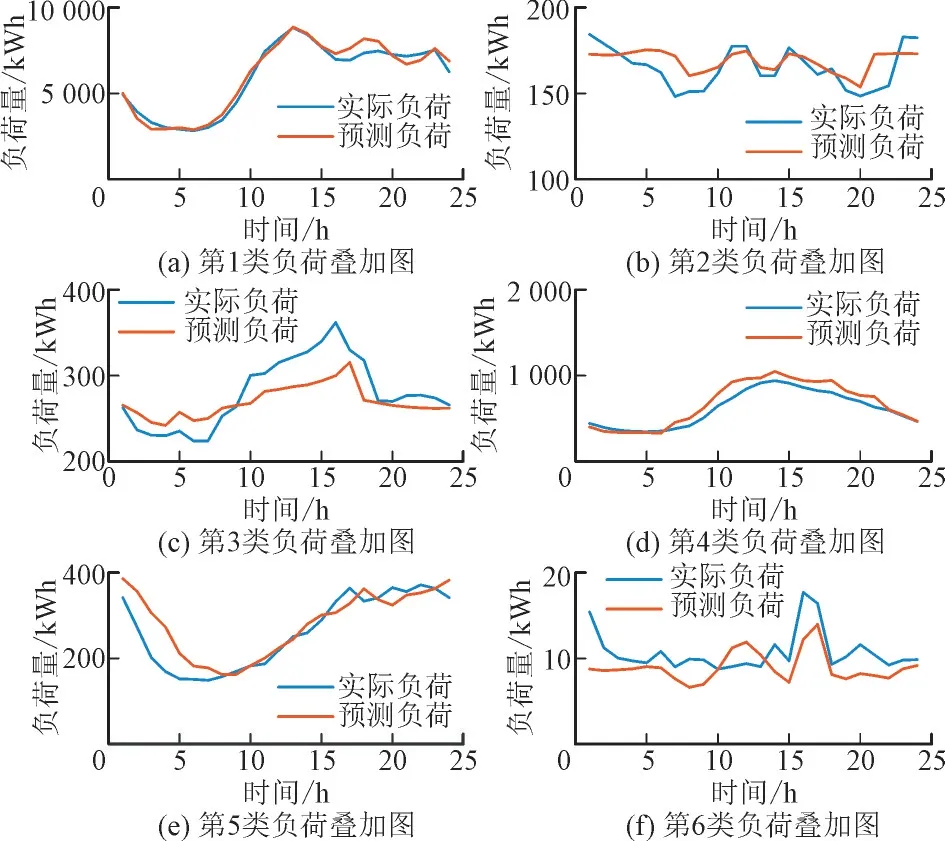
图4 6类负荷实际曲线及预测曲线Fig.4 Actual and predictive curves of six kinds of loads

图5 噪音类负荷实际曲线及预测曲线Fig.5 Actual and predictive curves of noise loads

使用本文所提FFT-DC-HC-LSTM 算法，将121—144 共24 个节点所有预测结果进行叠加后，得到图6 曲线。

图6 24个节点总负荷曲线及预测曲线Fig.6 Total load and forecating load of 24 nodes

由图6 可知，采用本文算法进行负荷预测的结果与实际负荷的运行规律基本一致。

4.3.2 聚类算法对LSTM负荷预测影响

为评估各方案预测精度，进一步采用均方根误差（Root Mean Square Error，RMSE）和平均绝对百分误差（Mean Absolute Percentage Error，MAPE）评估预测效果，数学表达为：

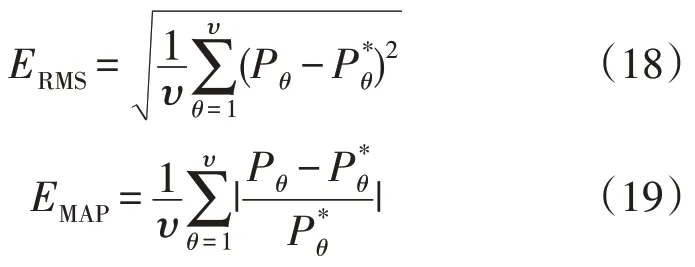
式中：为第θ个时段的实际负荷值；Pθ为第θ个时段的预测负荷值；υ为预测时间内的节点数。

将4.3.1 节预测方案与以下4 种方案进行对比：（1）使用Kmeans 聚类负荷数据后进行预测；（2）使用AGNES 聚类负荷数据后进行预测；（3）使用DBSCAN 聚类负荷数据后进行预测；（4）不使用聚类方法预处理负荷数据，直接进行负荷预测。对比结果如表2 所示。

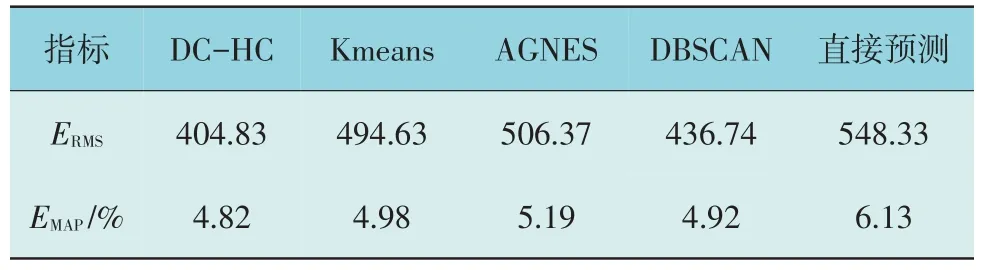
表2 预测方案误差值对比Table 2 Comparison of error values between predictive schemes

由表2 数据可知：（1）对原始电力负荷数据使用聚类算法进行预处理后再按类分别进行负荷预测，可有效降低预测总误差；（2）在以负荷预测为目的负荷数据聚类预处理过程中，DC-HC 算法表现优于其它算法。

4.3.3 不同预测算法比较

在均使用DC-HC 算法进行数据预处理的前提下，采用LSTM、门控循环单元（Gated Recurrent Unit，GRU）、非线性自回 归（Nonlinear Autoregressive，NAR）、RNN、多层感知机（Multilayer Perceptron，MLP）、支持向量回归（Support Vector Regression，SVR）及一种集成决策树（AdaBoost-Decision Tree，AB-DT）作为预测算法进行预测误差及稳定性对比，对比结果如表3 所示：（1）预测误差，每个预测算法均独立训练20 批次并取多次预测的平均值作为最终结果进行误差计算；（2）稳定性，单个预测算法每批次训练的最终预测结果均计算误差，并以此计算所有误差值的标准差。

由表3 数据可知：（1）MLP，SVR 和AB-DT 算法虽然输出稳定，但由于并非时序模型，因此在预测精度上并不理想；（2）综合预测精度和算法稳定性，在负荷预测问题中，LSTM 算法应被优先考虑使用。

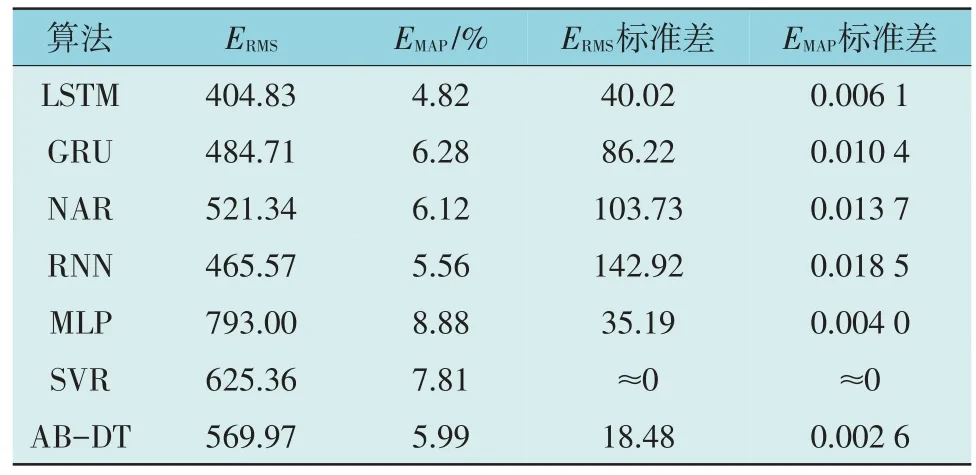
表3 不同预测算法比较Table 3 Comparison of different predictive algorithms

5 结论

本文提出了一种基于FFT、DC-HC 和LSTM 网络的短期负荷预测方案，借助FFT 得到负荷数据期望频率并以之作为特征量，使用DC-HC 算法聚类负荷，再将聚类结果按类分别使用LSTM 进行负荷预测，最终叠加各分量得到预测总负荷。研究结论具体如下：

1）通过FFT 进行特征提取再聚类电力负荷数据的按类预测方法，可有效提高短期负荷预测精度。

2）相较其它算法，LSTM 算法应用于本文负荷数据进行预测具有更高精度且更加稳定。

3）相较其它聚类算法，DC-HC 算法在负荷预测中具有更好的数据预处理效果。

4）DC-HC 算法具有自适应聚类数、抗噪性、簇空间分布自由等优点，相较传统聚类方法具有更大的适用范围和更强的适用性。

接下来，研究受外部相关时序变量影响的时序数据预测模型是今后工作重点。