一种融合电气量和开关量的电网Petri网故障诊断方法

肖 丰，张彼德，孙文成，王 涛

(1.西华大学电气与电子信息学院，四川 成都 611730；2.国家电网公司西南分部，四川 成都 610041)

随着电力系统建设的不断完善，电网结构变的日趋复杂，电网故障对电力系统带来的影响也越来越大，因此研究电网故障诊断方法对电力系统的安全可靠运行具有重要意义。目前，学者们已提出了各种电网故障诊断方法[1-6]，并在电网故障诊断应用中取得了一定成效，但也存在些许不足。

Petri网是对离散事件和动态系统建模分析的理想工具。故障元件、继电保护和相应断路器动作的逻辑关系可通过图形进行简单的描述，且矩阵形式的推理也具有直观且逻辑清晰缜密的优点，将Petri网应用于电网故障诊断具有较好的应用前景。但现有的方法中，大部分仅对开关量分析，故障信息源单一，诊断结果严重依赖开关量的正确性。而电气量在准确性、容错性和完备性等方面都有着无法比拟的优势，对电气量进行分析能有效地提高故障诊断的准确性。

因此，本文提出了一种计及电气量和开关量的电网Petri网故障诊断方法，从电气量和开关量出发，同时考虑了开关量的时序关联特性。首先，根据开关量确定停电区域，针对电气量利用希尔伯特黄变换和模糊逻辑分析，使连续的电流波形离散化，通过模糊逻辑Petri网计算得到2个故障概率表征；其次，对开关量时序信息进行约束检查，剔除错误故障信息，并采用高斯函数以确定时序模糊Petri网的初始置信度，建立元件的通用Petri网模型，通过模糊推理机制计算得到一个故障概率表征；最后，采用D-S证据理论对3个故障概率表征进行信息融合，得到元件最终的故障概率。通过新英格兰10机39节点系统的多组故障案例测试表明，在保护和断路器拒动/误动、信息丢失和时标出错等复杂故障情形下，均能准确诊断出故障元件，对其有效性进行了验证。

1 基于电气量的Petri网故障诊断

电气量故障诊断的分析对象是线路元件的电流波形。由于Petri网是对离散事件、动态系统的分析工具，无法直接对电流波形进行处理，因此需在Petri网推理分析的前端，添加故障特征提取模块和模糊逻辑分析模块，使得连续的电流波形离散化，以便后续的分析计算。

1.1 故障特征提取模块

对采集到的电流波形利用希尔伯特黄变换(hilbert-huang transfrom，HHT)[7]进行时频域分析，得到的Hilbert边际谱h(ω)和Hilbert边际能量谱S(ω)能清晰地反映出原信号的时频特性。在实际运行电网中，电网发生故障的时刻，线路电流立刻发生突变，故障元件出现比非故障元件更多的高频分量，非故障元件的低频分量更多，利用这一故障特征，定义第i个元件的频率畸变度为

Fi=P2/P1

(1)

式中P1为h(ω)中的低频(f<100 Hz)分量；P2为h(ω)中的高频(f>100 Hz)分量。

故障发生后，故障元件的电流信号总能量相比非故障元件会更高，因此定义第i个元件在故障时刻后2个周波内的故障能量度为

(2)

式中fs为采样频率，本文取10 kHz。

1.2 模糊逻辑分析模块

模糊逻辑分析是一种模拟人脑对不确定性概念的判断和推理的方法。通常借助隶属度函数来处理模糊关系，可将其表示为一个映射μ：x→[0,1]，μ为隶属度函数，x为元素的隶属度。

隶属度函数的选取可以是任意的，分段函数能清晰地表达故障诊断的逻辑关系，故在此采用图1所示的分段函数作为隶属度函数。在故障诊断中，常采用模糊语言“高”和“低”来描述电流变化程度。

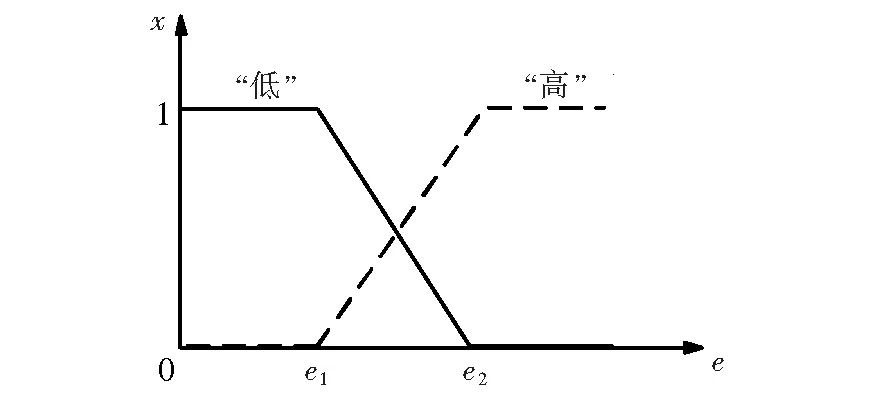
图1 隶属度函数Figure 1 Membership function

关于模糊语言“高”的隶属度函数，e∈[0,e1]，隶属度为0；e∈[e1,e2]，输入与输出成正比；e∈[e2,∞]，隶属度为1。关于模糊语言“低”的隶属度函数，e∈[0,e1]，隶属度为1；e∈[e1,e2]，输入与输出成反比；e∈[e2,∞]，隶属度为0。

首先分别对每个元件的电流波形进行HHT分析，进而得到该元件的频率畸变度Fi和故障能量度Ei；然后分别将每个元件的频率畸变度Fi作为模糊逻辑分析的输入值，通过分段函数计算得到2个关于模糊语言“高”和“低”的隶属度，其为一个概率值，并作为模糊逻辑Petri网的初始置信度。故障能量度Ei同理计算。

1.3 模糊逻辑Petri网故障识别框架

由特征提取模块、模糊逻辑分析模块和模糊逻辑Petri网构成基于模糊逻辑Petri网的故障识别框架。

在故障发生前后，故障元件比非故障元件出现了更多的高频分量，且电流信号总能量也更高。模糊逻辑Petri网实际上是对上述模糊逻辑的量化，将基于电气量的模糊逻辑Petri网(fuzzy logic petri net，FLPN)定义为一个七元组集合FLPN=(P,T,F,I,O,Th,M)。

1)P=(P1,P2,…,Pn)为库所集合，n为库所个数。

2)T=(T1,T2,…,Tm)为变迁集合，m为变迁个数。

3)F⊆P·T∪T×P，表示连接库所与变迁之间的有向弧。

4)I：P→T表示输入矩阵，I=[ωij]，[ωij]∈[0,1]，若pi为tj的输入，则ωij表示该有向弧的权值；若pi不是tj的输入，则ωij为0。其中，i=1,2,…,n；j=1,2,…,m，表征前提条件对结论的贡献程度。

5)O：T→P表示输出矩阵。

6)Th：Th→[0,1]表示变迁tj(tj∈T)对应的阈值λj，Th=(λ1,λ2,…,λm)。

7)M=(m1,m2,…,mn)表示库所对应的置信度，m∈[0,1]。

以3个元件为例，基于模糊逻辑Petri网的故障识别框架如图2所示。图2中，“H”表示模糊语言“高”，“L”表示模糊语言“低”。P1～P6表示初始库所，P7～P9表示终止库所，L1～L3为诊断出的故障元件，T1～T3表示变迁。第i个变迁对应第j条输入弧的权值均为1/3。

在文1.2节中，得到的模糊逻辑分析输出值，将其作为模糊逻辑Petri网的库所初始置信度，经过矩阵形式的模糊推理机制[8]的迭代计算，得到第i个元件的2个故障概率表征，即频率故障度(frequency distortion degree，FDD)和能量故障度(energy distortion degree，EDD)，再对其按式(3)、(4)进行归一化处理，作为证据体，等待下一步的信息融合。

(3)

(4)

2 基于开关量的Petri网故障诊断

开关量故障诊断的分析对象是继电保护、断路器动作信息，将基于开关量的时序模糊Petri网(temporal fuzzy petri net, TFPN)定义为一个十元组集合TFPN=(P,T,F,I,O,Th,t,tR,Δt,M)。

1)t=(t1,t2,…,tn)为库所的延时约束矩阵，表示保护的整定延时、断路器的动作延时。

2)tR=(tr1,tr2,…,trn)为库所实际录得时间。

3)Δt=(Δt1,Δt2,…,Δtn)为库所的延时约束不确定矩阵，表示时间距离的不确定度。

4)其余元素同文1.3节。

2.1 图形化建模

电网结构可通过对元件配置各级保护和断路器的不同来体现，而传统的Petri网模型对电网结构的改变不具备适应性，因此基于开关量的时序模糊Petri网对每个元件建立通用模型，避免了电网拓扑结构改变时对模型及相关矩阵的修改。通用模型考虑了输电线路配置的主保护、近后备保护和远后备保护。当电网结构发生变化时，按修正部分保护及断路器的动作概率，分别为

(5)

(6)

式(5)、(6)中m1、n1分别为保护、断路器动作数；M1、N1分别为该元件配置的保护数和该保护相关的断路器数；i1、i2分别为修正前的保护、断路器动作概率。

基于开关量的时序模糊Petri网的通用模型如图3所示，第1层中，各个库所为各级保护和相应断路器；第2层(P1～P6)是中间库所，无实际物理意义；第3层(P7～P15)是过渡库所，表示在输电线路的继电保护中，各级保护和断路器的相互配合关系；最后一层表示元件。

图3 基于开关量的时序模糊Petri网通用模型Figure 3 General model of temporal fuzzy Petri net based on the remote communication

2.2 时序特性与时序约束

根据继电保护原理，故障发生、各级保护装置和相应断路器动作存在固有动作时间，三者产生的警报信息时刻分布在一定范围之内，并在时间上相互配合、相互约束。时序约束关系包括一元时间点约束和二元时间距离约束。

1)一元时间点约束。定义事件确切发生的时间点为t，鉴于系统实际运行的诸多不确定因素，需用t和不确定度Δt来共同定义，即事件发生时刻的时间区间T(t)为[t-Δt,t+Δt]。

2)二元时间距离约束。定义事件i时间点ti和事件j时间点tj之间的确切长度为时间距离dij，即dij=ti-tj。时间长度的不确定度用Δd表示，则时间点ti和tj之间的时间距离为D(ti,ti)=[dij-Δd,dij+Δd]。

若事件a能触发事件b，称事件a是事件b的原因事件，事件b是事件a的结果事件。将一元时间点和二元时间距离的正反向时序推理运算作如下定义。

正向时序推理是已知原因事件a的时间点约束和事件a、结果事件b之间的时间距离约束，正向推理得到事件b及其相应的时间点约束，事件b的时间点约束为

T(tb)=T(ta)+D(ta,tb)=[ta+dab-

(7)

同理，反向时序推理是已知结果事件b的时间点约束和事件b、原因事件a之间时间距离约束，反向推理得到事件a及其相应的时间点约束，事件a的时间点约束为

T(ta)=T(tb)-D(ta,tb)=[tb-dab-

(8)

因此，针对每个可疑故障元件相应的开关量进行时序推理分析。通过判断时序信息是否满足时序约束条件，来甄别错误警报信息，可有效地提高诊断的容错性。时序信息约束检查步骤如下：

第1步：确定停电区域，停电区域内的元件均视为可疑故障元件；

第2步：针对每一个元件，划分与该元件相关的开关量，形成不同集合；

第3步：对每个集合分别进行时序推理分析，利用获得的开关量动作时刻进行反向时序推理，得到故障发生的一元时间点约束；

第4步：合并每个集合故障发生的一元时间点约束，得到故障发生的一元时间点总约束；

第5步：对故障发生的一元时间点总约束进行正向时序推理，得到各个库所的一元时间点约束，再与获得的时序信息相比较，便可甄别不满足时序信息的错误开关量信息。

由继电保护的配置原理，定义故障发生时刻到主保护、近后备保护和远后备保护动作时刻的时间距离约束为[9]d[tr,tm]∈[drm-Δdrm,drm+Δdrm]=[10,40]，d[tr,tp]∈[drp-Δdrp,drp+Δdrp]=[260, 340]，d[tr,ts]∈[drs-Δdrs,drs+Δdrs]=[950, 1070]，ms。下标r为故障发生，下标m为主保护，下标p为近后备保护，下标s为远后备保护。另外，定义各级保护与相对应断路器动作的延时区间为d[tR,tb]∈[dRb-ΔdRb,dRb+ΔdRb]=[20, 40]，下标R表示触发断路器的各级保护，下标b表示各级保护相应的断路器。

2.3 模型参数的设定

1)库所初始置信度。首先利用时序约束关系，对开关量进行时序约束检查，剔除不满足时序约束关系的错误信息后，再通过高斯函数运算、时序信息关联特性的挖掘分析，为库所的初始置信度重新赋值，代替人为经验取值，能提高诊断模型的容错性，并有效增大保护、断路器动作的真实性，从而提高故障诊断的准确性。对初始置信度的赋值，即

α(tr)=k·exp(-(tr-t)2/(2Δt)2)

(9)

事件期望发生的时间区间为[t-Δt，t+Δt]，t为期望的事件发生时间点，Δt为其不确定度，tr为电力系统实际采集的事件发生时间点，k为可靠性系数，则取值为0.9。

改进的赋值方法满足电力系统发生故障后时序推理的逻辑关系，若tr在[t-Δt，t+Δt]区间内，说明采集的时间点在期望的时间范围中，可有较高的概率值输出，则获得的初始置信度值更大；若tr不在[t-Δt，t+Δt]区间内，说明事件没有发生在期望的时间区间内，获得的初始置信度值较小。tr离时间距离越远，α(tr)就越小。若电力系统未录得该事件的实际发生时间，则认为事件发生时间为tr=∞，α(tr)趋于0。而对于未收到警报信息的事件，由于警报信息存在不确定性，均赋予事件较低的概率值0.2作为初始置信度。

2)变迁的输入弧和输出弧参数。故障发生后，由保护、断路器动作切除故障，恢复供电。认为保护动作和断路器跳闸对规则的重要性一致，设置保护库所和断路器库所到变迁的输入弧权值均为0.5。由于线路配置的各级保护相互配合对规则的影响不同，因此采用不同的权值组合，以提高故障诊断的容错性，如图3所示，其余输入弧权值为1。

3)变迁可靠性。认为主保护动作、近后备保护动作和远后备保护动作的影响程度不同，依次按照重要度的不同，赋予变迁输出弧的置信度依次为1、0.95、0.85[10]，其他情况设置变迁输出弧的置信度均为1。此外，设置变迁的阈值均为0.2。由矩阵形式的模糊推理机制计算得到第i个元件故障概率表征，即模糊故障度(fuzzy fault degree, FFD)，再对其进行归一化处理形成证据体。

3 诊断流程

故障诊断流程如图4所示，具体步骤如下。

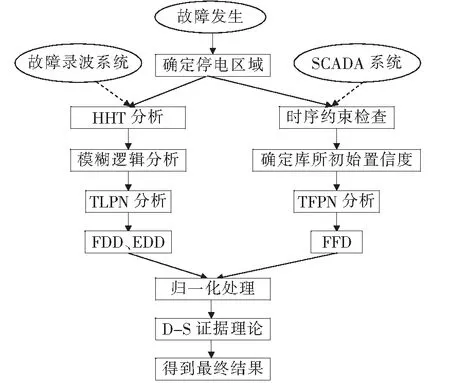
图4 故障诊断流程Figure 4 Process of fault diagnosis

1)故障发生，获取开关量，确定停电区域，形成可疑故障元件集。

2)针对可疑元件提取元件的电流波形数据。

3)电流波形HHT分析后提取故障特征量，由模糊逻辑分析确定模糊逻辑Petri网的初始置信度，矩阵形式的迭代计算后，得到频率故障度和能量故障度。

4)对开关量时序信息进行约束检查，剔除不满足时序约束的错误信息。

5)分析挖掘开关量时序信息，确定库所初始置信度，经矩阵形式的迭代计算后，得到模糊故障度。

6)各故障度归一化处理后，形成待融合证据体，采用D-S证据理论[11]进行信息融合，得到元件最终的故障概率。

4 算例分析与对比

通过采用PSCAD/EMTDC软件搭建新英格兰10机39节点系统，如图5所示，并模拟故障场景来进行仿真，并采用MATLAB软件实现故障诊断程序，以验证该方法的有效性。设置仿真步长为100 μs，仿真时长为0.2 s，故障发生时刻为0.08 s，故障持续时间为0.07 s。故障发生后，由于事先未知故障类型，应先计算三相故障特征值，选取三相中故障特征值最大相作为该元件的故障特征值。认为故障概率大于0.7的元件为实际故障元件，但在实际应用中故障概率超过0.5的元件，调度人员仍应将该元件纳入需关注的范围[10]。

图5 新英格兰10机39节点系统结构Figure 5 New England 10 machine 39 bus system

下面用一个简单的故障案例场景来描述故障诊断具体过程。该故障案例场景为线路L4-14发生单相短路故障时，主保护L4-14Sm动作并跳开断路器CB(4)-14，主保护L4-14Rm动作但断路器CB(14)-4拒动，导致事故扩大，远后备保护L13-14Rs和L14-15Ss动作，由断路器CB(13)-14和CB(15)-14动作来切除故障。该故障场景模拟的是主保护对应的断路器拒动。为方便分析计算，时标取相对时间：(L4-14Sm，25)，(L4-14Rm，27)，(CB(4)-14，58)，(L13-14Rs，1 030)，(L14-15Ss，1 033)，(CB(13)-14，1 055)，(CB(15)-14，1 060)，ms。下标S表示线路左(或上)端，下标R表示线路右(或下)端。

1)搜索停电区域，确定可疑故障元件集Φ，Φ={L4-14, L13-14, L14-15}，并将开关量划分为每个元件对应的集合。

2)针对以上3个可疑故障元件，有针对性地提取和处理电流波形，无需历遍所有元件，可大大地提高故障诊断效率。以元件L4-14为例，元件L4-14的A相电流如图6所示。

图6 A相电流波形Figure 6 Phase A current waveform

3)对元件L4-14的A相电流进行HHT分析，得到Hilbret边际谱和Hilbret边际能量谱，计算出频率畸变度为0.042 2，故障能量度为0.715 2。通过仿真采集了正常状态和不同故障类型的电流数据共35组以确定隶属度函数(见图1)中e1和e2的取值。在计算频率畸变度的隶属度时，e1取值为0.005，e2取值为0.05；在计算故障能量度的隶属度时，e1取值为0.001，e2取值为1.5。通过模糊逻辑分析确定模糊逻辑Petri网模型的初始置信度，经过矩阵化推理得到频率故障度和能量故障度，频率故障度为0.478 9，能量故障度为0.675 4。

4)对开关量时序信息进行约束检查，均满足时序约束关系。

5)对开关量时序信息进行挖掘分析，通过高斯函数计算，确定了基于开关量的时序模糊Petri网模型的初始置信度m0=(0.9，0.896 8，0.896 0，0.2，0.2，0.2，0.2，0.2，0.2，0.2，0.867 5，0.881 8)，由矩阵形式的模糊推理，经4次迭代计算，得到模糊故障度0.836 4。

6)对各故障度进行归一化处理，形成待融合证据体。

7)对待融合证据体利用D-S证据理论进行决策层融合，得到各元件最终的故障概率，如表1所示。

表1 诊断结果Table 1 Diagnosis results

从表1可判断元件L4-14发生故障，诊断结果与预设故障一致，所提方法能正确诊断出故障元件。在未考虑电气量的情况下，只针对开关量分析得到L4-14的故障概率仅为0.836 4，计及电气量和开关量综合分析得到的故障概率为0.919 4，故障概率显著地提高。

为进一步验证所提方法的有效性和容错性，还应充分考虑各种故障场景。表2为考虑各种复杂故障场景下的诊断结果，算例1模拟的是远后备保护及其相应断路器误动的故障场景，该方法能对断路器拒动和远后备保护误动有较好的容错性；在算例2中，模拟了近后备保护及其相应断路器误动的故障场景，仍能正确诊断故障元件；算例3中，虽然在主保护相应断路器时标信息错误且远后备保护信息丢失的复杂故障场景中，但仍不影响故障元件的正确诊断。在各个复杂故障场景中，仅对开关量分析得到的故障概率均低于综合分析电气量和开关量得到的故障概率，说明综合考虑电气量和开关量的电网故障诊断方法能有效地提高实际故障元件的故障概率，使故障诊断结果更加符合实际情况。

表2 新英格兰10机39节点系统的故障结果Table 2 Fault results of New England 10 machine 39 bus system

表3为本文所提方法诊断结果与文献[12]方法诊断结果的对比，经过多组仿真算例验证，本文所提方法能有效地提高实际故障元件的故障概率，并使非故障元件的故障概率大大地降低，具有更优的故障辨识能力。

表3 与文献[12]的对比结果Table 3 Fault results of New England 10 machine 39 bus system

5 结语

针对现有基于Petri网的电网故障诊断方法大多未考虑电气量且未有效地利用开关量时序信息的关联特性和冗余性的问题，本文提出了一种计及电气量和开关量的电网Petri网故障诊断方法。首先对元件的电流波形进行HHT分析，提取故障特征，通过模糊逻辑分析得到频率故障度和能量故障度。然后对开关量时序信息进行时序约束检查，剔除不满足时序约束的错误信息，利用时序关联特性确定事件的初始置信度，经模糊推理计算得到模糊故障度。最后利用D-S证据理论进行信息融合，得到元件最终的故障概率。多组仿真结果表明所提方法均能正确诊断实际故障元件，可见具有较好的准确性和容错性。