基于特征检测量的XLPE电缆绝缘老化寿命预测方法
2022-04-11李登淑吴健儿姚广元
李登淑,王 昕,吴健儿,赵 明,姚广元
(1.上海电力大学电气工程学院,上海 200090;2.上海交通大学电工与电子技术中心,上海 200240;3.国网浙江省杭州供电公司电缆运检室,浙江 杭州 310000)
与油纸绝缘及乙丙橡胶电缆相比,XLPE电缆具有性能优良、敷设简单、方便检修等优点,被广泛应用于10~220 kV的电网中[1-3]。而当前许多现役XLPE电缆敷设已有十几年,很容易发生绝缘老化甚至绝缘击穿问题,引起不可预计的损失[4-5]。因此,对XLPE电缆绝缘状态检测量进行相关测试,预测其绝缘老化剩余寿命具有重要的实际意义。
目前对电缆老化寿命的预测,大多采用电老化、热老化等加速老化试验,但这种方法周期长、成本高,不适用于快速及时地反馈绝缘寿命的需求[6]。文献[7-8]分别提出基于电特性、基于等温松弛电流法的XLPE电缆绝缘老化寿命评估,较充分地阐述了各性能对绝缘老化的影响,但由于是从理化微观角度进行研究,故其存在试验操作复杂且数据不易获取等问题;文献[9-10]提出利用冲击电压下电缆的等效电阻或测量有功损耗来预测老化寿命,可以实现基本的预测参考,但预测标准过于简单,导致预测结果可靠性差。近些年,随着对数据信息挖掘领域的研究,文献[11]利用RBF神经网络模型预测矿用电缆老化寿命,但常因为数据样本小,使模型出现饱和过拟合的问题;文献[12-13]分别建立了偏最小二乘(partial least squares, PLS)预测模型及最小二乘支持向量机(least squares support vector regression machine, LSSVR)预测模型;文献[14]针对变压器油纸绝缘建立了多输出支持向量回归模型,均取得了较好的预测结果。其中,PLS模型包含了主成分分析、典型相关分析等经典算法,是一种实用且简洁的数据处理手段,但由于其变量间的相关性或滞后变量的存在,使得模型出现多重共线性的问题,导致预测精度下降。
针对上述问题,本文对XLPE电缆绝缘状态进行检测,并通过对各检测数据的方差分析,选取了多个特征检测量用于标识电缆老化时间,提出了基于电缆绝缘老化特征检测量的偏最小二乘预测方法。考虑到运检数据样本少以及现有的数据处理方法存在适应性的问题,引入LSSVR来优化PLS模型主成分得分向量,提高模型的非线性处理能力,建立了基于特征检测量的XLPE电缆绝缘老化时间LSSVR-PLS预测模型。应用表明:改进后的模型在老化时间小样本数据处理中有着较高的预测精度,模型的泛化能力和数据预测适应性得到了很好的提高,对电网改造及电缆的运维工作具有实际指导意义。
1 电缆绝缘老化特征检测量的选取
影响电缆绝缘老化的因素很多,至今没有统一的评判标准,也很难回答哪些具体的参量可以用来对绝缘老化进行定量分析[15]。但现有的研究表明,电缆老化程度多取决于绝缘材料的电、热以及物理等性能,因此本文设计了对XLPE电缆绝缘状态的检测项目,通过对状态检测量的统计分析来确定表征电缆绝缘老化的特征检测量,以实现电缆绝缘寿命预测的目的。
1.1 绝缘状态检测项目
基于杭州供电公司送检的近20年内的45根110 kV XLPE电缆样品为检测对象,所有电缆的现场运行环境相近。选取老化时间不同其余条件均相同的5个电缆样品进行检测项目分析,电缆样品的采样区段均为不受外力破坏的正常运行老化区段,其中所选取的样品基本信息如表1所示。
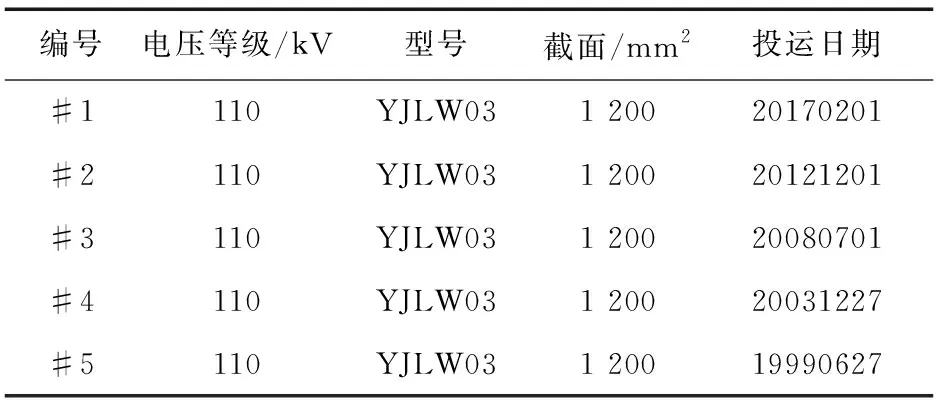
表1 取样电缆样品信息Table 1 Sample cable sample information
考虑到电缆绝缘存在径向不均匀性,因此采取环切取样方式,环切后的待测试样如图1所示。每个样品制备10份试样,以便多次取样求取检测结果平均值。

图1 环切后的电缆试样Figure 1 Cable sample after circumcision
1)拉伸测试。取环切电缆绝缘中层试样,厚度为1 mm,再进一步加工成标准哑铃状样条,如图2所示。采用型号为5KNCMT-4503拉力机,依照国标GB/T 1040—2006对XLPE试样进行拉伸试验,拉伸试验速率为100 mm/min,获取试样的拉伸强度和断裂伸长率。

图2 标准拉伸样条Figure 2 standard tendon spline
2)热重分析(thermal gravimetric analyze, TG)。采用AG 135型光电天平称量6 mg电缆试样,使用TG/SDTA 851e型热重分析仪测试XLPE的热分解行为。升温范围为50~600 ℃,升温速率为10 ℃/min,分析所得试样质量随温度的变化规即为TG曲线,从TG曲线中可提取热分解温度等参数。
3)差式扫描量热测试。采用Mettler DSC 822e型差式扫描量热仪测量XLPE电缆绝缘的熔融、结晶参数。在N2气氛中,将6 mg的XLPE试样从30 ℃加热至150 ℃,再将试样从150 ℃降温至30 ℃,升降温速率为10 ℃/min。为消除XLPE试样经历的热历史及试样中内应力等因素对测量结果的影响,对XLPE试样进行2次扫描,2次扫描时升温曲线的熔融峰对应的峰值温度即为熔融温度。
4)FTIR光谱测试。采用Nicolet iN10型傅里叶红外(FTIR)光谱仪对XLPE试样进行化学结构分析,测试模式为衰减全反射模式,测量的波数范围为4 000~500 cm-1,扫描次数为32次。波数在1 700~1 800 cm-1的吸收峰面积与1 460 cm-1的吸收峰面积比定义为羰基指数,并以此来定量分析电缆绝缘的氧化程度。
5)交流击穿场强测试。采用国产HJC-100 kV型电压击穿仪对XLPE试样进行工频击穿实验,击穿电极采用球—球电极,电极直径为25 mm,试样厚度为0.5 mm,测试温度为室温,升压速率为2 kV/s,同时将试样浸没在变压器油中以避免放电的产生。研究表明击穿电压的概率以及相关的数据,可采用二维威布尔(Weibull)分布进行处理分析,即
(1)
式中Eb为交流击穿场强,kV/mm;F为材料在场强E下的击穿概率;α为尺寸参数,kV/mm,其值反映击穿概率为63.2 %时的击穿场强;β为形状参数,其大小反映分散程度,β越小击穿场强分散性越大。
将式(1)变换为
(2)
由式(2)可知,若试验数据服从两参数Weibull分布,则等式的左边与lnEb为线性关系,斜率为β,截距为-βlnα。为得到较科学的计算结果,击穿概率F采用Ross分布函数,即
(3)
式中i为击穿测试数据排列的序号,i=1,2,…,n;n为击穿测试样本总数。
击穿场强由小到大进行编号,通过式(3)可求得相应编号下试样的击穿概率F,将F代入式(2)求得尺寸参数α,其数值即为计算所得击穿场强。
6)XRD扫描测试。根据XLPE试样其结晶相会在X射线衍射图谱中产生2个较尖锐的结晶峰,无定形相会产生一个较弥散的非晶峰的特点,采用D8 ADVANCE型XRD衍射仪对XLPE电缆绝缘试样进行XRD扫描,扫描速率为10°/min,步长为0.02°,扫描范围为15~30°,采用Cu靶辐射,工作电压40 kV,以此可获取结晶度的测试值。
基于上述XLPE电缆样品绝缘状态检测项目,对应提取了拉伸强度、断裂伸长率、热分解温度、熔融温度、羰基指数、交流击穿场强以及结晶度共7个参量,这些参量从不同层面反映了电缆绝缘老化状态的特性。
1.2 选取特征检测量
利用数理统计方法对上述老化电缆样品的各检测数据平均值进行单因素方差分析,取显著性差异水平α=0.05,则Fα=4.28,计算得到不同样品同一参量的检验统计量F0分别为103.97、69.31、76.29、265.34、99.87、121.44、85.21。均存在F0>Fα,说明对于不同老化时间,上述每一个参量均是显著不同的。因此,可选取这些参量作为特征检测量对不同老化程度的电缆进行标识,如图3所示。
图3 不同特征检测量指标Figure 3 Different feature detection indicators
根据所测试的特征检测量,为实现电缆绝缘老化时间的综合性预测,使模型中同时包含所有的特征检测量,本文建立了老化时间关于特征检测量的多元线性PLS预测模型。但考虑到变量之间的相关性或滞后变量的存在均会使模型产生多重共线性问题,在数据样本有限的情况下,为增强模型的有效性,本文引入了学习能力强、泛化性高的LSSVR,其具有解决非线性对应关系的优点,并以此建立LSSVR-PLS电缆绝缘老化时间预测模型。
2 XLPE电缆绝缘老化时间预测模型
2.1 PLS算法
PLS回归分析是一种实用且简洁的统计数据处理方法,其算法内容包含有主成分分析、典型相关分析和多元线性回归分析。其基本的算法原理可参考文献[13]。
2.2 LSSVR算法
LSSVR支持向量回归机是对SVR的一种改进,主要区别是把原支持向量机中的不等式约束变成了等式约束,简化了Lagrange的求解过程,使最终的求解变为一个解线性方程组的问题。同时,相较于PLS算法在小样本应用时存在的多重共线性问题,LSSVR算法可对PLS内部主成分得分向量进行优化,以提取变量有用信息降低或消除变量与因变量之间的非线性对应关系。
设给定的k个样本数据{ti,yi}(i=1,2,…,k),其中ti为输入,yi为输出,则利用LSSVR进行成分优化模型如下。
目标函数为
(4)
等式约束条件为
yk=wTφ(tk)+b+ek
(5)
式(4)、(5)中e为松弛因子;γ为惩罚因子;b为偏置项;w为特征权向量;yk为样本输出;φ(tk)为非线性映射函数;k=1,2,…,N。
采用Lagrange乘数法求解,即
L(w,b,e;α)=
(6)
进一步推导有:
(7)
最后化简为
(8)
其中,Ωkl=φ(tk)Tφ(tl)=K(tk,tl),k、l=1,2,…,N,被称作核矩阵。
由上述线性方程组可求得LSSVR优化模型为
(9)
2.3 基于LSSVR优化的PLS算法模型
设p个变量y1,y2,…,yp为因变量集,m个自变量x1,x2,…,xm为自变量集。为了表达方便和减少变量之间的运算误差,首先对因变量集和自变量集进行标准化处理。F0与E0分别为二者的n次标准化观测数据阵,即
(10)
(11)
考虑到本文基于老化时间的XLPE电缆绝缘老化寿命预测问题,因变量集为单一变量即老化时间,而自变量集为不同的特征检测量,因此只对自变量集进行处理分析,即直接在E0,E1,…,Er-1矩阵中提取成分t1,t2,…,tr(r≤m)。要求th(满足有效性检验要求的主成分,h≤r)尽可能多地携带E0中的信息,同时对因变量系统F0有最大的解释能力。建模步骤如下。

4)根据交叉有效性,提取到h个满足要求的主成分得分向量,改变以往偏最小二乘直接建立F0与τh回归方程的方式,建立文2.2节中提到的LSSVR优化的主成分模型,即
(12)
式中y0(τh)为样本标准化输出;K(τh,τk)为核函数,其参数由样本数据训练得出。
5)采用原始数据表示,首先计算训练样本成分的得分向量为
(13)
然后,根据因变量集Y计算回归模型中的参数向量ch=YTτh/‖τh‖2,并将式(12)记为y0=fLSSVR(τh)。最后得到原始数据的LSSVR-PLS预测模型为
(14)
2.4 相关参数的确定
模型中包含的参数[α,b],即拉格朗日乘数和偏置项可由式(7)进行求解。其次,由于PLS模型存在多重共线性问题,故核函数选择有利于弱化非线性对应关系的RBF径向基核函数为
(15)
式中σ为核宽度大小。惩罚因子γ和核宽σ对LSSVR模型精度有较大的影响。γ越小,模型泛化能力越强,但误差相对增大;σ越小,模型学习能力越强,但复杂度增高。
因此,本文将实验所得的老化特征检测量数据分为训练样本和测试样本,在VS2013环境下利用Matlab R2013a中的支持向量分类工具箱对训练样本进行迭代分析,并根据误差RMSE来确定γ和σ值。经过反复迭代对比,二者与误差RMSE对应变化趋势如图4、5所示。

图4 参数γ与RMSE的对应变化趋势Figure 4 Corresponding trends of γ and RMSE
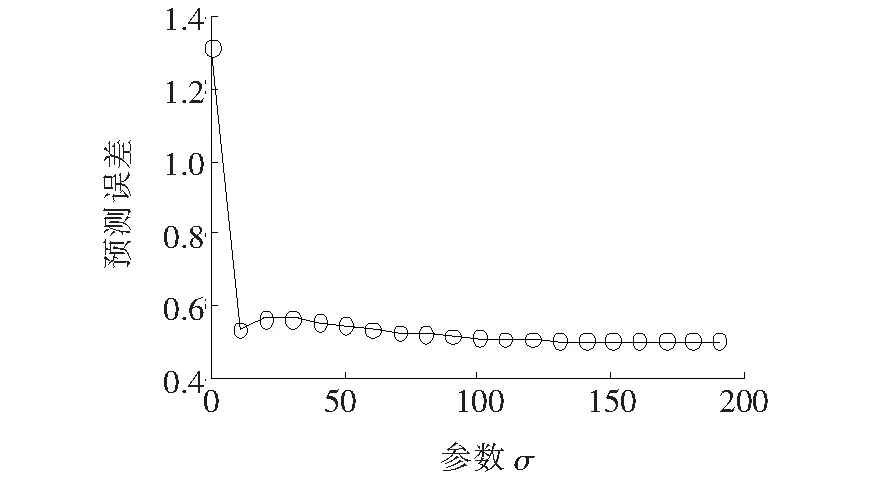
图5 参数σ与RMSE的对应变化趋势Figure 5 Corresponding trends of σ and RMSE
根据图4、5中RMSE存在的极小值点选择正则化参数惩罚因子γ=20,核宽σ=10。
3 算例分析
3.1 试验数据
将相同的电缆样品,根据老化时间的不同分为15组,相同的采样区段下每组制备5份试样(忽略外力破坏、同一区域环境差异大的因素)。每组特征检测量数据均取为5份试样的平均值,选用前2/3数据为训练样本,后1/3数据为测试样本。按老化时间从小到大排列,各组特征检测量的平均测试数据如表2所示,其中带“*”的用于模型测试。
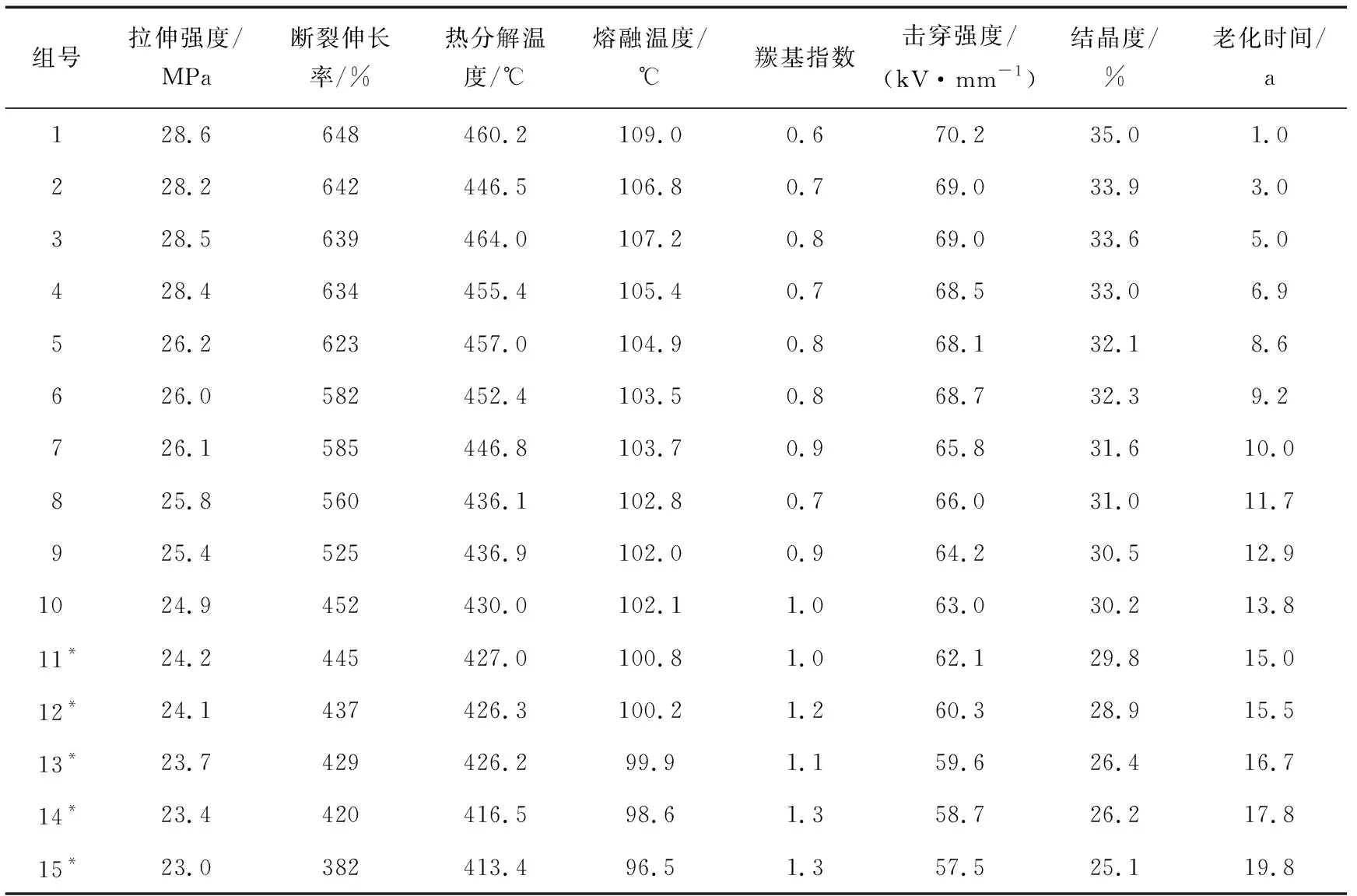
表2 各组电缆样品特征检测量数据Table 2 Data test data of each group of cable samples
3.2 相关性分析
将表2的各检测量依次记为:C1、C2、C3、C4、C5、C6、C7以及老化时间Y,利用逐步回归分析对特征检测量与老化时间之间的线性相关性进行检验,所得的残差如图6所示。
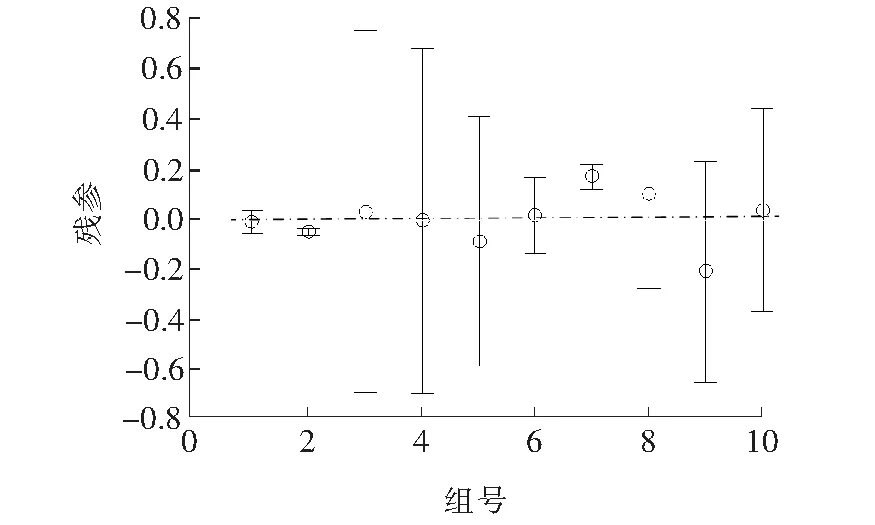
图6 残差杠杆Figure 6 Residual lever diagram
由图6可知,第2、7组线性拟合较差,其余线性拟合良好。整体的线性拟合度R2=0.994 3,在F检验中,统计量F=131.897 8>0.000 0,符合检验要求。但根据图6所求得的与显著性概率相关的P值为0.443 4>0.05,说明变量系统中存在着多重共线性问题,若直接采用PLS建立多元线性电缆绝缘老化时间预测模型,精度可能会大大地降低。
3.3 建立LSSVR-PLS老化时间预测模型
首先,利用训练样本进行PLS线性回归分析,根据交叉有效性检验提取到2个主成分。
第1个提取成分得分向量为
τ1=
[-3.643 -1.951 -2.235 -1.643 -0.356 0.168 1.180 1.459 2.864 4.158]
第2个提取成分得分向量为
τ2=
[0.572 0.666 -0.005 -0.244 -0.757
-0.657 -0.151 -0.212 -0.017 0.805]
建立电缆绝缘老化寿命PLS预测模型,即
Y=
141-0.274 1x1-0.003 0x2+0.057 8x3-
0.845 4x4-3.352 0x5-0.246 8x6-1.294 1x7
(16)
利用LSSVR对上述2个主成分得分向量行优化,由式(12)可得优化后的成分向量为
τ′1=
[3.635 1.938 2.239 1.653 0.369 -0.157
-1.179 -1.454 -2.865 -4.177]
τ′2=
[0.590 0.626 0.032 -0.141 -0.835
-0.738 -0.203 -0.167 0.005 0.831]
则由式(13)、(14)可得LSSVR-PLS老化时间预测模型为
Y′=
117-0.475 0x1-0.003 3x2+0.010 5x3-
0.569 1x4+1.920 0x5-0.223 2x6-0.799 5x7
(17)
3.4 模型检验及训练结果
采用回归参数T检验法分别对式(16)PLS和式(17)LSSVR-PLS老化时间预测模型进行多重共线性检验。变量系数检验为T检验值,线性回归效果检验为F检验值,检验结果分别如表3、4所示。
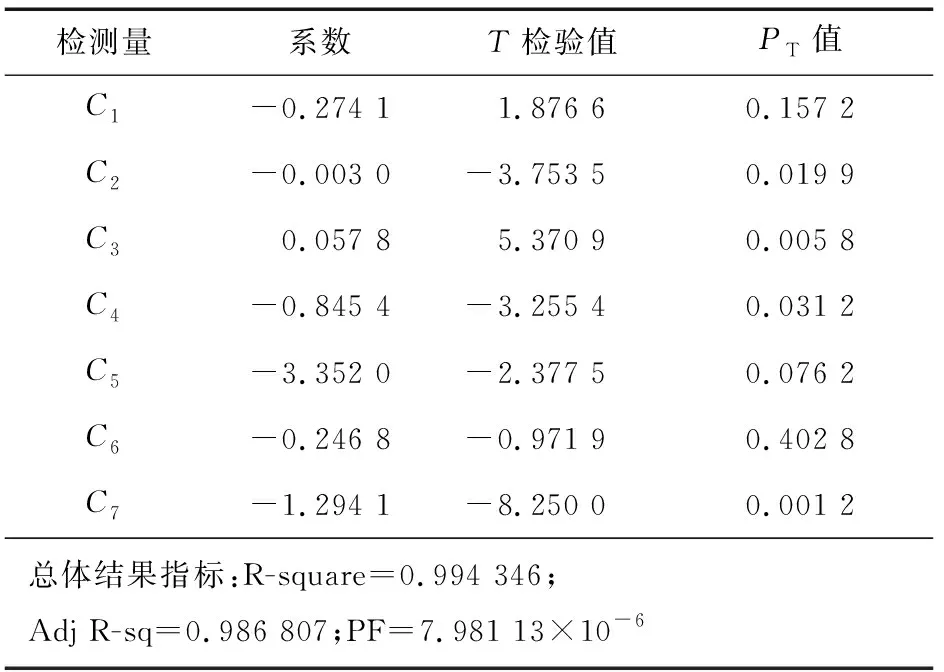
表3 PLS模型多重共线性检验结果Table 3 PLS model multi-collinearity test results
由表3、4可知,2种模型均满足F检验,模型的线性拟合度较好。由表3可知PLS模型中特征检测量C1和C6系数的T检验值PT>0.1,不满足检验显著性要求;而由表4可知,LSSVR-PLS模型中系数的T检验值PT<0.1,满足检验显著性要求。此时可认为后者基本消除了数据间的多重共线性问题,其训练样本的结果输出曲线及相对误差分别如图7、8所示。

表4 LSSVR-PLS模型多重共线性检验结果Table 4 LSSVR-PLS model multicollinearity test
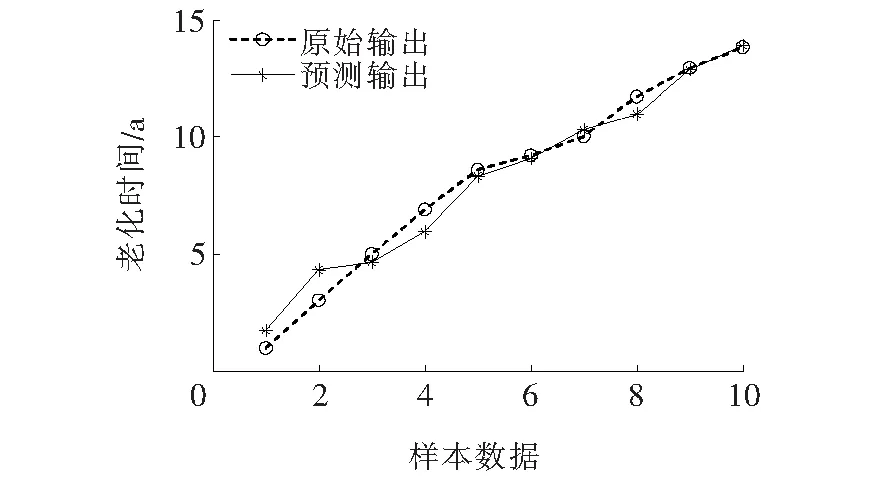
图7 LSSVR-PLS模型训练结果Figure 7 LSSVR-PLS model training results
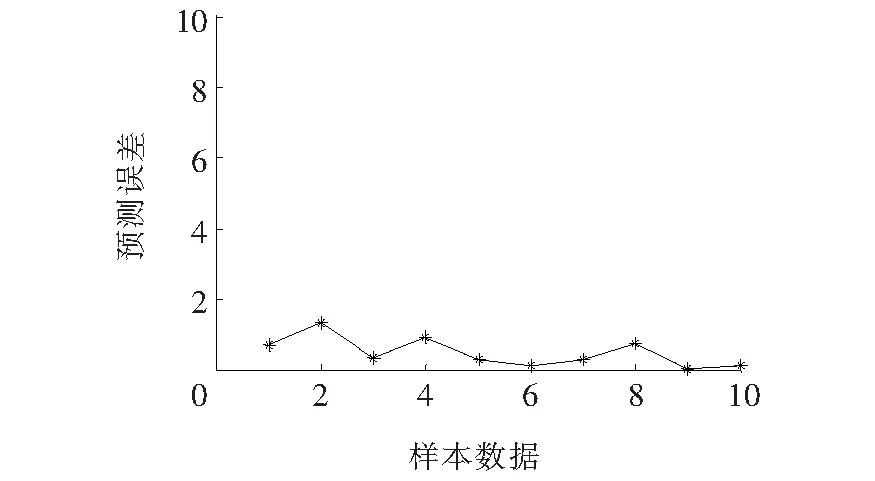
图8 LSSVR-PLS模型训练结果误差Figure 8 LSSVR-PLS model training result error
从图7、8模型训练结果上看,预测输出与原始输出误差较小且相对稳定,说明改进后的预测模型效果好、精度高,同时也说明了LSSVR-PLS模型预测电缆老化时间具有较强的适应性。
3.5 预测精度分析
现以表2中带有“*”的各检测量数据进行测试,本文分别采用LSSVR-PLS模型、PLS模型、LS-SVM分类模型以及RBF神经网络模型对测试样本数据进行预测,预测结果如图9和表5所示。
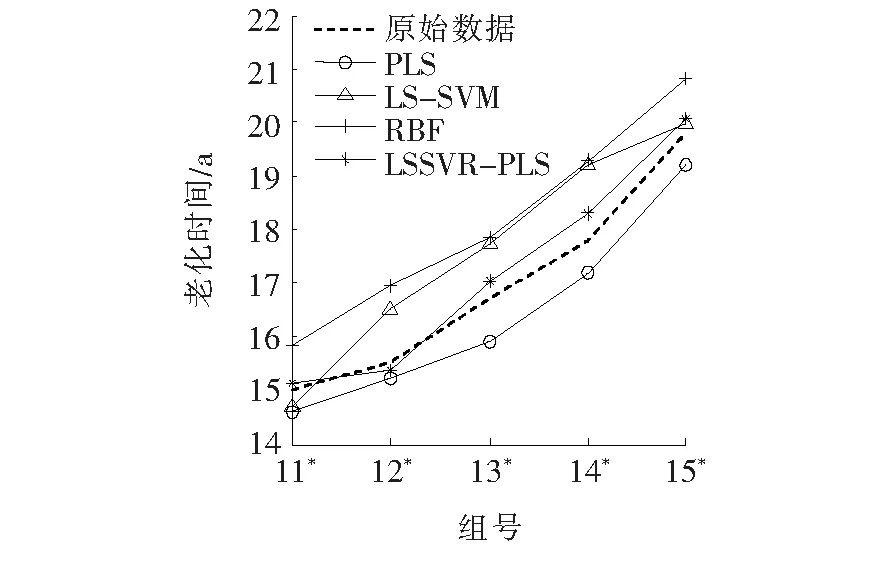
图9 4种模型预测结果对比Figure 9 Comparison of prediction results of four models
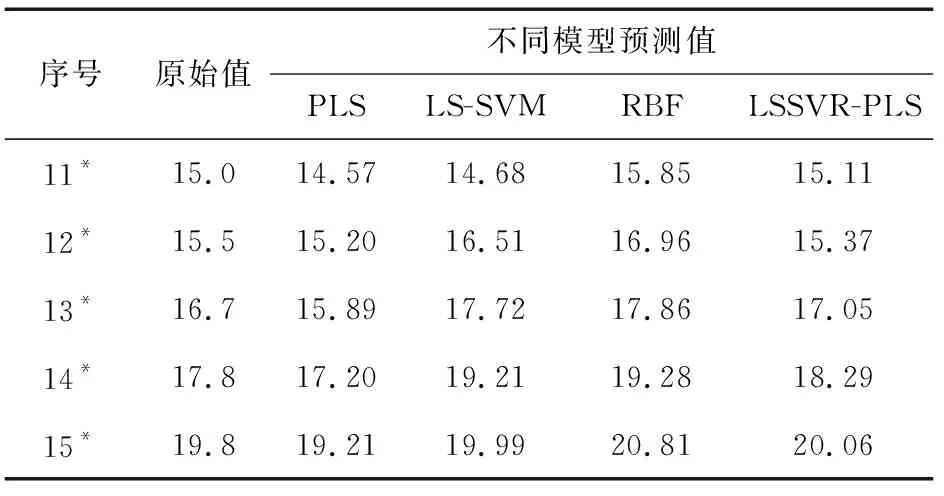
表5 4种模型预测值与实际值的比较Table 5 Comparison of predicted and actual values of four models
根据上述预测结果可得4种模型之间的相对误差如图10所示;各模型相对误差绝对值的平均百分数以及方差情况如表6所示。
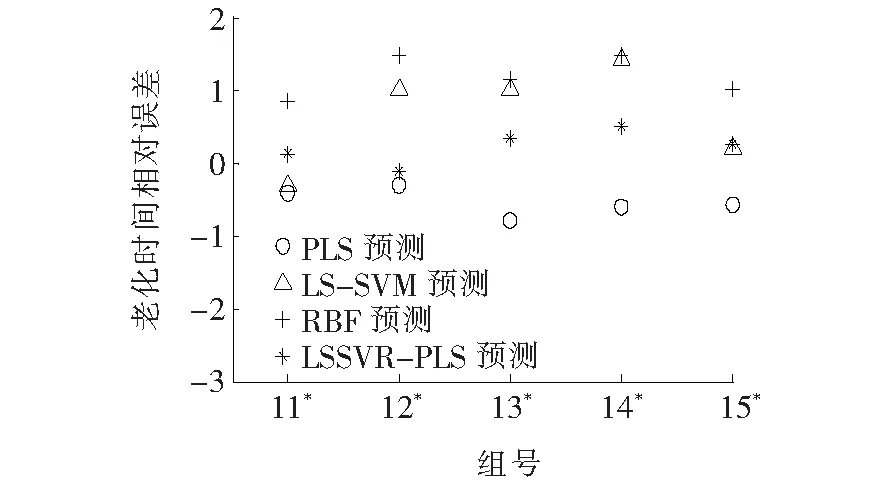
图10 测试样本老化时间相对误差Figure 10 Relative error of aging time of test sample
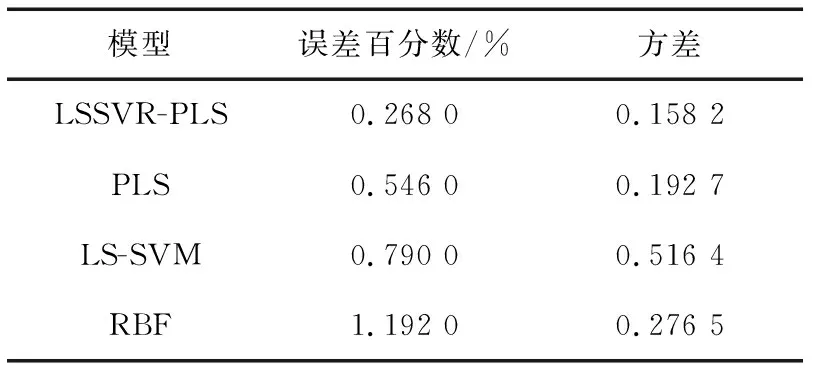
表6 相对误差绝对值平均百分数及方差Table 6 Average percentage and variance of relative error absolute value
根据上述计算可得,相比于在解决小样本问题容易过饱和的RBF神经网络预测,PLS和LS-SVM模型在电缆绝缘老化时间上误差更小、预测精度更高,而LSSVR-PLS预测精度要优于PLS和LS-SVM模型。其次从预测误差及误差稳定性来看,虽然RBF神经网络误差最大,但其误差稳定性较LS-SVM模型好,这与选取适于处理非线性的RBF径向基核函数有关。从整体对比来看,LSSVR-PLS模型解决了RBF神经网络小样本容易过拟合的问题,同时避免了LS-SVM分类模型过于依赖经验的盲目性以及PLS模型中存在的多重共线性问题,证明了其在电缆绝缘老化时间小样本预测问题上具有更强的泛化能力和数据预测适应性。
3.6 剩余寿命预测
为进一步预测剩余寿命,将上述建立的电缆绝缘老化时间LSSVR-PLS预测模型记为LSVR-PLS,那么将失效状态下的特征检测量带入LSVR-PLS中,可得电缆整体的老化寿命Lend,参考文献[16]建立电缆绝缘老化时间关系模型的思想,则电缆的剩余寿命Lremain=Lend-LSVR-PLS。表7为从绝缘失效电缆区段采样所测得的各特征检测量平均值。
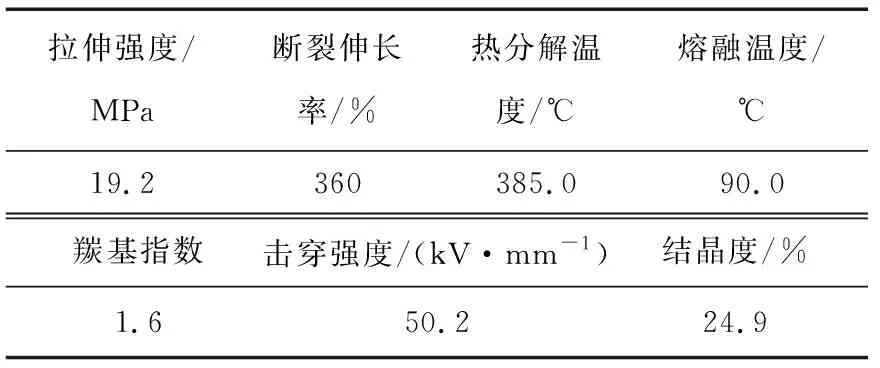
表7 失效电缆的绝缘特征检测值Table 7 Insulation characteristics of the failed cable
将失效数据带入LSVR-PLS中,计算Lend≈29.7 a,得到测试样本绝缘老化剩余寿命,如表8所示。
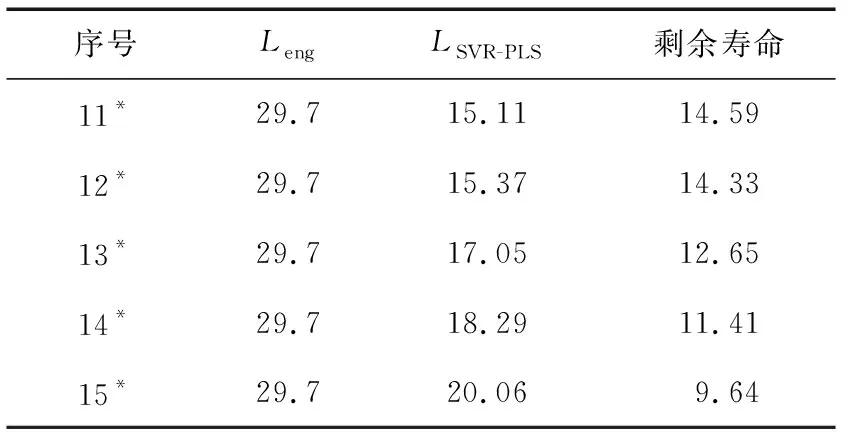
表8 基于LSSVR-PLS的电缆绝缘老化寿命Table 8 LSSVR-PLS based on-site aging cable insulation remaining life a
4 结语
1)本文对不同老化时间的电缆样品进行了一系列绝缘状态检测项目,提出了多个特征检测量用于标识绝缘老化程度,并对相应的检测数据进行方差分析,检验了各特征检测量的适应性。
2)根据所提出的特征检测量建立了电缆老化时间的LSSVR-PLS预测模型,该模型在小样本电缆数据处理过程中,具有适应好、泛化能力强和预测精度高的特点。并且避免了数据过拟合以及多重共线性问题,能够较快准确地实现XLPE电缆绝缘老化寿命的预测,对电缆的运维检修具有一定的指导意义。
3)由于实验条件及设备的限制存在有一定的局限性,电缆绝缘老化特征检测量的选取不能面面俱到,模型中忽略了环境差异性的影响等,这些方面也是今后要研究的方向,所需研究的内容将进一步提高模型对现场老化数据的解释能力。
