一种基于有限域乘法单群的公钥密码算法及实现*
2022-04-11江宝安
江宝安
(1.重庆移通学院,重庆 401520;2.重庆邮电大学,重庆 400065)
0 引言
1976 年,Diffie 和Hellman提出了密码交换概念,为公钥密码学提供了理论基础。1985 年,Elgamal[1,2]提出了一种公钥密码体制,其安全性基于求离散对数的困难问题上,是一种国际公认的较理想的公钥密码体制,是目前应用在保密通信和数字签名领域的有效的安全算法。ElGamal 公钥方案的提出是密码学的一个巨大的突破,是继安全性基于大整数分解的困难问题的RSA[3,4]算法提出后,又一个里程碑事件。
ElGamal 公钥密码体制是建立在有限域Zp上的,系统参数的选择受到一定的限制。本文提出一种建立在有限域乘法群上的公钥密码算法。p为素数,该乘法群的阶为2p-1,且为梅森素数,则该乘法群为有限单群。在此基础上的DH 公钥密码体制,其安全性也是基于求离散对数的困难的问题上,但是此离散对数是基于有限扩域上的,区别于ElGamal的有限域Zp。
本文算法继承ElGamal 公钥密码体制的优点,又有算法简单、参数选择灵活、计算速度快、执行效率高等优点,具有极大的理论和实际应用价值。
1 ElGamal 公钥密码方案
1.1 参数初始化
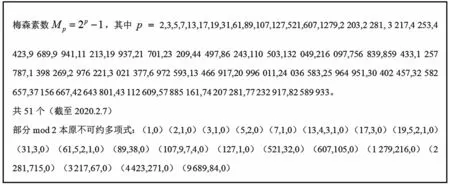
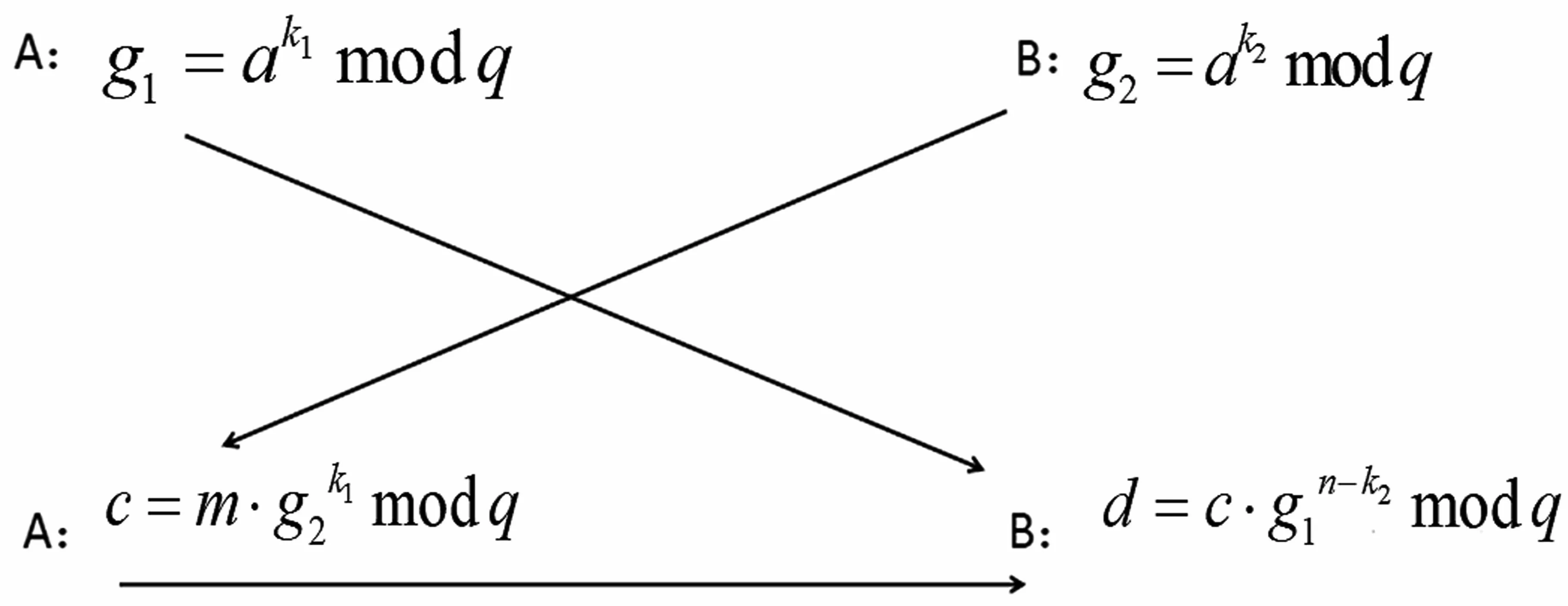
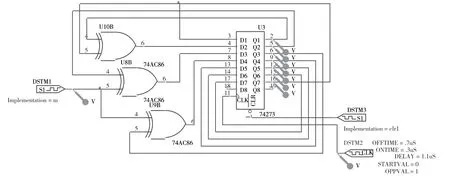
取大素数p,取p-1 阶生成元a∈,取随机数k1,0 (1)发送方A 随机选择数k1,0 本文提出了一种新的基于有限域乘法单群的公钥密码[5,6]。有限域的乘法群的阶为n=||=2p-1,p为素数且使得n=2p-1为梅森素数,具体取值如图1所示。则乘法群为有限单群,任何一个元素a∈的阶为n,即anmodq=1(q为p次不可约本原多项式),a+a=0。 图1 梅森素数及部分模2 本原不可约多项式 新算法的具体流程如下文所述。 p为素数且使得n=2p-1 为梅森素数,推荐p取521,1 279 或2 281,相应的p次不可约本原多项式为q=x521+x32+1,x1279+x216+1 或x2281+x715+1(x为多项式不定元)。随机取元素a∈(a≠1),则anmodq=1,(p,n,q,a)为公开的系统参数(若a不公开,破译难度更高)。发送方A 随机取私钥1 如图2 所示,发送方A 生成密文c=m·modq,接收方B 使用私钥k2解密: 图2 乘法公钥密码 笔者已经对该算法完成软硬件仿真验证,软件采用MATLAB 仿真,最高已验证p=9 689的加解密,可以转化成C 语言或者汇编语言等,并且可应用于不同的平台。硬件采用线性反馈移位寄存器实现,需要p个寄存器,所需时间为p个时钟周期,计算速度快。 取p=5,本原多项式q(x)=x5+x2+1,数组形式q(x)=[100101],随机选择a=x4+x2+1=[10101],=a 算法复杂度分析:模平方运算a2modq有快速算法,需要O(p)次比特运算,模乘a·bmodq运算需要O(p2)次比特运算,模幂ak·modq运算需要O(p3)次比特运算,整个加密解密最耗时的主要是模幂运算。当加密解密多项式已预先算出时,采用带反馈的移位寄存器可同时实现乘除运算即模乘运算,加密解密时间均为p个时钟周期。 3.2.1 硬件实现关键技术 加密硬件实现如图3 所示,当p个比特明文m串行输入结束后,p个寄存器的值即为密文;解密硬件实现如图4 所示,当p个比特密文c串行输入结束后,p个寄存器的值即为解密明文。加解密所需时间均为p个时钟周期。 图3 加密硬件实现(用移位寄存器和异或门) 图4 解密硬件实现(用移位寄存器和异或门) 3.2.2 实例 取p=7,本原多项式为q(x)=1+x+x7=[11000001],明文为m(x)=1+x+x4=[1100100],加密多项式为g(x)=x2+x3=[0011000],解密多项式为h(x)=x+x2+x3+x4+x6=[0111101],加密密文为c(x)=m(x)·g(x)modq=1+x+x2+x4+x6=[1110101],加密硬件实现如图5所示。 图5 实例2 中 p=7 加密硬件实现(用移位寄存器和异或门) 解密明文为d(x)=c(x)·h(x)modq=1+x+x4=[1100100]=m(x),解密硬件实现如图6 所示。 图6 实例2 中 p=7 解密硬件实现(用移位寄存器和异或门) 实例2 用移位寄存器和异或门的硬件实现的电路如图7 所示,仿真结果如图8 所示。 图7 实例2 具体加密硬件实现电路(用移位寄存器和异或门) 图8 实例3 具体加密硬件实现电路仿真波形 主程序以p=31 乘法加密解密为例,以下是MATLAB 源程序: 现有的典型的公钥密码算法如RSA、ElGamal和椭圆密码ECC 都有各自的优缺点,适应不同的应用场合,在多种文献中有详细的介绍和说明[7-14]。本文在有限域乘法单群的基础上,提出了新的公钥密码算法。该算法本身基于模2 运算,只需要用移位寄存器和异或门就可实现,不需要构建长整数运算,也不需要计算有限域原根[15],相较传统的ElGamal 和RSA 公钥算法具有系统参数选择灵活、计算速度快、安全性高等优点,具有广泛的理论和实际应用价值。1.2 加密过程
1.3 解密过程
2 一种新的基于有限域乘法单群的公钥密码
2.1 乘法型加解密
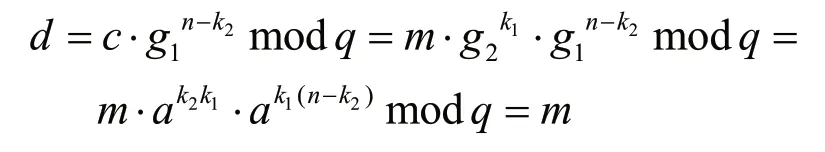
2.2 加法型加解密

3 算法实例
3.1 实例1

3.2 实例2






4 算法软件实现程序(MATLAB 仿真)
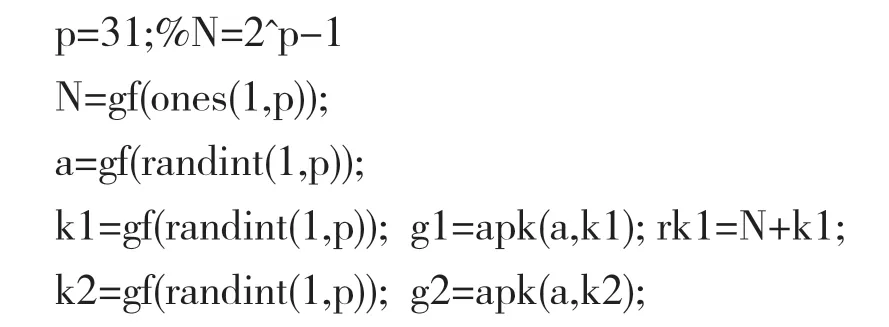


5 结语
