利用函数的对称性解决一类数列问题
2022-04-11四川省南充高中顺庆校区637002张小丹
四川省南充高中顺庆校区 (637002) 张小丹
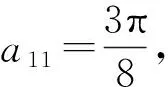
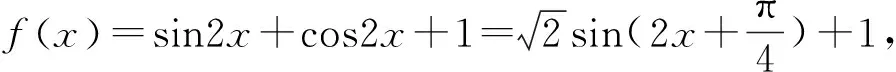
∴f(a1)+f(a2)+…+f(a21)=21.
由引例1的分析过程,我们不难得到如下结论.
结论1 设函数f(x)的对称中心是(a,b),且f(a)=b(即对称中心在函数图像上),数列{an}是等差数列,其中一项ak=a(对称中心的横坐标),则以ak为中间项的数列a1,a2,…,ak,…,a2k-1的函数值之和f(a1)+f(a2)+…+f(a2k-1)=(2k-1)b(项数×对称中心的纵坐标).
证明:∵函数f(x)的对称中心是(a,b),∴f(x)+f(2a-x)=2b.∵a1+a2k-1=a2+a2k-2=…=ak-1+ak+1=2ak=2a,∴f(a1)+f(a2k-1)=f(a2)+f(a2k-2)=…=f(ak-1)+f(ak+1)=2f(ak)=2b.
∴f(a1)+f(a2)+…+f(a2k-1)=(2k-1)b.
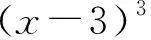
A.0 B.7 C.14 D.21
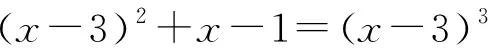
由引例2的分析,不难得到如下结论.
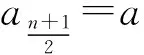
证明:不妨设f(x)在区间I上递增.∵f(x)的对称中心在f(x)上,∴f(x)+f(2a-x)=2b.假设a1+an≠2a,不妨设a1+an>2a,则a1>2a-an,∴f(a1)>f(2a-an)=2b-f(an),∴f(a1)+f(an)>2b,同理f(a2)+f(an-1)>2b,…,于是f(a1)+f(a2)+…+f(an)>nb与已知不合.故必有a1+an=a2+an-1=a3+an-2=…=2a.
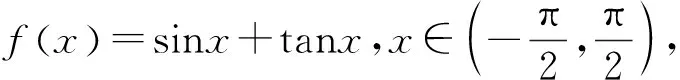
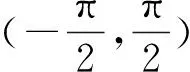
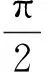
分析:易知f(x)图像的对称中心是(0,2)且f(x)是增函数,∵sina1+a1+sina3+a3+sina5+a5+sina7+a7+sina9+a9=0,∴f(a1)+f(a3)+f(a5)+f(a7)+f(a9)=10,由结论2知中间项a5=0,∴a3=-π,∴f(a3)=f(-π)=2-π.
例3 (2021衡水中学测试)已知等差数列{an}的公差为2020,若函数f(x)=x-cosx,且f(a1)+f(a2)+…+f(a2020)=1010π,记Sn为{an}的前n项和,则S2020的值为( ).
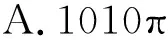
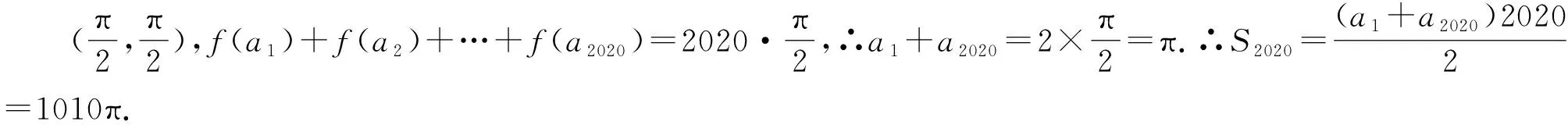
巩固练习:
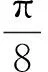

A.S2016=-2016,a2013>a4B.S2016=2016,a2013>a4
C.S2016=-2016,a2013 A.4030 B.4028 C.2015 D.2014 答案提示:1.D;2.D;3.C