基于距离代价的自适应惯性权重粒子群优化算法

黄欣 丘刚玮 唐伟萍

摘要：由于不同等级种群的学习能力不一样，其步长大小也会不一样，该文提出了一种新的基于距离代价的自适应惯性权重粒子群优化算法。该算法在运行过程中根据粒子位置的距离代价，将种群分为三个等级，对不同等级的种群采用不同的惯性权重策略更新粒子的速度和位置，并在每次迭代的过程中对全局最优加入一个扰动因子来增加粒子的多样性。通过仿真实验，将该文提出的PSO算法与其他几种粒子群优化算法进行对比，实验结果表明：在相同条件下该算法能以较少的迭代次数得到最优解，同时兼具好的收敛速度和高的收敛精度。

关键词：粒子群优化算法;自适应惯性权重;粒子距离代价;DCAPSO;扰动因子

中图分类号：TP391        文献标识码：A

文章编号：1009-3044（2022）05-0052-04

1 引言

粒子群优化算法[1]（Particle Swarm optimization，PSO）是一经典的群智能演化算法，在1995年由Eberhart和Kennedy提出。PSO算法因其快速收敛、易于实现、鲁棒性好等优势优点，被广泛研究以及改进。改进的领域有故障检测[2]、医疗诊断[3]、科学管理[4]、飞行器协调跟踪优化[5]等。尽管PSO的优势突出，在实际应用中逐渐暴露其后期迭代收敛差、容易陷入局部最优值且难以跳出、收敛精度低的缺点。越来越多的学者致力于对PSO进行优化改进。Shi等人提出w是极其重要的一项参数，先后提出随机权重（Random Weight，RW）[6]、线性递减权重（Linear Decrease Weight，LDW）[7]和模糊惯性权重[8]这三种策略。以上三种惯性权重的改进策略，实际上通过自适应调节惯性权重的大小，进而控制粒子的局部和全局搜索能力，即惯性权重越大，该粒子的全局搜索能力越强;惯性权重越小，粒子的局部搜索能力越大。上述三种策略提高了粒子群的整体性能和收敛速度。文献[9]分析了对惯性权重改进的几种典型策略，如：非线性型函数、高斯分布型函数、正弦分布型函数等。

以上的改进策略在一定程度上提高了PSO算法的性能，但是等级不同的种群学习能力不一样，因此步长大小也会不一样。上述的改进算法未能解决在不同等级的种群自动调节步长大小的问题。为了解决该问题，本文提出了新的PSO算法。该算法采用粒子的距离代价将种群划分为三个不同的等级，并针对等级不同的粒子采取相应的惯性权值策略来更新粒子当前的速度和位置，在每次迭代的过程中对全局最优加入一个扰动因子，并融入了“pbest和gbest线性组合”思想使算法在很大程度上克服了收敛慢、易陷入局部等缺点，且获得了较好的优化效果。

2 标准的粒子群优化算法

标准的PSO算法是根据以下公式更新粒子的速度和位置：

vi（t+1）=wvi（t）+c1r1（pbesti（t）-xi（t））+c2r2（gbesti（t）-xi（t））         （1）

xi（t+1）=xi（t）+vi（t+1）                                 （2）

其中，w为惯性权重;t为当前的迭代次数;r1和r2是在随机数，随机范围为[0，1];c1和c2是学习因子;vi（t）为粒子i在t时刻的速度;xi（t）为粒子i在t时刻的位置。

针对基本PSO算法收敛速度缓慢、极易陷入局部最优这些缺点，Shi等人分别在文献[6-7]提出RW、LDW策略，还有研究者提出“非线性型函数”策略。这三种策略的更新公式分别为：

[ w=0.5+rand（）2]                        （3）

[w=wmax-t*（wmax-wmin）tMax]                    （4）

[w=wmin+（wmax-wmin）*exp（-25*（ttMax）6）]                   （5）

以上算法均是從算法本身的收敛特点来对惯性权重的大小进行调整，即在算法迭代初期时，粒子群需要较强的全局搜索能力，进行更加全面的全局搜索;在算法搜索后期时，粒子群需要更强的搜索能力，以便使得算法加快收敛。但是，并没有根据种群实际搜索情况对种群分等级，并采取不同的搜索策略。

3 基于距离代价的PSO算法

3.1 距离代价

由于不同等级的种群学习能力是不一样的，其步长也是不一样的。通过对不同等级的种群采用不同的搜索策略，使得等级不同的种群自适应调整步长的大小，更好地适应实际的搜索情况，能够在局部搜索与全局搜索之间进行有效的平衡。我们通过采用“距离代价来”将粒子群划分成三个不同的种群。“距离代价”这一概念在2006年提出[10]，它作为最佳聚类数的有效性检验函数去解决K-means 算法的k值优化问题。

根据粒子群优化算法的特点，本文重新构造如下的距离代价函数：

定义1：令avg（xi（t））为粒子i在t时刻所有维度上的平均位置，avg（gbesti（t））为此时全局最优在所有维度上的平均位置。定义此时两者的位置距离为：

L（t）=| avg（xi（t））- avg（gbesti（t）） |                 （6）

定义2：令avg（pbest（t））为所有粒子在t时刻个体最优的平均位置。定义此时avg（xi（t））与avg（pbest（t））的位置距离为：

D（t）=| avg（xi（t））- avg（pbesti（t）） |             （7）

定义3：定义粒子的“距离代价”为L（t）与D（t）相加之和：

F（L，D）= L（t）+D（t）                  （8）

本文确定了距离代价最小准则作为衡量粒子的优劣性，即：当距离代价最小时，粒子所处的位置最优。

3.2 自适应惯性权重

惯性权重w是平衡该算法全局探索能力与局部开发能力的关键因素。取较大的w时，粒子具有较强的全局搜索能力;反之，具有较强的局部搜索能力。

本文的改进策略如下：在第t次迭代中，用公式（6）（7）（8）计算每个粒子的距离代价Fi（L，D），将距离代价进行升序排序，然后将它们分成两半分别计算平均值F_avg1和F_avg2，最后将每个粒子的距离代价Fi（L，D）与F_avg1、F_avg2进行比较，从而将粒子群分成三个等级的子群，对不同等级的子群采用以下三种不同的惯性权重w策略：

Fi（L，D）<F_avg1：此时是较好的粒子，并处于距离gbest或pbest相对较近的位置，此时应取较小的惯性权重wmin。

Fi（L，D）>F_avg2。说明此时该粒子是较差的粒子，并处于距离gbest或pbest相对较远的位置，此时应取较大的wmax。

Fi（L，D）>F_avg1且Fi（L，D）<F_avg2。此时，w在[0.4，0.6]范圍内随机取值。

3.3 DCAPSO算法

均值粒子群优化算法（Mean Particle Swarm Optimization，MeanPSO）最初是由Kusum Deep等[11]在2009年提出，使用pbest和gbest的线性组合来修正pbest、gbest，该算法的速度更新公式为：

vi（t+1）=wvi（t）+c1r1（（pbesti（t）+gbesti（t））/2- xi（t）） +c2r2（（pbesti（t）-gbesti（t））/2-xi（t））  （9）

综合上文，本文提出了基于距离代价的自适应惯性权重粒子群优化算法（an Adaptive inertial weight Particle Swarm Optimization algorithm based on Distance Cost，DCAPSO）。

算法设计思路是：通过设计代价距离函数，将粒子种群划分为三个不同等级的子种群，然后子种群根据他们距离食物不同的位置，采取不同的搜索策略，使其自适应选择不同的惯性权重，进而自动调整搜索步长，以达到平衡局部搜索和全局搜索的效果。

DCAPSO的主要技术要点和操作步骤如下：

Step 1：初始化粒子种群，即初始化gbest0、pbest0、速度v0、位置x0、学习因子c、惯性权重w0;

Step 2：评价每个粒子xi的是适应度值f（xi），即计算对应的目标函数值;

Step 3：更新pbest——将历史中的个体位置记录为{p0，p1，...，pn}，其中适应度值最优的粒子个体即为pbest;更新gbest——将每一代的个体最优记录为{pbest0，pbest1，...，pbestn}，假设第i个个体最优的适应度函数值最优，则pbesti即为gbest;

Step 4：不同的粒子采用3.2不同的w更新策略，粒子根据三种不用的更新策略，划分成三个子种群，每个子种群具有不同的功能：第一个子种群处于个体最优或者全局最优个体的附近，需要对此处进行更加详细的局部挖掘，因此采用较小的惯性权重;第二个子种群距离最优个体较远，说明该处有食物的概率较小，需要对该处进行更加详细的全局搜索，因此使用较大的惯性权重;第三个子种群处于前两者之间的位置，需要平衡局部和全局搜索，因此需要适中的惯性权重;并使用公式（2）（9）更新粒子的速度和位置;

Step 5：对全局最优gbest施加一个服从正态分布的扰动因子gbest=gbest*μ，其中μ=0.5*normrnd（0，1）;

Step 6：判断是否终止迭代，如果满足终止条件，则终止迭代，否则返回Step 2。

4 仿真实验

4.1 测试函数

为了论证DCAPSO算法的有效性，我们通过五个经典的测试函数对本文的算法进行验证，并与文献[6]的随机惯性权重（RIW）、文献[7]线性递减权重（LDW）、非线性型函数权重策略（EW）、文献[11] MeanPSO算法进行实验对比，以观察它们在相同环境下性能差异。

实验环境如下：Intel（R） Core（TM） i7-10510U CPU @ 1.80GHz  2.30 GHz，RAM 16.0 GB，64位操作系统，MATLAB 2018a。五种经典的测试函数如表1所示。

4.2 实验测试和结果

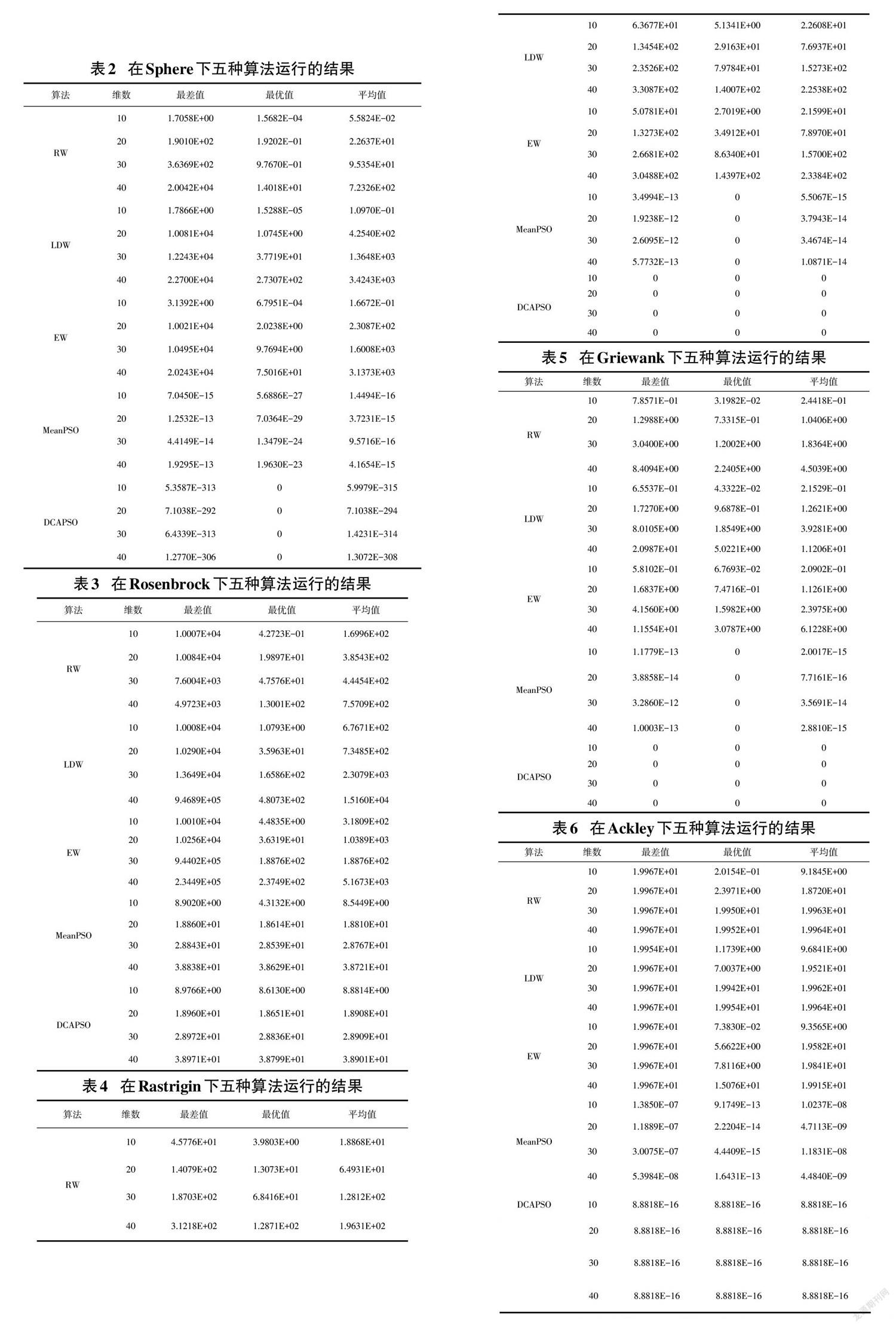
在本文的实验中，五种算法的c1和c2 均设为2;wmin取0.1，wmax取0.9;种群数取40;最大迭代次数tMax=300。对于给定的五个测试函数，每个算法各运行100次，找出在迭代过程中的最差值、最优值、平均值。五种算法的实验数据对比结果如表2～表6所示。

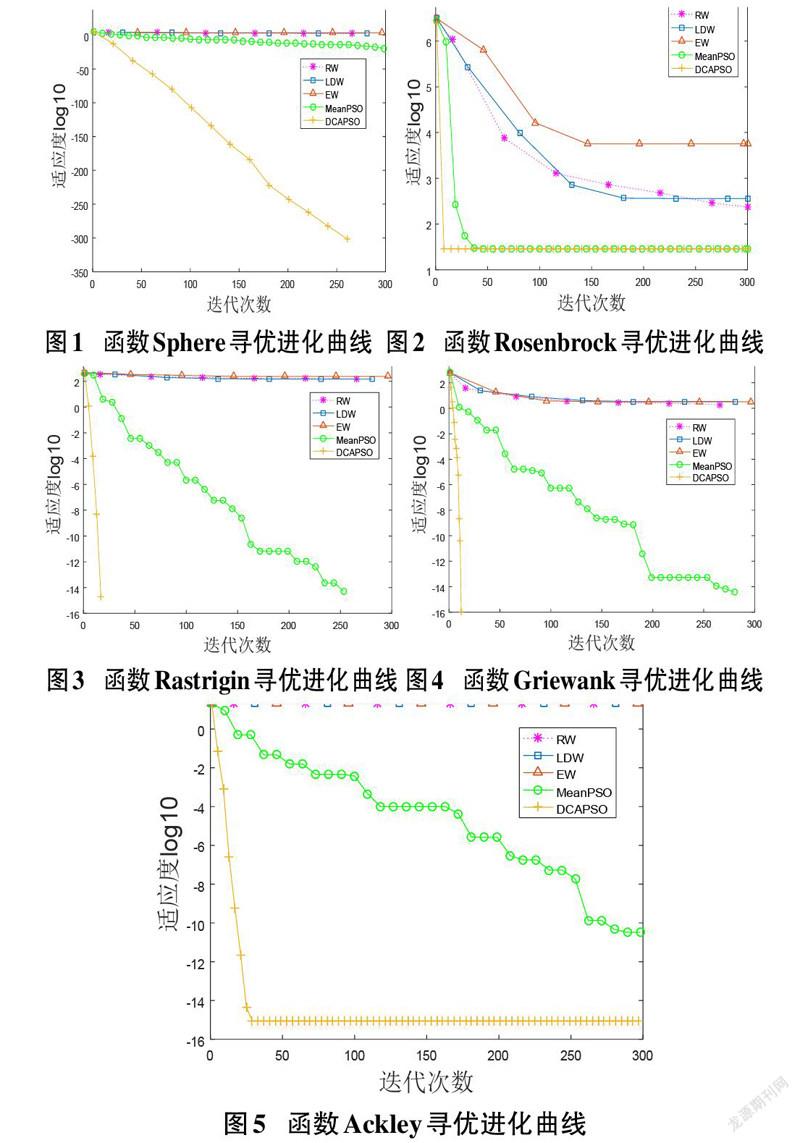
图1～图5分别为算法五种算法优化测试函数f1～f5在维数取30的寻优进化曲线，图中的横坐标表示迭代次数，纵坐标表示适应度，即每次迭代得到的全局最优值（取常用对数log10）。

从表2～表6和图1～图5可得：本文提出的DCAPSO算法在大部分性能上明显优于其他四种算法;而且在维数增加时，该算法依然比其他四种算法具有更快的收敛速度和收敛精度，鲁棒性更好。

5 结束语

本文提出了DCAPSO算法，该算法采用粒子的距离代价Fi（L，D）与两个平均距离代价F_avg1、F_avg2的差值作将种群划分为三个不同的等级，并针对等级不同的粒子采取相应的惯性权值策略来更新粒子当前的速度和位置，并在每次迭代的过程中对全局最优加入一个服从正态分布的扰动因子，加入的扰动因子既有利于增加全局最优活性，又保持了种群的多样性，同时融入了MeanPSO的思想。仿真实验使用5个基准函数对比了5种算法，对比证明了本文提出的算法，在优化性能上更有优势。具体体现在更少的迭代次数找到最优解，并且拥有更快的收敛速度以及更好的收敛精度。原因在于其在原PSO基础上加强了全局搜索能力以及后期收敛的微调能力。总而言之，本文提出的改进算法是一种兼具效果和速度的粒子群优化算法。研究标准粒子群优化算法其他参数的距离代价对算法的影响是今后的研究内容。今后进一步的研究方向将集中于把本文提出的优化算法实践于应用中，以期进一步验证算法的有效性，并发掘其实际应用价值。

参考文献：

[1] Kennedy J， Eberhart R. Particle swarm optimization[C]//IEEE International Conference on Neural Networks， 1995. Proceedings. IEEE， 2002：1942-1948.

[2] Liu Weixin，Wang Yujia，Liu Xing，et al. Weak thruster fault detection for AUV based on stochastic resonance and wavelet reconstruction[J].Journal of Central South University2016，23（11）：2883-2895.

[3] 張涛，张明辉，李清伟，等.基于粒子群-支持向量机的时间序列分类诊断模型[J].同济大学学报（自然科学版），2016，44（9）：1450-1457.

[4] 罗淑娟，白思俊，郭云涛.决策者偏好交互项目组合选择模型及算法优化研究[J].西北工业大学学报，2016，34（4）：724-730.

[5] 范成礼，付强，邢清华.基于改进PSO的临空高速飞行器协同跟踪优化[J].系统工程与电子技术，2017，39（3）：476-481.

[6] Eberhart R C， Shi Y. Tracking and optimizing dynamic systems with particle swarms[C]// Evolutionary Computation， 2001.Proceedings of the 2001 Congress on. IEEE， 2002：94-100.

[7] Shi Y， Eberhart R. A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation Proceedings， 1998. IEEE World Congress on Computational Intelligence. IEEE Xplore， 1999：69-73.

[8] Shi Y， Eberhart R C. Particle swarm optimization with fuzzy adaptive inertia weight[J].Nature， 2001， 212（5061）：511-512.

[9] 周俊，陈璟华，刘国祥，等.粒子群优化算法中惯性权重综述[J].广东电力，2013，26（7）：6-12.

[10] 杨善林，李永森，胡笑旋，等.K-MEANS算法中的K值优化问题研究[J].系统工程理论与实践，2006，26（2）：97-101.

[11] Deep K，Bansal J C.Mean particle swarm optimisation for function optimisation[J].International Journal of Computational Intelligence Studies，2009，1（1）：72.

【通联编辑：代影】

收稿日期：2021-12-24

基金项目：教育新一代信息技术创新项目（2020ITA03027）;广西2020年度中青年教师基础能力提升项目（2020KY41016）;广西农业科技自筹经费项目（Z2019102）;广西农业职业技术大学2021年科学研究与技术开发计划课题（YKJ2124）

作者简介：黄欣（1983—），男，广西平南人，副教授，硕士研究生，主要研究方向为计算机网络技术;丘刚玮（1985—），男，广西贺州人，工程师，学士，主要研究方向为计算机技术;唐伟萍（1983—），女，广西玉林人，通信作者，副教授，学士，主要研究方向为计算机技术应用。