水下爆破激励堤岸振动主频的衰减规律❋
2022-04-08付艳恕王海涛
李 飞 付艳恕 顾 云 王海涛 唐 毅
①核工业南京建设集团有限公司(江苏南京,211102)
②南昌大学机电工程学院(江西南昌,330031)
引言
众多资料分析表明,随着传播距离的增加,爆破振动波振动主频(介质质点最大振幅所对应波的频率)会不断降低,高频成分振动波衰减速度更快,而低频成分振动波衰减相对较慢。因此,在距离爆源较远处,爆破振动波的低频成分起主要作用。而低频率更接近建(构)筑物的固有频率,从而引起结构共振的可能性更大,对建(构)筑物造成振动破坏。
振动主频是爆破振动危害三要素之一[1]。《爆破安全规程》(GB6722—2014)[2]给出建(构)筑物爆破振动安全的判据时,也考虑了爆破振动主频的影响。
目前,国内外关于爆破振动主频随传播过程衰减规律的研究包括基于爆破振动强度影响因素提出经验公式[3],或基于实验测试给出计算建议[4],或基于波的传播理论导出均匀介质中主频衰减规律[5]。事实上,爆破振动波传播行为与介质属性紧密关联,通常采用量纲分析寻找物理现象之间的规律[6-7]。以上研究都是基于露天爆破,并没有考虑水域因素。
相比于岩土爆破,水下爆破对堤岸近邻域结构的振动激励存在两个显著的差异:一是因流体状态的水介质不能承受剪切载荷而无法传递横波,使得水下爆破对堤岸近邻域结构振动激励天然地过滤掉了横波成分,而主要呈现为纵波激励;二是因水介质与岩土介质波阻抗的差异,使得来自于水下爆破的纵波在水、土界面上发生入射、反射和透射,具体的入射波、反射波、透射波强度与水、岩土介质波阻抗相关。因而,为了评价水下爆破振动对堤岸及其近邻域建筑结构的影响,有必要了解爆破振动主频传播过程中随介质变化的衰减规律。
本文中,结合桥梁爆破拆除项目,考虑水下爆破振动在堤岸及其近邻域传播所伴随的水、土介质变化特征,运用量纲分析推导出水下爆破振动主频的泛函关系式;然后,采用回归拟合方法求解出具体的爆破振动主频预测公式;最后,将预测结果与实测结果进行对比,验证所得水下爆破振动在堤岸近邻域传播主频预测公式的合理性。
1 振动波界面传播行为
当振动波从一种介质进入到另一种介质时,会在两个介质的分界面处发生反射及透射。假设振动波在介质I和介质II中传播,ρ、c分别为介质密度和体波声速,相应的波阻抗分别为ρ1c1和ρ2c2。在分界面附近,两种介质由于波动扰动得到的法向速度分别为v1和v2,得到的压力分别为p1和p2。
如图1所示,根据介质分界面处的波动边界条件,两种介质的压力在分界面处连续,法向速度相等。即

图1 振动波在两种介质传播的分界面Fig.1 Interface of vibration wave propagation in two media

对于振动波斜入射,当振动波传播方向在xy平面内,入射于分界面上时,与x轴的夹角为θr;反射与透射时,与x轴的夹角分别为θf和θt,见图2。

图2 波动斜入射时的反射和透射Fig.2 Reflection and transmission of vibration wave at oblique incidence
通过对振动波斜入射时计算入射、反射及透射时压力与速度的连续条件,计算入射波、反射波及透射波的压力与速度公式,见表1。

表1 声波斜入射时入射波、反射波及透射波的压力与速度公式Tab.1 Pressure formulas and velocity formulas of incidence wave,reflection wave and transmission wave of sound wave at oblique incidence
振动波斜入射时,根据连续性边界条件,入射、反射及透射时,在x=0的分界面处,扰动压力与质点速度有:

式中:pr为入射波压力;pf为反射波压力;pt为透射波压力;vrx为入射波质点速度;vfx为反射波质点速度;vtx为透射波质点速度。
再根据斯奈尔声波反射与折射定理[8],有

本文中,式(4)中的vtx实际上是爆破振动强度的判据。从式(4)可以看出,波动在分界面上的vtx由入射波的质点速度、波阻抗、入射夹角以及透射夹角共同决定。也即由于界面的存在,使得入射角与透射角对应的几何参数(图3)影响着爆破振动波的强度,从而影响着爆破振动主频。
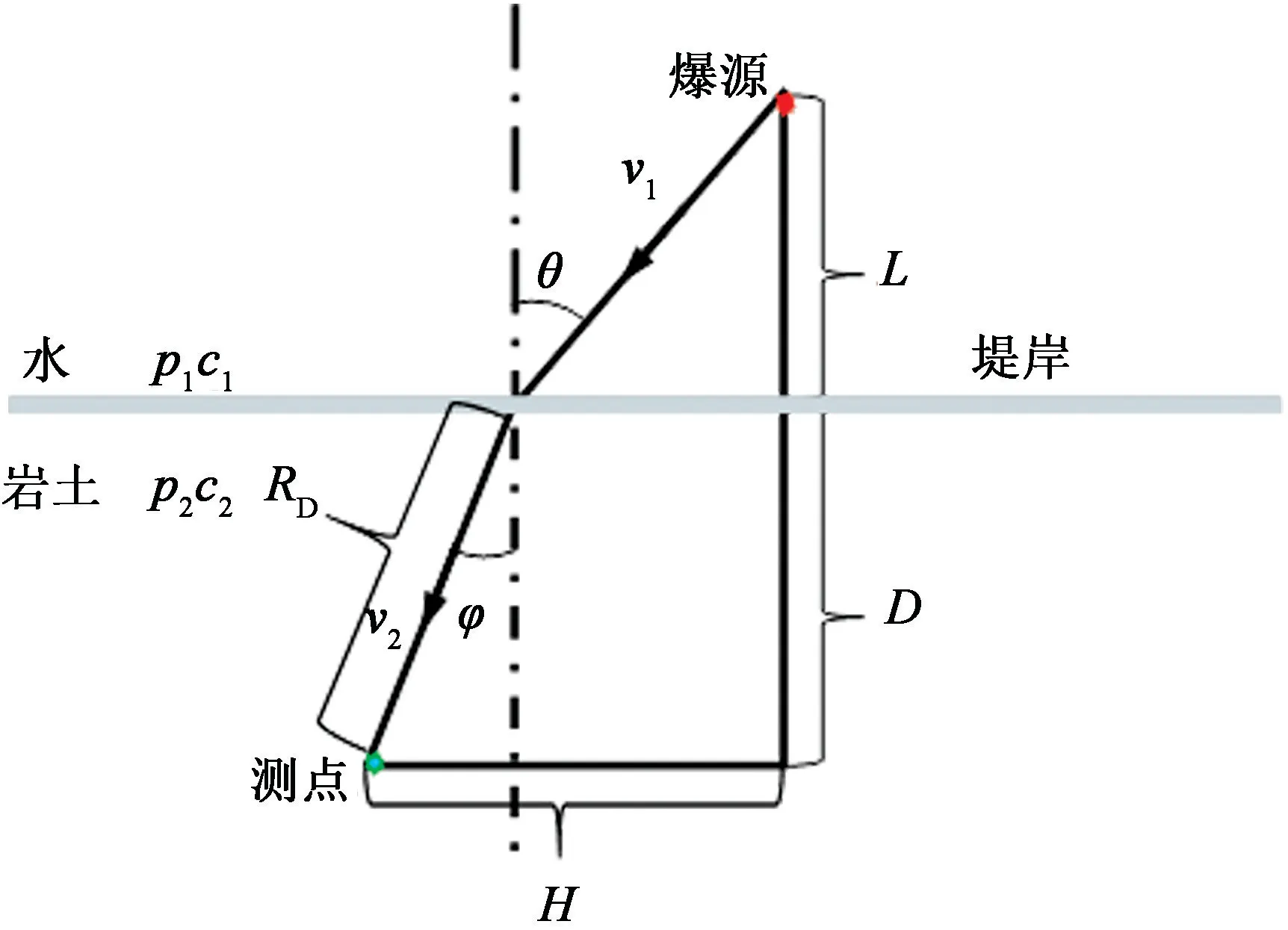
图3 振动波从水斜入射到岩土Fig.3 Oblique incidence of vibration wave from water to rock and soil
2 水土耦合域振动传播主频泛函
研究水下爆破振动在堤岸及近邻域传播(图3)时,由几何关系可知:
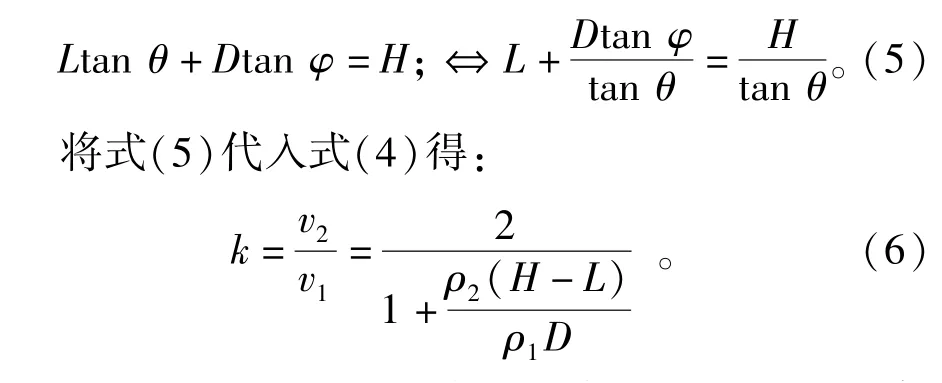
从式(6)可以看出,波动在介质界面上的透射由两介质密度与空间几何参数H、L、D共同决定。
然而,由于介质物理属性的变化,水下爆破振动在水、土介质中的传播距离和入射角度等因素各异,使得爆破振动传播规律较为复杂,建立明确的物理、数学方程极为困难,此时便需要采用量纲分析法[9]建立相应的经验公式,推导振动主频衰减规律。
影响爆破振动主频的自变量[10-13]分别是炸药量Q、爆心距R、测点到堤岸的距离RD、介质密度ρ和介质中纵波传播速度cp。爆破振动主频f作为因变量,根据∏定理得到以下函数式:

由式(7)知,物理量个数为n=6。根据∏定理,取基本量为Q,R,cp,故基本量的量纲数为m=3,导出量与因变量的量纲数为n-m=3,∏、∏1、∏2代表的是无量纲变量,则有:

式中:α、β、γ均为待定系数。
以T、M、L分别表示时间、质量及长度的量纲,则各物理量的量纲如表2所示。

表2 水下爆破振动的物理量及量纲Tab.2 Physical parameters and dimensions in underwater blasting vibration

对式(9)等号两边对应量纲指数进行求解,可得:α=0,β=-1,γ=1;α1=1,β1=-3,γ1=0;α2=0,β2=1,γ2=0。

由上述计算可得无量纲变量之间的函数关系式为:

式中:K是场地系数;β1是衰减系数;β2是与水陆距离相关的影响系数。
3 振动主频函数回归拟合
在式(14)中:Q、R、RD是已知量;K、β1、β2是待定参数,即需要根据测试所得振动数据进行拟合求解的参数。
在数学上,解决这类问题通常采用非线性最小二乘法[14-15]。
用非线性最小二乘法求待定参数K、β1、β2,使目标函数最小。

式中:w=[K,β1,β2]T是待定参数。
目标函数f(w)取最小值的必要条件为:
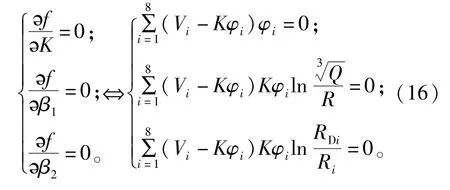
式(16)是一个非线性方程组,一般采用数值迭代法进行求解。采用高斯-牛顿迭代法求解[16],获得非线性方程组近似解K、β1、β2,从而求出式(14)。对于式(14)中待定参数拟合效果,可以根据残差平方和Rss来测定:

4 基于实测数据导出主频函数
4.1 振动测试结果
宜春秀江双桥位于在江西省宜春市袁州区城西的秀江河之上,于1951年建成,至1984年加建一座桥梁。桥长193 m,为双幅桥,由主桥和辅桥组成。由于规划建设需要,需将双桥爆破拆除。经现场勘察,双桥连接宜春南路和宜春北路,东西方向为秀江下游和上游,南北两侧为闹市区,周围环境较复杂。其中,在北侧最近处建筑物有东面55 m处的培训楼和西面35 m的超市;南侧最近处建筑物有54 m处的职业学校;西面200 m处有第二附属医院。受保护建(构)筑物众多,爆破振动备受关注。利用NUBOX-6016爆破测振仪对项目水下爆破激励下堤岸振动进行监测,测点布置方案如图4所示。新、旧两幅桥延时爆破,4个测点(图4中★号)共得到8组数据,测点离爆心空间距离见表3。

表3 爆破振动监测数据 Tab.3 Monitoring data of blasting vibration
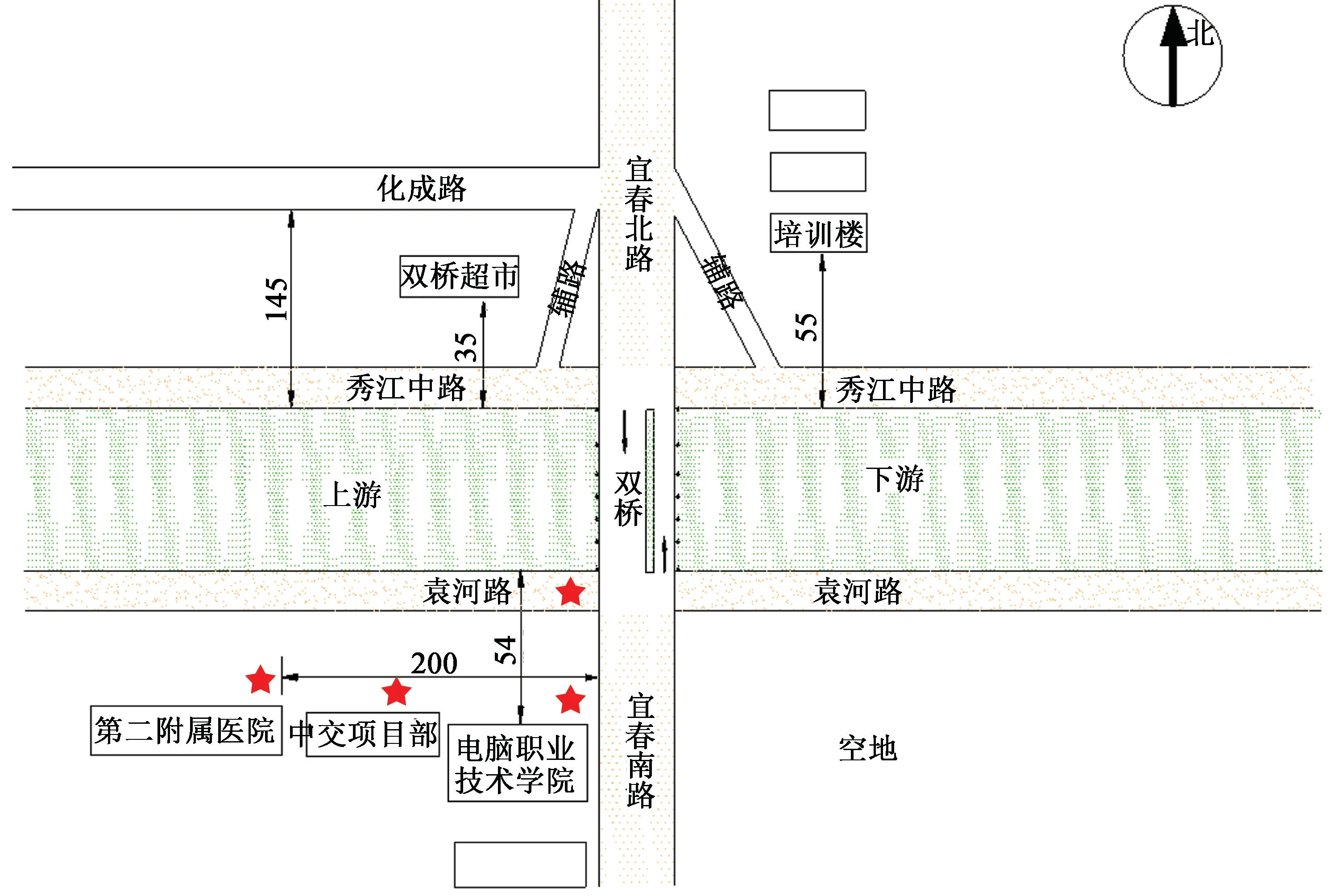
图4 测点布置(单位:m)Fig.4 Layout of measuring points(Unit:m)
4.2 振动主频函数表达式
在采用非线性最小二乘法的基础上,用Matlab编写的程序对式(14)和式(18)分别进行拟合求解,得到表4所示结果。
根据表4可以看出,采用量纲分析推导出的式(14)的残差平方和更小,故拟合效果更优。
那么根据表4列出的参数,可知式(18)和式(14)的具体表达式分别为:

表4 拟合参数Tab.4 Fitting parameters
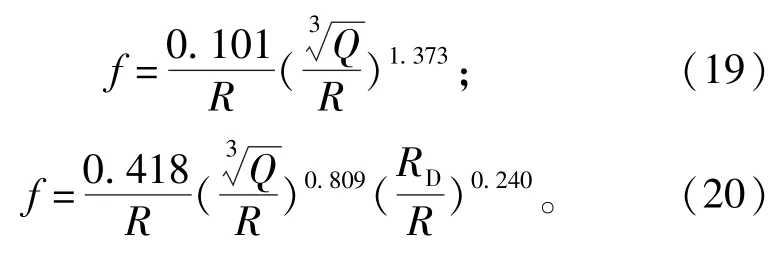
由式(19)、式(20)可以分别计算对应的爆破振动主频预测值,具体结果见表5。
由表5可以看出,采用式(18)计算出的平均相对误差为27.29%,而采用(14)计算出的平均相对误差为8.87%。采用量纲分析推导出的式(14)拟合的振动主频能够较准确地反映水土耦合作用下的爆破振动,预测的水下爆破振动在堤岸近邻域传播主频与实验测试结果相关性更优,体现了本研究方法的合理性。

表5 爆破振动主频的实测与预测结果Tab.5 Measured and predicted results of dominant frequency of blasting vibration
5 结论
基于江西省宜春市秀江双桥水下墩台爆破拆除项目测试数据,考虑水、土介质变化特征,采用量纲分析法导出了水下爆破激励下堤岸振动主频衰减规律表达式,并与未考虑水、土介质变化特征的预测方法进行对比,得出以下结论:
1)通过综合影响系数呈现水、土介质物征变化对振动传播主频的影响,同时引入监测点距爆心之间水、土介质传播域距离比值系数,使得振动主频预测表达式在物理上尊重水下爆破振动在堤岸传播工程实际,所得结果更具科学、合理性。
2)通过比较回归拟合中的残差平方和可知,较之于未考虑水、土介质变化预测方法而言,基于量纲分析推导出的公式对于爆破振动主频预测的精度较高,能够更好地反映水下爆破振动主频衰减规律。
3)通过预测与实测爆破振动主频的相对误差,可以看出本文研究方法得到的振动主频预测值能够较准确地反映水下爆破在堤岸近邻域振动主频的衰减规律。
