基于KPCA-WOA-ELM的爆破飞石距离预测❋

陈 资 李 昌

广东理工学院工业自动化系(广东肇庆，526100)

引言

爆破飞石是由爆炸能量突然引起的抛掷泥土和岩石碎片[1]。飞散到爆破安全区以外的飞石容易造成爆破周边地区工作人员伤亡、建(构)筑物以及机械设备损坏[2]。根据调查统计，20%～40%的爆破相关事故是由飞石引起的[3]。因而，在工程爆破前实现对爆破飞石距离的精准预测、确定合理的爆破安全区域显得十分重要。

爆破飞石距离受到岩石性质、爆破设计参数、炸药参数等众多因素影响[4]。而基于传统经验公式法预测爆破飞石距离方法考虑的影响因素少，且无法描述各个因素之间复杂的、不确定性的非线性关系，所以预测准确性不高[5]。鉴于此，一些学者以机器语言算法为基础理论预测飞石距离，包括BP神经网络[6]、Elman神经网络[7]、深度神经网络(DNN)[8]、粒子群算法优化的人工神经网络(PSOANN)[9]、支持向量回归和灰狼算法组合算法(SVRGWO)[10]等。以上方法对爆破飞石距离的预测取得了一定成果，但是大部分方法采用过多关联因素进行分析，增加了预测模型的复杂度和冗余度，降低了预测效率和准确性。

综上所述，针对影响因素间存在非线性关系的特征，利用核主成分分析(kernel principal component analysis，KPCA)方法筛选出包含主要信息的主成分作为预测模型输入变量，并通过全局搜索能力强的鲸鱼算法(whale optimization algorithm，WOA)对极限学习机(extreme learning machine，ELM)的主要参数进行优化，克服ELM易陷入局部最优解的缺点，最终建立KPCA-WOA-ELM爆破飞石预测模型，为爆破安全防护工作提供新方法。

1 基础理论

1.1 核主成分分析(KPCA)法

KPCA是一种在主成分分析法基础上改进的线性主元分析方法。其基本思想是将低维样本数据通过核函数非线性映射到高维空间，然后对样本数据在高维度进行线性降维[11]。KPCA能在不丢失原始样本信息的基础上最大限度处理非线性数据，在非线性样本数据特征提取问题上得到广泛应用[12-13]。KPCA原理和具体步骤参见文献[14]。

1.2 鲸鱼算法(WOA)

WOA是一种新型的启发式搜索优化算法。其主要思路是模拟鲸鱼包围猎物、猎杀猎物、搜索猎物等一系列狩猎行为，最终获得猎物的坐标位置，即最优解[15]。

在捕食行为中，鲸鱼会通过收缩包围猎物，其不断迭代过程可以通过以下数学模型描述:

式中:D为鲸鱼与猎物间的向量距离；X和Xp分别表示鲸鱼和猎物的位置向量；t为当前的迭代次数；r为随机向量；A为系数向量，用于判断算法离最优解的距离；C是包含[0，2]随机值系数的向量，用于增加狩猎过程随机性，避免算法得到局部最优解；a为收敛因子；tmax为最大迭代次数。

另外，依据猎物所处的位置使用螺旋方程来更新鲸鱼的位置:

式中:D′为捕食时的鲸鱼与猎物间的向量距离；b为螺旋形状的常数；l为[-1，1]之间的随机数。

鲸鱼在捕食过程中会同时通过收缩包围猎物和螺旋形状绕着猎物游动，鲸鱼位置通过以上2种方法的50%概率来获取:

1.3 极限学习机(ELM)

ELM是在单隐层前馈神经网络基础上改进的新型智能学习算法，ELM设置参数少、学习速度快、泛化能力好、对非线性样本数据具有较好适用性，被广泛应用于各种预测、分类和回归问题。

对于输入层神经元个数为n、隐含层的节点个数为L、输出层神经元个数为m的ELM结构网络，给定训练样本(xj，tj)、输入向量xj＝[xj1，xj2，…，xjn]T、期望输出向量tj＝[tj1，tj2，…，tjm]T，其中，j＝1，2，…，N。则期望输出值为:

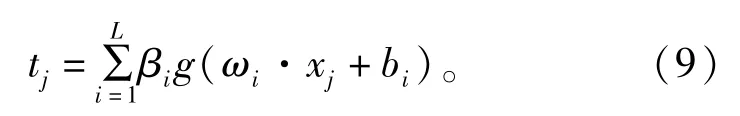
式中:ωi为输入权值矩阵；bi为隐含层神经元阈值；βi为输出权值；g(x)为激活函数。

将式(9)转换成行列式形式:

式中:H为隐含层的输出矩阵；T为目标期望输出矩阵。

输出权值矩阵β为:

式中:H+为矩阵H的Moore-Penrose广义逆矩阵。

2 KPCA-WOA-ELM模型的建立

为提高爆破飞石预测结果的精度和效率，消除爆破飞石距离影响因素之间的非线性、强耦合和高冗余，解决ELM参数选择不足等问题，建立爆破飞石距离KPCA-WOA-ELM预测模型，具体流程如图1所示。

图1 KPCA-WOA-ELM模型流程图Fig.1 Flow chart of KPCA-WOA-ELM model

为了验证KPCA-WOA-ELM模型的预测性能，引入均方根误差RMSE、决定系数R2以及平均绝对误差RMAE作为模型评价指标，计算公式如下:

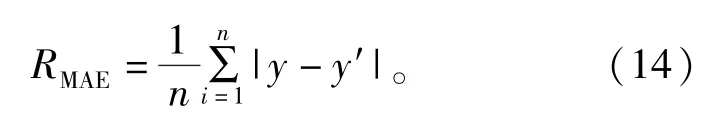
式中:y、y′、¯y分别是爆破飞石距离真实值、预测值和真实值的平均值。

3 实例分析

3.1 因素分析与数据获取

爆破飞石距离Df与许多方面因素有关，如爆破参数、装药工艺、岩石性质等。合理选取影响因素是确保预测有效性的前提。通过参考国内外相关的文献以及咨询相关矿业专家和现场施工人员的具体意见，选取炮孔直径dB、炮孔深度hD、堵塞长度L、炮孔排距与孔距比B/S、最大段药量mC、炸药单耗Q和岩石质量指标RQD7个主要影响因素对爆破飞石距离进行研究。选取某露天矿的40组监测数据作为原始样本集，如表1所示。

表1 原始样本参数Tab.1 Data of original samples

3.2 KPCA降维

利用KPCA对原始数据样本集进行核主成分提取，各核主成分累计贡献率和特征值如图2所示。由图2可知，前4个主成分的累计贡献率已经达到95.76%，故提取前4个核主成分F1、F2、F3和F4代替原来的7个影响因素，降维后的样本数据如表2所示。

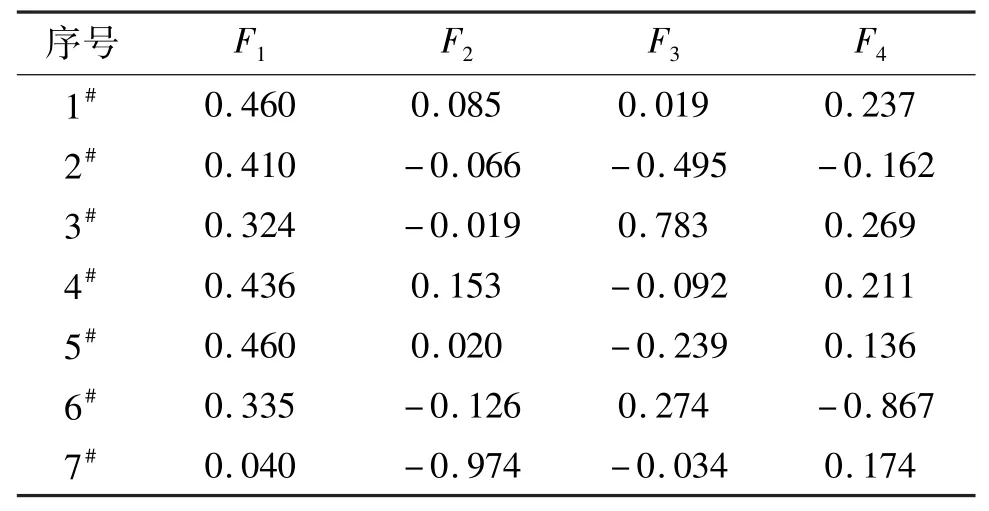
表2 降维后的样本数据Tab.2 Sample data after dimensionality reduction

图2 各核主成分累计贡献率和特征值Fig.2 Cumulative contribution rate and eigenvalues of each nuclear principal component

3.3 模型训练及结果分析

将得到的4个主成分作为预测模型输入变量，以爆破飞石距离为输出变量，并选取KPCA重构后的数据中前80%作为预测模型的训练样本，剩余20%作为测试样本。

模型中相关参数设定:ELM模型中隐含层激励函数为Sigmoid函数，输入层神经元个数为1，隐含层的节点个数为6，输出层神经元个数为1；WOA算法中，鲸鱼种群规模为30，最大迭代次数为200。

为验证KPCA-WOA-ELM模型在爆破飞石距离预测中的可靠性和有效性，对原始样本数据分别建立WOA-ELM和PSO-ELM模型，并对3种模型预测结果进行分析。3种模型预测的迭代过程、预测结果以及相对误差对比分别如图3、表3和图4所示。 由图3可知，相较于使用PSO-ELM，使用WOAELM收敛速度更快，并且经过KPCA降维，同样也能提高收敛效率。由表3可知，KPCA-WOA-ELM、WOA-ELM和PSO-ELM模型的平均相对误差分别为4.271%、5.998%和8.997%，说明在相同的条件下，KPCA-WOA-ELM模型预测精度更高。并且由图4可知，KPCA-WOA-ELM模型相对误差曲线的波动最小，证明了该模型预测结果稳定性更强。

表3 飞石距离预测结果Tab.3 Prediction results of flyrock distance

图3 不同模型的迭代过程曲线Fig.3 Iteration process curves of different models

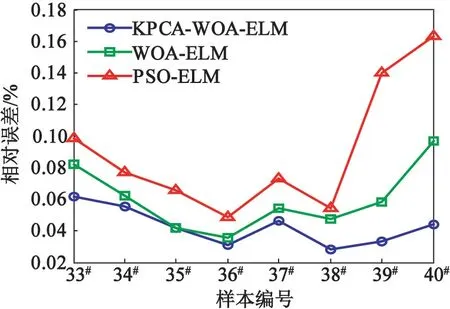
图4 不同模型相对误差对比Fig.4 Comparison of relative errors of different models

为了深入比较3种模型预测效果，采用均方根误差、决定系数以及平均绝对误差作为评判指标，结果如表4所示。分析表4可知:KPCA-WOA-ELM模型的RMSE和RMAE分别为6.681和6.413，显著优于其他模型；另外，该预测模型的R2为0.985，比WOA-ELM模型的和PSO-ELM的R2更接近于1，反映出KPCA-WOA-ELM模型拟合度更高，预测精度更好。

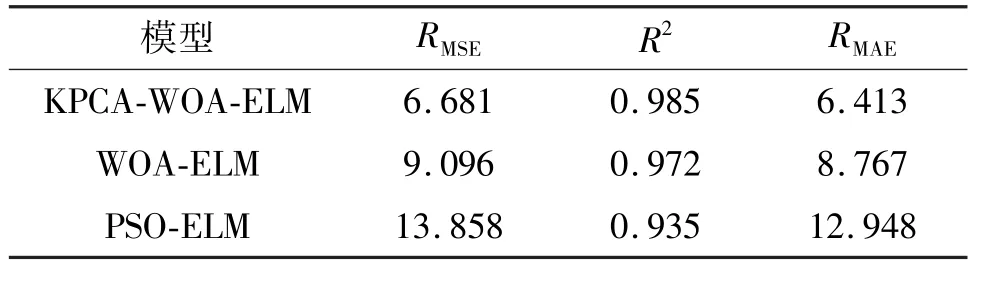
表4 模型评价指标结果对比Tab.4 Comparison of model evaluation index results

综上分析可知:在KPCA-WOA-ELM模型中，KPCA能在保留原有信息的前提下，降低影响因素之间信息的重叠；并且WOA算法能够克服ELM易陷入局部最优解的问题，提高模型预测精度和效率，使得预测值更贴近于真实值。

4 结论

1)选取影响爆破飞石距离的7个主要因素，在不遗失原始样本信息的前提下，通过KPCA筛选出包含主要信息的4个主成分，降低了样本数据间的耦合性和冗杂性，有效提高模型的预测效率和精度。

2)使用WOA算法对ELM参数进行寻优，解决了传统ELM参数人工选择具有盲目性、收敛速度慢、容易陷入局部最优等问题，强化了模型学习能力和泛化能力。

3)应用实例结果表明，KPCA-WOA-ELM预测模型的各项评价指标均优于WOA-ELM和PSOELM模型。该模型的提出为爆破飞石距离预测提供了一种更为可行的新思路。