素养立意下解析几何专题复习常规与转向

【摘 要】 素养立意下的解析几何专题复习，在高考导向、总结归纳、突出常规的同时要转向注重知识间的融合，注重培养学生问题解决能力;要转向落实细节，注重回归教材的方式方法，培养惯性观念时注重学生运算难点的突破，运用变式教学提升学生核心素养;要转向高考试题命题技术、共性联系、创新研究等方面的总结和预测上来，从而把握命题方向.

【关键词】 素养立意;解析几何;变式教学;命题技术;共性联系

高考评价体系标志着中国高考正在实现从能力立意到素养导向的历史性转变.回顾2021年素养立意下的解析几何考题，可总结为：强化“四基”、考查“四能”;主要表现在突出主干知识，重视解析几何的本质、基本思想与方法，考查学生直观想象、逻辑推理、数学运算等核心素养以及分析问题、解决问题的能力.因此，作为素养立意下的专题复习，注重常规的同时，还必须适时“转向”，跳出“刷题”模式，笔者认为可以从以下方面把握与提升.

1 高考导向，总结归纳1.1 突出常规情境，注重基本思想与技能

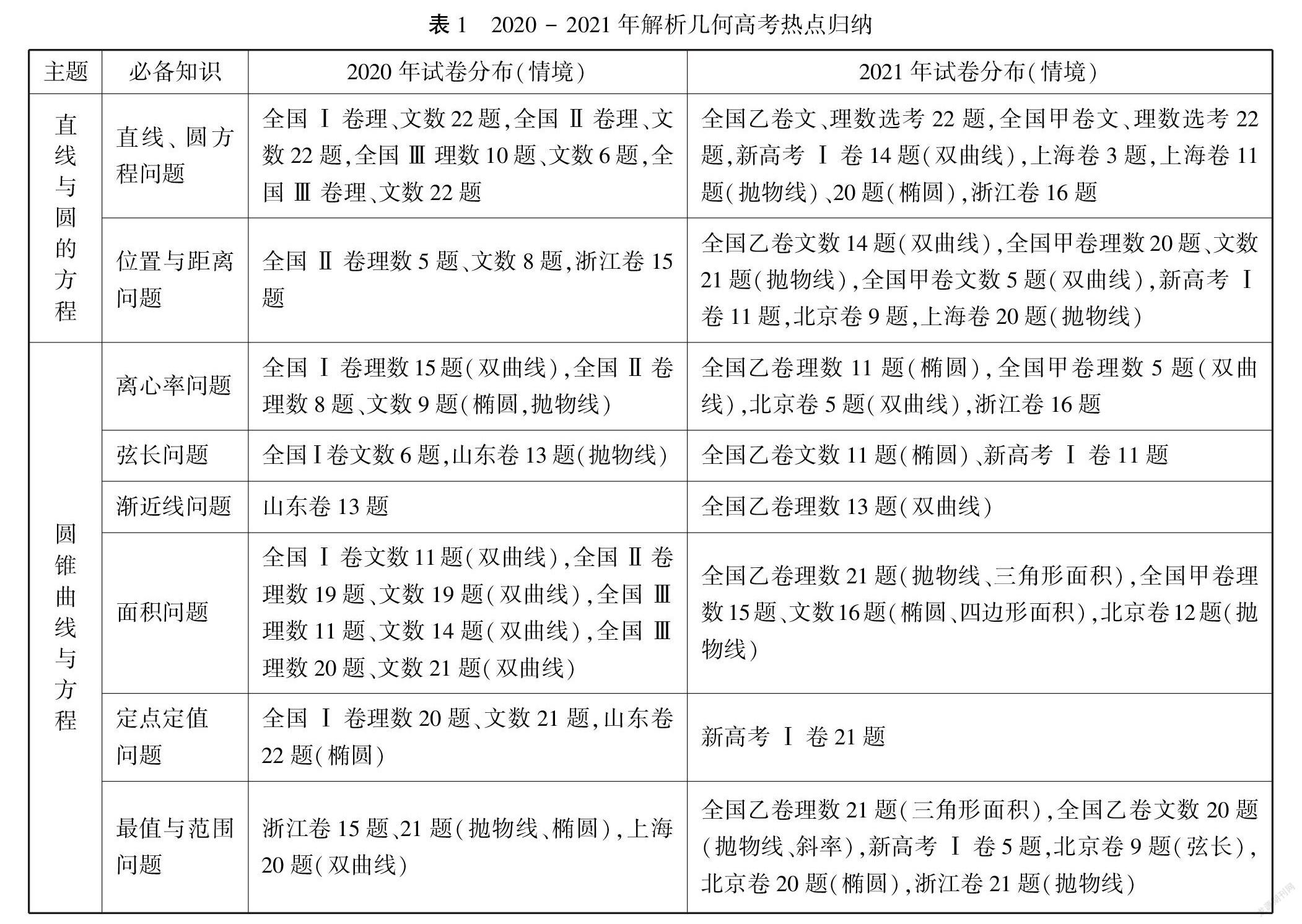
《普通高中课程标准（2017年版2020年修订）》[1]（以下简称课标）指出，平面解析几何内容包括：直线与方程、圆与方程、圆锥曲线与方程、平面解析几何的形成与发展.课标对每部分的考查要求作了明确，但高考中直线、圆的方程很多时候融入圆锥曲线与方程的知识当中进行综合考查，因此，圆锥曲线与方程是解析几何的核心内容.梳理近两年的解析几何考查热点，大致可归纳如下：

从表1不难发现，高考试题主要以变换曲线类型、几何性質和位置关系为载体，基本上在距离问题、面积问题、最值与范围问题、定点定值问题等典型问题情境上做文章.

1.2 体现知识融合，注重问题解决能力

除了常规的考查方式，素养立意下的高考试题要素已经从单一要素转向复合要素，这导致更注重考查知识的融合;同时随着不定项多选题的出现，对解析几何专题的要求更强调知识的迁移和问题解决能力.

1.2.1 考查多选题与解析几何知识的融合

例1 （2020年山东卷9题）已知曲线C：mx2+ny2=1.

A.若m>n>0，则C是椭圆，其焦点在y轴上

B.若m=n>0，则C是圆，其半径为n

C.若mn<0，则C是双曲线，其渐近线方程为y=±-mnx

D.若m=0，n>0，则C是两条直线

评析 此题以圆锥曲线统一形式为情境载体，根据参数的变化，融合了不同曲线类型的知识，要求考生能从基础知识出发，进行具体问题具体分析，在分类讨论的基础上进行逻辑推理，最后落脚在曲线（直线）方程、渐近线等常规问题的解决上.值得一提的是，解析几何的多项选择题紧接着出现在2021年新高考Ⅰ卷11题，以直线与圆的方程为载体，落脚在动态变化和对距离的考查上.1.2.2 考查解析几何与函数知识的融合

例2 （2020年浙江卷8）已知点O（0，0），A（–2，0），B（2，0）.设点P满足|PA|–|PB|=2，且P为函数y=34-x2图象上的点，则|OP|=（  ）.

A.222  B. 4105  C. 7  D. 10

评析 本题体现了双曲线和函数图象的融合，同时函数图象也是椭圆的上半部分，从而也是双曲线和椭圆知识的融合.要求学生能从双曲线的定义出发，得出双曲线右支的方程，结合函数解析式得出P点坐标.考查了学生数学运算和直观想象的核心素养.值得注意的是，在2021年浙江卷第9题出现了与数列（等比数列）知识的融合.1.2.3 考查解析几何与平面向量的融合

平面向量在新人教A版教材中的位置发生了重要变化，它作为一种解决问题的工具更加受到重视.因此解析几何与平面向量的融合也就变得十分自然.比如2020年江苏卷、天津卷、上海卷中的解析几何解答题，2021年上海卷20题等.这类融合主要涉及圆锥曲线的相关知识和平面向量知识等，多出现在解答题，考查学生从代数角度寻找关于长度或者利用向量的坐标反映向量的位置关系方面解决问题的能力.2 备考转向，落实细节复习备考策略一直是一个老生常谈的问题，往往各种宏观上的指导颇多，而在复习中微观上的实际操作却比较少.下面就几点落实关键细节上的经验和想法给出建议.2.1 回归教材，注重方式方法

回归教材绝对不是在复习中简单地让学生“看看教材，做做习题”.复习备考回归教材是连续性的过程，是进入复习教学时就要思考的整体性的、全局性的计划部署，要定位如何通过对高考题和教材习题的比较、研究，达到回归教材、活用教材以及类比拓展的目的[2].

首先建立高考试题与教材的对接点.从高考试题的显性要素和隐性要素两方面建立高考试题与教材的对接点.比如，2021年全国新高考Ⅱ卷第13题可对接新人教A版选择性必修2习题3.2第3题;全国甲卷理科第15题可对接选择性必修2复习参考题3第7题等.其次，以高考为导向挖掘教材资源.根据建立的高考与教材的对接点，从高考考查的重点、高考试题的命题思路反思教材相关重点内容的问题提出方式，创新教材习题形式.最后，将对接点要融入解析几何专题中的思维导图，形成概念与概念之间的逻辑关系，以便应对知识融合时的思维跨越.2.2 培养惯性观念，突破运算难点素养立意的高考命题重视学科观念、规律的考查，考查学生扎实的学科基础，引导他们去形成思维中的惯性观念，并且能够合理的进行转化[3].思维上的惯性观念往往在解析几何解答题中体现为：需要联立直线与曲线方程，利用韦达定理整体代换进行求解，所得表达式有时候可以很快求解，有时候就需要一些技巧，这时学生就容易卡壳.这是学生运算的难点，因为这里涉及到两种运算结构.2.2.1 对称结构

转化表达式中只含“x1+x2”（或“y1+y2”）、“x1x2”（或“y1y2”）的结构，我们俗称其为“对称结构”.例3 （2021年新高考Ⅰ卷21题）在平面直角坐标系xOy中，已知点F1（-17，0），F2（17，0），点M满足|MF1|-|MF2|=2，记M的轨迹为C.

（1）求C的方程;

（2）设T点在直线x=12上，过T的两条直线分别交C于A，B两点和P，Q两点，且|TA||TB|=|TP||TQ|，求直线AB的斜率与直线PQ的斜率之和.

评析 第（2）问中可用弦长公式转化为|TA||TB|=1+k2AB·|xA-12|·1+k2AB·|xB-12|=（1+k2AB）（xAxB-xA+xB2+14）.此时能直接利用韦达定理整体代换求解.再比如2021年新高考Ⅱ卷20题也是如此.2.2.2 非对称结构例4 （2020年全国Ⅰ卷理科21题）已知A，B分别为椭圆E：x2a2+y2=1（a>1）的左、右顶点，G为E的上顶点，AG·GB=8.P为直线x=6上的动点，PA与E的另一交点为C，PB与E的另一交点为D.

（1）求E的方程;

（2）证明：直线CD过定点.

评析 解答此题大部分学生的惯性思路为：由A（-3，0），B（3，0），设C（x1，y1），D（x2，y2），直线AC与BD的方程为y=y1x1+3（x+3），y=y2x2-3（x-3）根据AC与BD相交，则可得3y1x1+3=y2x2-3.此时就是非对称结构，若将CD直线方程（斜率存在时）y=kx+b代入椭圆方程得到表达式（9k2+1）x2+18kbx+9b2-9=0，由韦达定理并不能解决问题[4].教师这时应该引导、帮助学生总结处理这类问题的方法（例如平方法、积转为和等）或者规避这类非对称结构的求解方法.2.3 课堂变式教学，聚焦核心素养

课堂变式教学能总结复习备考中出现的问题，能够引导学生在熟悉的情境中抽象出数学概念和规则，并以此铺展开来，在关联的情境中分析并解决数学问题，达到触类旁通的效果.例5 （2021年八省联考数学21题（1）） 双曲线C：x2a2-y2b2=1（a>0，b>0）的左顶点为A，右焦点为F，动点B在C上.当BF⊥AF时，|BF|=|AF|.求C的离心率.

此题是解答题第（1）问，以双曲线为情境，在两直线为特殊位置关系且满足|BF|=|AF|等式关系时的离心率问题，依然落脚于常规问题.为了提升学生解决问题的能力，可以针对情境进行变式、迁移：

例6 （恩施州2022届高三第一次质量监测6题） 双曲线C：x2a2-y2b2=1（a>0，b>0）的左顶点为A，右焦点为F，过点A的直线交双曲线C于另一点B，当BF⊥AF时满足|AF|>2|BF|，则双曲线离心率e的取值范围是（  ）.

A.1<e<2   B.1<e<32

C.32<e<2D.1<e<3+32

這样，就把圆锥曲线中基本量的问题迁移到了范围问题，虽然基础知识一样，但涉及到逻辑推理、数学运算等核心素养水平是不一样的.

3 研究考向，猜想预测

加强对高考试题的研究，可以在命题技术、共性联系、创新研究等方面总结解题思路、方法，便于在关联的情境中进行迁移，把握命题方向乃至预测试题.3.1 基于命题技术研究与预测

归纳解析几何题情境中的圆锥曲线性质及去情境化的平面几何性质，总结命题技术及类似案例，能深入体会解析几何命题中利用平面几何关于三角形的一些等式关系、性质或结论进行试题命制的过程.

例7 （2019年浙江卷21题）如图1，已知F（1，0）是抛物线y2=2px（p>0）的焦点，过点F的直线交抛物线于A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，点Q在点F的右侧，记△AFG，△CQG的面积分别为S1，S2.

（1）求p的值及抛物线的准线方程;

（2）求S1S2的最小值及此时G点坐标.

若去掉抛物线的情境，可表述为：如图2，过△ABC的重心G作一条直线分别交AB，AC于F，Q，记△AFG，△CQG的面积分别为S1，S2，则S1S2的最小值为1+32[5].

结论很容易证明，也是三角形中的一条性质.有意思的是，2021年浙江卷依然是类似的命题手法.

例8 （2021年浙江卷21题）如图3，已知F是抛物线y2=2px（p>0）的焦点，M是抛物线的准线与x轴的交点，且|MF|=2.（1）求抛物线的方程;

（2）设过点F的直线交抛物线于A，B两点，斜率为2的直线l与直线MA，MB，AB，x轴依次交于点P，Q，R，N，且|RN|2=|PN|·|QN|，求直线l在x轴上截距的范围.

同样地，去掉抛物线背景，可描述为： 如图4，在MAB中，MF平分∠AMB，直线PQ与MAB的三边MA，MB，AB，MF依次交于点P，Q，R，N，如果|RN|2=|PN|·|QN|，那么BMMP·NRQN·RFFB=1. 结论的证明可利用梅涅劳斯定理，请读者自己完成.类似这样的命题手法，通过三角形性质，融入圆锥曲线的背景，应该引起关注.3.2 基于试题共性研究与预测

所谓试题共性研究，就是根据联系的多样性，对各地高考试卷解析几何的命题立意、情境设问、解法等方面进行共性研究，归纳与分类，寻找之间的联系，把握命题方向.

例9 （2021年新高考Ⅱ卷20题）已知椭圆C的方程为x2a2+y2b2=1（a>0，b>0），右焦点为F（2，0），且离心率为63.

（1）求椭圆C的方程;

（2）设点M，N是椭圆C上的两点，直线MN与曲线x2+y2=b2（x>0）相切.证明：M，N，F三点共线的充要条件是|MN|=3.

例9与例3两道真题的第（2）问解法中的条件式都是用弦长公式，转化为两交点坐标的对称结构.在命题立意上，两道高考真题都以圆锥曲线与圆的位置关系为背景，例3比较隐性，实质为A，B，P，Q四点共圆，即圆与双曲线相交于四点;例9显性的给出了圆与椭圆相切，最后二者都是以直线与曲线的位置关系为落脚点[6].

3.3 基于创新视角研究与预测

高考命题要防止试题题型、命题方式固化，增加试题新颖性和灵活性，促进学生融会贯通、真懂会用，引导中学数学全面教学、夯实基础、灵活学习、创新思考[7].同樣，解析几何题也应适当创新，可以将一些简单的几何关系融入情境，提出新的问题，培养思维能力.例10 （恩施州2022届高三第一次质量监测21题） 已知抛物线C：y2=2px（p>0）的顶点为A，直线y=x与抛物线C的交点（异于点A）到点A的距离为42.

（1）求C的标准方程;

（2）过点A作斜率为k（k>0）的直线l与C交于点M（异于点A），直线l关于直线y=x对称的直线l1与C交于点N（异于点A），求证：直线MN过定点.

解析 （1）抛物线的标准方程为y2=4x.

（2）证明：设M（x1，y1），N（x2，y2），将l：y=kx代入抛物线方程得k2x2-4x=0，所以x=4k2，y1=4k，设直线l1：y=k1x，同理x2=4k21，y2=4k1，因为l与直线l1：y=k1x关于直线y=x对称，由图形对称性，计算可得k1k=1. 所以x2=4k2，y2=4k，又kMN=y2-y1x2-x1=4k-4k4k2-4k2=k（k2-1）k4-1=k1+k2，所以直线MN的方程为y-4k=k1+k2x-4k2，化简有y=k1+k2（x+4），所以恒过定点（-4，0）.

评析 例10依然是常规情境中的定点定值问题，解题思路也是常规的惯性观念，但是“一条直线关于y=x对称的直线方程”是本题创新之处，在情境中融入了简单“对称”关系，学生在问题解决中出现了思维障碍、知识脱节，不会利用数形结合进行进一步的直观想象，不会用数学语言将其描述出来.

4 结束语

尽管年年岁岁“题”相似，岁岁年年“意”不同，但是近几年高考全国卷中解析几何内容一般包含2到3个选择与填空题、1个解答题，基本趋于稳定.各地也大多采用了三轮复习备考模式，本文中阐述的“三个方面”也是三轮复习阶段实施层面中应该重点关注的问题.总之，素养立意下的解析几何复习备考，教师要从关注知识转向关注学生，不应被“复习资料”牵着鼻子走，教学中应该立足学情，抓住解析几何本质，培养学生解决问题的能力，提升数学核心素养.

参考文献

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年2020年修订）[M].北京：人民教育出版社，2020.

[2] 周威.高考导向下的数学复习教材回归策略浅谈[J].数学通讯（上半月），2020（24）：4345.

[3] 任子朝.从能力立意到素养导向[J].中学数学教学参考，2018（13）：1.

[4] 涂序星.非对称结构圆锥曲线问题的求解策略——以2020年高考全国Ⅰ卷第20题为例[J].高中数学教与学， 2020（17）：1113.

[5] 周威.从面积比值的视角浅探2019年高考浙沪卷解析几何题[J].数学通讯，2019（24）：4042.

[6] 童继稀，周威.两道2021年新高考卷解析几何题的共性探讨[J].中学数学研究（华南师范大学版），2021（17）：12.

[7] 任子朝.高考命题创新[J].中学数学教学参考，2018（28）：1.

作者简介 周威（1985—），男，中学一级教师，恩施州教育科学研究院高中数学教研员，全日制研究生学历，理学硕士;主要从事高中数学教学研究与质量测评工作;主持了多项省级、州级教育规划课题;在国家级、省级数学等专业期刊上发表论文60余篇.