赤藓糖醇/碳纳米管复合相变材料热特性模拟研究

闫晓鑫，冯妍卉，邱 琳，张欣欣

1) 北京科技大学能源与环境工程学院，北京 100083 2) 北京科技大学冶金工业节能减排北京市重点实验室，北京 100083

人类社会正处于飞速发展时期，其背后离不开能源的支撑与消耗.伴随着一次能源的减少与二氧化碳排放的增加，全球能源与气候变暖状况均不容乐观.作为能源大国，我国提出“碳达峰、碳中和”的目标，在“双碳”背景下，能源结构从一次能源转向天然气和可再生能源对减少碳排放具有重要意义.目前可再生新能源发展势头强劲，然而风能、太阳能等新能源受到自然条件的制约，并且具有间歇性、不稳定的特点，因此有必要将这类新能源进行储存.相变储能技术借助相变材料在特定温度范围内物态转变进行储、释放能量，其原理简单、相变过程温度稳定，成为能源领域的研究热点.然而相变材料作为相变储能技术的主体材料，普遍具有热导率低的问题，这极大限制了能量利用效率，因此针对如何提高相变材料热导率进行了大量研究.

1991 年碳纳米管（Carbon nanotubes, CNTs）被首次发现[1]，此后纳米材料与纳米技术蓬勃发展.纳米材料相比传统材料具有优异的电导率、热导率、机械强度以及化学稳定性[2].碳纳米管作为纳米材料的代表性材料之一，其理论热导率高达6000 W·m-1·K-1[3-4]，常被用作相变材料的导热增强材料.在不同种类的石蜡中添加质量分数15%的碳纳米管可提高热导率323.2%，在散热器中表现出优异的蓄热降温作用[5].将脂肪酸与功能化的碳纳米管枝接后，不仅热导率得到了提升，经过2000次循环后仍具有良好的相变稳定性和化学稳定性[6].Cong等[7]在泡沫铜的基础上，使用碳纳米管进一步提高热导率，质量分数为5%的碳纳米管可在泡沫铜的基础上将热导率进一步提升1.82倍，达到棕桐酸热导率的32倍.与石墨纳米颗粒相比，碳纳米管作为导热增强材料表现更加优异，在相同的添加量下，含有CNT的复合材料表现出更高的热导率[8].

尽管实验中观察到碳纳米管出色的导热增强性能，但其背后的影响因素和机制仍需探索.随着计算机计算能力的飞速发展，采用计算机模拟已经成为一种重要的研究手段.Li等[9]采用分子动力学方法（Molecular dynamics simulation, MD）探究了碳纳米管与不同官能团的相变材料间的相互作用以及热运动特征.Tafrishi等[10]借助MD方法测量了石蜡及其复合材料的热性能，结果显示CNT比石墨烯更好地提升了石蜡的热导率.Yu等[11]设计了一种单壁碳纳米管与NaCl的复合材料并采用MD预测了其密度、熔点、导热系数和熔化焓等热性能，为熔盐相变材料的设计和应用提供了可能的指导.在采用MD方法预测材料热物性的研究中，计算热导率通常有两种方法：平衡态分子动力学（Equilibrium molecular dynamics, EMD）方法和非平衡态分子动力学（Non-equilibrium molecular dynamics, NEMD）方法.平衡态分子动力学方法基于Green-Kubo线性响应的涨落-耗散理论计算热导率，非平衡态分子动力学方法类似于实验方法的测量机制，在模拟单元上施加温度梯度，由于计算速度快被广泛采用[11-14].NEMD的计算方法一般可分为三种，第一种方法是分别设置两个区域作为热源与热沉，控制热源与热沉的温度，形成温度梯度，此时添加到热区的能量等于从冷区中移除的能量，并且与两个区域间传递的热通量成正比[15]；第二种方法是分别对热源和热沉施加/提取固定量的热能（满足能量守恒定律），得到两个区域间的温度梯度用于计算热导率[16]；第三种方法是反向扰动NEMD（Reverse non-equilibrium molecular dynamics, RNEMD）模拟，即Müller-Plathe[17]提出的动量交换算法，通过不同层内的原子速度交换构造热流，进而得到温度梯度.

赤藓糖醇（Erythritol）作为中低温区常用的相变材料具有熔化焓高的优点，然而其热导率仅有0.7 W·m-1·K-1[18].对于赤藓糖醇/碳基复合相变材料热物性的MD模拟研究较少，目前的研究大多以实验方法为主，缺少系统的理论研究.针对其热导率低的问题，本文提出一种赤藓糖醇/单壁碳纳米管复合相变材料，基于分子动力学模拟手段，预测了其热导率，并探究了碳纳米管长度、质量分数、分布方式等因素对复合材料热导率的影响，并且从声子振动角度对其潜在机制进行了剖析.

1 模型与模拟方法

1.1 模型构建

本文采用Materials studio软件进行建模.赤藓糖醇单晶胞结构如图1（a）所示，其晶格常数a=b= 1.281 nm，c= 0.681 nm[19]，对其进行 4 × 2 ×n扩胞操作，得到尺寸为5.124 nm × 2.562 nm × 0.681nnm的模拟体系，其中z方向扩胞倍数n依据碳纳米管的长度而定，随碳纳米管长度改变而发生变化.本文选择手性为（8-8）的单壁碳纳米管直径d=1.085 nm，为了探究碳纳米管长度对复合材料热导率的影响，分别构建了长度为3.9、5.2、5.9、7.4和8.6 nm的单壁碳纳米管，将其分别放入赤藓糖醇中，如图1（b）所示.保证体系x、y方向尺寸为5.124 nm × 2.562 nm不变，体系z方向的尺寸与碳纳米管长度相一致，此时5种模型中碳纳米管的质量分数均约为13%.为了探究碳纳米管添加量对复合材料热导率的影响，保持碳纳米管长度为8.6 nm，通过改变碳纳米管周围赤藓糖醇分子的个数改变碳纳米管的添加量.图1（b）展示了质量分数为8.88%和13.35%的两种情况.

图1 赤藓糖醇/碳纳米管复合结构模型图.（a）赤藓糖醇单晶胞结构；（b）碳纳米管质量分数分别为8.88%和13.35%的赤藓糖醇/碳纳米管复合结构模型Fig.1 Erythritol/carbon nanotube composite structure model: (a) erythritol single cell structure; (b) erythritol/carbon nanotube composite structure model with a carbon nanotube mass fraction of 8.88% and 13.35%

1.2 模拟方法

本文所有的模拟计算均在开源软件Lammps[20]平台进行，OVITO软件包[21]用于可视化处理.在分子动力学模拟中，势函数的选择关系到模拟结果的准确性.本文采用GROMOS 54A7力场[22]对赤藓糖醇进行描述，采用Tersoff势函数[23]描述单壁碳纳米管中碳原子间的相互作用，对于赤藓糖醇与碳纳米管间的相互作用则采用Lennard-Jones (L-J)势函数描述：

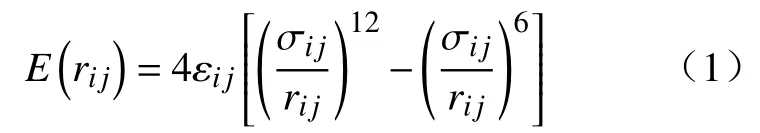
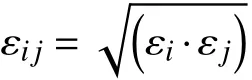
表1 赤藓糖醇与碳纳米管不同种类原子间L-J势参数Table 1 L-J potential parameters between erythritol and different kinds of carbon nanotubes

本文采用NEMD方法计算复合材料的热导率.本质上热传导是由于体系存在温度差而引起的能量传递过程，是一种非平衡过程.因此，在NEMD方法中需要构建温度梯度，等待体系达到稳态后，对体系热流以及温度梯度进行统计，根据傅里叶定律计算热导率：

1.3 模拟过程

图2为NEMD方法计算热导率示意图.在进行模拟前首先对体系进行能量最小化处理，使体系达到能量最低状态.采用Velocity Verlet算法求解运动方程，时间步长为0.5 fs，三个方向均采用周期性边界条件.模型沿热流方向均分为20层，为了防止在模拟过程中体系整体发生漂移，将z轴两端的一层原子设为固定层，分别将紧邻固定层的两层原子设置为热源与热沉.首先将体系整体置于NPT系综（等温等压系综，Constant pressure and constant temperature）下，Nosé-Hoover热浴和压浴分别用于调节系统的温度和压力.在目标温度以及1个大气压下驰豫250 ps，达到稳定状态后撤掉NPT系综.之后在NVE系综（微正则系综，Microcanonical ensemble）下分别对热源与热沉进行Langevin控温，250 ps后热源与热沉温度达到稳定状态后开始进行计算各层原子的温度，计算2 ns，取最后1 ns的数据进行统计，获得体系的温度梯度和热流，进而计算得到热导率，每个算例均进行了三次独立计算.

图2 NEMD方法计算热导率示意图Fig.2 Schematic model of the NEMD method for thermal conductivity calculation

2 结果与讨论

2.1 模型密度验证

密度是相变材料的重要热物理参数，许多研究使用密度来验证模型以及所选力场的合理性[11,27-28].我们计算了293 K温度下的赤藓糖醇在弛豫过程中的密度，结果如图3所示.在100 ps的时间内，随着弛豫时间的延长，赤藓糖醇的密度逐渐趋于稳定，因此模拟过程中设置的250 ps的弛豫时间可以使系统达到较为稳定的状态.在293 K的温度下，赤藓糖醇的密度模拟值为1422.44 kg·m-3，与文献值1440 kg·m-3[29]的误差为1.22%，这说明模型合理且所选GROMOS 54 A7力场具有较高的计算精度.

图3 293 K温度下赤藓糖醇密度随驰豫时间变化Fig.3 Density of erythritol changes with a relaxation time at 293 K

2.2 碳纳米管长度对复合相变材料热导率的影响

本文采用NEMD方法计算热导率，向热源/热沉中施加/提取的能量如图4（a）所示，满足能量守恒定律，其斜率即为热流.体系的温度分布如图4（b）所示，热源温度为310 K，热沉温度为290 K，其线性拟合的斜率即为体系的温度梯度.为了探究碳纳米管长度对赤藓糖醇/碳纳米管复合材料热导率的影响，分别计算了碳纳米管长度为3.9、5.2、5.9、7.4和8.6 nm的复合结构的热导率，结果如图5所示.随着碳纳米管轴向长度的增加，复合相变材料热导率随之提升.纯赤藓糖醇的热导率NEMD计算值为（0.67±0.04） W·m-1·K-1[28]，在本文模拟范围内，z方向（轴向）热导率达到（4.37±0.27） W·m-1·K-1（纯赤藓糖醇热导率的6.5倍），平均热导率达到（1.66±0.10 ）W·m-1·K-1（纯赤藓糖醇热导率的 2.5倍），碳纳米管的加入显著提升了热导率.碳纳米管的声子平均自由程（Phonon mean free path, MFP）与其直径成正比[30]，室温下约为500～700 nm[31-32]，由于本文模拟的碳纳米管尺寸（Lz）显著小于其声子平均自由程，此时声子以弹道输运为主，而尺寸对这种输运模式具有显著影响[33]，在弹道输运模式下，热导率几乎随几何尺寸线性增加，当几何尺寸大于声子平均自由程时，声子转为扩散热输运模式，此时热导率达到饱和值后趋于稳定[34].因而在本文模拟范围内（Lz＜ MFP），复合材料的热导率随碳纳米管轴向长度增加而显著提高.

图4 NEMD方法热流与温度分布图.（a）体系施加/提取的能量（斜率为热流）；（b）体系温度分布图Fig.4 Heat flow and temperature distribution diagram of the NEMD method: (a) energy added/subtracted by the system (the slope is heat flux); (b)temperature distribution of the system

图5 赤藓糖醇/碳纳米管复合材料热导率随碳纳米管长度变化Fig.5 Thermal conductivity of erythritol/CNT composites as a function of the length of CNT

然而，由于碳纳米管自身热导率具有较强的各向异性，使得复合材料热导率也表现出明显的各向异性.沿x、y方向（CNT径向），热导率几乎不随碳纳米管长度变化，约为0.3 W·m-1·K-1.由于碳纳米管的引入，沿x、y方向热量传递时需要经过赤藓糖醇-CNT界面，界面热阻的存在造成了能量损失，阻碍热传递，进而导致热导率降低[35]，甚至低于纯赤藓糖醇.但整体而言，赤藓糖醇/CNT复合材料平均热导率仍然呈现一定程度的提升.

2.3 碳纳米管质量分数对复合相变材料热导率的影响

碳纳米管作为导热增强材料，其添加的质量分数对复合材料热导率具有显著影响.为排除碳纳米管长度对热导率的影响，本文在保证碳纳米管长度L= 8.6 nm的前提下，仅改变碳纳米管周围赤藓糖醇分子的数量改变其添加量.如图6（a）所示，随着碳纳米管添加量增加，复合材料整体热导率得到了提升，但是依旧存在显著的各向异性.尽管碳纳米管长度相同，但是具有不同添加量的复合材料z方向热导率却随着碳纳米管质量分数增加而提高.相比于纯碳纳米管，在复合材料中赤藓糖醇与其相互作用，这会导致碳纳米管自身的热导率受影响而降低.当碳纳米管质量分数增加时，其周围的赤藓糖醇数量减少，两者间的相互作用减弱，如图6（b）所示（负值代表两者之间呈现相互吸引作用），对碳纳米管热导率的抑制减弱，进而其轴向热导率得以提升.

图6 （a）赤藓糖醇/碳纳米管复合材料热导率随碳纳米管质量分数变化；（b）赤藓糖醇与碳纳米管间相互作用能随碳纳米管质量分数变化Fig.6 (a) Thermal conductivity of erythritol/CNT composites as a function of the mass fraction of CNT; (b) interaction energy between erythritol and CNT varies with the mass fraction of CNT

2.4 碳纳米管分布方式对复合相变材料热导率的影响

当碳纳米管在相变芯材中规则排布时，热导率具有明显的各向异性，而通常实验中碳纳米管在相变芯材中随机分布，为此，本文构建了5.1 nm ×5.1 nm × 5.4 nm的模拟盒子，采用Materials Studio软件中Amorphous Cell模块以接近真实密度向盒子中随机填充赤藓糖醇分子和长度为5 nm的碳纳米管，碳纳米管个数分别为3、5、6根，模型结构如图7所示.采用NEMD方法分别计算了沿三个方向的复合材料热导率结果如表2所示，碳纳米管随机分布方式下热导率的各向异性得到了明显改善，沿各个方向的热导率均得到了提升，平均热导率随碳纳米管个数增加而升高，但增加趋势变缓.

表2 随机分布方式下赤藓糖醇/碳纳米管复合材料热导率Table 2 Thermal conductivity of erythritol/CNTs composites with random distribution

图7 赤藓糖醇/碳纳米管随机填充复合模型.（a）赤藓糖醇/碳纳米管（3根）复合材料随机模型；（b）赤藓糖醇/碳纳米管（5根）复合材料随机模型；（c）赤藓糖醇/碳纳米管（6根）复合材料随机模型Fig.7 Random filling model of erythritol/CNTs: (a) random filling model of erythritol/3 CNTs composites; (b) random filling model of erythritol/5 CNTs composites; (c) random filling model of erythritol/6 CNTs composites

2.5 声子振动态密度

对于非金属材料，声子作为热量传递的主要载体，承载着大量的能量.声子振动态密度（Vibration density of states, VDOS）可以得到原子的振动情况，利用声子振动态密度对材料的热导率变化机制进行分析是目前常用的手段之一[36-39].声子振动态密度由原子的速度自相关函数（Velocity autocorrelation function, VACF）傅里叶变换得到[40]：

式中，N是原子个数，是第i个原子在t0时刻的速度矢量，＜ ＞代表初始时刻为t0的时间平均，v为声子频率.

本文分别计算了赤藓糖醇以及碳纳米管在复合前后的声子振动态密度，如图8所示.碳纳米管在复合材料中多处声子振动峰值降低，在低频区尤为明显，而对于纳米碳材料而言，低频区声子振动具有较大的声子平均自由程，较长的能量传输距离可减少声子碰撞导致的热阻，对于热输运具有重要作用[35].由于与赤藓糖醇相互作用，碳纳米管声子振动受到抑制，导致其在复合材料中的热导率远低于独立的碳纳米管，从而复合材料的热导率仅在 100～101W·m-1·K-1量级.在赤藓糖醇中0～66 THz范围内的声子对其热导率起主导作用[28]，在此频率范围内，相比纯赤藓糖醇，复合材料中的赤藓糖醇声子振动在16、38和63 THz处得到了明显加强，振动峰值明显增高，碳纳米管的加入激发了赤藓糖醇中的声子热输运，在一定程度上增强导热.

图8 赤藓糖醇/碳纳米管复合材料声子振动态密度.（a）碳纳米管复合前后声子振动态密度；（b）赤藓糖醇复合前后声子振动态密度Fig.8 VDOS of erythritol/CNT composite: (a) VDOS of CNTs before and after compound; (b) VDOS of erythritol before and after compound

3 结论

（1）碳纳米管作为导热增强材料可有效提高赤藓糖醇的热导率，在其声子平均自由程范围内，赤藓糖醇/碳纳米管复合相变材料热导率随碳纳米管轴向长度增加而显著提高，同时随碳纳米管质量分数增大而提高.碳纳米管长度为8.6 nm，质量分数为13.35%时，复合材料沿碳纳米管轴向热导率可达到纯赤藓糖醇的6.5倍，平均热导率可达到纯赤藓糖醇的2.5倍.

（2）碳纳米管规则排列时复合相变材料热导率表现出明显的各向异性，由于引入界面热阻导致沿碳纳米管径向复合相变材料热导率反而低于赤藓糖醇，碳纳米管随机分布方式可有效解决热导率的各向异性，沿各个方向热导率均得到提升.

（3）由于碳纳米管与赤藓糖醇间的相互作用，碳纳米管的声子振动受到抑制，表现出远低于独立碳纳米管的热导率，但赤藓糖醇中多处声子振动被激发，增强了赤藓糖醇中的声子热输运，从而促进了热量传递.