大尺寸球形件的光笔式视觉测量系统设计＊

蒋灵搏 李云雷

（①山东工业职业学院，山东 淄博 256414；②山东理工大学机械工程学院，山东 淄博 255049）

球形结构的零件在航空航天装备、机械制造和精密仪器仪表等领域应用广泛，如航空发动机的角接触球轴承、硬密封球阀、球形铰链和球形曲柄曲轴等[1-3]。在某些特殊工业生产过程中，大尺寸的球形或非整形球面特征的零件也有较大需求，如高压天然气输送管道的球阀[4-5]，其直径约在100～1 016 mm；制造天线球面屏的大型球面模胎，其曲率半径可达12.8 m[6]。针对不同尺寸的球形零件，球径和球度误差的测量评定是进行产品质量控制的重要手段。

目前，球形零件的测量设备主要包括三坐标测量机、气动量仪、激光干涉仪以及激光跟踪仪等[7-8]。这些设备用于大尺寸的球形零件测量时，仍存在不足之处。三坐标测量机工作于实验室环境，无法应用于工业现场，其测头只能沿3 个坐标轴方向移动，自由度有限，受自身结构和测头长度制约，无法探测大尺寸整球面的底部区域，存在测量盲区，并且维护成本高。气动量仪和激光干涉仪仅适用于小尺寸球形构件的测量。激光跟踪仪可实现高精度大范围的三维点测量，但其价格昂贵，并且易受环境温度、压力等因素的影响。

综合上述问题，本文设计了一种光笔式视觉测量系统用于大尺寸球形零件的测量。在摄像机视场范围内，系统自带的光笔可以在三维空间内自由移动，光笔的针状测头能够探测到球形零件表面的任意点，并快速生成测点的三维坐标，进而拟合出理想球，计算获得球径和球度误差。

1 系统工作原理

光笔式视觉测量系统主要由摄像机、光笔和配套的图像处理软件组成，其工作原理如图1 所示。摄像机的空间位置固定，其坐标系为OC-XCYCZC，原点OC位于摄像机的光心。光笔上分布有共面的控制点，其自身坐标系为OP-XPYPZP，原点OP位于右下角的控制点处。

图1 光笔式视觉测量系统的工作原理

测量时，手持光笔在摄像机的视场范围内自由移动，光笔测头接触球形件表面的任意点，每接触一点拍摄一张像片，并保证像片内含有全部的控制点。利用图像处理软件提取出像片中每个控制点的像素坐标，它们在光笔坐标系的三维坐标已知，进而计算出光笔坐标系和摄像机坐标系之间的位姿关系，即旋转矩阵RPC和平移矢量TPC。假设光笔测头在自身坐标系OP-XPYPZP的坐标为 (XPh，YPh，ZPh)，则它在摄像机坐标系的坐标为

实际上， (XCh，YCh，ZCh)就是光笔测头接触的球面被测点在摄像机坐标系下的三维坐标。光笔测头每接触一点，分别对应不同的旋转矩阵RPC和平移矢量TPC，依据式（1）就可以计算出球面上所有被测点在摄像机坐标系下的三维坐标。

2 光笔设计

2.1 光笔结构

为了有效探测大尺寸球形零件表面的三维点，光笔设计成图2 所示的结构，包括定向棋盘格、金属测杆和针状探头三部分。定向棋盘格粘贴于平面精度等级较高的亚克力透明板上，保证所有角点共面，光笔坐标系原点OP位于图2 所示的角点位置，XP轴 沿水平方向，YP轴沿竖直方向，ZP轴按右手法则确定，每个小方格（包括黑色和白色）的尺寸为28.4 mm×28.4 mm，从而计算出所有角点在光笔坐标系的三维坐标，其ZP坐标均为0。金属测杆用于扩展测量范围，可以依据被测对象几何尺寸大小定制不同长度的测杆。针状测头与测杆螺纹连接，与球面三维点形成点接触，避免了球形测头产生的半径补偿误差。

图2 光笔结构

2.2 光笔标定

光笔标定是确定针状测头在光笔自身坐标系OP-XPYPZP的精确三维坐标。本文采用近景摄影测量方法[9-10]实现光笔标定，如图3 所示，手持摄像机从多个角度拍摄光笔的9 张像片，要求每张像片均包含完整的光笔图像。

图3 光笔的近景摄影测量

光笔标定的具体步骤如下：首先，在9 张像片内提取针状测头和图2 虚框内全部角点的像素坐标，并对每张像片提取的像素坐标进行匹配（按相同顺序排列）；其次，根据所有角点在光笔坐标系内已知的三维坐标和它们在每张像片的像素坐标，可以建立每个摄像机（亦称摄站）坐标系和光笔坐标系之间的转换关系（转换原理参考本文章节3），也就确定了所有摄站的空间位姿；最后，采用近景摄影测量中的光束平差算法，求出光笔的针状测头在其自身坐标系OP-XPYPZP的精确三维坐标，结果为（-200.328 mm，91.430 mm，-12.531 mm）。所有摄站的位姿和角点以及测头的空间分布，如图4 所示。

图4 摄站位姿和角点、测头的空间分布

3 坐标系的转换

在图1 中，要获得被测点在摄像机坐标系的三维坐标，关键是建立光笔坐标系和摄像机坐标系之间的位置关系，即计算出旋转矩阵RPC和平移矢量TPC。如图5 所示，物方平面是光笔棋盘格所处平面，任意控制点（即角点）为Mi，它们在像平面的像点为mi，坐标系转换的具体步骤如下：

图5 坐标系的转换原理

（1）像点的像素坐标转换至摄像机坐标系，并归一化处理。设像点的像素坐标为mi=[xi,yi]T(i=1,2,···,n)，并假设已对mi做了畸变矫正处理。再令摄像机的内参数矩阵为：

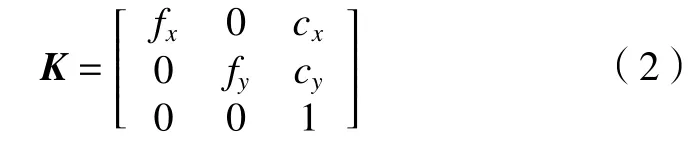
其中：fx、fy为 摄像机的主距，cx、cy为摄像机的主点坐标。

将像点mi转换至摄像机坐标系，并以主距为单位做归一化处理。令转换后的归一化坐标为则有

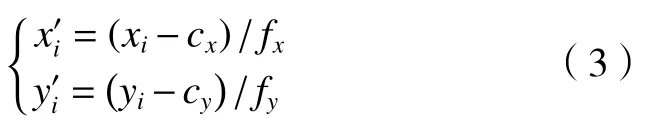
（2）构建物方平面与像平面之间的单应性矩阵。令控制点Mi在光笔坐标系的齐次坐标为=[Xi,Yi,0,1]T，则有

其中：λ为非零的比例系数。将旋转矩阵RPC的第i列元素表示ri，则式（4）演变为

n组对应点列写出 2n个线性方程，构建目标函数，采用Levenberg-Marquardt（LM）算法进行非线性优化求解，最终获得H的最佳近似解。

（3）确定RPC和TPC的近似解。将单应性矩阵以三个列向量的形式表达，即H=则旋转矩阵RPC的列向量和平移矢量TPC的计算公式为：

其中：“ ||” 代表向量的模，“ ×”代表向量的叉积。

（4）确定RPC和TPC的最优解。构造如下的目标函数

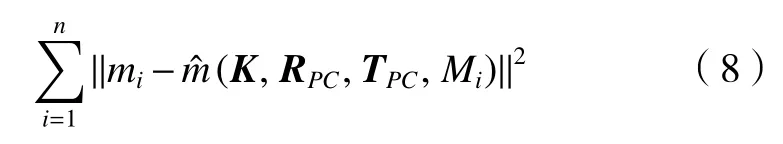
(K,RPC,TPC,Mi)是 物方平面控制点Mi依据近似的RPC、TPC和摄像机内参数矩阵K在像平面的重投影像素坐标，mi则是实际提取的像素坐标。式（7）是一个非线性最小化问题，代入RPC和TPC的近似解，再利用LM 算法获得它们的最优解。

4 实验

4.1 精度评价实验

本文选取高精度的光栅尺评价光笔式视觉测量系统的测量精度，光栅尺在1.0 m的行程范围内测量误差优于5 μm。实验设备包括已标定的摄像机（尼康D3200）、光笔、光栅尺（动尺和定尺）以及数显表。

如图6 所示，光栅尺动尺初始位置在最右侧，将数显表调零，然后让动尺向左移动一定距离，并由数显表读出，作为位移基准值。动尺顶部开有锥孔，在其移动的起点和终点，光笔分别探测锥孔尖端，以确保接触到同一点，同时由位置固定的摄像机拍摄两张像片，依据本文前述理论获得锥尖移动前后的两个三维坐标，进而计算出动尺的位移，作为光笔式视觉测量系统的测量值。实验共选择了3个基准值，针对每个基准值均测量5 次，测量结果如表1 所示。

表1 精度评价实验的结果

图6 精度评价实验的设备

实验中，摄像机距离光栅尺约1.8 m，视场范围约2 000 mm×1 500 mm。表中数据表明，在上述视场范围内，系统的相对测量精度约为0.05 mm/1.0 m，能够满足一般工业产品在加工制造过程中的几何精度要求。

影响该系统测量精度的主要因素包括：摄像机标定的精度、光笔标定的精度和图像处理过程中角点像素坐标的提取精度。通过选择尺寸更加精确的标定板，增加像片的拍摄数量等措施，进一步提高摄像机标定和光笔标定的精度。利用Harris 角点检测算法（精度0.03 像素）可获得光笔中定向棋盘格角点的精确像素坐标[11]。另外，还要保证测量环境具有足够的光照强度，以便获得清晰的光笔像片。若环境光线较暗，可在摄像机的闪光模式下拍摄。

4.2 测量实验

实验设备包括直径约为280 mm的大尺寸金属球、摄像机（尼康D3200）和光笔。摄像机固定于三脚架上，金属球固定于工作台，二者距离约为1.5 m。如图7 所示，手持光笔依次探测球的顶部和前后左右等区域，每接触一点，摄像机拍摄一幅像片，经图像处理后，计算出被测点在摄像机坐标系下的三维坐标。

图7 大尺寸金属球的测量实验

实验共提取金属球表面的160 个测点，并由这些点生成最小二乘拟合球，如图8 所示。具体数据如下：拟合球的球心坐标为（-32.632 mm，88.427 mm，1 171.249 mm），球半径为R=140.047 mm，被测点到球心的球半径变化区间为[139.346 mm，141.275 mm]，则金属球的球径误差为1.929 mm。

图8 提取的被测点和拟合球

5 结语

为了实现大尺寸球形件的球径、球度误差测量，设计了一种光笔式视觉测量系统。其中的光笔设计成点接触形式，避免了球形测头的半径补偿误差，并利用近景摄影测量方法完成光笔标定。提出了利用物方平面与像平面的单应性矩阵构建光笔坐标系与摄像机坐标系之间位姿关系的方法。基于光栅尺的精度评价实验表明，系统的相对测量精度为0.05 mm/1.0 m。同时，针对大尺寸金属球实现了球径和球度误差测量。