面向立体视觉结构光三维重建系统的点云误差补偿方法
2022-04-07刘忠强马嵩华胡天亮张桐嘉段岳飞
刘忠强 马嵩华 胡天亮 张桐嘉 段岳飞
(①山东大学机械工程学院,山东 济南 250061;②高效洁净机械制造教育部重点实验室,山东 济南 250061;③机械工程国家级实验教学示范中心,山东 济南 250061)
近年来,非接触三维重建技术应用于越来越多的关键领域,如航空叶片测量[1]和文物保护[2]等。在众多非接触三维重建算法中,立体视觉结构光三维重建技术结合了立体视觉技术和结构光技术的优点[3],重建效率高而且结构简单。立体视觉结构光技术中相机标定的精度决定了三维重建的精度[4],但是由于目前的相机标定模型和标定算法的局限性,相机的标定误差不可避免,而且相机的标定误差会在三维重建的过程中耦合和累积形成累积误差[5],另外当被扫描物体远离相机最佳焦距的情况下,此时成像也会引入误差[6]。减少或消除这些误差对提高三维重建的精度有重要的意义,因此,需要对这些误差进行分析和研究。
针对上述问题,许多学者展开了大量的研究,Zhang Z 提出了高度柔性的相机标定方法[7],但是该方法在进行相机标定的时是通过优化像素重投影误差来进行迭代计算,在立体视觉系统中,优化的目标和重建的结果不一致。为了解决这个问题,Cui Y 等人提出了一种针对立体视觉系统的标定方法[8],通过最小化重建点和参考点之间的距离误差来优化相机标定的内外参数,成功提高了系统的重建精度。但是上述的优化方法并不能完全消除误差。卞玉霞等人提出了双目系统的误差度量模型[5],运用矩阵微分理论分析了双目系统中存在的误差和误差的传播规律。但是由于畸变参数、焦距、相机间的相对关系都是独立的,难以去精确地评估和修正[9-10]。Sankowski W 等对立体视觉系统的测量不确定度进行了评估[11],通过标定板和通用激光测距仪粗略地标定了立体视觉系统在X、Y、Z三个方向的测量不确定度,但是该方法仅适用于室外立体视觉系统中,不适用于立体视觉结构光系统。Isa M A 等人使用激光干涉仪和直线模组对立体视觉系统的空间误差进行了测量和补偿[12],但该方法是通过直线模组的误差传递模型来表示立体视觉系统的误差,没有直接对立体视觉系统的误差进行测量。综上所述,针对立体视觉结构光技术的误差分析和补偿仍然没有良好的解决方案。
在数控机床系统中,空间误差标定和补偿应用广泛[13-16],而且效果明显。针对立体视觉结构光三维重建系统中存在的问题,将误差补偿思想运用到立体视觉结构光系统中,提出了一种面向立体视觉结构光三维重建系统的点云误差补偿方法。通过对重建的点云进行误差补偿,从而减少误差,提高三维重建精度,为后序的工件测量、加工等工序提供更高质量的数据。
1 整体框架设计
本文的总体研究框架如图1 所示,包括3 个部分:误差标定、建模和补偿。误差标定模块是根据立体视觉结构光三维重建系统的成像原理,设定了一个视场空间,并使用高精度的棋盘格和移动装置建立起这个视场空间内的特征点集,并提出了对应的误差计算方法,标定了该视场空间内离散特征点的误差。误差建模模块是使用拟合能力强大的神经网络来建立起该空间内的误差模型,从而通过误差模型可以得到该空间内任意一点的误差值。误差补偿模块是使用建立的误差模型对测量点云进行误差计算和误差补偿。
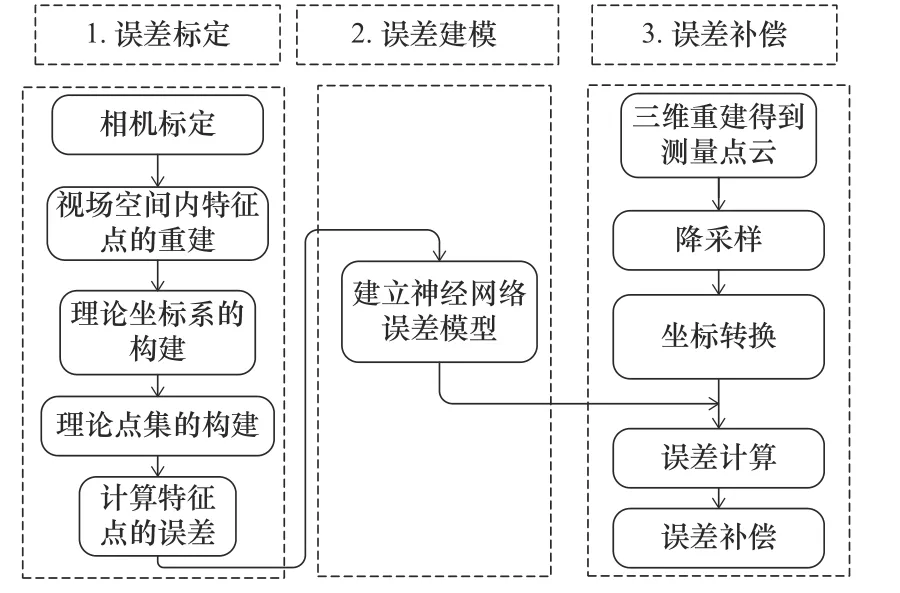
图1 整体框架
2 立体视觉结构光系统的误差标定
误差标定的思想是将视场空间分为多个立方体,立方体的顶点作为特征点,计算出每个特征点的坐标和误差,如图2 所示。
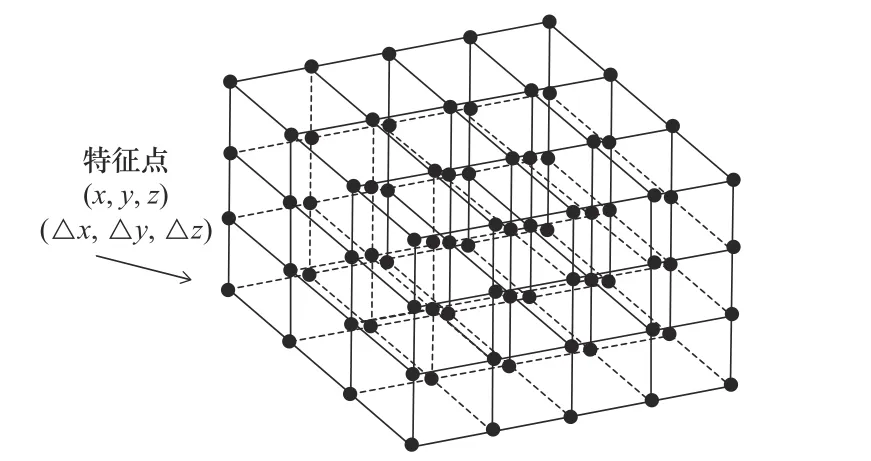
图2 测量空间特征点示意图
在立体视觉结构光系统中,投影仪仅用于向被测物体表面投射编码图案,无需进行标定[3],因此本文只对立体视觉系统的误差进行标定和补偿。
2.1 相机标定
本研究使用操作简单,精度高的张氏标定法[7]进行相机标定。
2.2 视场空间内特征点的重建
首先,设定了一个视场空间,该视场空间即标定空间。将立体视觉结构光系统放置于标定板正前方,调整相机焦距,使当前位置的标定板位于最佳焦距和视野内,在最佳焦距的位置前后距离为d的空间内构成的测量视场空间Λ,如图3 所示。
接下来,构建测量空间内的特征点集。重建图3所示的第一个位置的棋盘格的角点的点云,使用文献[17]的方法来进行重建,重建的过程主要包括立体校正、畸变矫正、亚像素角点提取、视差计算和点云重建等步骤。具体流程如图4 所示。
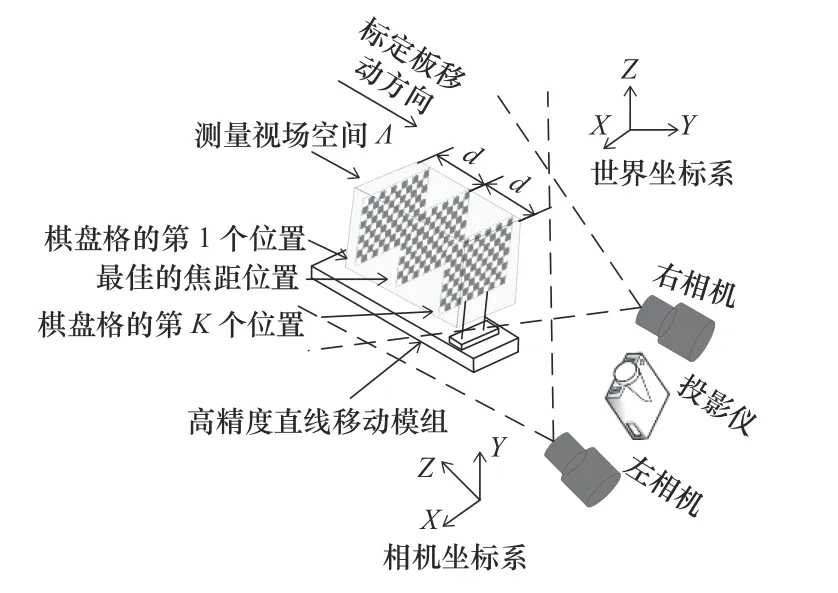
图3 测量空间内特征点构建示意图
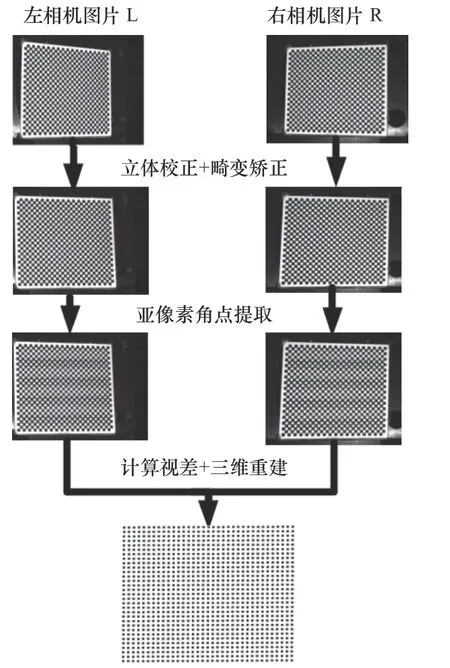
图4 棋盘格点云构建流程
最后,移动棋盘格并在每个位置进行棋盘格角点重建,获得整个空间内的特征点云。从第一个位置开始通过高精度直线移动模组带动棋盘格移动k次,则每次移动的距离为Δd=2d/k,则标定板的位置分别为(0,△d,···,m△d,···,(k-1)△d),共获得k幅在相机坐标系下的三维点集,设为(0Ωc,···,mΩc,···,k-1Ωc),这些点集称为特征点集,其中下标c表示位于相机坐标系下。重建出的特征点云集合如图5 所示。通过计算这些特征点的误差即标定了该空间内的误差分布情况。
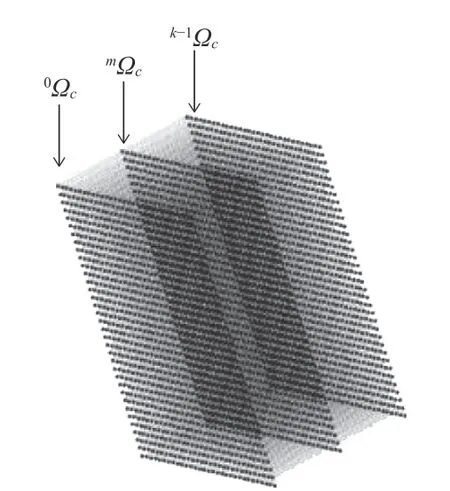
图5 特征点集示意图
2.3 理论坐标系的构建
为了计算特征点的误差,必须设定理论点作为标准,因此必须建立理论坐标系。理论坐标系的构建包括构建单位向量和设定原点。
单位向量的计算方法如图6 所示。在k幅点云(0Ωc,···,mΩc,···,k-1Ωc)中,在每幅点云中选取相同位置的一个点,对这些点进行最佳直线拟合,直线的方向设为理论坐标系的Z轴方向,设其方向向量为,如图6a所示。同理,在每幅点云中选择相同的行的点集,对选取得到得点集进行Ransac 平面拟合[18],平面的法向设为理论坐标系的Y轴方向,设其方向向量为,如图6b 所示。通过正交关系,则,如图6c 所示。则此理论坐标系的单位向量为接下来设定坐标原点。在k幅点云(0Ωc,···,mΩc,···,k-1Ωc)中 选取最佳焦距位置的点云mΩc建立理论坐标系,其中m=floor((k-1)/2),floor()表 示 下取 整 函数。在平面点云mΩc中,选择中间部分的某一点作为原点。为了计算每个特征点的误差,必须将位于相机坐标系下的特征点集转换到理论坐标系下,从而将两个坐标系统一。相机坐标系下的k幅特征点集(0Ωc,···,mΩc,···,k-1Ωc)可以通过式(1)转化到理论坐标系下为(0Ωu,···,mΩu,···,k-1Ωu),其中下标u表示位于理论坐标系下。相机坐标系下的原点转换到理论坐标系下为理论坐标系的原点,即=(0,0,0)。

图6 构建单位向量的示意图

2.4 理论点集的构建
在建立好理论坐标系后,为了计算每个特征点的误差,需要构建理论坐标系下的理论点集。构建理论点集的流程如图7 所示,分别为计算方向向量、计算基准行、平移基准行得到基准平面,最后平移基准平面得到理论点集。下面对这些步骤进行详述。
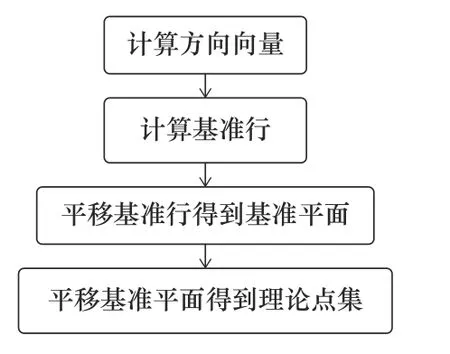
图7 理论点集的构建流程
2.4.1 计算方向向量
首先,取点集mΩu来计算理论点集的分布方向,计算方法如图8 所示。取该点云平面横坐标和纵坐标的点进行直线拟合并取平均值得到点集在二维平面内分布方向向量,设分别为,即
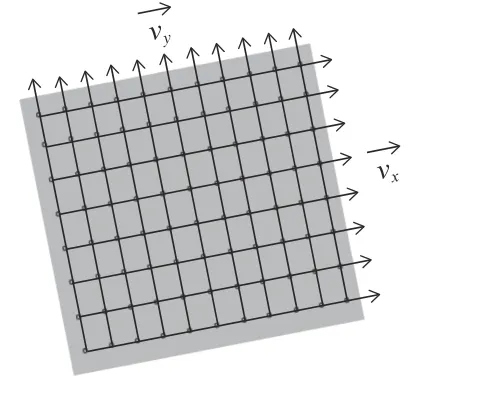
图8 计算方向向量
2.4.2 计算基准行

图9 构建理论点集的示意图
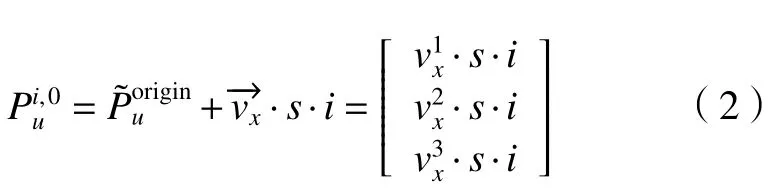
其中:s为标定板棋盘格的格子边长;i表示基准行上的第i个点。当计算沿着正方向的标准点的坐标时,取i=0,1,2,···,w-1-floor计算沿着反方向的标准点的坐标时,取i=-1,-2,···,
2.4.3 平移基准行得到基准平面
为了得到整个标准平面的点集,需要将基准行的点集进行平移,如图9b 所示。

2.4.4 平移基准平面得到理论点集
通过平移基准平面来模拟直线模组的带动标定板的移动过程,从而得到整个空间的理论点的分布。求取过程如图9c 所示。
首先,计算出特征点集在理论坐标系下的移动方向。在理论坐标系下的特征点集(0Ωu,···,mΩu,···,k-1Ωu)中,取每个平面相同的点进行直线拟合得到平面的移动方向
接下来,将基准平面点集mΨu沿着方向移动即可得到整个空间内的点集,对应的点的坐标由式(4)计算得到。

2.5 计算特征点的误差
特征点集(0Ωu,···,mΩu,···,k-1Ωu)和理论点集(0Ψu,···,mΨu,···,k-1Ψu)都位于相同的理论坐标系下,则误差可由公式(5)进行计算。
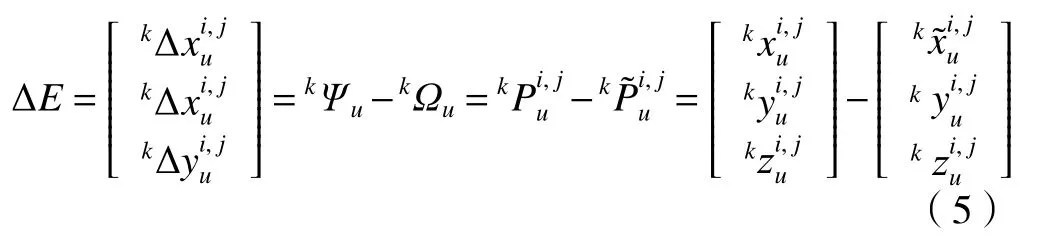
3 基于神经网络的误差建模方法
进行误差标定后,目前只能得到离散的特征点的误差,并不能得到整个空间内任意目标点的误差,因此需要进行误差的建模,拟合出整个空间的误差模型。针对这个问题,本文提出了一种基于多输入,多输出的前馈神经网络的建模方法。经过多次试验,确定了如图10 所示的网络结构,这个神经网络有3 个输入,分别是位于理论坐标系下的特征点在x、y、z这3 个方向的坐标值,有两个隐藏层,神经元的个数分别是14 个和3 个,同时有一个输出层,神经元的个数是3 个,该神经网络有3 个输出,分别是输入的坐标对应的在x、y和z这3 个方向的误差。
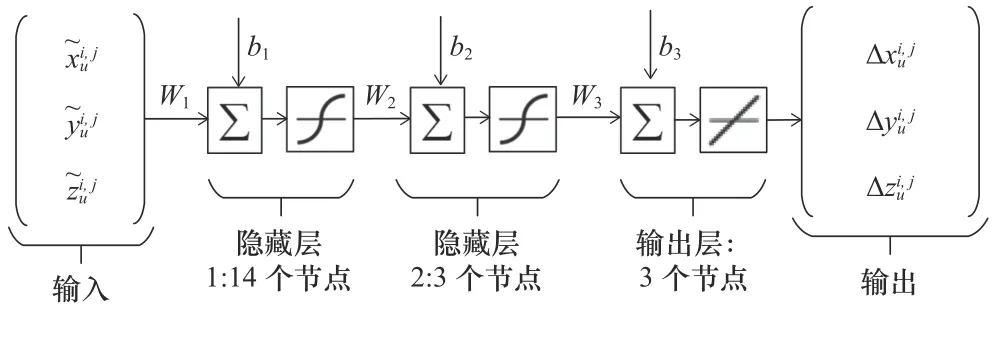
图10 神经网络示意图
4 立体视觉结构光系统的误差补偿
误差补偿流程如图1 所示。首先,使用文献[17]的立体视觉结构光三维重建方法对扫描的物体进行三维重建得到测量点云。
重建的点云中点的个数高达几十万个,这会大大降低后序点云处理的速率,所以需要进行降采样,本文使用的是基于体素网格[19]的降采样方法。
由于图10 所示的神经网络的输入和输出都位于理论坐标系下,所以在进行误差补偿时,需要将位于相机坐标系下的测量点云通过式(1)转换到理论坐标系下作为输入。
使用神经网络进行误差预测,计算公式如下:
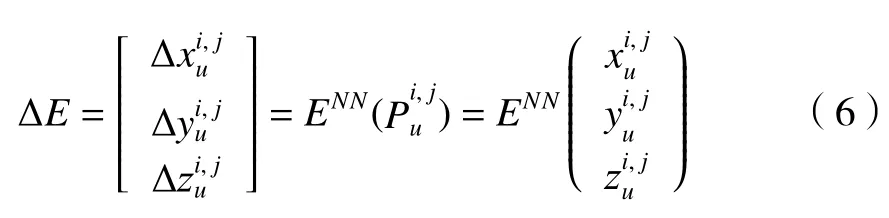
其中:ENN表示建立好的神经网络模型。
预测得到误差后,用下式进行误差补偿。
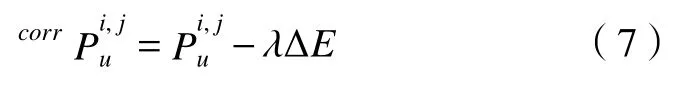
其中:表示经过补偿后的坐标,λ为矫正因子。经过试验,当 λ=0.2时能够取得最优的补偿效果。
5 实验验证
5.1 实验设计
立体视觉结构光系统如图11 所示,使用两个大恒HV1351UM 系列130 万像素的灰度工业相机和一个普通商用投影仪。

图11 立体视觉结构光系统
标定系统如图12 所示。选择重复定位精度很高的直线电机来带动高精度的标定板移动,保证移动准确。各部分的参数如表1 所示。
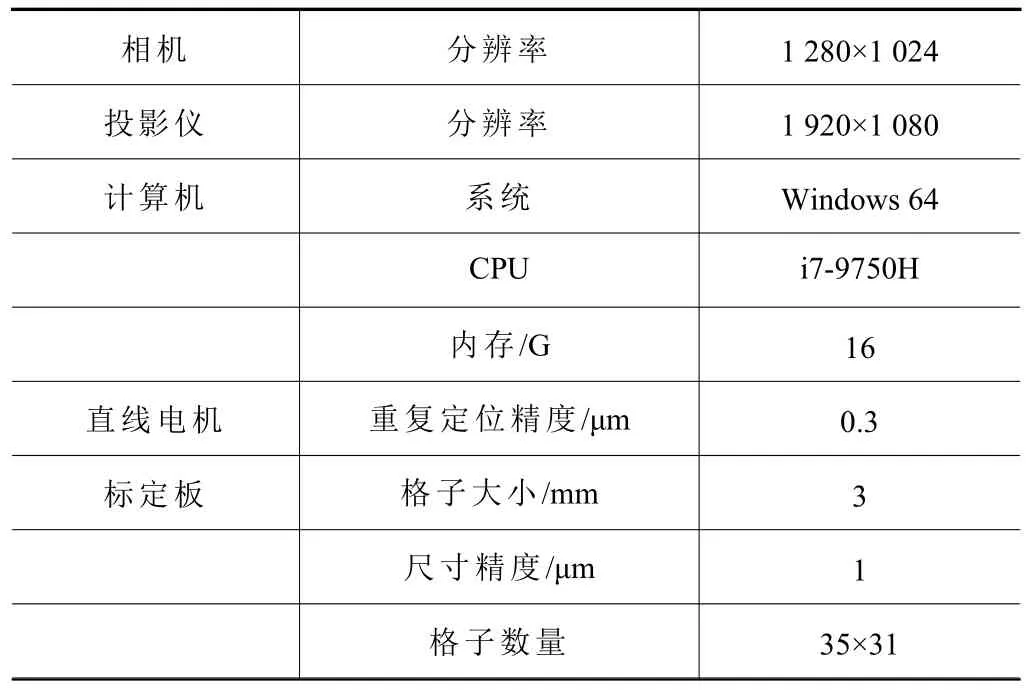
表1 参数列表

图12 实验装置示意图
首先,构建特征点集。首先确定标定范围空间,根据相机的焦距,选取标定板离扫描系统475 mm附近作为测量空间的中心,记录此时的位置P,并调整相机和投影仪的焦距,保证此时位于位置P的标定板处于相机的最佳焦距位置。取Z方向P点前后各25 mm的范围作为测量空间,在X方向和Y方向的范围由标定板的尺寸确定。
在图12 所示的Z轴方向的测量空间范围内,通过直线电机带动标定板在Z方向每次移动1 mm。在每个位置同时使用左右相机采集标定板图片得到一对图像 (Li,Ri),然后使用图4 所示流程对每对图像进行棋盘格的点云重建,得到特征点云iΩc。重复上述步骤50 次,得到50 幅点云,组成特征点的点云数据,如图13 所示(图中加粗标注了特征点集中的0Ωc,1Ωc,24Ωc,49Ωc这几个平面点集)。
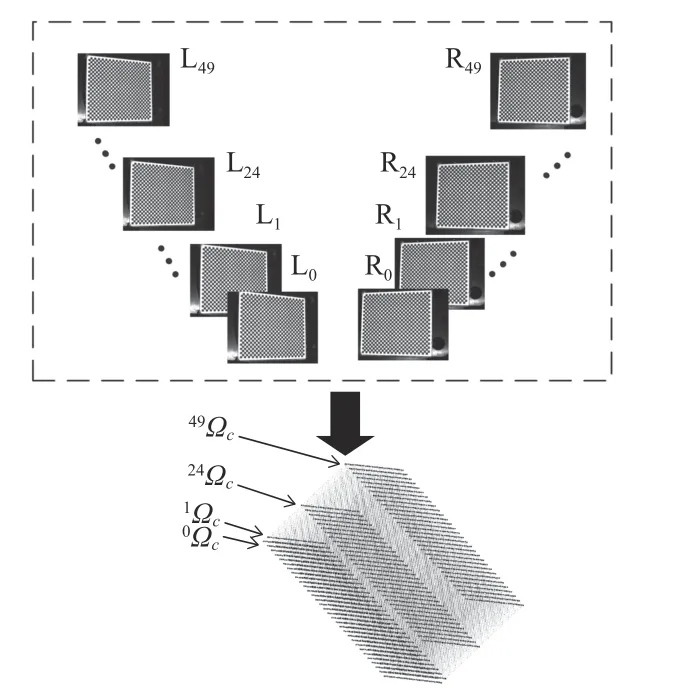
图13 特征点集构建示意图
使用第三部分所述的误差标定方法标定出每个特征点的误差,每个特征点在x、y、z这3 个方向的空间误差分布如图14、图15和图16 所示。
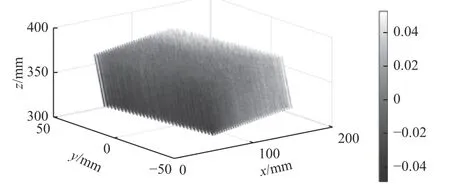
图14 每个特征点在x 方向的误差Δx

图15 每个特征点在y 方向的误差Δy
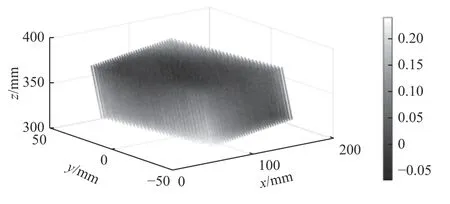
图16 每个特征点在z 方向的误差Δz
使用MATLAB 建立了如图10 所示的神经网络并进行训练,训练结果如图17 所示,训练集和验证集的损失非常相近,预测精度满足要求。
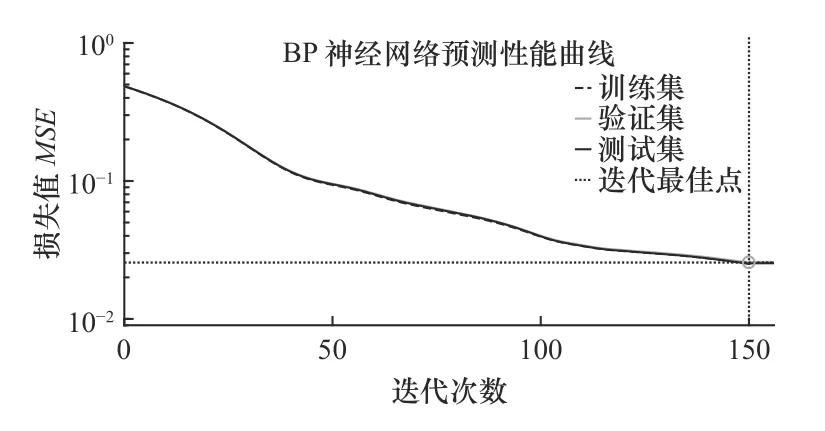
图17 神经网络预测性能曲线
得到误差模型之后,使用该模型进行误差计算和误差补偿。
5.2 实验结果和分析
2002 年,德国发布了面扫描系统的精度评价标准“VDI/VDE 2 634 PART II”,这一标准成为商业扫描系统的精度认证标准。该标准使用标准球进行空间误差评估。本文使用图18 所示的标准陶瓷球来进行精度评价。其中,对单球点云计算直径误差,对双球点云计算球心距误差。其中单球的标准直径为38.104 6 mm,双球的球心距标准值为60.008 2 mm。

图18 标准陶瓷球
使用第五部分所述的方法进行重建和补偿。首先,使用文献[17]所述的立体视觉结构光三维重建算法对采集的结构光编码图片进行处理和三维重建,得到测量点云;接下来,对测量点云进行降采样,降低点云密度,并将点云转换到理论坐标系下;最后,在补偿空间中使用神经网络误差模型对测量点云进行误差计算和补偿。具体流程如图19 所示(以单球为例)。
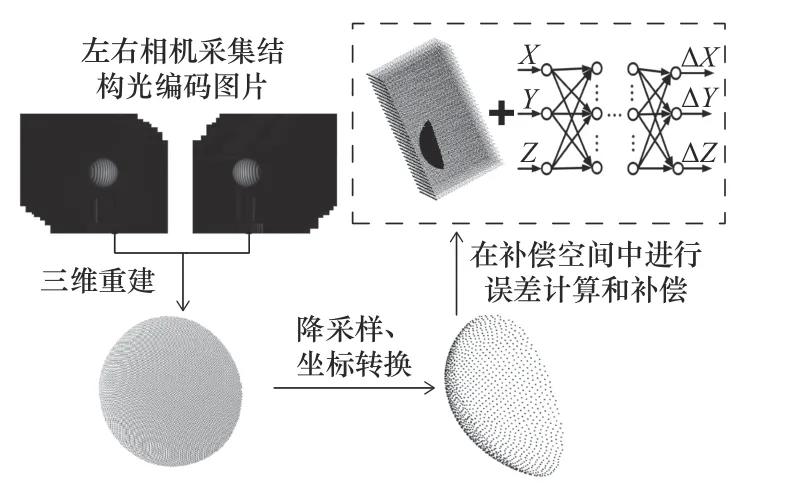
图19 误差补偿流程
为了保证实验结果的一般性,对单球进行了6组误差补偿实验,对双球进行了3 组误差补偿实验,并在重建时保证球体位置位于已经标定的测量视场空间范围内,如图20 所示。

图20 位于标定空间内的多组点云
使用GeomagicControl 软件分别对误差补偿前和补偿后的标准球点云数据进行拟合和测量,如图21 所示。测量结果如表2和表3 所示。

图21 点云的拟合测量
从表2和表3 可以看出,经过误差补偿以后,球直径误差平均减少了51.96%,球心距误差平均减少了14.16%,精度提升效果明显。验证了本文算法的有效性和可行性。
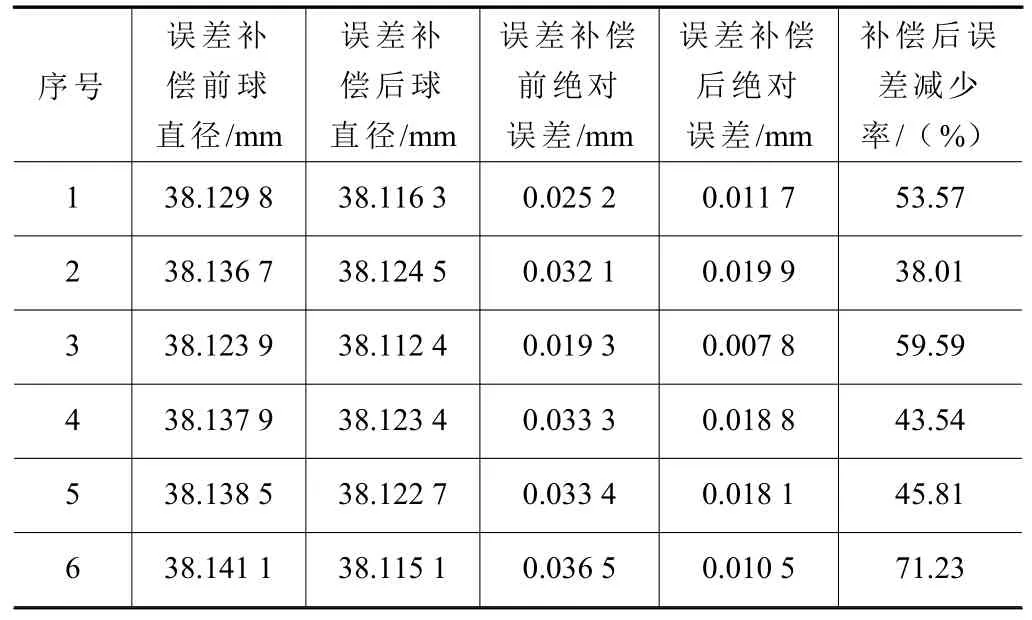
表2 误差补偿前后的球直径误差对比
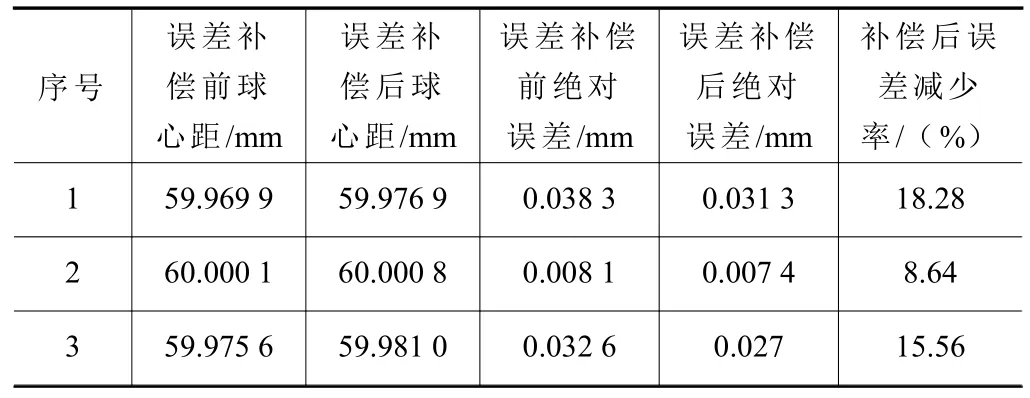
表3 误差补偿前后的球心距误差对比
6 结语
本文提出了面向立体视觉结构光三维重建系统的点云误差补偿方法,该方法分为误差标定、误差建模和误差补偿3 部分。使用棋盘格和高精度的移动模组得到空间内离散特征点的误差值;进而使用神经网络进行误差拟合得到误差模型;最后,利用误差模型进行误差补偿。实验结果表明,经过误差补偿,球直径重建误差平均减少了51.96%,球心距重建误差平均减少了14.16%,精度提升效果明显。未来将重点研究更灵活的误差标定方法和补偿方法,从而进一步提高本文算法的灵活性和鲁棒性。
