4-URU 柔性并联机构构型设计及支链刚度分析*
2022-04-07张旺旺薄瑞峰黄道阳陈振亚
张旺旺 薄瑞峰 黄道阳 陈振亚
(中北大学机械工程学院,山西 太原 030051)
随着科学技术的发展,精密加工技术越来越成为制造业发展的重要因素,从而导致对于定位技术的精度要求变得更高。目前,传统刚性并联机构的工作性能无法满足当下精密定位技术的快速发展,在高精密、微型机械等高性能要求下缺陷日益明显。而柔顺机构的出现则从机械设计这一根本角度为解决这些问题提供了新的、更彻底的方法,为实现高精密定位平台的设计与研究提供了理论依据。有学者提出通过将柔性铰链理论与刚性并联机构相结合,采用柔性铰链代替传统运动副的方法构建相应的柔性并联机构。和传统刚性并联机构相比,柔性并联机构通过构件自身弹性形变来实现机构的主要运动和功能。也正是因为在结构上减少了运动副,因此柔顺机构在构件的数目上就比传统机构少了很多,很大程度上降低或消除了上述问题。因此,将柔顺并联机构作为传动构件引入精密定位平台进行设计与研究具有重要意义[1-5]。近些年来,国内外相关学者结合柔顺机构理论与并联机构理论对柔顺并联机构有了更深入的研究。Wang R Z等基于六支链柔性并联机构的四自由度定位平台的设计及刚度建模[6],Yu H T 等基于柔度矩阵法对3PPR 平面并联机构设计及运动学分析[7],吴小川设计了一种新型六自由度柔顺并联机构[8],孙慧设计了3-RPC 柔顺定位平台[9]。目前,在对柔顺定位平台的研究中,刚度是研究和设计柔性并联机构的重要指标之一,在很大程度上影响着柔性并联定位平台的精度。因此,亟待提出一种新型求解支链刚度的优良方法。
本文利用螺旋理论[10]对4-URU 刚性并联机构的自由度进行分析。同时,利用柔性铰链替换法设计出相应的4-URU 型柔性并联机构。其次,在柔性铰链刚度矩阵基础上,利用矩阵转换求得支链中各铰链刚度矩阵[11],再利用有限元理论分别求得支链各柔性杆刚度,通过线性叠加求得支链的总刚度矩阵。最后通过理论计算并用ANSYS 软件对模型进行仿真分析,比对理论计算和仿真结果,验证该方法的可行性。为进一步研究柔性并联定位平台的精度问题提供理论依据。
1 4-URU 并联机构自由度分析
4-URU 刚性并联机构由4 条完全相同的URU分支链分别连接上下两平台构成。如图1 所示,每条支链由与上下两平台相连的虎克铰(U 副)及连接两连杆的转动副组成,相当于每条支链包含了5个单自由度的转动副,其中第1 个转动副与下平台(定)垂直,中间3 个转动副相互平行,第5 个转动副与上平台(动)垂直,初始位置时上平台和下平台相互平行。

图1 对称四自由度4-URU 并联机构构型
针对此机构的自由度,选取1 个分支链进行分析,如图2 所示,以$i1和$i2的交点O为坐标原点建立支链坐标系O-xiyizi,则URU 支链运动副的运动螺旋为:
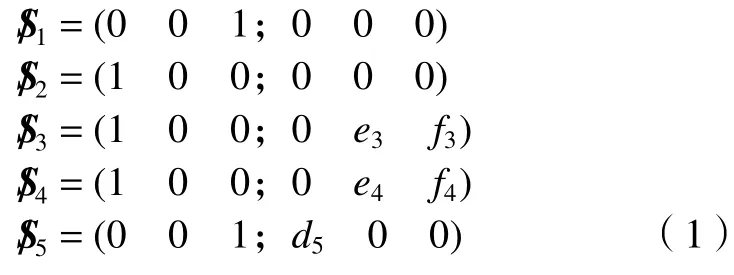

图2 4-URU 分支
为求此五系螺旋的反螺旋,我们根据螺旋互易积为零的原理进行代数求解得到其反螺旋为$ir=(0 0 0;0 1 0),根据求出的反螺旋不难看出,该支链的反螺旋为沿yi轴方向的约束力偶,即为沿虎克铰十字头的法向方向,在图2 中用双向箭头$ir表示此约束力偶。该机构4 条支链完全相同,且提供4 个位于同一平面(动平台)上的约束力偶,由同一平面内的4 个约束力偶仅有两个线性无关可知,此机构具有2 个冗余约束,4 个约束限制了该机构动平台绕x、y轴的的转动,故机构具有沿x、y、z轴的移动和绕z轴的转动。
2 空间4-URU 型柔性并联机构设计
现基于4-URU 刚性并联机构的要求,设计与其相对应的柔性并联机构。完全按照刚性的并联机构要求设计相应的柔性支链,最后通过同刚性并联机构相同的组合方式组合成为最终结构。在设计过程中,最终柔性并联机构各柔性支链的相对位置与刚性并联机构一致,各柔性支链运动副及其运动副位置与相应刚性并联机构对应、严格按照刚性并联机构支链的构型特点和运动副运动轴线间的关系。根据之前分析的4-URU 并联机构的构型特点设计与之对应的URU 型柔性支链及4-URU 型柔性并联机构如图3、4 所示。

图3 URU 支链三维图

图4 4-URU 柔性并联机构
3 4-URU 型柔性并联机构的支链刚度分析
为了能够求得柔性并联机构的整体刚度,必须先求得单条支链的刚度,从而推导出整体刚度,最终通过整合得出柔性并联机构整体刚度。下面对支链I 进行刚度求解,先把支链I 分为6 个部分,在柔性转动副刚度矩阵基础上分别求得各铰链刚度KJ,再利用单元刚度矩阵分别得出柔性杆各部分单元刚度矩阵KG,然后把铰链刚度KJ和6 个柔性杆部分的单元刚度矩阵KG叠加,从而得出支链的总刚度矩阵K=KJ+KG。
3.1 支链铰链刚度
支链I的结构为U(2R)-R-U(2R)结构,其中A、B、C、D、E均为柔性转动副,具体结构如图5 所示。
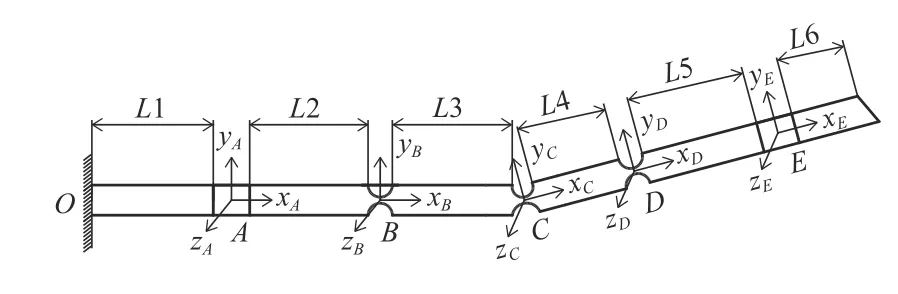
图5 支链断面结构
O点为固定一端,假设在E点处受载,可以简单得到A、B、C、D、E点的局部坐标系分别AxAyAzA、B-xByBzB、C-xCyCzC、D-xDyDzD、E-xEyEzE,文献[11-12]介绍了如图6 为标准的柔性铰链刚度矩阵KR:
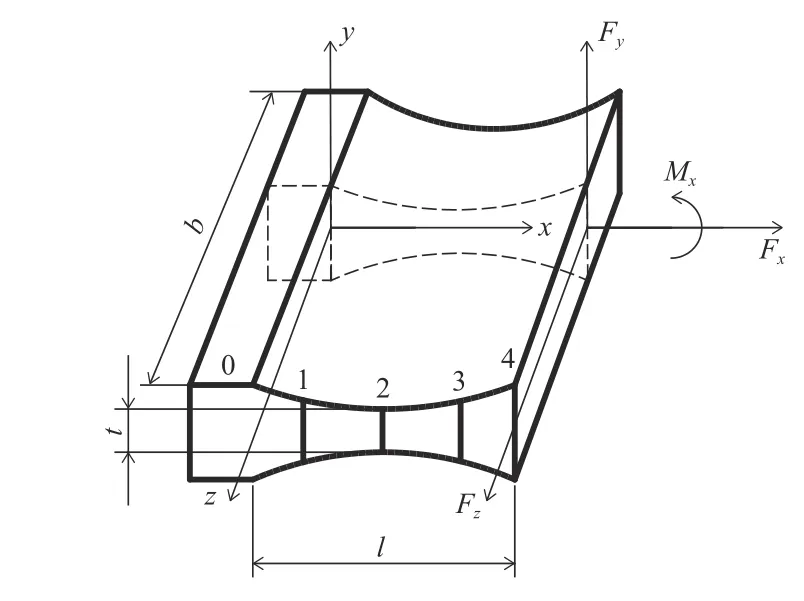
图6 柔性转动副结构尺寸

式中:E为柔性铰链的材料弹性模量;t为点2 处铰链横截面厚度、t1、t4分别为点1、4 所在铰链横截面的厚度。
由于柔性并联机构的主要目的是弥补常规刚性并联机构在高精度运动上的不足,该并联机构所受外载是静载荷或者载荷变化较小,运动缓慢,对于速度、加速度的变化情况可忽略不计,因此该结构主要对其静刚度进行研究分析。
如图5 所示,我们规定B-xByBzB坐标系相对于A-xAyAzA坐标系的转化矩阵为H1,C-xCyCzC坐标系相对于坐标系A-xAyAzA坐标系的转换矩阵为H2,DxDyDzD坐标系相对于A-xAyAzA坐标系的转化矩阵为H3,E-xEyEzE坐标系相对于坐标系A-xAyAzA的转换矩阵为H4,其中转换矩阵:
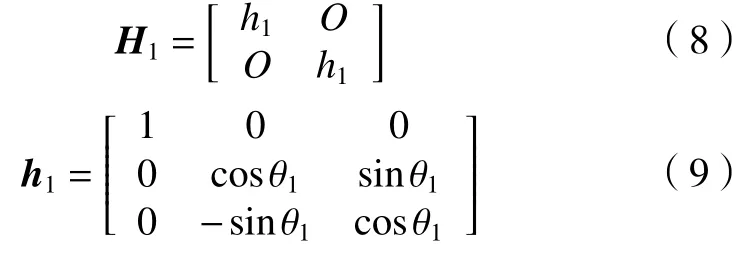
式中:H1为坐标变换矩阵;h1为坐标变换中的子矩阵,同理可推导出转换矩阵H2、H3、H4,即可以分别求得各柔性转动副刚度在A-xAyAzA坐标系中的不同表示,则点B处柔性铰链刚度在A-xAyAzA坐标系中可表示为:

同理可知,点C处柔性铰链刚度经过H2的矩阵转换后,其表达式在A-xAyAzA坐标系中为:

点D处柔性铰链刚度经过H3的矩阵转换后,其表达式在A-xAyAzA坐标系中为:

点E处柔性铰链刚度经过H4的矩阵转换后,其表达式在A-xAyAzA坐标系中为:
2011年 3月 27日凌晨 5点,李阿姨在家人的陪伴下平静地走了,女儿和老伴没有呼天抢地,没有悲痛欲绝,只是默默地收拾了东西,把一个干净的病房留给了我们。知道现在每次有患者提到“望路”的话题,我都会想起李阿姨。面对生死,从容是一种多么难得的品质。它让一个普通的老人高贵地离开人世,留给周围人都是美好的回忆。

通过以上求解的式子可求得点E处的局部铰链刚度总和为A、B、C、D、E处的5 个转动副在A-xAyAzA坐标系中的总和为:
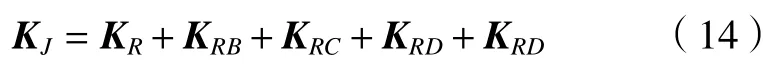
所求KJ即为支链各铰链A、B、C、D、E处铰链刚度之和。
3.2 支链单元刚度
有限元应分析问题时,首先就是要将其离散化,用离散化模型来代替原来的连续体。本文釆用的离散化方式是将除弹性铰链外的其他弹性连续体结构离散成三角形单元,应用最小势能原理推导了单元刚度■矩阵,并且该最小单元为三角形。其表达式为:Ke=由于材料是均质单元,弹性矩阵D元素为常量,并且对于平面三角形单元,B矩阵中的元素也是常量。单元的面积是dxdy=Δ,故上式的单元刚度矩阵亦可表示为如下形式:Ke=BTDBtΔ。对于平面三角形单元,其单元刚度矩阵即可表示为:

在有限元基本原理中,刚度矩阵的组集至关重要,在完成单元分析后,需要将单元组集组合起来,从而构成总的有限元分析方程。目前有很多方法适用于将单元刚度矩阵组合在一起形成总单元刚度矩阵,有直接组集法、转换矩阵法等,本文采用转换矩阵法进行求解。采用矩阵转换法求解支链柔性杆刚度矩阵时,最关键的是需要简单求解每个单元的转换矩阵,利用所求转换矩阵对每个单元刚度矩阵进行变换,从而通过叠加求得支链柔性杆总刚度矩阵。
在求解工程中,单元总刚度矩阵具有奇异性,因此需要引入边界约束条件、消除结构的刚体位移来实现。本文采用去掉边界条件中位移为0的行和列,这样会得到减少了阶数的矩阵,达到消除刚度矩阵奇异性的目的。得到最终引入边界条件修正后的有限元方程,由于引入了边界条件,即可直接进行求解。
4 理论计算结果及其ANSYS 分析
为了验证计算结果的正确性,下面进行对理论结果的仿真验证,将已知条件代入以上公式。
已知机构材料为65Mn(弹簧钢),其弹性模量:E=207 GPa;泊松比u=0.3;密度ρ=7 850 kg/m3。支链各部分结构详细尺寸如下:b=30 mm,t=4 mm,
4.1 理论计算结果
虚功原理又称虚位移原理,该原理在静力学分析中处于重要地位。虚功原理可作如下表述:“弹性结构处于平衡状态的充分必要条件是,对于任意微小的虚位移,外力所作的总虚功与其内部所积累的虚变形势能相等,即作用于系统的主动力所作的虚功之和为零”。则根据虚功原理和胡克定律可得[13]:

其中:F表示所受的外载荷力,K表示机构的整体刚度,q表示机构末端的位移。因此可得支链末端处的变形为:

将参数代入公式经理论计算后求得支链柔性铰链转动副的刚度矩阵及支链柔性杆单元刚度矩阵为:

将所求铰链刚度矩阵KR和单元刚度矩阵Ke经过线性叠加可得:
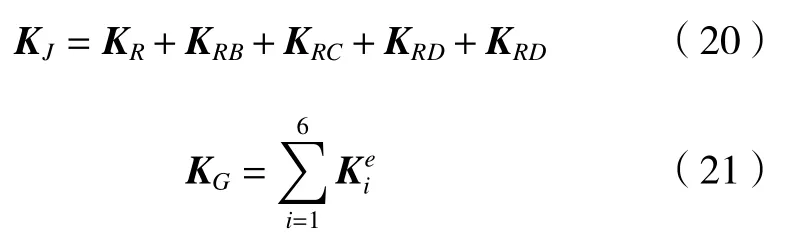
则支链的总刚度矩阵:

假设此时在E点末端处的x、y、z方向各施加100 N的等效力F,即F为[100 100 -100 0 0 0]T,将其相关参数代入上式:q=K-1F,最终求得q=[0.112 1 0.684 6 -0.109 2 0.626 2 0.255 8 0.576 9]×10-4mm,这样我们可以简单看出该支链在X、Y、Z方向产生的变形分别是1.112 1×10-5mm、6.846×10-5mm、-1.092×10-5mm。
4.2 ANSYS 仿真分析
针对上文所述的尺寸参数建立同等尺寸的SolidWorks 三维模型,然后导入ANSYS 进行分析,分析前需要进行一些材料参数的设置:定义机构材料属性、单元类型、网格划分等。在施加载荷时,将机构固定基座的自由度设置为0,外载荷施加在支链末端中心处,即X、Y、Z轴方向分别各施加100 N的外力。接下来就可对机构的三维模型进行简单计算和后处理分析,即可得到软件计算分析后的机构总位移应变图和分位移应变图如图7 所示。

图7 位移应变图
通过图7 我们可以清晰地看到其结构末端处在X、Y、Z方向的形变分为3.111×10-4mm、3.552 6×10-3mm、2.088 2×10-5mm,与理论计算值相接近。模拟结果与计算结果有误差是因为在将刚性并联机构转化为柔性机构过程中存在尺寸误差导致结果略有偏差,因此在实际加工使用时,应进行局部矫正。
5 结语
本文通过螺旋理论对4-URU 并联机构进行自由度分析,然后在此基础上设计出柔性并联机构。在柔性转动副刚度矩阵,单元刚度矩阵的基础上,将结构已知尺寸参数代入铰链刚度矩阵和单元刚度矩阵中,求得到4-URU 型支链总刚度矩阵,然后将所求支链总刚度矩阵、作用在支链的外载荷F代入虚位移和胡克定律的变形式中,从而得出支链在X、Y和Z轴方向的具体应变数值,最后利用ANSYS 软件对其进行仿真从而得出仿真结果。仿真结果表明,计算得出的支链末端变形量与ANSYS软件仿真结果接近。验证了该方法求解支链刚度的有效性,为利用该方法求解全柔性并联机构整体刚度提供理论依据,为超精密定位平台的精度研究提供了帮助。
