基于机器视觉的吊弦动态抬升量测量方法
2022-04-07许一统李红梅
阮 杰,龙 鹏,许一统,李红梅
(1. 武汉理工大学现代汽车零部件技术湖北省重点实验室,湖北武汉 430070;2. 中铁第四勘察设计院集团有限公司电气化设计研究院,湖北武汉 430063)
高速列车主要通过受电弓与接触线的相互接触[1]获得动力,以维持高速运行。受电弓的高速滑行会给整个接触网系统带来动态冲击,这种动态冲击的积累是造成接触网零部件疲劳损伤的主要因素之一。吊弦是连接承力索与接触线的关键部件,随着线路运营时间的增加,吊弦的疲劳寿命问题成为研究热点。通过研究受电弓滑过时吊弦在接触线侧线夹处的动态抬升量(简称吊弦动态抬升量),可以为弓网仿真计算[2]提供试验验证依据;通过研究吊弦动态抬升量随时间的变化曲线,可以为研究弓网接触关系、确定吊弦的疲劳载荷[3]提供实测数据,进而为吊弦的可靠性定量评估提供重要的支撑。
传统的吊弦动态抬升量测量方法大多数都是在定位点处采用接触式测量的方式进行。德国采用一种固定接触式的方案[4]在定位点处对吊弦动态抬升量进行测量,该方案利用带预张力绳索的定位器与电压表相连并在支持装置处固定,监测抬升量的变化;日本采用角位移传感器[5]通过细线与定位器端部相连,测量定位器端部的振动量,从而获取吊弦动态抬升量。接触式测量虽然精度较高,但是操作困难,并且只能局限于测量定位点处的抬升量,对于吊弦在接触线侧线夹处的动态抬升量,很难采用接触式的方式进行测量。
采用非接触式的测量方法不仅能够快速地对吊弦动态抬升量进行测量,而且操作方便,安全性更高。多位学者都对接触网参数的非接触式测量进行过研究。占栋等[6]基于车载双目线阵主动摄像机技术,实现了接触网拉出值等几何参数的测量;刘显录等[7]基于车载激光雷达以并行扫描的方式对接触网高度进行循环扫描测量;周威等[8]基于多目立体视觉提出非接触式测量方法,用于接触网几何参数的测量;Zhan 等[9]采用双目线阵相机,基于机器视觉的方法对接触网几何参数进行非接触式测量。这些研究方法都是采用车载相机或者传感器基于机器视觉实现的,以获得接触网的静态或动态参数。由于测量设备跟随检测车辆运动,对于接触网某一位置只能获得该点在检测车辆通过时刻的参数。虽然机器视觉技术已经广泛应用于铁路相关检测领域[10-17],但是对吊弦动态抬升量进行定点实时测量的研究较少。
本文首先采用鼠标交互的方式选取用于测量吊弦动态抬升量的初始模板和初始测量点,基于二维离散余弦变换和哈希算法进行模板匹配,实现测量点的快速跟踪并对测量点的像素坐标进行提取,其次建立测量模型,然后进行摄像机内参标定和坐标系的逆变换求解,最后推导出像素坐标和实际位移之间的转换公式。基于此方法,测量吊弦动态抬升量。
1 吊弦测量点像素坐标的提取
在基于机器视觉的测量方法中,首先需要在吊弦上定位测量点的初始位置,然后对测量点进行跟踪,从而提取测量点的像素坐标。目前很多研究方法都是通过在测量物体上贴目标靶标[18]进行测量点的定位跟踪,该方法虽然精度较高,但是在吊弦上贴目标靶标操作困难,并且很可能对线路的正常运行产生影响。针对当前的测量点定位跟踪方式无法有效地用于吊弦测量的问题,提出了一种基于模板匹配的测量点定位跟踪方法。
1.1 吊弦测量点的定位
首先,通过鼠标交互的方式在视频流的第1 帧图像上框选1个合适的测量区域,该区域需要包含吊弦在接触线侧的线夹,将该区域定义为初始模板图像,记录其宽度和高度。该模板图像的中心点即为初始测量点P1,记录其像素坐标。包含初始模板图像的第1 帧图像如图1所示。图中:蓝色矩形框包含的区域即为初始模板图像。

图1 包含初始模板图像的第1帧图像
确定初始模板图像后,将该模板图像中每个像素点颜色的R(红)、G(绿)和B(蓝)3 个像素值分量进行加权平均,获得灰度化后的初始模板图像,使每个像素点的像素仅包含0~255 中的某个数字,降低后期的运算量。
1.2 吊弦测量点的跟踪
1 张图像包含的信息可以由各种不同频率的信号组成。图像中,强度(亮度/灰度)变化比较平稳的区域如背景等大色块的区域主要由低频信号组成,低频信号能够描述图像的普遍信息;而对于边缘、尖角等亮度突变的区域主要由高频信号组成,高频信号能够描述图像的细节信息。图像中大部分的区域都是由低频信号组成的,因此可以通过获取低频信号还原图像的信息,减少图像的处理量。基于二维离散余弦正变换(Two Dimensional Discrete Cosine Transform,2D-DCT)[19],可以将图像的数字信息由像素域转换到频率域。二维离散余弦正变换公式为
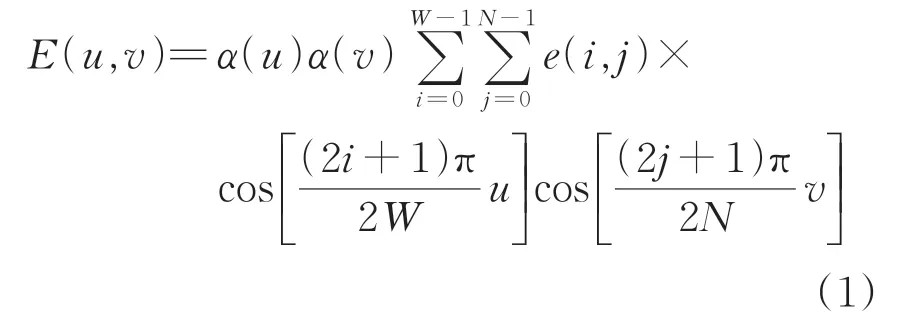
式中:E(u,v)为经过二维离散余弦正变换后频率域的元素,即灰度图像的频域矩阵E在(u,v)位置处的元素;e(i,j)为空间域中的二维向量元素,即灰度图像的数字矩阵e在(i,j)位置处的元素;u=0,1,…,W-1,v=0,1,…,N-1,为频率域采样值;i=0,1,…,W-1,j=0,1,…,N-1,为像素域采样值;W为输入图像的宽度;N为输入图像的高度;α(u)和α(v)分别为u和v的补偿系数。
二维离散余弦逆变换公式为
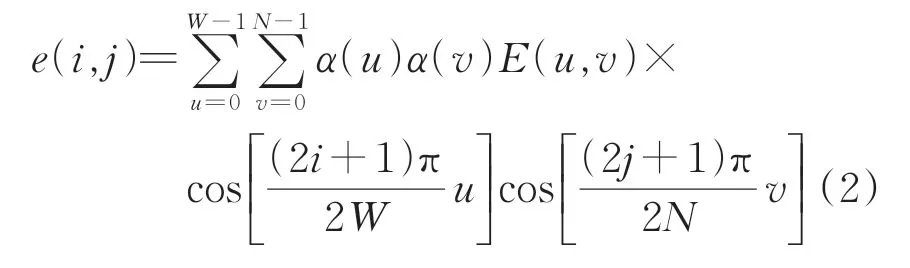
通过式(1)可以将灰度图像的信息从像素域转换到频率域,用1个2D-DCT 频域矩阵E表示灰度图像的高频信息和低频信息。
二维离散余弦正变换前后图像如图2所示。从图2可以看出:图像的左上角集中了图像大多数的“能量”,而越靠近左上角的位置频率越低,因此图像中大部分的信息都集中在了频域图的左上角部分。

图2 二维离散余弦正变换前后图像
截取频域图左上角的低频信息,代入式(2)可以将图像频率域的信息还原为像素域信息。二维离散余弦逆变换前后图像如图3所示。从图3可以看出:仅使用部分低频信号就可将图像进行还原,且保留大部分有效信息。

图3 二维离散余弦逆变换前后图像
通常为了简化2D-DCT 计算量,会将图像的尺寸大小压缩成(32×32)像素,然后再对图像进行2D-DCT 变换,并截取频域图像左上角(8×8)像素的区域,即大多数低频信号所在的区域,组成1 个低频系数矩阵;最后,将大小(8×8)像素的低频系数矩阵代入式(3)计算其哈希值。

式中:λ为由0和1组成的哈希值;Hash(·)为哈希函数;I为输入图像在频率域左上角的大小(8×8)像素的低频系数矩阵。
为实现测量点的跟踪,首先将初始模板图像的信息转换为大小(8×8)像素的低频系数矩阵,将低频系数矩阵代入式(3)计算其哈希值记为λ1;然后,采用滑动窗口法,在输入视频流的第2 帧图像内提取子窗口图像,提取的子窗口图像尺寸与初始模板图像的尺寸相同,用相同的方法计算子窗口图像的哈希值,并将子窗口图像的哈希值与初始模板图像的哈希值λ1进行位匹配,计算二者不同位数的数量,定义为汉明距离;最后选取汉明距离最小的子窗口图像作为最优匹配图像,记最优匹配图像的哈希值为λ2,将λ2与第3 帧图像中子窗口图像的哈希值进行位匹配,寻找出最优匹配图像并记录其哈希值λ3,以此迭代,直到寻找出所有图像的最优匹配图像为止。采用该模板匹配方法,可实现对每帧图像中最优匹配图像(即汉明距离最小的图像)的寻找,通过定位最优匹配图像的中心点即可实现测量点的跟踪。
由于匹配过程中加入了很多无关的背景图像,因此该方法的匹配时间较长。为了加快匹配速度,提出了一种基于前1帧图像测量点位置的局部域匹配方法。首先,定位第1帧图像中选择的初始模板图像的中心,并以该中心为基础建立1个局部域作为第2 帧图像的扫描区域,该局部域的宽和高需要大于初始模板图像的宽和高并且可以根据视频的帧率人为选取;然后,在局部域中采用滑动窗口法提取子窗口图像并进行上述模板匹配,寻找出最优匹配图像,并以该图像的中心点为基础建立一个局部域作为第3帧图像的扫描区域,以此迭代,直到寻找出所有图像的最优匹配图像;最后,记录下每张最优匹配图像的中心点坐标即可实现测量点的跟踪。采用改进的模板匹配定位方法得到的测量点跟踪效果图如图4所示。图中:红色矩形框内部的区域为局部域,蓝色矩形框内部的区域为最优匹配图像;绿圈点为跟踪的测量点。采用此方法处理1张图像所需的时间仅为0.1 s。


图4 测量点跟踪效果图
选取包含双受电弓通过被测吊弦的前20 s视频作为输入量,首先在第1帧图像中选取初始模板图像并定位初始测量点的位置,然后采用基于前1帧图像测量点位置的局部域匹配方法进行测量点的跟踪,最终可以提取出吊弦测量点的像素坐标。吊弦测量点以像素为单位的纵坐标-时间变化曲线如图5所示。
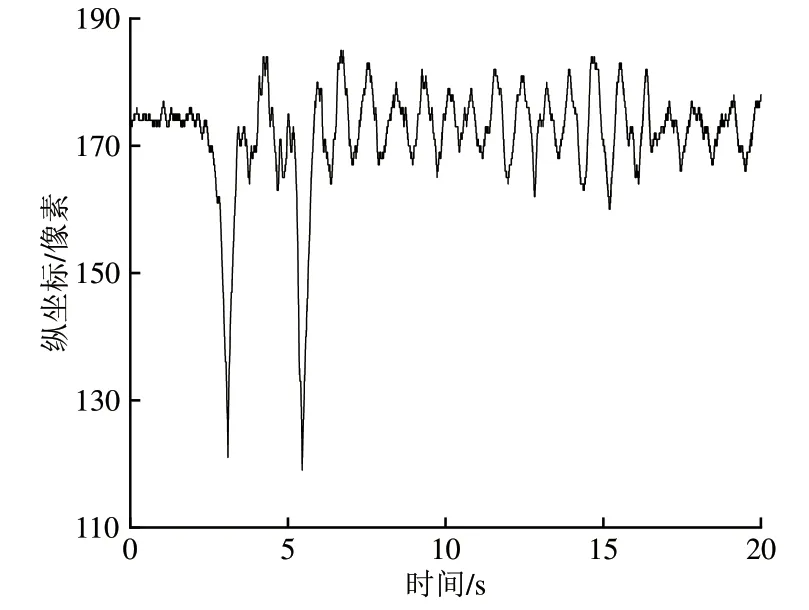
图5 吊弦测量点纵坐标-时间变化曲线
2 吊弦动态抬升量的测算
2.1 测量模型的建立
基于与模板图像的匹配,实现测量点的跟踪,可以获得测量点在像素坐标系下的空间位置。在此基础上,为进一步获得测量点在世界坐标系下的空间位置,基于相机小孔成像原理,建立吊弦抬升量测量模型如图6所示。图中:OWXWYWZW为世界坐标系;OCXCYCZC为摄像机坐标系;OC为高速摄像机的光心;O′XY为像平面坐标系;f为高速摄像机的焦距,即线段O′OC的长度;α为拍摄俯仰角;d为光心与测量点的水平距离;Pn为第n帧图像中的测量点;P′1和P′n分别为点P1和点Pn在像平面上的投影点;β1为线段OCPn距光轴的偏离角;β2为线段OCP1距光轴的偏离角;R和T分别为世界坐标系转换到摄像机坐标系的旋转矩阵、平移矩阵。

图6 吊弦抬升量测量模型
考虑吊弦横向的位移变化量几乎可以忽略不计,根据成像原理可知ΔP1PnOC和ΔP′1P′nOC始终共面,因共面切实存在线段P′1P′n始终与像平面的纵轴平行。因此,可以得到测量点实际位移变化量计算公式为
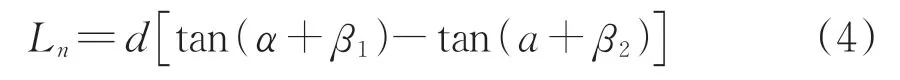
其中,

式中:Ln为第n帧图像测量点距第1 帧图像测量点间的实际位移变化量;y0为原点O′的纵坐标,通常取0;y1为点P′1的纵坐标;yn为点P′n的纵坐标。
2.2 摄像机参数标定和坐标系逆变换
式(4)中y1,yn和f都是未知的,为了求出像素坐标与实际位移之间的转换公式,需要对摄像机进行参数标定,并进行坐标系的逆变换,因此,引入世界坐标系、摄像机坐标系、图像坐标系、像素坐标系之间的转换关系。
世界坐标系可以通过旋转、平移等仿射变换转换为摄像机坐标系,这是一个从三维到三维的变换过程,如图6所示。一般都假定目标物体的测量点所在的平面经过世界坐标系的原点且与世界坐标系ZW轴垂直。可以通过下面的齐次坐标和矩阵关系式描述这一转换过程。

式中:(XCn,YCn,ZCn)为吊弦测量点Pn在摄像机坐标系下的坐标;(XWn,YWn,ZWn)为吊弦测量点Pn在世界坐标系下的坐标;K为世界坐标系转换到摄像机坐标系的外参矩阵。
摄像机坐标系可以经过投影变换转换为图像坐标系,转换过程如图7所示。该变换是一个三维到二维的变换过程,根据相似三角形可以得出吊弦测量点Pn在图像坐标系O′XY中的坐标(xn,yn)为


图7 摄像机坐标系与图像坐标系转换
图像坐标系O′XY与像素坐标系OUVUV都位于摄像机的成像平面上,这2 种坐标系只需经过尺度上的变换,再将各自的原点进行平移重合即可实现坐标系变换,变换过程如图8所示。图中:(u0,v0)为主点O′坐标,即图像的中心点在像素坐标系下的坐标。
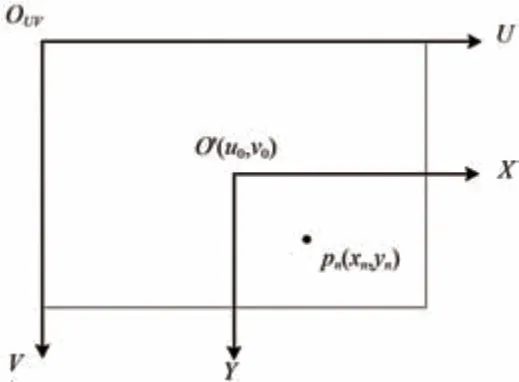
图8 图像坐标系与像素坐标系转换
通过式(7)可以实现2 种坐标系的坐标点之间的转换。

式中:dx和dy分别为单位像素在横向的实际长度和纵向的实际长度;(un,vn)为吊弦测量点Pn在像素坐标系OUVUV下的坐标。
综上,将式(5)、式(6)和式(7)整合可得到世界坐标系中坐标点到像素坐标系中坐标点的转换关系为

其中,
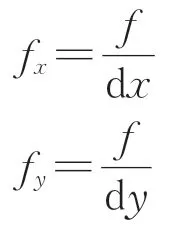
式中:M为内参矩阵;H为单应性矩阵。
根据式(8)可以发现,采用单应性矩阵H将世界坐标系下的坐标(XWn,YWn,ZWn)转换成了像素坐标系下的坐标(un,vn)。单应性矩阵由内参矩阵和外参矩阵的乘积组成。通过对单应性矩阵进行分解即可求解出内参矩阵,获得需要的内部参数。根据单应性矩阵8 自由度的性质[20]可以知道,只要获得4组世界坐标与像素坐标的匹配点对,就可以求解出唯一的单应性矩阵H,其中匹配点对的坐标都是已知的。基于张正友标定法[21],选取至少3张不同视角下拍摄的同一个标定物的图片,即可求解出摄像机的内部参数。
可以发现式(8)表示的是由世界坐标点转换为像素坐标点的1个正向过程,而对于吊弦动态抬升量的测量实际上是1个逆向的过程,即通过图像上已知的吊弦测量点的像素坐标(un,vn)和标定出的摄像机内部参数来求解吊弦测量点实际的空间坐标变化情况。最终,将求解的内部参数代入式(4)可得出吊弦测量点像素坐标与实际位移的转换关系式。

其中,
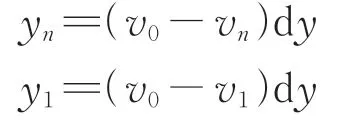
3 线路实测结果验证
3.1 吊弦动态抬升量实测结果
为了验证本文提出方法的有效性,在京广高速铁路武汉至乌龙泉东区间进行了实地拍摄,拍摄试验现场如图9所示。拍摄过程用到的设备名称、型号和用途见表1。

图9 试验现场

表1 设备名称、型号和用途
对高速摄像机进行内参标定,标定结果见表2。由于不方便在吊弦上进行靶标的安装,因此通过全站仪测量方式获取拍摄的距离和角度,其中:测量时高速摄像机光心到测量点的水平距离d=21 443 mm,拍摄的仰角α=18°22′13′。

表2 高速摄像机标定结果
由表2可知:内参fy的标定值与理论值的误差为5.25%;主点横坐标u0的标定值与理论值的误差为2.34%;主点纵坐标v0的标定值与理论值的误差为1.97%。该误差都在可接受范围内,因此标定的结果准确度较高。
拍摄过程中高速列车的运行速度为300 km·h-1,高速摄像机全程的拍摄帧率为2 000 帧·s-1。将高速摄像机拍摄的视频中包含双受电弓通过被测吊弦的前20 s进行处理,最终得到了吊弦动态抬升量时程变化曲线如图10所示。
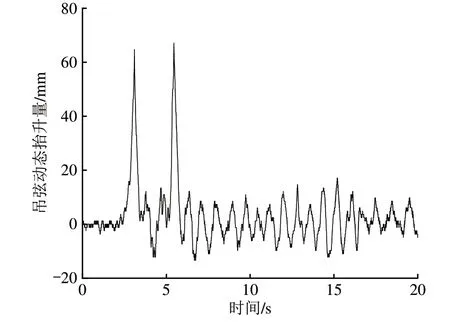
图10 吊弦动态抬升量时程变化曲线
3.2 实测结果的误差评估
通过分析图10 的测量结果,可以发现吊弦动态抬升量的幅值出现在前、后受电弓滑过测量点下方的时刻,这2 个时刻的抬升量也是测量的关注重点。以下对这2个时刻的测量结果做误差估计。
在式(9)中,吊弦动态抬升量的误差影响因素包括全站仪的测距精度、测角精度和图像识别的像素精度。该试验中全站仪的测距精度为±2 mm,测角精度为±2′,像素精度为±0.5像素。
基于误差理论对本文提出测量方法的理论误差进行评估。可以计算出前、后受电弓通过吊弦下端时的绝对误差Δy前=±3.0 mm,Δy后=±3.0 mm和相对误差δ前=±4.6%,δ后=±4.4%。前后弓滑过时的吊弦最大抬升量结果见表3。

表3 测量数据统计
由表3可知:前弓滑过时吊弦的最大动态抬升量为64.7 mm,会产生±3 mm 的误差量,该误差占最大抬升量的4.6%;后弓滑过时吊弦的最大动态抬升量为67.2 mm,会产生±3 mm 的误差量,该误差占最大抬升量的4.4%;产出的误差在可接受范围内。因此,本文提出方法的理论计算精度能够满足要求。
进一步分析测量精度对最终测量结果的影响,可以看出:整个理论误差中,测距误差和像素误差的占比为84.4%,测角误差的占比为15.6%。通过降低测量距离或改进测距精度、提高高速摄像机的拍摄画面分辨率,可以大大降低测量过程中产生的误差,提高吊弦动态抬升量测量结果的准确性。
4 结 语
本文提出了一种基于机器视觉的吊弦动态抬升量测量方法,可用于测量吊弦在接触线侧线夹的动态抬升量。基于鼠标交互的方式能够快速定位初始模板和初始测量点。基于二维离散余弦变换和哈希算法实现模板匹配,不仅能够实现测量点的跟踪,并能有效地提取出吊弦测量点的像素坐标,而且可以大大地提高图像处理速度。通过建立测量模型、标定摄像机内部参数并对坐标系进行逆变换求解,推导出了像素坐标与实际位移之间的转换公式。试验结果表明,本文方法能够快速有效地用于吊弦动态抬升量的定点实时测量,获得满足精度要求的结果,为研究弓网接触关系和吊弦的疲劳寿命提供实测数据支持。
