钢管混凝土桁架焊接T型管节点热点应力集中系数研究

卫 星，赵骏铭，肖 林，吴琛泰，温宗意

（1. 西南交通大学土木工程学院，四川成都 610031；2. 中国航天科工飞航技术研究院磁悬浮与电磁推进技术总体部，北京 100097）

钢管混凝土桁架造型美观，力学性能优良，广泛应用于大型拱桥的拱肋、钢-混组合桁架梁以及格构式桥墩上［1］。钢管混凝土桁架的主管（弦杆）和支管（腹杆）之间常以焊接管节点的形式实现连接。焊接管节点是将支管末端直接贴合地焊于主管表面而形成的空间相贯线焊缝接头。焊接管节点处的应力集中程度高，焊接引入的初始缺陷多，在车辆、风浪等荷载的反复作用下，管节点易发生疲劳破坏。

焊接管节点的疲劳评估宜采用热点应力法。焊接管节点的疲劳裂纹常发端于其焊趾处，热点应力即为该焊趾处的结构应力，它包含了结构几何不连续引起的应力集中，但不包括焊缝形状的影响。热点应力与结构的几何形式、尺寸、焊趾位置有关。热点应力集中系数（Stress Concentration Factor，SCF）为热点应力与名义应力之比，它相应地与管节点的无量纲几何参数有关，可表示为无量纲几何参数的函数（SCF 计算公式）。钢管混凝土桁架各杆件的名义应力可由桁架或梁理论求得，再将管节点无量纲几何参数代入SCF 计算公式，可以快速确定管节点的热点应力，从而提高热点应力法在焊接管节点疲劳设计中的应用效率。

国际管结构发展与研究委员会（CIDECT）［2］最早归纳整合了空心钢管桁架焊接管节点的SCF计算公式，该套公式为包括挪威船级社（DNV）［3］在内的等众多结构设计规范所认可和引用。而钢管混凝土桁架焊接管节点SCF 的计算目前尚未形成统一的公式见于设计规范或指南中。钢管混凝土桁架主管内填充的混凝土与钢管协同工作，管节点处的传力机理和变形模式必定和空心钢管有所不同，其SCF 亦需做额外研究。王柯［4］对钢管混凝土焊接T 型管节点进行了试验和有限元数值模拟，他将内填充混凝土等效为主管壁厚的增加，提出了等效壁厚的计算公式，并建议将等效主管壁厚代入空心钢管节点SCF 公式来计算与之对应的钢管混凝土管节点SCF。Xu 等［5］对T 型、K 型和KT 型管节点进行了静力试验，描述了SCF 沿管节点相贯线的分布。Zheng 等［6—7］、Musa 等［8-11］以及Tong等［12］均通过试验和有限元数值模拟，对T 型和K型管节点SCF 展开了参数研究，分别给出了各自研究得到的SCF 计算公式。吴琛泰［13］对钢管混凝土T/Y 型管节点SCF 进行了有限元参数分析，并探讨了主管轴向力引起的应力刚化效应对SCF 的影响。卫星等［14—15］研究了边界条件对Y 型管节点SCF 的影响，亦对钢管混凝土桁架板-管节点的SCF进行了相关研究。

综上，关于钢管混凝土管节点SCF 的研究有限，且大多仅关注了管节点典型位置（冠点和鞍点）处的SCF。由于管节点相贯线的几何复杂性，不同位置焊趾处的SCF 差别很大。考虑到疲劳裂纹发端位置具有很大不确定性，有必要对管节点上多个位置处的SCF 予以明确，对SCF 沿管节点相贯线的分布特征予以描绘。

运用有限元软件ANSYS 建立钢管混凝土桁架焊接T 型管节点有限元模型，进行支管轴向拉力作用下管节点热点应力集中系数研究，并基于有限元结果建立了钢管混凝土焊接T 型管节点SCF 最大值计算式。

1 有限元模型

T 型管节点几何结构如图1所示。图中：lc，dc和tc分别为主管的长度、直径和壁厚；lb，db和tb分别为支管的长度、直径和壁厚。管节点的无量纲几何参数主要包括长径比、管径比β=径厚比和壁厚比。有限元模型保证α大于10，以基本消除主管边界条件对SCF的影响［5］。参考部分国内已建成的钢管混凝土桁架拱桥焊接管节点设计参数，选定β的取值范围为0.3～0.7，γ为14.28～28.56，τ为0.4～0.8。

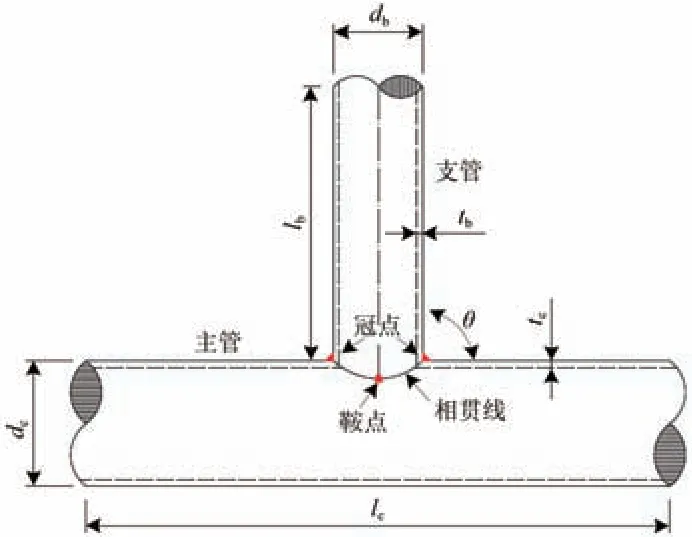
图1 T型管节点几何结构

管节点焊缝形状遵循美国焊接协会（AWS）的规定［16］，焊缝尺寸如图2所示。图中：tw为焊脚在主管上的投影长度。在冠点处，tw=0.4tb；鞍点处，在模型中将焊缝截面简化为相应尺寸的三角形。

图2 管节点焊缝几何尺寸

以支管轴向拉力为T 型管节点的疲劳激励荷载。主管两端采用固定铰支约束，以减少额外反力，实现对支管轴向力作用的单独研究。荷载与边界条件如图3所示。

图3 荷载与边界条件

图4为SCF测量点布置示意图。在支管轴线的法平面上建立如图4所示的极坐标系，φ为极角。由于本次模型的结构、荷载以及边界条件在0°和90°方向上均对称，所以仅需关注1/4 结构的力学行为。在0°～90°范围内，以15°为间隔设置7 个测量点，确定各点位的SCF，以描述SCF 沿管节点相贯线的分布。

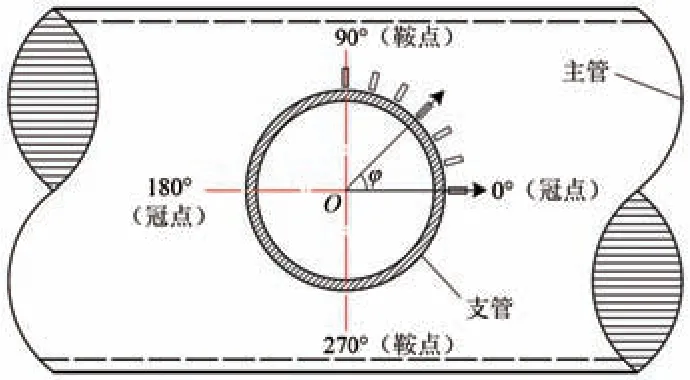
图4 SCF测量点布置示意图

采用ANSYS 建立圆钢管混凝土焊接T 型管节点有限元模型。模型主管全长范围内填充混凝土，支管仍为空心钢管。模型选用Q345 钢管和C50 混凝土，两者皆为钢管混凝土拱桥常用材料［17］。高周疲劳荷载作用下，可以仅考虑材料的线弹性特征，Q345 弹性模量为206 GPa，泊松比为0.3；C50弹性模量为34.5 GPa，泊松比为0.2［18］。

以实体单元SOLID45 和SOLID95 分别对模型的几何规则部分和复杂部分进行划分，如图5（a）所示。主管内壁和内填充混凝土表面的接触关系为面-面柔性接触。将接触单元CONTA173和目标单元TARGE170分别覆盖于主管内壁和混凝土核心的表面，组成接触对；钢-混界面的摩擦遵循库伦摩擦模型，取滑动摩擦系数为0.35［12］。模型主管内壁和混凝土表面的网格划分完全一致（图5（b）），保证了理想零初始间隙，使接触单元和目标单元一一对应，从而加快非线性运算的收敛。

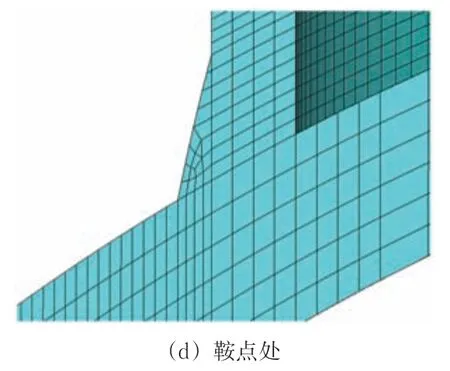
图5 有限元模型网格划分

通过有限元结果收敛性分析，发现当焊趾周围热点应力外推区的径向单元密度达到20 层、主管和支管壁厚方向分别划分为6 层和4 层单元时，热点应力计算结果收敛。冠点和鞍点处网格划分如图5（c）和图5（d）所示。

2 模型验证

采用T 型管节点模型（dc=914 mm，α=14，β=0.5，γ=14.28，τ=0.5，支管名义拉应力22.56 MPa）计算冠点处垂直于焊趾方向上的钢管表面应力分布，结果如图6所示。由图可知：正应力值基本等于第1主应力值，且愈靠近焊趾、数值愈大；临近焊趾处应力曲线变为平稳或下降，这是由焊趾处的几何不连续致使有限元结果出现奇异性造成的，因此，在有限元模型中亦需要使用外推法确定焊趾的热点应力。

图6 冠点处钢管表面应力分布

基于文献［12］的研究结论，结合本文有限元模型主管和支管热点应力外推区的应力分布特征，分别采用线性外推和2 次外推确定主管焊趾和支管焊趾处的热点应力σhs。采用国际焊接协会（IIW）［19］提出的有限元模型中热点应力外推计算公式，主管焊趾热点应力可由下式计算得到

式中：σ0.4c和σ1.0c分别为距离主管焊趾0.4tc和1.0tc位置处的主管表面垂直于焊趾方向的正应力。

支管焊趾热点应力可由下式计算得到

式中：σ0.4b，σ0.9b和σ1.4b分别为距离支管焊趾0.4tb，0.9tb和1.4tb位置处的支管表面垂直于焊趾方向的正应力。

参照CIDECT 管节点设计指南的规定［2］，焊接T型管节点在支管轴向力下的名义应力σnom为

式中：Fax为支管轴向力；A为支管截面积，对圆管有A=π(d21-d22) 4；d1和d2分别为支管的外径与内径。

SCF取值khs为

当结构处于线弹性状态时，khs与外荷载值无关，由结构本身的几何特征决定。

对文献［8］中2 个支管受拉的钢管混凝土焊接T 型管节点试件T-1 与T-3（图7）进行有限元数值模拟，试件尺寸与材料参数见表1。图8为SCF的试验结果与有限元计算结果。

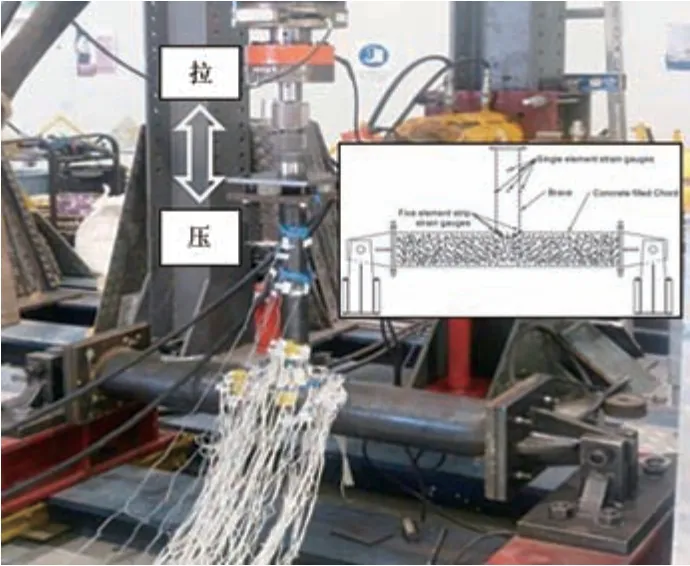
图7 文献［8］中的钢管混凝土管节点试件

表1 试件T-1与T-3结构尺寸与材料参数

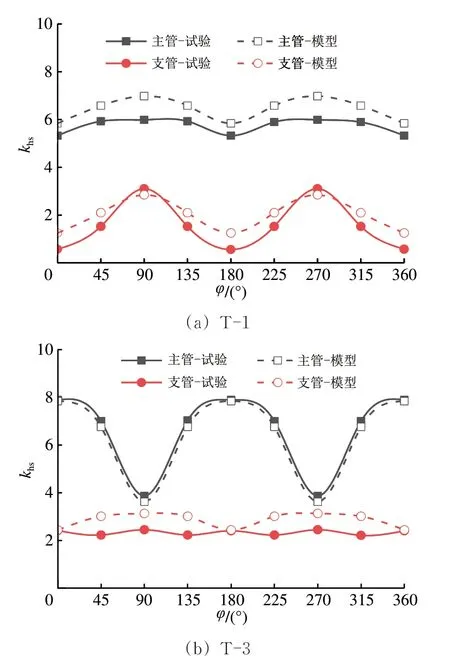
图8 SCF试验结果与有限元计算结果

由图8可知：T-1 主管和T-3 支管的有限元计算值略高于试验值，但总体上相差不大，且变化趋势基本一致。可以认为本文的有限元模型是可靠的。

3 T型管节点SCF研究

3.1 冠点与鞍点处的SCF

图9为冠点处SCF 随几何参数β，γ和τ的变化。由图9可知：主管冠点处SCF 与3 个几何参数均呈显著的正相关；与主管相比，支管冠点处SCF 整体水平较低，在2.0左右，且受几何参数影响较小，随其变化幅度基本在1.0以内。

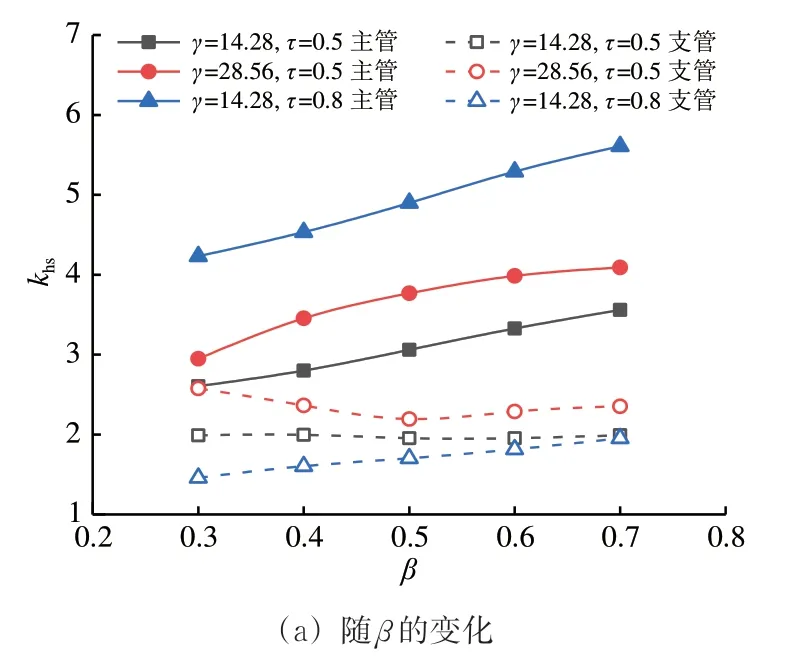
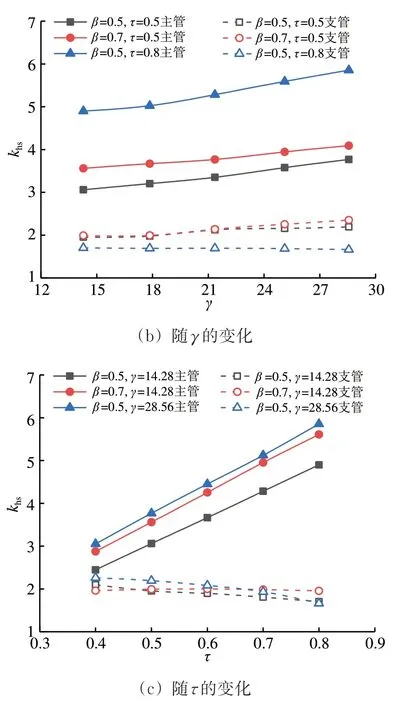
图9 冠点处SCF随几何参数的变化

图10 为鞍点处SCF 随几何参数的变化。由图10 可知：主管鞍点处SCF 与β呈负相关，与γ和τ呈正相关；支管鞍点处SCF随γ的增大而增大，随β和τ的变化幅度均较小，但当γ较大时，支管SCF随β增大而有较明显的下降。

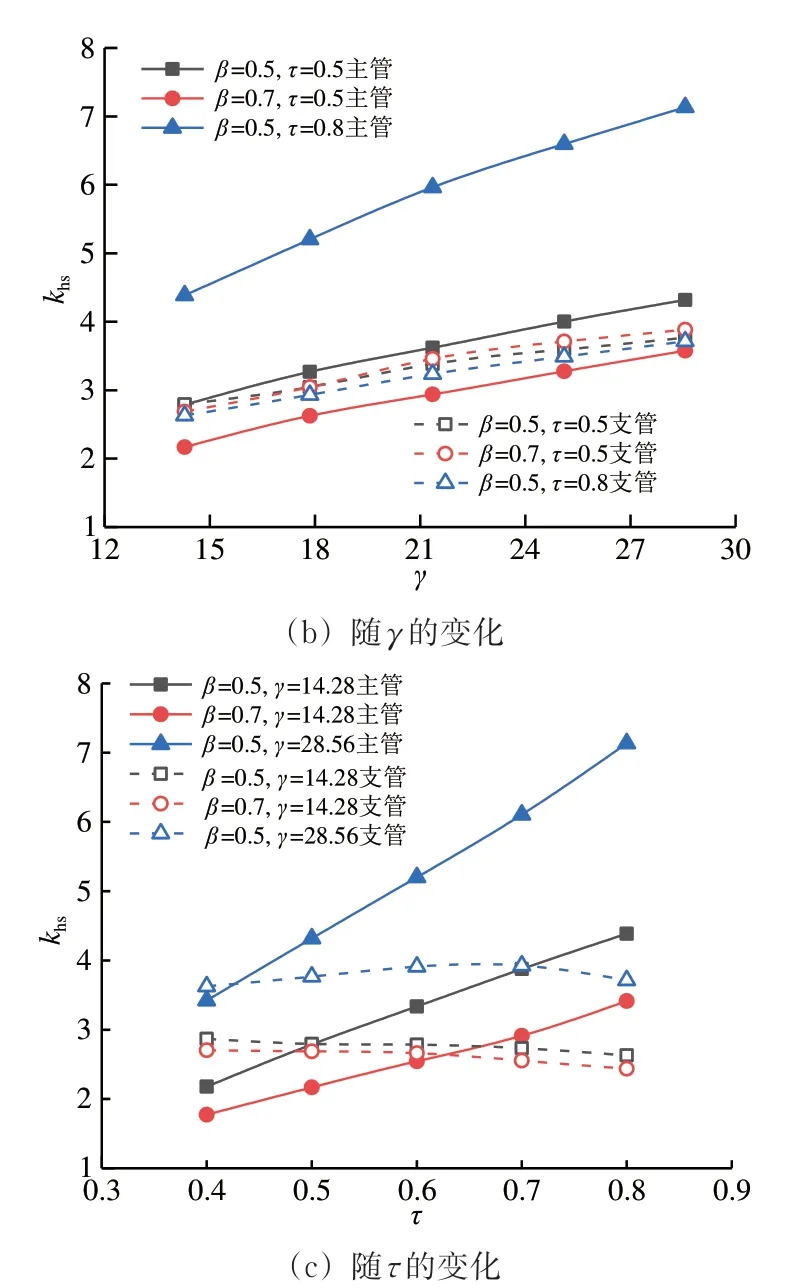
图10 鞍点处SCF随几何参数的变化

3.2 主管沿相贯线处的SCF

管节点相贯线焊缝主管侧的SCF 总体上高于支管侧的SCF，且在不同点位处主管侧SCF 之间的差距更大，所以着眼于主管SCF 沿管节点相贯线的分布。

主管SCF 沿管节点相贯线分布随几何参数变化如图11—图13所示。图中：横坐标φ为图4所示坐标系的极角。

由图11 可知：当β=0.3 时，冠点侧SCF 低于鞍点侧SCF，随着β的增大，冠点侧SCF 上升，鞍点侧SCF 下降，SCF 分布依次呈现出冠点侧与鞍点侧持平、冠点侧高于鞍点侧的模式。

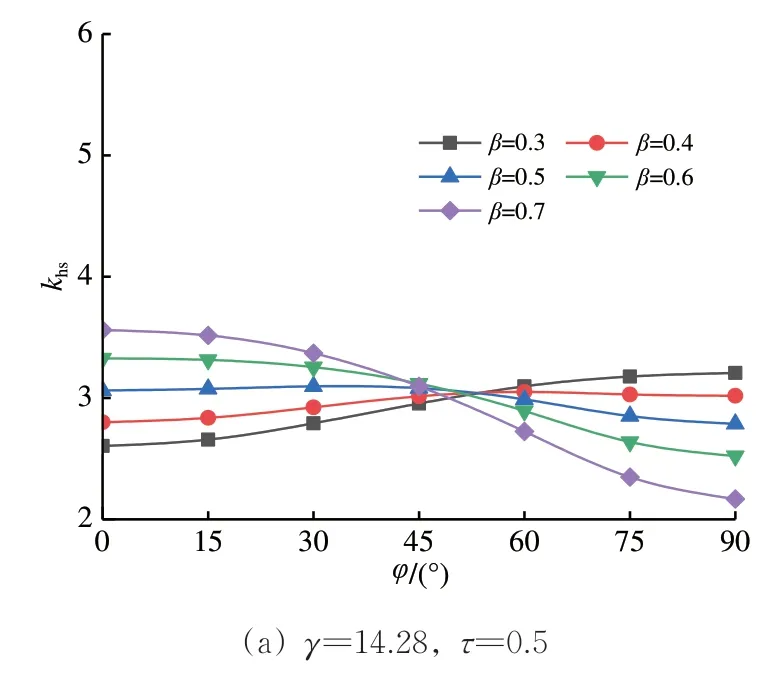
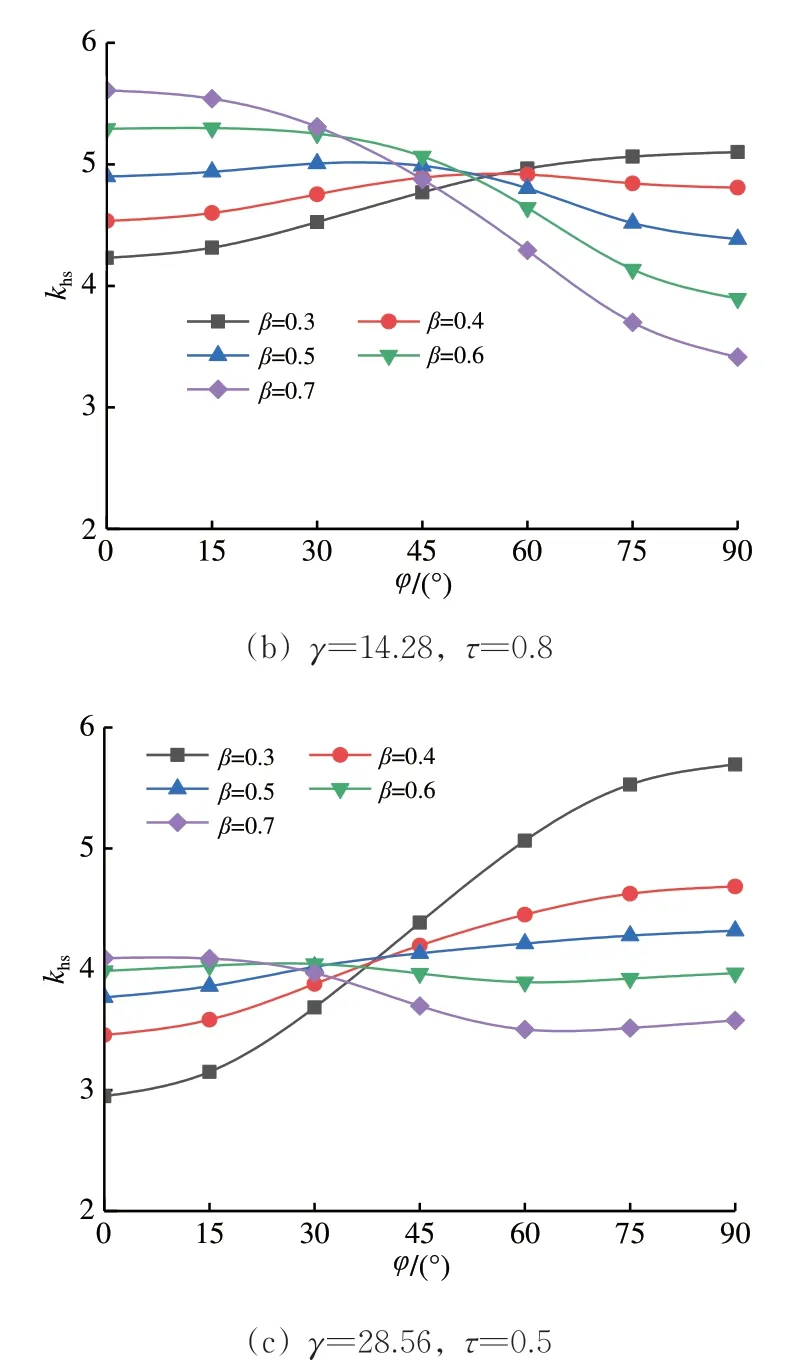
图11 主管SCF分布随β的变化

由图12 可知：当γ=14.28 时，鞍点侧SCF 低于冠点侧SCF；随着γ的增大，相贯线上所有位置处的SCF 均增大，但鞍点侧的增幅更大一些；当β为0.5 时，随着γ增大，鞍点侧SCF 逐渐超过冠点侧SCF 而成为最大值，但β为0.7时，冠点侧SCF整体上已高出鞍点侧SCF 许多，所以尽管鞍点侧SCF 增幅更大，但却始终未能超越冠点侧SCF。由此可见，管节点相贯线上各点位SCF 之间的相对大小受参数β和γ的共同影响。

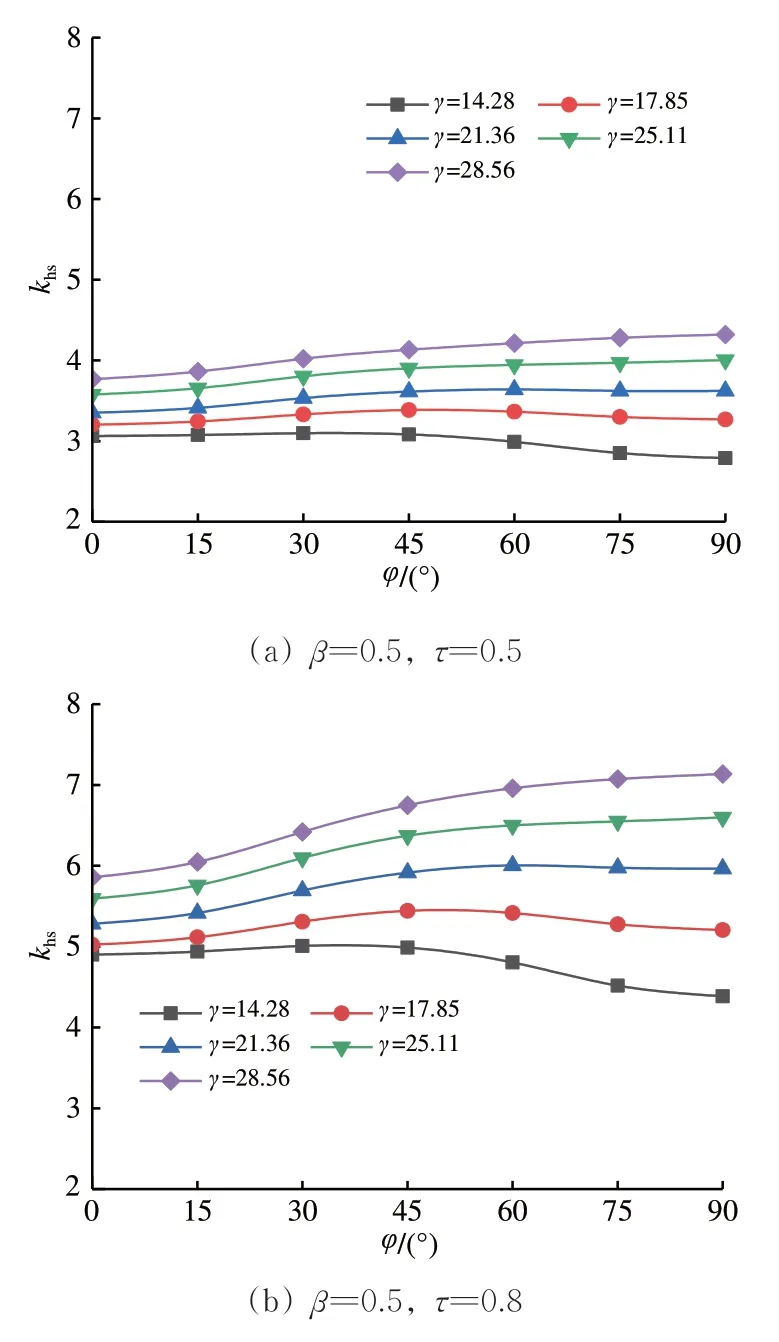
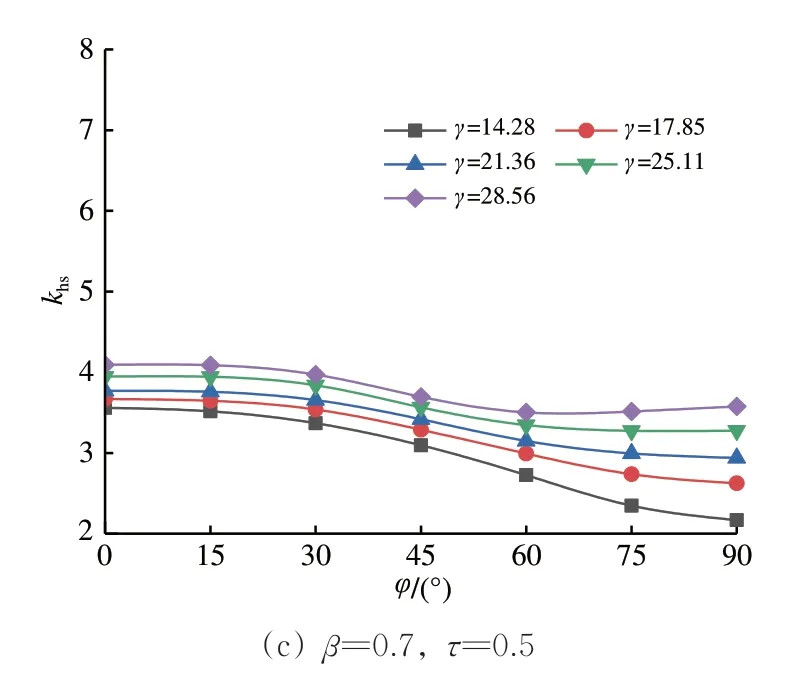
图12 主管SCF分布随γ的变化

由图13 可知：各点位的SCF 随τ的增大而均匀平稳上升，τ的增大仅提升主管SCF 的总体水平，而不改变各点位SCF的相对大小。

图13 主管SCF分布随τ的变化

3.3 SCF最大值

图14 为管节点相贯线焊缝SCF 最大值随几何参数的变化。由图14 可知：当γ为14.28 时，SCF最大值随β的增大先降低后升高，变化幅度较小，当γ增至28.56 时，SCF 最大值随β的增大而大幅度减小；SCF 最大值随γ的增大而增大，但β的增大会使该增速放缓；SCF 最大值与τ之间有较明显的正相关关系。

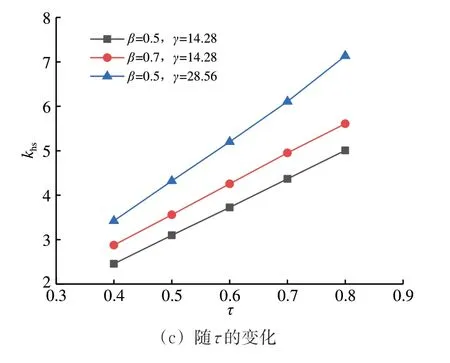
图14 SCF最大值随几何参数的变化

4 SCF最大值计算式

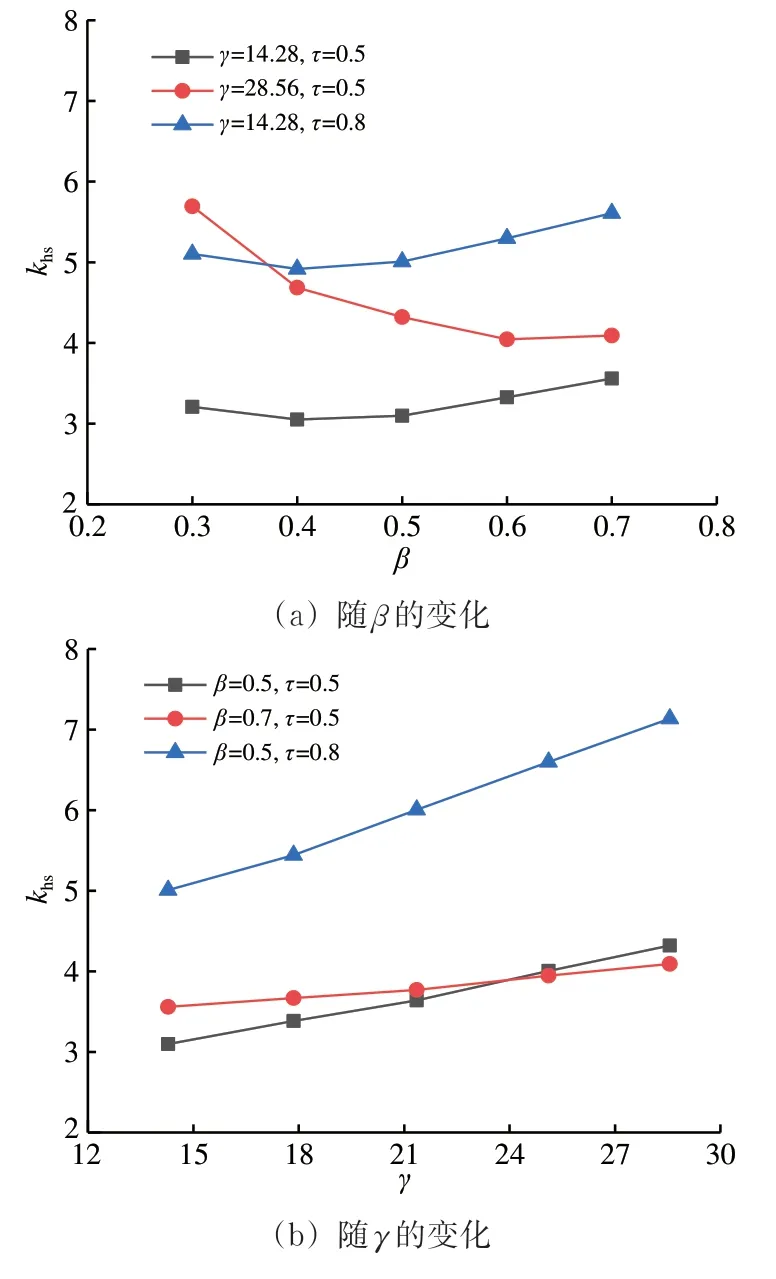
目前尚未有设计指南或规范明确给出钢管混凝土焊接管节点SCF的计算公式，仅有DNV［3］提出了主管内灌注水泥浆的钢管节点（灌浆钢管节点）SCF 计算方法。灌浆钢管节点与钢管混凝土管节点具有一定相似性，因此可采用DNV 计算式计算钢管混凝土管节点的SCF最大值。

根据DNV 计算式，T 型灌浆钢管节点鞍点和冠点处的SCF 分别由式（5）和式（6）求得，取二者的较大值作为管节点SCF最大值。

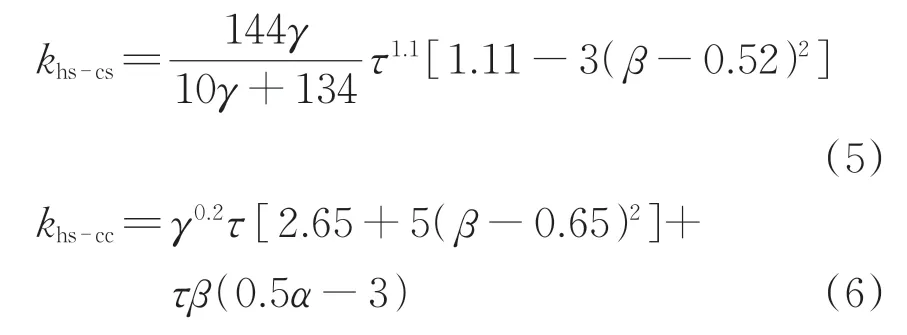
将有限元计算得到的SCF 最大值和DNV 计算式求得的最大值进行比较，如图15 所示。由图可知：DNV 计算式得到的SCF 最大值khs-max_eq与相应的有限元模型SCF 最大值khs-max_fe之比的平均值为1.157，变异系数为0.112，表明DNV 计算式略高估了钢管混凝土管节点的SCF。

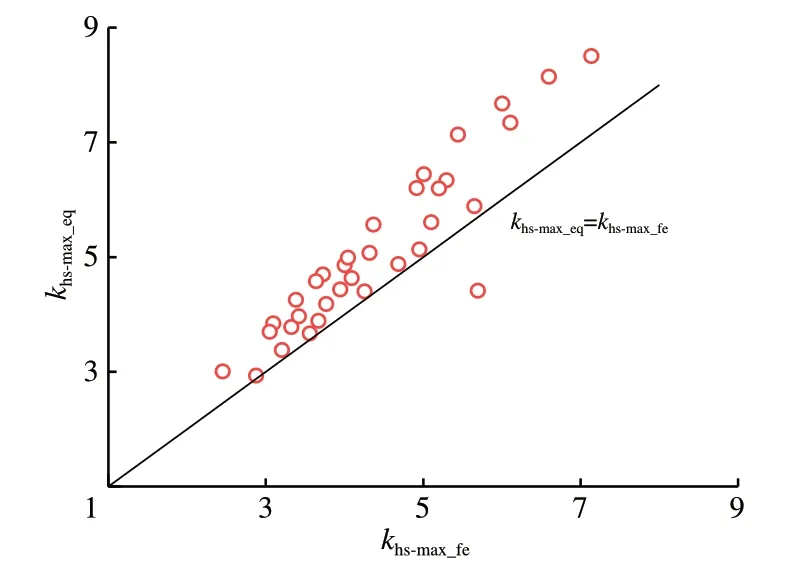
图15 DNV计算式结果和有限元模型结果的对比

基于本文有限元计算结果，通过多元非线性回归建立钢管混凝土焊接T 型管节点SCF 最大值khs-max的计算式。

式（7）的适用范围为：α＞10，0.3＜β＜0.7，14.28＜γ＜28.56，0.4＜τ＜0.8，基本涵盖了钢管混凝土桁架拱桥中管节点无量纲几何参数的取值范围。

本文计算式得到的SCF 最大值khs-max与相应的有限元模型SCF 最大值khs-max_fe之比的平均值为1.000，变异系数为0.020，计算精度高于DNV 计算式。表明本文计算式可合理预测一定几何参数范围内的T型管节点SCF最大值。

5 结 论

（1）主管冠点处SCF与参数β，γ和τ均呈正相关关系；主管鞍点处SCF 随γ和τ的增大而增大，但随β的增大而减小。与主管相比，支管冠点处SCF整体水平较低，随几何参数的变化幅度较小。

（2）就主管SCF 沿管节点相贯线的分布而言，τ使相贯线上各点位的SCF 均匀增减，从而不改变各点位SCF 的相对大小。当β较小时，各点位SCF 由冠点向鞍点逐渐上升；当β较大时，各点位SCF 由冠点向鞍点逐渐下降。γ的增大使各点位SCF 非均匀上升，越接近鞍点增幅越大，由此对SCF的分布产生影响。

（3）管节点SCF 最大值与γ，τ成正相关。当γ较小时，β的增大使SCF 最大值先下降后升高，但变化幅度不大；当γ较大时，SCF 最大值随β的增大而显著减小。

（4）DNV 提出的灌浆钢管节点SCF 计算公式高估了钢管混凝土管节点的SCF 值。基于本文有限元计算结果，提出了钢管混凝土焊接T 型管节点的SCF最大值计算式。