高铁线路轨道高低不平顺激励下的钢轨挠曲特性研究

牛留斌，刘金朝，肖炳环，徐晓迪

（中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081）

轨道的高平顺性是车辆安全运行的前提，轨下基础良好的支承性能是保持轨道空间形位的关键。线路上不可避免的轨道不平顺是引起轮轨振动的主要激励源，其波长和幅值是决定轮轨振动频率和烈度的主要因素。轨道不平顺对车辆的影响特征与不平顺波长有关，如短波轨道不平顺引起轮轨高频振动和环境噪声，长波轨道不平顺引起车体低频振动［1］，特别是引起车辆振动频率接近其固有频率1 Hz 左右的波长被定义为敏感波长［2］。轨道不平顺引起轮轨间附加动态力对轨道的影响不低于静轮重［3］。过大的钢轨动态位移会加速轨道结构累积变形不利于保持轨道几何空间形位，不但增加运营线路的养护维修工作量，还可能会引发轨道局部结构破坏，增大车辆运行风险。垂向动载荷作用下钢轨挠曲变形是轨下基础服役状态的综合体现，钢轨挠曲位移为线路的质量评价、维修管理等提供了参考依据，如我国新建线路验收规范［4］中规定了钢轨垂向位移的最大允许值和基准值；国外采用高频数字相机［5］、位移传感器［6］等技术手段测量关注区的钢轨动态位移，根据其变化特征分析轨下基础支承的劣化状态。

钢轨挠曲位移除了与其承受的垂向载荷有关外，还受到轨道垂向位移导纳特性［7］、轨下基础刚度及车辆运行速度等因素影响，是一个复杂的车辆-轨道-基础系统动力学问题。Chen Y H 等［8］利用匀速运动坐标系下无限长铁木辛柯（Timoshen⁃ko）梁与欧拉-伯努利（Bernouli-Euler）梁在黏弹性地基上引起的钢轨计算位移差异；Basu D 等［9］基于温克尔（Winkler）弹性地基无限长连续Ber⁃nouli-Euler梁理论的稳态响应解析解，研究移动载荷速度对钢轨挠曲位移的影响。除了理论解析求解稳态钢轨挠曲位移外，数值仿真技术也应用于轨道基础变化时钢轨挠曲求解中。如Giannakos 等［10］建立路基-道床-轨枕-钢轨模型研究无砟线路上因轨道板出现裂纹时引起轨道整体刚度劣化规律及钢轨挠曲位移突变特征，理论结果在现场测试中得到了验证；Chung W 等［11］建立的有限元模型中将轨道板连结方式等效为剪切弹簧，研究了移动载荷作用下浮置板轨道的挠度特征；Auersch 等［12］采用轮轨耦合动力学理论建模，研究了不同频段的道床、支承刚度不平顺对钢轨垂向振动加速度、钢轨挠曲位移等时频域变化特点的影响；Kacimi A E等［13］建立三维轨道-车辆有限元模型，数值模拟了高速列车单车通过钢轨时轮轨间复杂的振动响应，以及列车通过速度对轨道动态挠曲的影响；Ang K K 等［14］利用移动单元分析方法建立非均匀黏弹性地基三维多刚体列车模型，研究了移动荷载在速度和轨道不平顺的组合工况下轨道刚度突变恶化导致轮跳现象，以及轮跳时动力放大系数和车体加速度变化情况；Shan Y 等［15］采用多体力学和有限元相结合的方法构建单自由度模型，研究了25 m·s-1速度条件下低频轨道几何不平顺激励钢轨挠度及车体垂向加速度变化特性；宋小林等［16］通过车辆-轨道耦合动力学模型，仿真计算高速条件下的动态轮轨力作为输入条件时，板式无砟轨道钢轨垂向位移在时空频域上的分布情况。以上研究中，较多关注了固定载荷或者实测动态载荷作用下求解钢轨挠曲变化特性，而将轨道设置成理想平顺状态，轨道不平顺激励的轮轨力折算成固定频率的简谐函数［17］，将其引起的挠曲位移耦合在钢轨总挠曲位移之中。开展轨道高低不平顺激励的钢轨挠曲位移变化规律的研究，有利于为我国高铁线路重点关注波长的精准选择，为完善轨道不平顺的波长管理提供科学依据。

本文基于我国典型高铁线路及服役车辆主要参数，建立车辆-轨道耦合动力学仿真模型，在模型中输入我国高铁无砟轨道谱反演的轨道高低不平顺，研究速度350 km·h-1条件下轨道不平顺幅值和波长对钢轨挠曲位移在时域和频域上的变化特征，利用非线性最小二乘法［18］拟合幅值和波长引起的钢轨挠曲最大值之间的函数表达式；结合研究结果及中国高速铁路无砟轨道谱曲线，给出高铁波长管理建议。

1 模型建立

车辆运行过程中，钢轨在轮轨垂向力作用下产生弹性挠曲变形，轨道静态不平顺发展成轨道动态不平顺，轮轨垂向力FP可分解为静轮重和动态附加力2部分［17］，即

式中：FP0为静轮重，kN；FPdyn为动态附加轮轨垂向力，kN。

与FP0和FPdyn对应，钢轨的总位移y由2 部分构成，即

式中：ys和yd分别为静轮重FP0和动态附加力FPdyn引起的钢轨挠曲位移，mm。

构建轮轨耦合动力学模型研究yd与轨道静态高低不平顺之间的关联特性，耦合模型由车辆子模型和轨道结构子模型组成，如图1所示。图中：M和Mb分别为车体和转向架的质量；J和Jb分别为车体和转向架点头转动惯量；z，zbi（i=1，2）及zwj（j=1，2，3，4）分别为车体、前后转向架及4 个轮对垂向沉浮位移；θ和θbi分别为车体和前后转向架的俯仰角；Pj为轮轨接触力；k1，c1，k2及c2分别为车辆一系、二系悬挂刚度和阻尼；L为转向架中心到车体中心的距离；Lb为同一转向架上2 个轮对轴距的一半；ks和cs分别为钢轨支承扣件系统的等效刚度和阻尼；kH为轮轨接触刚度。

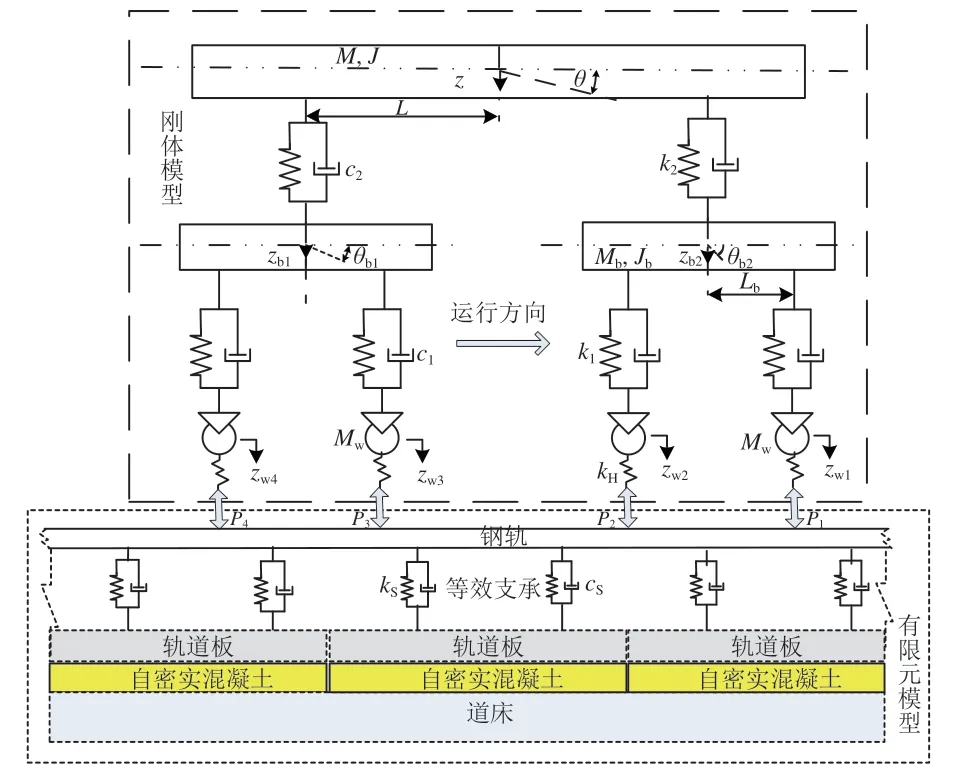
图1 轮轨耦合动力学模型示意图

1.1 车辆子模型

车辆刚体模型选用CRH380A 型动车组参数建模，包括1 个车体、2 个构架及4 个轮对，车辆一系、二系悬挂系统用弹簧阻尼元件模拟。钢轨挠曲位移主要与垂向激励有关，车辆子模型中包含了车体俯仰角θ，前后构架俯仰角θbi，车体沉浮位移z，前后构架沉浮位移zbi及4 个轮对沉浮位移zwj等共计10个自由度。车辆子模型的动力学方程为

其中，

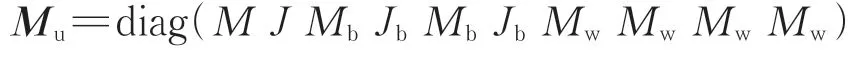
式中：Mu，Cu及Ku分别为车辆子模型的质量、阻尼及刚度矩阵；uu和P分别为车辆子模型的位移向量和载荷向量；g为重力加速度。

1.2 轨道子模型

轨道子模型包括钢轨、轨道板及混凝土底座等部件，采用CRTS Ⅲ型轨道结构和CN60廓形钢轨参数建模，有限元网格均采用三维实体单元进行精细化建模，扣件系统等效为支承弹簧，建立轨道结构子模型简图如图2所示。

图2 轨道结构子模型

轨道结构子模型的动力学方程可表示为

其中，

Pr=(Pr1Pr2Pr3Pr4)

式中：Mr，Cr，Kr及ur分别为轨道结构子模型质量矩阵、阻尼矩阵、刚度矩阵及位移矩阵；Pr为轮轨接触位置钢轨受到的轮轨接触力。

车辆子模型与轨道结构子模型通过式（3）和式（4）中轮轨接触力相联系，在轮轨接触位置，车辆与轨道受到的轮轨力是1 对相互作用力，即Prj=-Pj。采用Newmark-β 法显式求解振动方程式（3），得到车辆子模型位移向量uu；采用Abaqus 软件和轨道子模型仿真得到式（4）中的位移向量ur。轮轨接触力Pj由Hertz 非线性弹性接触理论［19］得到，即

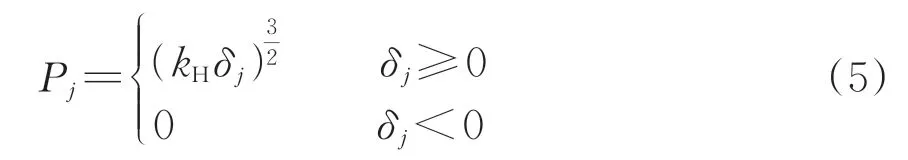
式中：δj为采用罚函数法计算轮轨接触点间的相对位移。

某时刻轮对j穿透钢轨表面的距离为δj，轮轨接触示意图如图3所示。

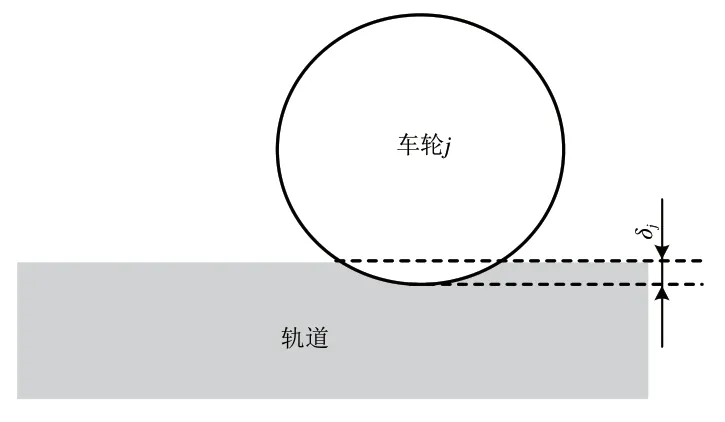
图3 轮轨接触示意图

采用修改钢轨横断面上全部网格节点坐标的方式在轨道模型上施加轨道高低不平顺，如图4所示。图中，钢轨网格节点A处的轨道不平顺幅值为dzA时，将原节点坐标A(xA，yA，zA)修正为新的节点坐标A’(XA’，YA’，ZA’)，换算式为

图4 轮轨动力学轨道模型网格调整示意图

式中：θ1为轨道坡角度；h为CN60 廓形钢轨高度，176 mm。

1.3 轮轨耦合动力学模型

钢轨挠曲位移及轨下基础频响范围主要集中在0～40 Hz［20］，速度350 km·h-1条件下对应的轨道不平顺波长大于2.4 m，因此主要研究波长在1.5～120.0 m 范围内的轨道静态高低不平顺引起的钢轨挠曲变化特性（如不特殊说明，下文模型中输入的轨道高低不平顺均为轨道静态高低不平顺）。轨道高低不平顺采用我国高速铁路无砟轨道谱反演样本和余弦型模拟波形。余弦型高低不平顺作为输入时，计算区域包含10个完整周期的波形。我国高速铁路无砟轨道高低不平顺谱计算式［21］为

式中：f为空间频率，m-1；Sv(f)为轨道高低不平顺谱，mm2·m；ψ和B均为分段拟合系数，rad·m-1。

式（7）中拟合系数见表1。

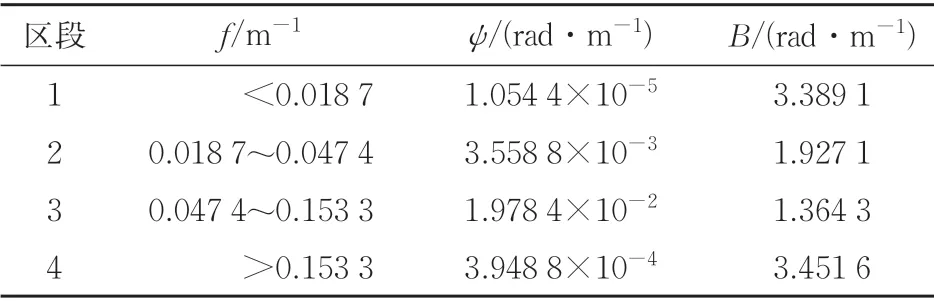
表1 轨道高低不平顺谱拟合系数

综上，轮轨耦合动力学模型的数据处理步骤如下。

（1）建立轨道结构子模型，施加位移边界条件，并在钢轨上设置轨道高低不平顺。

（2）运用Abaqus 软件隐式模块计算重力作用下位移场，得到轮轨耦合动力学模型初始时刻t0时的位移向量。

（3）在t1时刻，由式（5）求出轨道不平顺条件下的轮轨垂向力向量Pj，时间步长为10-5s。

（4）采用Newmark-β法和式（3），计算车辆子模型在轨道不平顺条件下的位移向量uu，1。

（5）利用MATLAB 修改inp 文件中轮轨接触力位置参数，并提取轮轨接触处节点的位移ur，1。

（6）由uu，1，ur，1和式（5）计算得到轮轨垂向力向量Pru，1，重复上述步骤（4）和（5），得到uu，2和ur，2；如果计算结果满足式（8），则uu，2，ur，2及prw，2为t1时刻车辆轨道振动位移和接触力的结果；如果不满足式（8），则继续上述步骤（4）—步骤（6），直到前后2次计算结果满足式（8）。

式中：ε为极小数，取10-6。

（7）重复上述步骤（3）—步骤（6），计算t2，t3，…，结束时刻tend车辆、轮对、轨道等位移和轮轨接触力结果。

（8）依次输出钢轨上所有节点的挠曲位移，统计该工况下的钢轨挠曲位移等变化规律。

（9）修改步骤（1）中钢轨节点坐标，仿真计算新轨道高低不平顺工况下的钢轨挠曲位移曲线。

（10）汇总各计算工况下钢轨挠曲位移曲线，提取波形曲线时频域特征，进行趋势拟合等分析处理。

本文所建轮轨耦合动力学模型的仿真参数见表2和表3。

表2 车辆子模型主要参数

表3 轨道子模型主要参数

2 模型验证

轨道结构的振动频段较低，支承弹簧等部件的阻尼对钢轨挠曲位移影响较小［22］。基于Winkler弹性地基理论，钢轨在轮轨垂向力FP作用下挠曲位移yz0解析式［9，23］为其中，

式中：z0为轮轨接触位置纵坐标，mm；k为轨下基础刚度，N·m-1；β为钢轨的刚比系数；E为钢轨材料的弹性模量；J0为钢轨截面惯性矩。

通过叠加式（9）的单轮结果，得到多轮对作用下的钢轨挠曲位移ys为

式中：I为轮对个数；当z-zI大于5 m 时轮对之间挠曲影响非常小，我国车辆同一转向架轮对间轴距小于3 m，式（10）中轮对个数n取2。

通过放大静态挠曲位移，得到移动载荷作用下钢轨挠曲位移yd为

式中：αv为速度放大系数，在车辆运行速度为350 km·h-1时α350取值1.5［24］。

车辆以速度350 km·h-1通过未施加高低不平顺的轨道时，钢轨挠曲波形如图5所示。由图5可以看出：因扣件的不连续支承作用引起钢轨挠曲位移在静轮重FP0引起的ys附近周期性波动，波动幅度为0.005 mm，波动的长度等于支承弹簧的间距。

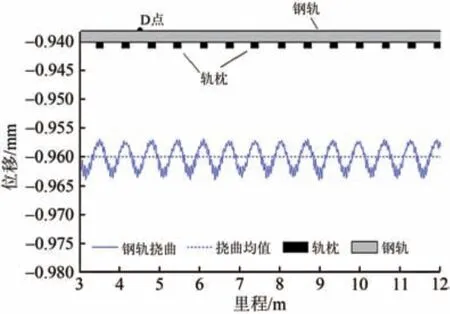
图5 未施加轨道高低不平顺时钢轨挠曲位移图

图5中钢轨某点D垂向挠曲位移时程曲线及由式（11）计算得到的解析解对比如图6所示。

图6 钢轨挠曲位移理论与仿真计算结果

由图6可以看出：前轮对接近D点时，同一转向架前后轮对引起的钢轨挠曲位移分量逐渐增大并叠加在一起；前轮在D1时刻到达D点，此时钢轨挠曲位移的最大挠度值为-0.76 mm；前轮对通过D点后，前轮对引起的钢轨挠曲位移逐步减小，后轮对接近D点，引起的钢轨挠曲位移在逐步增大，在D2时刻前轮对远离D点而减小的挠曲位移量分量与后轮对靠近D点而增大的挠曲位移分量相等，此时钢轨挠曲位移为-0.66 mm；后轮引起的钢轨挠曲分量逐步增大，在D3时刻后轮对到达D点时，钢轨挠曲位移达到最大值为-0.96 mm；此后，后轮对远离D点，前后轮对引起的钢轨挠曲位移分量均逐渐减小，直至D4时刻钢轨D点近似回到平衡位置；图1轮轨耦合动力学模型输出的钢轨挠曲位移仿真结果与理论解析解变化趋势一致，波形吻合良好。

在钢轨上施加波长1.5 m 幅值1 mm 轨道高低不平顺时仿真得到的轮轨垂向力变化曲线，与文献［25］在相同参数下的仿真结果进行对比，如图7所示。

图7 轮轨垂向力仿真波形与文献结果对比

由图7可以看出：2 种仿真计算得到的轮轨垂向力波形吻合较好，峰值相近，验证了模型仿真结果的正确性；0～20 m 里程内是未施加轨道高低不平顺区段，该区段轮轨垂向力的小幅度波动是由扣件不连续支承引起的。

图6中钢轨挠曲位移随低通截止频率的变化曲线如图8所示。由图8可以看出：在截止频率为500 Hz 时，钢轨挠曲位移趋于的稳定值。因此，输出结果滤波均采用500 Hz低通滤波。

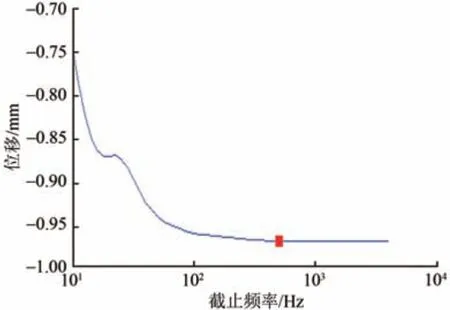
图8 钢轨垂向位移随截止频率变化曲线

3 数值计算结果

我国高铁无砟轨道谱反演得到的轨道高低不平顺样本如图9所示。

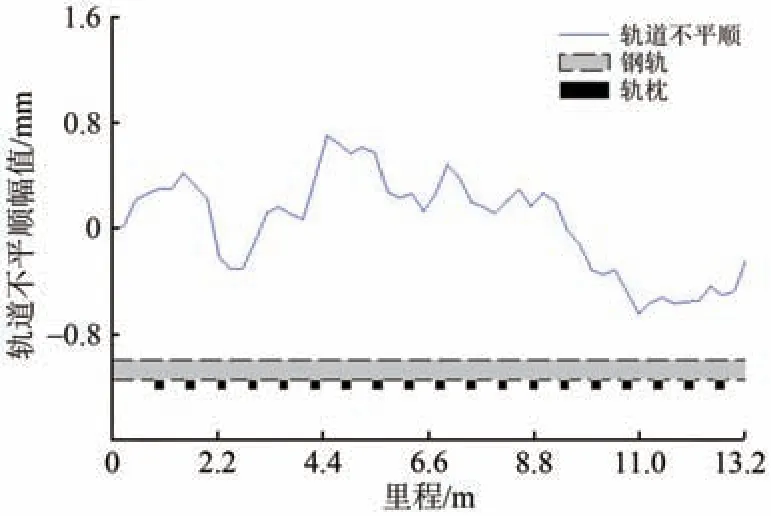
图9 轨道高低不平顺样本

为了研究不同幅值轨道高低不平顺激励下钢轨挠曲位移变化规律，对其幅值进行放大，放大系数AMF（Amplitude Multiple Factor） 取2，4，5，8。利用式（6）在钢轨模型中输入轨道高低不平顺样本，轮轨垂向力及采用不同放大系数进行幅值放大后的钢轨挠曲位移曲线仿真结果分别如图10 和图11所示。

图10 不同AMF下轮轨垂向力波形曲线

由图10 和图11 可以看出：随着AMF的增大，钢轨挠曲位移yd的变化趋势相似，即相位未发生变化，但波动范围在逐步增大；AMF为8 时，部分轮轨垂向力为0，说明轮轨间出现脱离，但对钢轨挠曲位移极大值影响较小。

图11 不同AMF下钢轨挠曲位移曲线

不同放大系数AMF条件下挠曲位移与AMF=1时的挠曲位移之差反映了幅值变化量对钢轨挠曲位移的影响，定义幅值增大倍数AIF（Amplitude In⁃crease Factor）的值为AMF-1，不同AIF下的钢轨挠曲变化曲线如图12所示。

图12 不同AIF下钢轨挠曲位移增量

钢轨挠曲位移曲线波谷位置对应的纵坐标值为钢轨挠曲变化量，采用AIF=7 钢轨挠曲位移曲线2阶导数为正值的方法得到12 组曲线波谷位置，如图中圈选位置所示。过曲线波谷位置做平行于纵坐标轴的点状竖线，依次定义线1、线2、…、线11。每条线与钢轨挠曲位移曲线的交点，自上而下依次为AIF=1，AIF=3，AIF=4，AIF=7 时的钢轨挠曲位置局部最小值，统计线1—线11上波谷位置对应的纵坐标值，结果见表4。由表4可知：每条线上4个交点（波谷）处对应挠曲位移值的比例关系约为1∶3∶4∶7，与AIF值在对应位置取值的比例关系基本一致。这说明随着轨道高低不平顺幅值增大，钢轨挠曲位移yd的波形和相位不变，幅值与其最大值近似成正比。

表4 图12中钢轨挠曲位移局部小值mm

因此，波长为λ、幅值为Aλ的轨道高低不平顺引起的钢轨挠曲位移yd(Aλ，λ)可记为

波长λ=1.5 m、幅值Aλ=1 mm 余弦型轨道高低不平顺条件下钢轨轮轨垂向力、挠曲位移仿真结果如图13所示。

图13 幅值为1 mm、波长为1.5 m轨道高低不平顺时模型仿真结果

由图13 可以看出：在轨道高低不平顺激励下轮轨垂向力呈现余弦型变化特征，两者周期一致，而钢轨在轮轨垂向力作用下的yd呈现有规律的波动，不再具有单频率正余弦变化特征，其频谱曲线如图14所示。

图14 yd频谱曲线及谐波成分波形

由图14 可以看出：yd频谱曲线中包含多个等间隔峰值，yd是由多阶周期性谐波成分叠加而成的，基频为0.666 7 m-1，对应的空间波长为1.5 m；4 阶以上谐波的峰值与基频峰值之比小于10%，1～4次谐波成分所占比重较大。

因此，幅值为1 mm、波长为λ的轨道高低不平顺引起的yd(1，λ，z)的函数方程可用前4 阶傅里叶级数展开式表示为

式中：α0为静轮重FP0为引起的钢轨挠曲位移，mm；ak，βk分别为k阶谐波成分振幅、谐波与轨道高低不平顺之间延迟相位；ωλ为轨道高低不平顺激励角频率，

由式（13）可知，yd的各谐波分量的振幅a与波长λ有关，波长λ分别为1.5，2，3及4 m条件下的轮轨垂向力如图15 所示。由图15 可知：不同波长条件下的轮轨垂向力在静轮重FP0附近波动范围依次为±40.9，±22.2，±9.6和±5.5 kN，呈现出轮轨垂向力随着波长λ增大而减小的趋势。

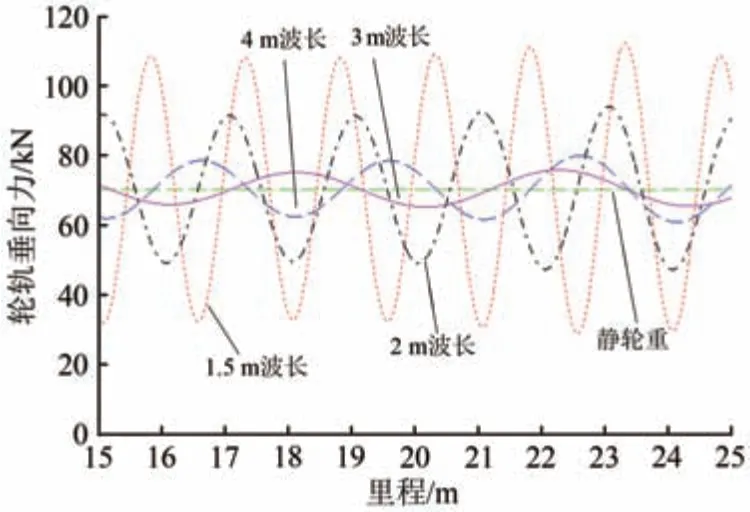
图15 不同波长条件下轮轨垂向力

轮轨垂向力引起的各谐波分量振幅a与其频率有关，轨道结构子模型中钢轨垂向导纳位移特性曲线如图16所示。图中：速度350 km·h-1条件1.5～120.0 m 波长的轨道高低不平顺激励角频率为0.8～65.0 Hz，远离共振频率［26］frail且不存在共振突变峰曲线，如深色区域所示。

图16 钢轨垂向导纳位移曲线

由图16可以看出：随着轨道高低不平顺波长λ增大其引起的激励角频率变小，1 kN 的轮轨垂向力引起的钢轨垂向挠曲位移减小。

由以上分析可知，随着波长λ的增大和轨道高低不平顺激励的轮轨垂向力减小，轮轨垂向力频率也变小，引起的钢轨垂向挠曲位移变小。将式（13）中yd(1，λ，z)的最大值记为α(λ)，即α(λ)=max(yd(1，λ，z))，波长λ在1.5～12.0 m、幅值1 mm 时钢轨挠曲位移最大值α由0.38 mm 下降到0.02 mm，如图17所示。

图17 钢轨挠曲位移最大值

在轮轨耦合动力学模型中输入波长λ为1.5～120.0 m 幅值1 mm 的轨道高低不平顺，仿真计算对应的钢轨挠曲位移α(λ)，并采用非线性最小二乘法［18］对波长λ与α(λ)之间进行拟合，方程为

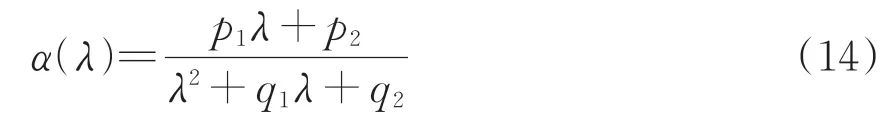
式中：p1，p2，q1及q2均为待定拟合系数。

在拟合优度大于99.5%时，α(λ)与波长λ之间的拟合曲线及系数如图18所示。

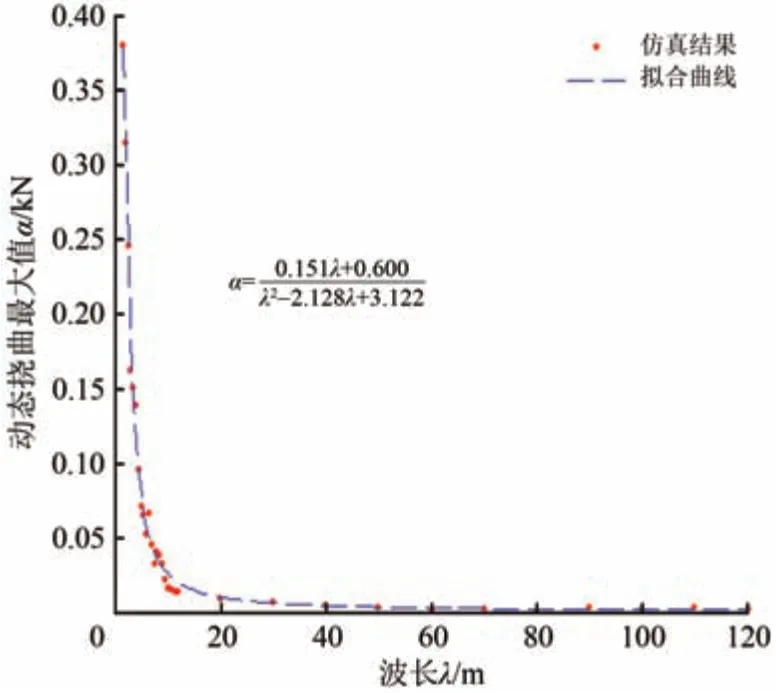
图18 钢轨挠曲最大值随波长变化散点及拟合曲线

由式（2）和式（14）可知，波长λ幅值Aλ的轨道高低不平顺激励下钢轨最大挠曲位移ymax的计算式为

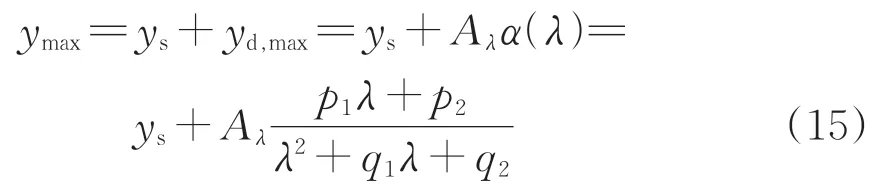
当波长λ大于20 m 时，式（15）中的值较小，可简化为

式中：比例系数p1取0.151（见图18）。

由式（16）可知，轨道高低不平顺幅值Aλ与波长λ比值近似与钢轨挠曲位移最大值成正比。

现行的轨道高低不平顺局部峰值［24，27］管理模式未能充分兼顾波长对线路的动态影响，利用式（15）可以从轨道动态挠曲位移控制的角度维护线路，精准找出轨道管理重点关注的波长范围。某速度350 km·h-1高铁线路轨道高低不平顺实测波形，其幅值处于±2 mm 之间，对其进行傅立叶变换，再按式（16）得到的钢轨最大挠曲位移曲线yd，max，结果如图19所示。

由图19 可以看出：该线路的轨道高低不平顺中20～35 m 波长成分的幅值较大，而波长在1.5～10.0 m 范围内的轨道高低不平顺成分能够引起较大的钢轨挠曲位移。

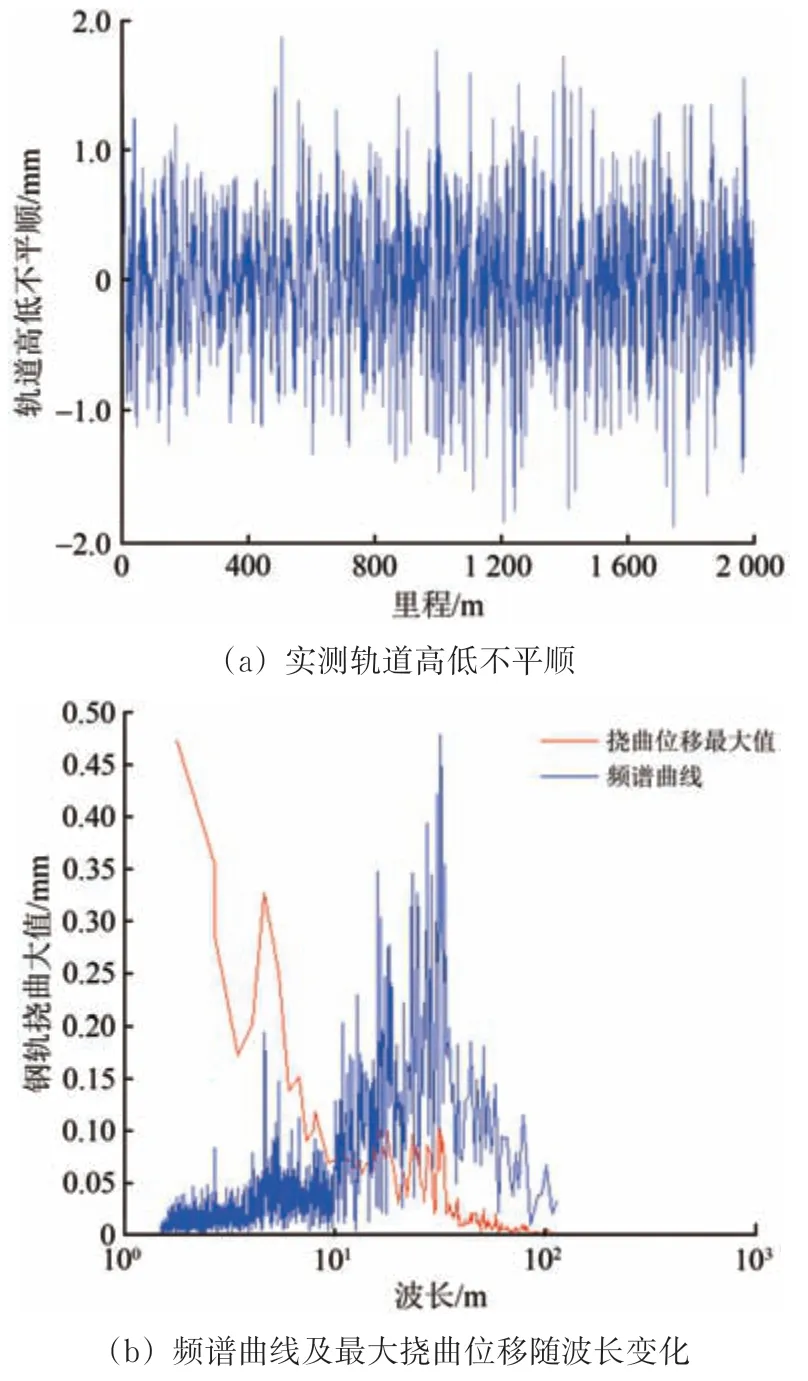
图19 某线路实测轨道高低不平顺数据

4 结 论

（1）构建轮轨耦合动力学模型研究速度350 km·h-1条件下轨道高低不平顺引起的钢轨挠曲位移特性，通过对比钢轨挠曲位移仿真结果与理论解析的方式解验证了模型输出的准确性。我国高铁无砟线路轨道谱反演的高低不平顺样本数据仿真结果表明：轨道高低不平顺的幅值不影响钢轨动态挠曲位移yd响应特征且yd的变化量与轨道高低不平顺的幅值变化量近似成正比。

（2）钢轨垂向位移导纳特性随着波长在1.5～120.0 m 范围内的高低不平顺激励频率增大而增大。随波长的增大轨道高低不平顺激励的轮轨垂向力值及其频率均减小，而钢轨挠曲位移随着垂向力值及激励频率减小而减小，并由轨道高低不平顺引起的多次谐波叠加而成，基波频率是由波长和车辆运行速度决定，4 阶及以上谐波成分所占比重小于10%。

（3）利用非线性最小二乘法及有理式方程拟合了速度350 km·h-1条件下钢轨挠曲位移与轨道高低不平顺幅值、波长之间关系曲线。在波长大于20 m 时，幅值与波长比值近似和最大钢轨挠曲位移量成正比，比例系数为0.151。