频变特性下自耦变压器绕组FRA建模研究

周利军，周祥宇，林 桐，吴振宇，高仕斌，张陈擎宇

（西南交通大学电气工程学院，四川成都 611756）

自耦变压器绕组采用具有较强抗冲击能力的分裂式绕组结构，主要应用于高速铁路动车组供电［1］。由于高铁运行环境复杂，受雷击过电压、输电线路短路等影响可能会产生短路大电流，可能造成自耦变压器绕组变形、移位等故障，不断的故障累积最终将对自耦变压器造成不可逆损坏［2-3］，及时有效的绕组状态检测具有重要意义。而实际的自耦变压器，由于造价昂贵，难以进行绕组故障模拟探究故障下频率响应变化特征。因此，通过搭建具有相同绕组结构的自耦变压器绕组故障模拟实验平台，采用实验与仿真相结合的方法，研究故障下绕组频率响应变化规律是必要的。

频率响应分析（Frequency Response Analysis，FRA）法是目前检测变压器绕组故障的主要手段，适用于绕组结构相同的大型自耦变压器绕组建模。频率响应法的工作原理是：在绕组1端注入扫频信号（1～1 000 kHz），另1端接受输出响应，然后通过计算获得扫频下的绕组幅频特性曲线［4］，横向或纵向对比绕组频率响应特征，识别绕组状态。变压器绕组可以等效为由电阻（R）、电感（L）、电容（C）参数构成的无源网络，故障下绕组电气参数的改变是导致频率响应变化的主要因素［5］。针对绕组频率响应建模，国内外的学者进行了大量研究。周利军等［6］针对牵引变压器绕组进行了状态空间方程建模，提出1 种考虑全电容、电感参数模型，并验证了模型的有效性。刘思伟等［7］通过有限元获得绕组故障下电气参数变化规律，基于集总参数电路模型获得绕组频率响应特征频带随故障程度变化的规律，最后通过现场实验验证其研究成果可有效应用于实际变压器绕组故障检测。HASH⁃EMNIA N 等［8-9］建立了绕组集总参数电路模型，获得绕组轴向移位与径向变形下电气参数变化与频率响应的映射关系；NOSRATIAN AHOUR J等［10］提出1种绕组改进型集总参数梯级网络模型，通过仿真和实验对比验证了该模型能够较好地反映绕组频率响应的反谐振点；SHINTEMIROV A等［11］提出1 种适用于高、低频的绕组混合多导体传输线模型，分析了高频下频率响应的变化规律，可用于识别绕组轻微变形。但上述建模方法并未考虑高频下电感和电阻参数的改变对于频率响应模型的影响，而由于频率响应测试频带较宽，高频下变压器铁心受涡流效应影响发生去磁效应，绕组的电感参数会发生改变，且高频下绕组受集肤效应影响电阻参数也会发生改变。

本文通过考虑变压器铁心与绕组的频变特性，针对1台含梯级叠铁心自耦变压器分裂式绕组进行频率响应建模研究。首先利用数值计算及均质化建模，获得不同方向的叠铁心各向异性相对有效磁导率的频变特性；然后通过有限元仿真获得绕组电感和电阻的频变特性；再在MATLAB 中建立频变特性下绕组的状态空间方程，通过解析模型获得正常及轴向移位下绕组的频率响应；最后通过实验验证模型的正确性。

1 频变特性下绕组电气参数计算

建立频变特性下自耦变压器绕组的频率响应模型，首先要获得绕组电气参数的变化规律。通过分析变压器铁心导磁特性的频变规律，均质化建模获得铁心的相对有效磁导率；然后利用有限元软件静磁场计算绕组电感在1～1 000 kHz的变化规律，利用有限元软件涡流场计算绕组电阻在1～1 000 kHz的变化规律。

1.1 铁心的相对有效磁导率计算

首先在有限元仿真软件Maxwell中利用涡流场对变压器硅钢片建模，仿真得到不同频率下硅钢片磁通密度分布，如图1所示。由图1可知：当频率在1 kHz 以上时，硅钢片受涡流效应的影响靠近边界的磁通密度最大；在涡流场中计算得到，随着频率的增大硅钢片的平均磁通密约由1.0 T 减小至0.1 T，说明硅钢片的去磁效应影响不容忽略。

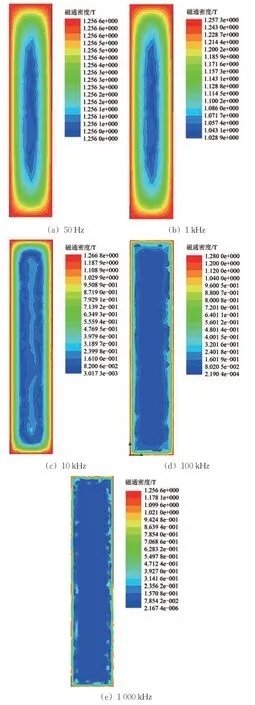
图1 不同频率下硅钢片磁通密度分布

单层硅钢片交变磁场中的各向异性如图2所示。图中：x，y和z为空间的3 个矢量方向；Bx，By和Bz分别为3 个方向下的磁通密度；Jx，Jy和Jz分别为3个方向下的电流密度。根据硅钢片导磁原理，单层的硅钢片处于1个交变的磁场空间中，磁通密度可以等效为3 个不同方向的磁通密度构成其中“∧”表示复数形式；不同方向的磁通密度均为矢量。硅钢片具有一定的导电率，因其处于交变的磁场中，由法拉第电磁感应定律可知，在硅钢片x，y和z方向产生涡流

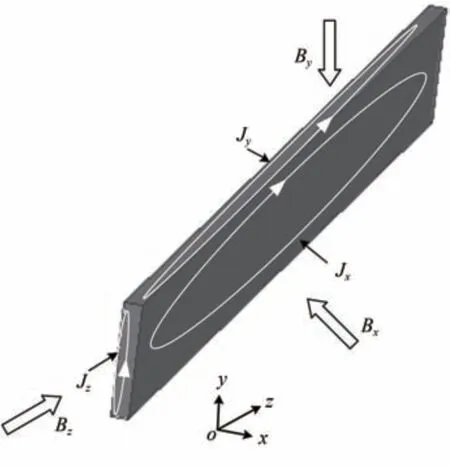
图2 单层硅钢片交变磁场中的各向异性

为了分析高频下涡流效应对于硅钢片导磁性能的影响，将硅钢片非线性导磁特性B-H曲线线性化得到硅钢片各向异性磁导率。硅钢片导磁特性及导电特性可以表示为［12］

式中：B为磁通密度，T；μ为不同磁通密度下硅钢片的磁导率；H为磁场强度，A·m-1；J为电流密度，A·m-2；σ为硅钢片的电导率，S·m-1；E为电场强度，N·C-1。

硅钢片导磁特性的各向异性可以表示为［13］

式中：μxx，μyy和μzz分别为硅钢片在x，y和z方向工频下的相对有效磁导率，其值可根据文献［14］的均值化磁导率计算式获得。

根据文献［15］有效磁导率频变特性的经典计算式，硅钢片不同方向下相对有效磁导率与频率的关系式为

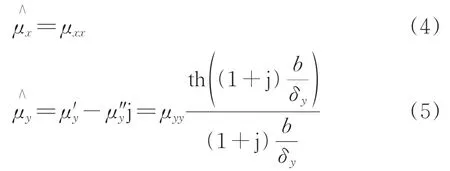
其中，

式中：μx，μy和μz分别为x，y和z方向不同频率下的相对有效磁导率；μ'y和μ″y分别为y方向不同频率下μy的实部和虚部值；th(·)为双曲正切函数；b为单层硅钢片的厚度，m；δy和δz分别为y和z方向的集肤深度，m；μ'z和μ″z分别为z方向不同频率下μz的实部和虚部值；w为磁通密度的角频率，rad·s-1；μ0为真空磁导率。

变压器铁心是由数量较多的硅钢片在x方向压叠制成的，如图3所示。传统的变压器铁心模型由无梯级硅钢片压叠制成，如图3（a）所示；实际的变压器铁心多由含有梯级的硅钢片压叠制成，如图3（b）所示。为了减少涡流损耗，单层硅钢片均涂有绝缘层。

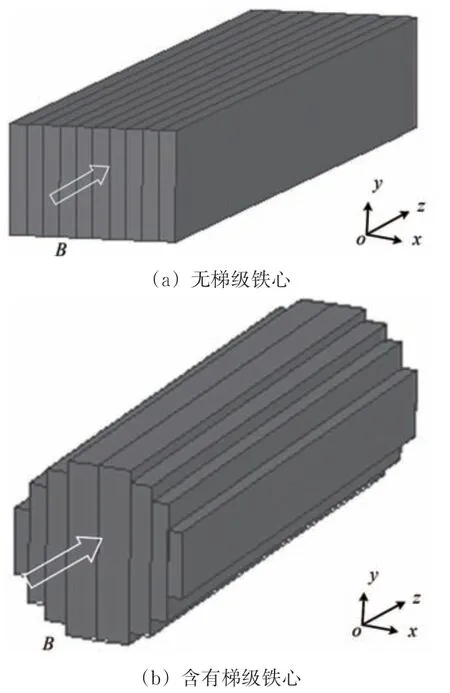
图3 变压器叠铁心示意图

设铁心的叠片系数为α，则无梯级铁心在x方向的相对有效磁导率μxr计算式［16］为

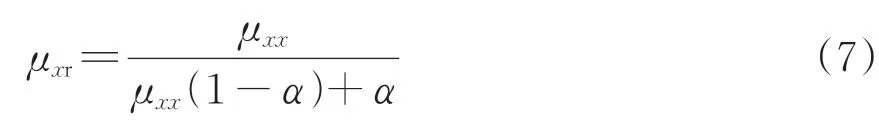
对于含有梯级铁心的变压器，在有限元建模中以单层硅钢片为基础建模不现实，需要对其进行均质化建模。根据文献［17］，含有梯级铁心叠层硅钢片和均质化模型之间的磁阻等效计算式为

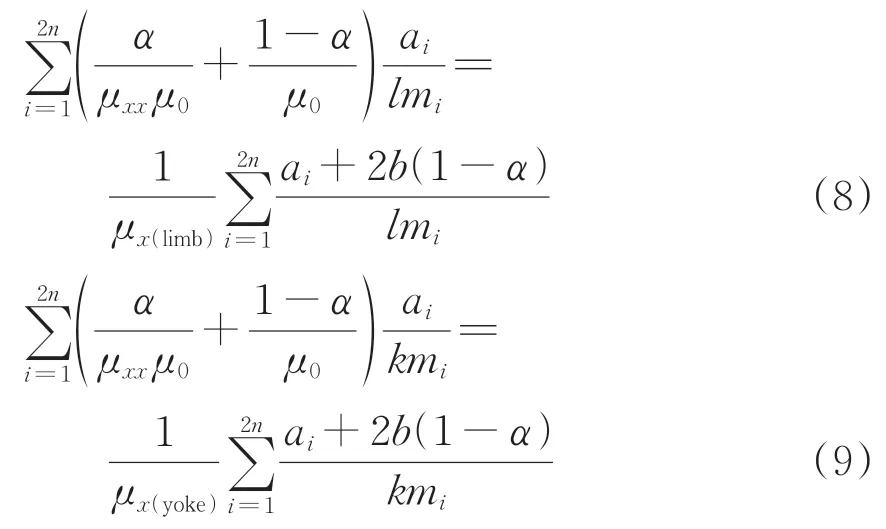
式中：μx（limb）为铁心心柱均质化后的有效磁导率；μx（yoke）为铁心铁厄均质化后的有效磁导率；n为含梯级铁心的梯级数量，级；ai为不同梯级的厚度，m；mi为铁心心柱不同梯级下截面宽度，m；l为铁心心柱的长度，m；k为铁厄顺磁方向长度，m。

由式（7）和式（8）可知，均质化模型铁心心柱及铁厄的有效磁导率相等，即μx（limb）=μx（yoke）。由此可得铁心心柱和铁厄的相对有效磁导率计算式为

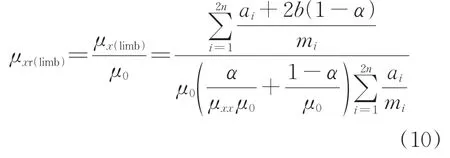
在y和z方向，由于磁通不会穿越硅钢片的绝缘层，仅沿着单层硅钢片导磁，因此不需要考虑绝缘层对于铁心导磁性能的影响。根据文献［17］可知，铁心均质化模型在y和z方向的相对有效磁导率仅与铁心的叠片系数相关，分别为

本文的研究对象是1 台10 kV/50 kVA 的自耦变压器，其铁心由分梯级的硅钢片压叠制成，硅钢片型号为武汉宝钢生产的B30P120。根据厂家提供的硅钢片B-μ曲线，计算获得硅钢片在3 个方向工频下的相对有效磁导率分别为μxx=μyy=24.92，μzz=426.00。变压器的基本参数见表1，将铁心参数带入式（5）和式（6），计算获得变压器铁心y和z方向下的相对有效磁导率频变特性，如图4所示。图中：Uzz和Uyy分别表示铁心在z和y方向的相对有效磁导率。由图4可知，随着频率增大，铁心相对有效磁导率逐渐减小。

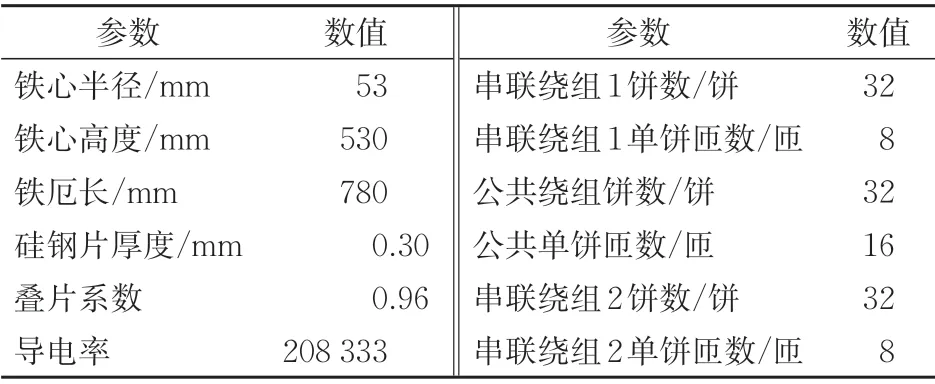
表1 变压器基本参数值

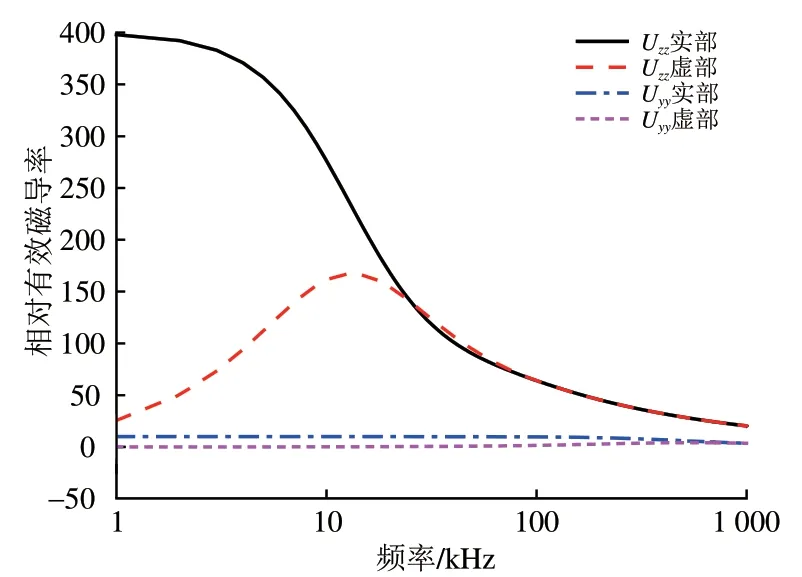
图4 变压器铁心相对有效磁导率的频变特性

1.2 频变下绕组电感计算

根据获得的不同频率下铁心相对有效磁导率，在Ansoft Maxwell软件中建立叠铁心自耦变压器绕组三维有限元模型，如图5所示。在有限元模型中设置铁心材料各向异性，在静磁场求解器计算获得不同相对有效磁导率下电感。

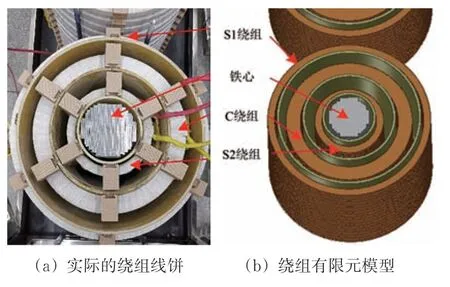
图5 自耦变压器绕组及三维有限元模型

由于变压器绕组电感与所加激励无关，只和变压器铁心导磁性能、绕组材料以及匝数、尺寸相关，本文设置变压器绕组激励源是1 A 电流源，利用静磁场能量原理计算不同绕组的电感以及绕组之间互感。其中，1个饼单元产生的磁场能量Wm为

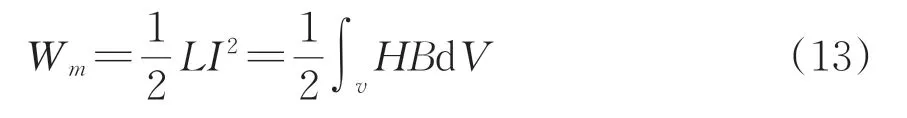
式中：L为导体电感，mH；I为绕组输入电流，A；v为单饼绕组几何空间。

由式（13）推导出以饼为单元的导体电感L为

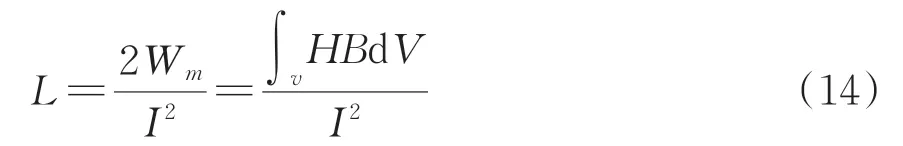
针对考虑梯级和未考虑梯级2 种情况，在有限元软件中计算不同频率时绕组的电感，以绕组第1饼线圈为例，绕组电感的频变特性如图6所示。由图6可知：随着磁导率的逐渐减小，绕组电感是逐渐减小的；扫频频率从1 kHz 增大至1 000 kHz 时不同位置绕组电感变化不一致，C 绕组的电感由1.5 mH减小至0.8 mH，减小约46.7%，S1绕组的电感由0.47 mH减小至0.26 mH，减小约44.68%，S2 绕组的电感由0.35 mH 减小至0.16 mH，减小约54.28%；考虑铁心梯级影响后的电感比未考虑铁心梯级影响时在数值上更为偏大，而根据电力行业标准DL/T 911—2004［18］知，频率响应在中频段的谐振点对于电感的变化具有较高灵敏性，因此对含梯级叠铁心均质化建模是有必要的。

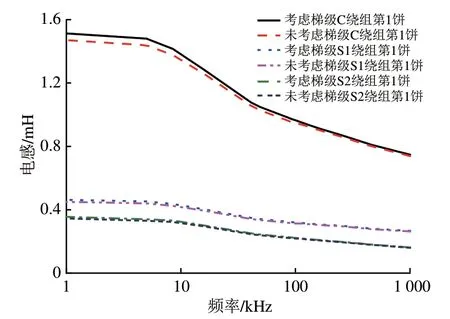
图6 不同位置绕组的电感频变特性

1.3 频变下绕组电阻的计算

10 kHz下绕组导体内电流分布如图7所示。由图7可知：电流主要分布在导线的表面以及拐角处，这是由于高频下导体邻近效应和集肤效应的影响。在频率响应建模中以饼为单元绕组的电阻R在大于1 kHz 时必然会发生改变，在有限元涡流场计算获得绕组电阻频变特性［8-9］，如图8所示。由图8可知：随着频率增大，绕组电阻逐渐增大，C 绕组导体电阻在1 000 kHz时变化最大，约为0.55 Ω，S2绕组在1 000 kHz时变化最小，约为0.10 Ω。

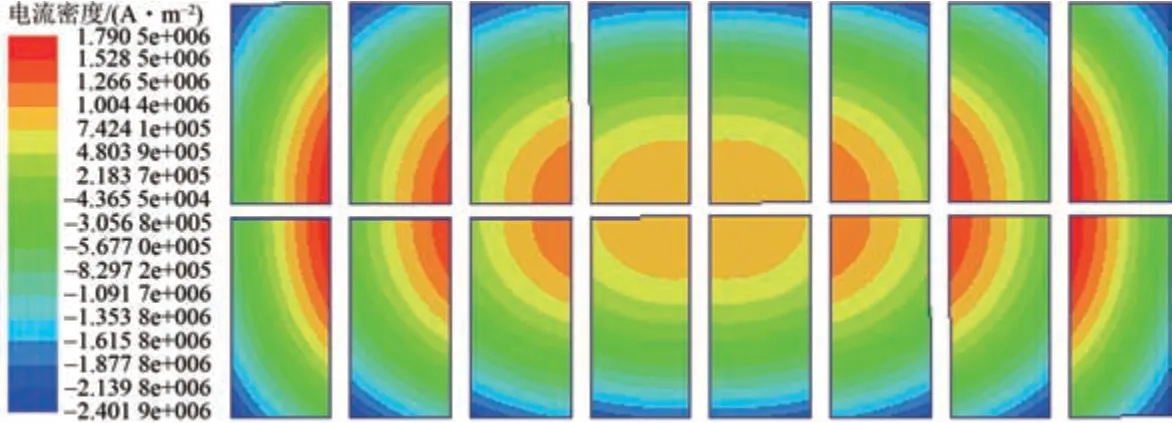
图7 10 kHz下绕组导体内电流分布

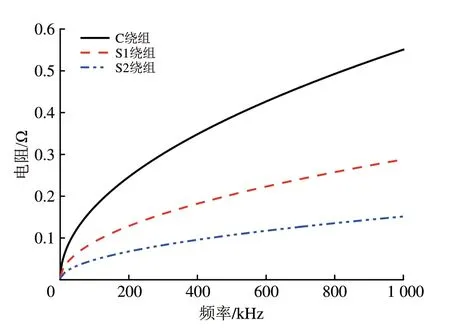
图8 不同位置绕组的电阻频变特性

2 解析模型构建与验证

2.1 频变特性下绕组频率响应建模

在PSPice/EMTP 中搭建传统集总参数电路模型获得的频率响应，绕组的电感及电阻是固定不变的，无法反映电气参数的频变特性。因此，基于集总参数电路模型，以饼为单元建立绕组频率响应的解析模型，将仿真得到的频变特性下电气参数带入解析模型，通过MATLAB 解析获得频变特性下绕组频率响应。根据基尔霍夫定律建立以电感电流Ii，节点电压Ui为状态变量的绕组状态方程为

其中，

G=2πfCtanδ

式中：M和M1均为由-1，0，-1 组成的系数矩阵，两者互为转置矩阵并乘以-1；I和U分别为包含所有节点的电流、电压列向量；t为时间变量，s；C和L为基于有限元计算所得的电容矩阵和电感矩阵；G为电导矩阵；R为电阻矩阵；tanδ为导体绝缘介质损耗角，（°）。

在绕组模型的外部节点处注入不同频率下的输入电压Ufi，并将其作为已知变量，在另1节点处获得绕组扫频响应，对式（15）变换，得到频变下绕组状态空间方程为

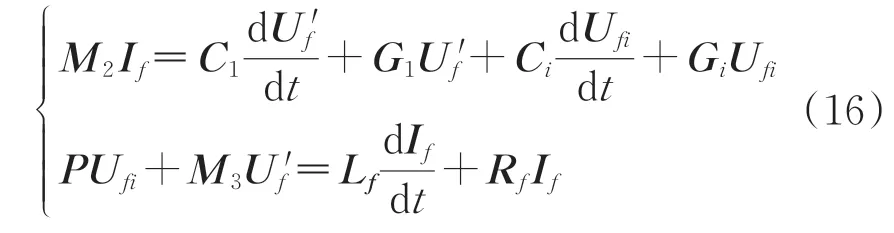
式中：M2为系数矩阵M去掉第i行的系数矩阵；If为不同频率下的电流列向量；f为频率；Uf′为提出Ufi后的电压列向量；Ufi为不同频率下输入节点电压；C1和G1分别为电容矩阵C和电导矩阵G去掉第i行、第i列的参数矩阵；Ci为电容矩阵C去掉第i行之后的第i列向量；Gi为电导矩阵G去掉第i行之后第i列向量；P为系数矩阵M去掉第i行后的第i列向量；M3为M1去掉第i列向量之后的系数矩阵；Lf和Rf为基于有限元计算的不同频率下的电感矩阵和电阻矩阵。

对式（16）化简得到

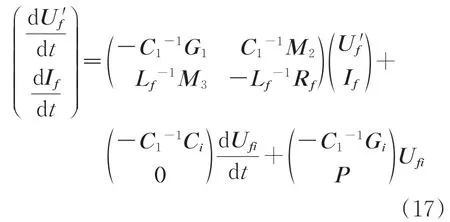
式中：C1-1为C1的逆矩阵；Lf-1为Lf的逆矩阵。

对式（16）进行拉普拉斯变换，得到所有节点相对于输入节点的传递函数矩阵为

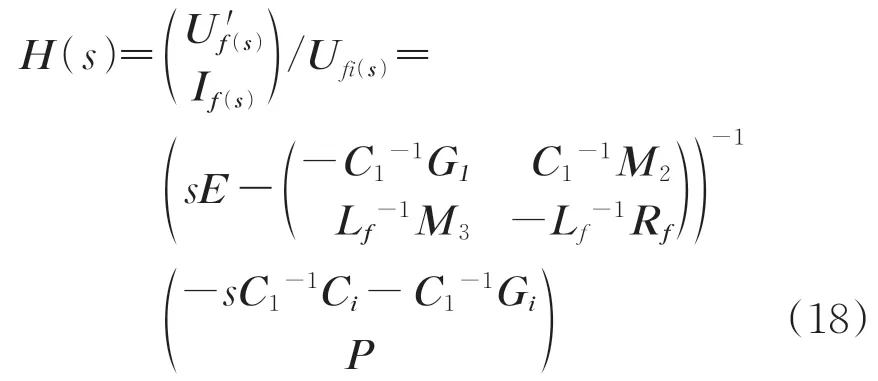
式中：H（s）为绕组传递函数；s为时域函数转换为频域函数时的参数。

为了验证上述建模方法的有效性，针对10 kV/50 kVA 的自耦变压器，在MATLAB 中建立含有144 阶的状态空间方程，将不同频率下的电感矩阵、电阻矩阵带入解析模型，获得频变特性下绕组的频率响应。然后通过实验验证模型的正确性，实验所采用的频率响应测试仪为Megger 公司的FRAX99，频率测量范围为1～1 000 kHz，输出阻抗为50 Ω，测量电压为±10 V。

2.2 频率响应及模型验证

正常情况下变压器绕组的实测与仿真频率响应数据对比如图9所示。由图9可知：考虑频变特性下解析获得频率响应和实测整体趋势一致，其主要谐振点吻合度较高；未考虑频变特性下的频率响应，在低频段（50～100 kHz），谐振点比实测和考虑频变特性下多出2 个谐振点；在中频段（100～600 kHz），未考虑频变特性下频率响应比实测要多出8 个谐振点，其主要特征谐振点1 和2 的频率明显向右偏移，和实测差距较大；在高频段（600～1 000 kHz），谐振点吻合也较低，出现多个误差谐振点，谐振点4明显向右偏移。

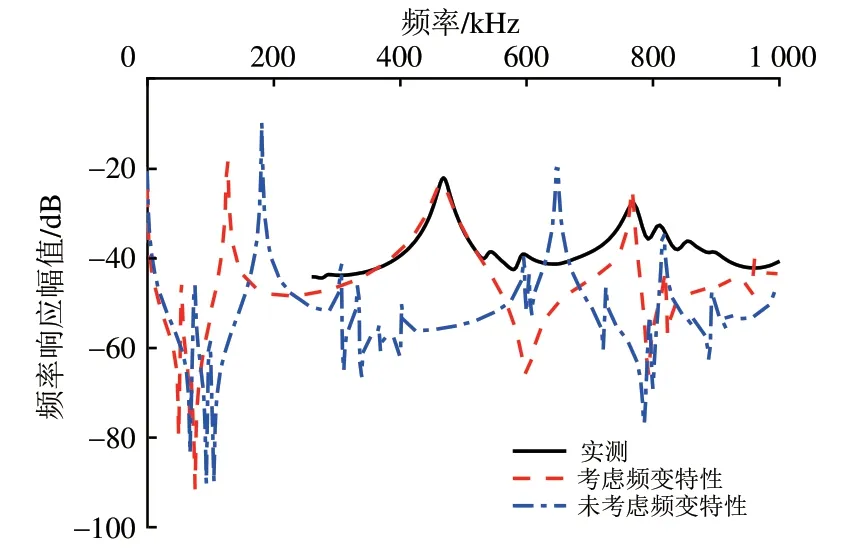
图9 正常情况下实测与解析频率响应对比

正常情况下实测与解析频率响应谐振点频率偏移误差见表2。由表2可知：考虑频变特性实测与解析频率响应谐振频率最大误差约为-3.35%；而未考虑频变特性下选取的5个谐振点频率偏移误差最大为-38.47%，同一谐振点频率偏移误差远大于考虑频变后的误差。造成这种差异主要是由于在频率大于50 kHz时，各绕组的电感均减小约25%，因此在中频段和高频段未考虑频变特性仿真获得的电感和实际值误差较大，导致谐振点偏移误差大以及出现多个误差谐振点。在FRA建模过程中，绕组参数的频变特性对于频率响应的影响不能被忽略。

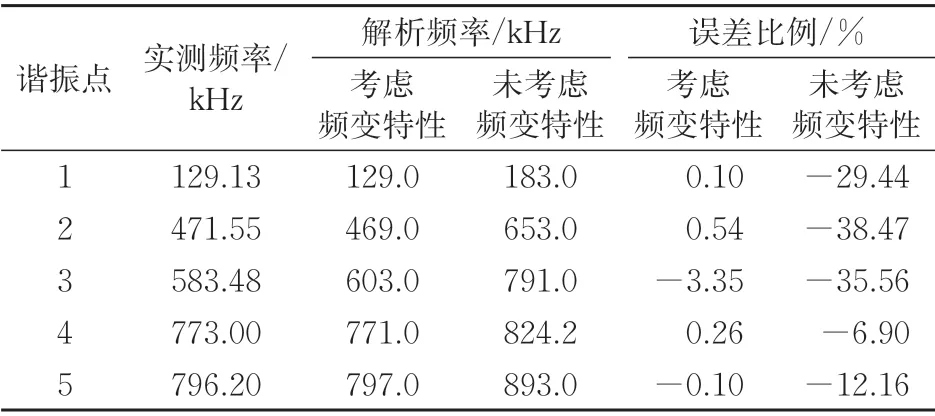
表2 正常情况下实测与解析频率响应谐振点频率偏移误差

轴向移位下实测与仿真频率的响应对比如图10 所示。由图10 可知：轴向移位下解析和实测频率响应变化趋势一致，谐振点吻合较高。计算获得轴向移位下实测与解析频率响应谐振点频率偏移误差，见表3。由表3可知：轴向移位下解析与实测频率响应曲线第2 个谐振点频率偏移量最大仅为5.42%，表明故障下所建立的FRA 模型同样是有效的，可应用于检测绕组故障。

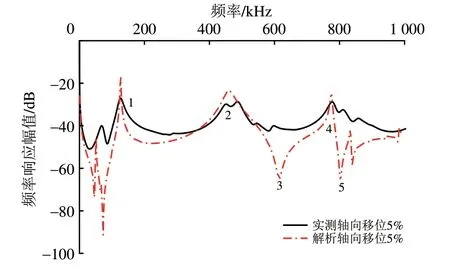
图10 轴向移位下实测与解析频率响应对比

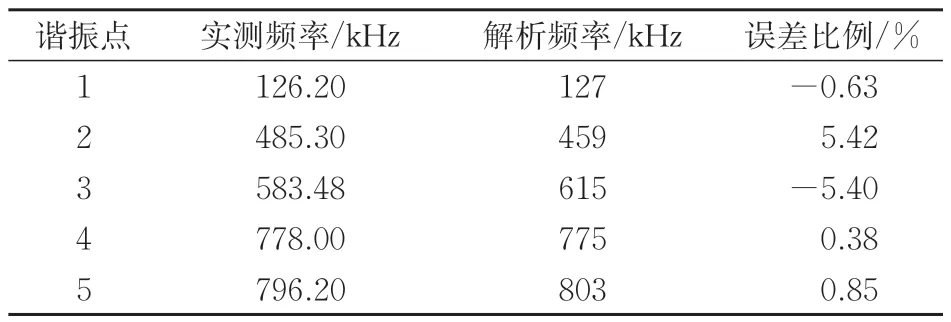
表3 轴向移位下实测与解析频率响应谐振点频率偏移误差

为了分析叠铁心有无梯级对于频率响应模型的影响，分考虑铁心梯级影响和不考虑铁心梯级影响2 种情况，将获得的电感带入频变特性下的解析模型，解析得到变压器叠铁心梯级对频率响应的影响如图11 所示。由图11 可知：未考虑叠铁心梯级影响时，建模获得的频率响应曲线与实测曲线的整体趋势基本一致，但是谐振点偏移误差要比考虑叠铁心梯级影响时的更大。

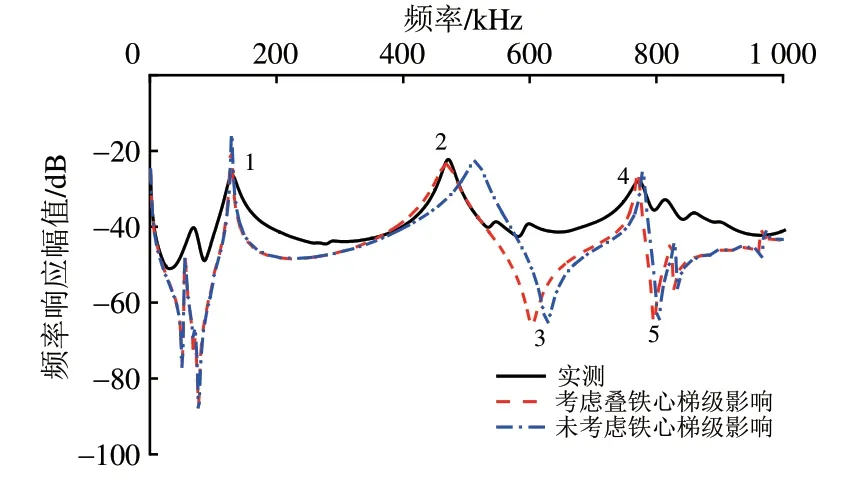
图11 变压器叠铁心梯级对频率响应的影响

频变特性下，考虑叠铁心梯级影响后的谐振点频率偏移误差见表4。由表4可知：未考虑叠铁心梯级影响时，频率响应在中频段第2 谐振点偏移误差最大为-7.9%；考虑叠铁心梯级影响后，频率响应谐振点偏移误差最大仅为-3.35%；考虑变压器叠铁心梯级影响后获得的频率响应准确度更高。

表4 频变特性下考虑叠铁心梯级影响后的谐振点频率偏移误差

3 结 论

（1）变压器叠铁心各向异性相对有效磁导率随着频率的增大逐渐减小，绕组电感也随着频率的增大而减小，而绕组电阻逐渐增大，这是由于高频下受集肤效应和邻近效应的影响。

（2）对于考虑频变特性的绕组模型，仿真获得的频率响应和实测曲线整体趋势基本一致，谐振点频率误差最大值仅为-3.35%，而未考虑频变特性下谐振点频率误差达到-38.47%，实验验证了本文建立模型的正确性，表明该模型能够极大地提高频率响应解析的准确性；解析获得轴向移位5%故障下绕组的频率响应曲线，其主要谐振点与实测的吻合度较高，频率误差最大约为5.42%，表明该建模方法也适用于绕组故障下频率响应建模。

（3）未考虑叠铁心梯级影响时的频率响应曲线整体趋势与实测曲线一致，但是部分谐振点频率偏移量相对较大，最大误差约为-8.48%，而考虑叠铁心梯级影响后频率响应谐振点最大误差仅为-3.35%，因此，考虑叠铁心梯级的影响和频变特性，可提高绕组频率响应的建模精确度。