基于蝙蝠算法的半监督极限学习机在工业检测中的应用*

孙顺远 周 乾

（1.轻工过程先进控制教育部重点实验室 无锡 214122）（2.江南大学物联网工程学院 无锡 214122）

1 引言

在复杂工业中为了获得较好的产品质量，通常需要对关键质量变量进行准确实时的监测，然而这些质量变量大多不易直接测量，如：脱丁烷塔塔底丁烷浓度［1］、青霉素发酵过程产物浓度［2］、水质中微生物浓度［3］等。软测量技术根据易测量到的过程变量信息建立数学模型以实现关键质量变量的实时估计，从而解决上述问题。常用的软测量建模方法有主元回归［4］（Principal Component Regression，PCR）、高斯过程回归［5］（Gaussian Process Regression，GPR）、支持向量机［6］（Support Vector Machine，SVM）、偏最小二乘（Partial Least Squares，PLS［7］）等。

极限学习机（Extreme Learning Machine，ELM）是由Huang［8~9］等提出的一种单隐层前馈神经网络（Single-hidden Layer Feedforward Network，SFLN）训练算法，该算法首先随机赋值给输入权值和偏置，通过激活函数实现非线性转换，再根据最小二乘法求得输出权值矩阵。在极限学习机中，激活函数中的速率参数a和位移参数b以及目标函数中的惩罚系数C对模型精度影响很大。

由于工业过程中确定关键质量变量的值需要花费大量的时间和经济，收集到的大部分数据样本通常只含输入数据、仅有少量数据样本同时包含输入输出数据。一般地，将仅包含输入而缺失输出数据的样本称为未标记样本，将同时包含输入输出数据的样本称为标记样本。若仅采用少量有标记样本对模型进行训练，则软测量模型的预测精度和泛化能力将很难令人满意，并且丢弃大量的未标记样本造成了严重的数据浪费。为此有必要引进半监督学习［10~12］方法，利用大量未标记样本辅以少量标记样本来提高模型的学习性能。常用的半监督学习范式包括分歧式方法、图方法、半监督支持向量机和生成式模型。图方法将数据集之间的联系映射为一个无向图［13~15］，利用流形正则化将未标记数据和目标函数联系起来，是一种广泛采用的半监督学习方法。因此，本文将流形正则化框架引入极限学习机，在充分利用无标记样本信息的同时提高模型的泛化能力。

虽然半监督极限学习机能够在大量无标记样本的情况下有效提升模型精度，但较多的模型参数为优化带来了困难。除传统有监督极限学习机包含a，b，C外，半监督极限学习机又新增了相似度矩阵核宽参数σ和流形正则项的系数λ两个参数。参数对模型精度起关键作用，参数选择不当会造成模型学习性能下降，泛化能力差。为了确定模型参数，可以采用群智能优化算法对模型中的多个参数进行优化。群智能优化算法是一种模拟自然界生态系统机制的优化算法，常见的群智能优化算法有［16~18］蚁群算法、粒子群算法、遗传算法、头脑风暴算法、鱼群算法等。自然界中，蝙蝠生活在黑暗环境中，无法靠视觉识别周围环境，其利用回声定位器发出脉冲，根据反弹回来的回声判断物体的位置、距离、特征。蝙蝠算法［19~20］正是基于此基础上产生的，利用回声定位的原理不断调整脉冲发射度和响度从而寻找到食物，该算法具有结构简单、搜索能力强等特点。

综上所述，本文通过半监督学习方法将少量有标记样本和大量无标记样本结合，并应用于极限学习机模型中；利用蝙蝠算法对模型中的参数(a，b，σ，C，λ)进行全局搜索寻优，得到最优参数的半监督极限学习机软测量模型。此模型不仅解决了极限学习机收敛性差的问题，同时也克服了随机选取参数导致精度不稳定的问题，提高了模型的预测精度。最后，将本文方法应用于污水处理中生物需氧量含量和脱丁烷塔塔底丁烷浓度的仿真实验研究，与不同的建模方法比较后，验证了该方法的有效性和适用性。

2 半监督极限学习机

2.1 极限学习机原理

极限学习机是由Huang 提出的一种单隐层前馈神经网络（Single-hidden Layer Feedforward Networks，SLFNs）学习算法，该算法首先确定隐含层神经元节点个数，再随机赋值给输入层的输入权值和偏置，通过最小二乘方法求解得隐含层和输出层之间的输出权值。该算法不仅克服了传统梯度算法的复杂迭代问题，而且其训练速度快、泛化能力强。极限学习机用于回归问题时，训练的步骤分为随机学习和计算输出权值。

极限学习机的训练目标为最小化预测误差，其目标函数为

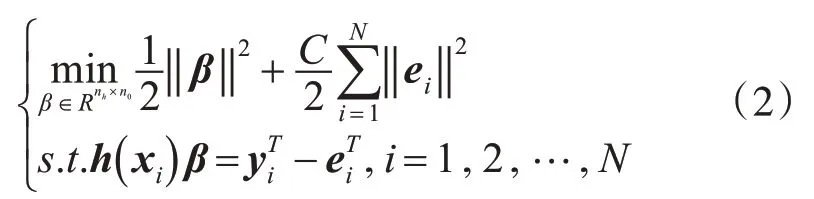
其中ei∈Rm为第i个输出样本的训练误差，C为惩罚系数。

将约束条件带入目标函数后，可转换为无约束优化问题：

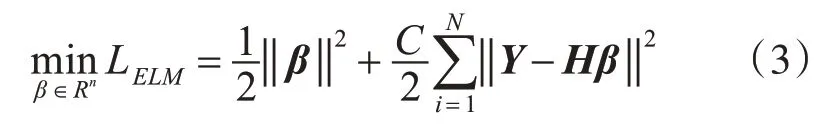
上述函数可认为是岭回归的问题，将LELM相对于β的梯度设为0，得到：

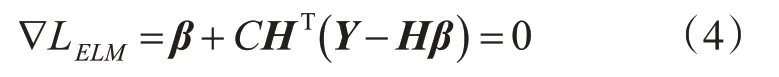
于是可将输出权值β表为

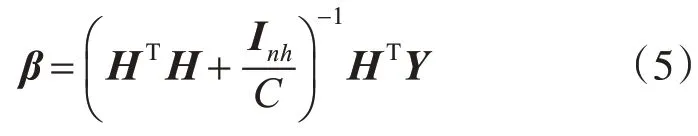
2.2 流形正则化框架

流形正则化的本质是将原特征空间的数据映射到新的空间［21~22］，并保留原特征空间中数据的局部几何关系，旨在充分挖掘数据的非线性几何特性。需最小化的目标函数如下：

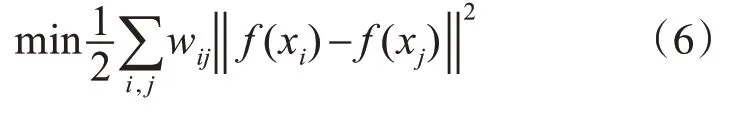
其中f(xi)和f(xj)分别是输入样本xi和xj的模型预测输出，wij是xi和xj间的相似度。采用高斯函数计算相似度，可得相似度矩阵W：

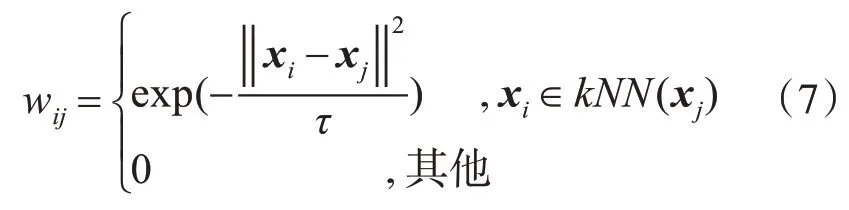
其中kNN(xj)表示样本xj的近邻。

通过数学计算将目标函数展开：

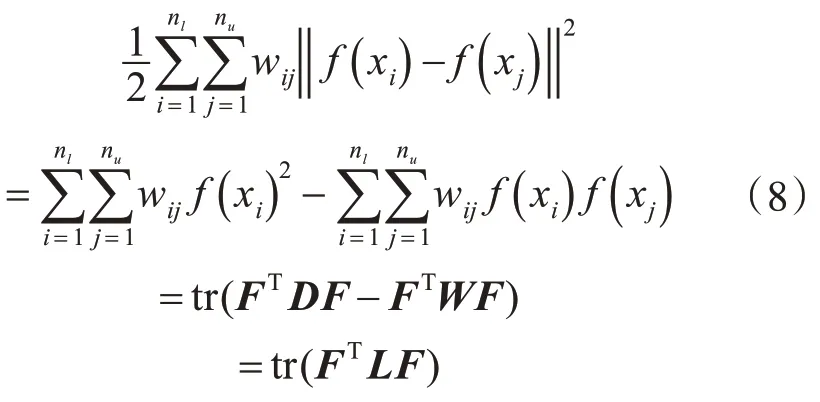
其中，tr(·) 表示矩阵的迹，nl为标记样本个数，nu为未标记样本个数，为 模 型 预 测输出，矩阵L=D-W是拉普拉斯矩阵。

2.3 流形正则化框架与半监督极限学习机结合

半监督极限学习机采用流形学习，通过样本间的几何关系让未标记样本辅以标记样本学习。利用流形正则化将几何关系与预测误差联系起来，提升模型的预测精度。

在半监督极限学习机训练过程中，不同类的数据对训练效果的影响不同。模型倾向于训练所含样本个数较多的类，为了提高模型的预测精度，在预测误差前各加不同的惩罚系数因子，以此平衡各个类中数据对模型的影响程度。假设训练样本中xi属于类ti，类ti中含Nti个训练样本，对每个样本的预测误差乘以一个惩罚参数Ci：

其中C为惩罚系数。由此将半监督极限学习机约束问题转换为无约束问题：

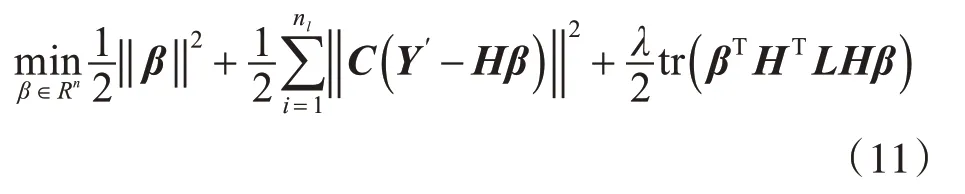
其中，Y′为根据实际输出样本扩展得到的，前s 行为标记的输出样本，其余行均为0 ；C=diag(C1，…，Cnl)为惩罚系数组成对角矩阵。通对式（12）求β的梯度，可得

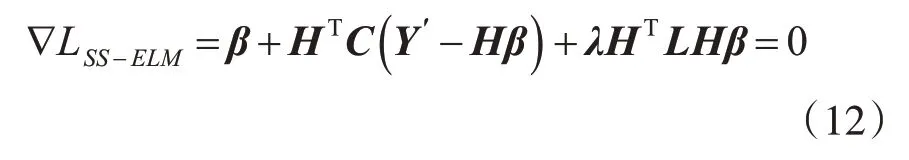
求解可得：

3 蝙蝠算法

蝙蝠对自身发出超声波及接收到回声的时差建立周围环境的映像，利用回声定位原理感知食物的距离、大小及运动方向。蝙蝠算法是模仿蝙蝠搜寻食物的过程而演化出的一种优化算法，首先初始化每只蝙蝠的位置和速度，把蝙蝠的位置看成待寻优问题的解，在每次迭代后对每只蝙蝠相对应的适应度函数值进行排序，找出位置最佳的蝙蝠xb。每次迭代中，利用回声定位原理进行位置和速度的更新，其中频率决定了蝙蝠搜索的范围，如下：

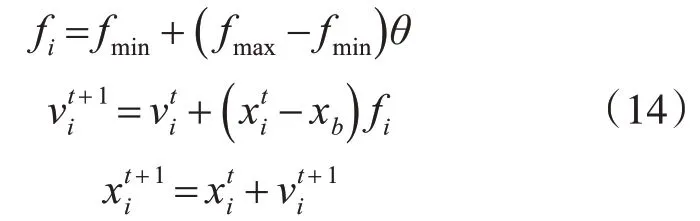
其中，θ均匀分布在[0 ，1] 中，fi表示第i只蝙蝠的当前频率值，fmax和fmin分别代表蝙蝠搜索频率的最大值和最小值表示第i只蝙蝠在t 时刻时的速度，表示第i只蝙蝠在t时刻时的位置。

在迭代时，对当次迭代的最优位置进行局部寻优，探索最优解的附近区域。在最优位置附近随机生成一个新的解：

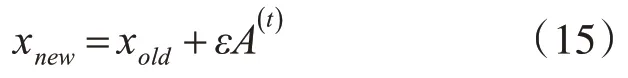
其中，ε是[- 1，1] 中的随机数，A(t)为t 时刻所有蝙蝠的平均响度，xold为当前最优位置。

在蝙蝠靠近食物时，会加快脉冲发射速率并减小响度，直至吃到食物。在蝙蝠算法的寻优过程中，没找到一个最优位置时，频度r和响度A均会进行相应的更新：

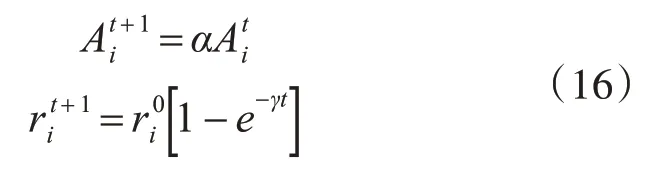
其中α∈( 0，1) ，γ＞0，通常取：α=0.9，γ=0.9。脉冲频度和响度的变化一定程度上反映着距离目标的远近程度。

综上所述以上分析，蝙蝠算法步骤为

1）初始化蝙蝠个数n1、迭代次数N1、维数d、位置xi、速度vi、频率范围[fmin，fmax] 、频率fi、初始脉冲频度Ai和响度ri；

2）定义适应度函数q(x)；

3）根据频率fi对每只蝙蝠的位置和速度进行更新；

4）若满足(rand＞ri)，在最佳位置处随机产生一个新的位置x′；

5）根据新的位置求出qnew，若满足(rand＞Aiq(x′)＜q(xb))，接收新值并对频度和响度进行更新；

6）根据各只蝙蝠的适应度函数值重新排列选出当前时刻的最佳位置；

7）迭代次数未达到设定次数，返回至3）；

8）输出迭代N1次后的最佳位置xb。

蝙蝠算法中的位置和速度更新方式类似于标准粒子群算法中的更新方式。不过，在蝙蝠算法中，通过调节频率fi大小进而控制每只蝙蝠的搜索范围。所以，蝙蝠算法的突出特点是使用频率和参数调整进行全局寻优。

4 基于蝙蝠算法的流形正则化半监督极限学习机

基于流形正则化的半监督极限学习机的性能受多个参数影响：激活函数中的速率参数a与位移参数b、核宽σ、惩罚系数C和权重λ。参数选择不当时，会大大影响模型的预测输出。为提高模型的预测精度，利用蝙蝠算法对基于流形正则化的半监督极限学习机进行参数寻优，每只蝙蝠的位置相当于待寻优的最优解组合(a，b，σ，C0，λ)。

图1 为蝙蝠算法优化半监督极限学习机的流程。

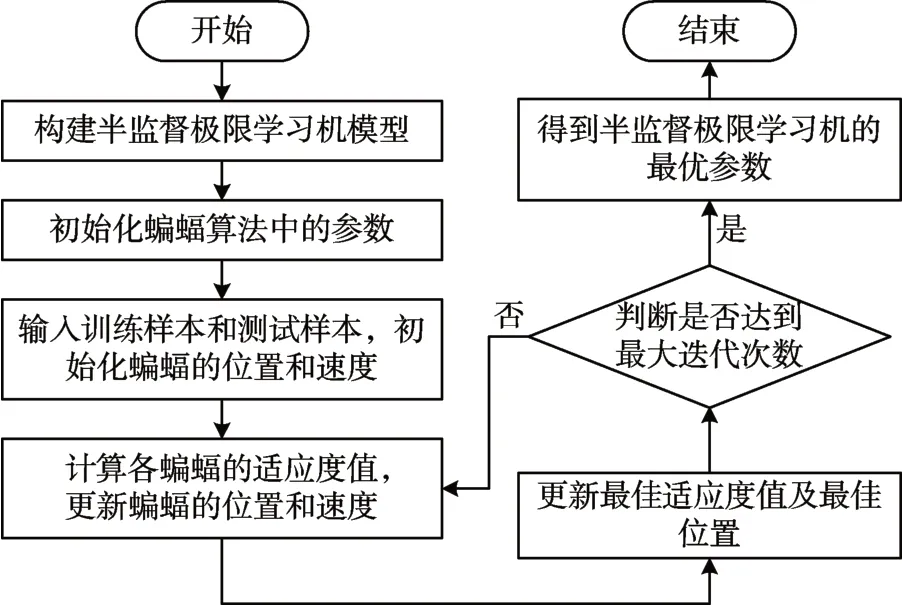
图1 BA优化SS-ELM参数的流程图

基于蝙蝠算法的半监督极限学习机的训练步骤为

Step1：根据收集到的训练样本，构建半监督极限学习机网络结构；

Step2：初始化蝙蝠算法相关参数：蝙蝠个数n1、迭代次数N1、维数d、速度vi、频率范围[fmin，fmax] 、频率fi、初始脉冲频度Ai和响度ri；

Step3：随机产生一组数据(a，b，σ，C0，λ)作为蝙蝠的初始位置xi；通过比较每只蝙蝠对应的适应度值更新各自的速度和位置；

Step4：判断迭代次数是否达到设定次数，若达到，得到蝙蝠的最佳位置xb，即模型的最优参数；否则继续对模型参数进行迭代寻优；

5 仿真研究

脱丁烷塔过程是工业石油炼制中脱硫和石油脑分离的组成部分［23］，塔底丁烷浓度对炼制出的石油品质影响很大且不易通过在线仪器直接测量。在工业生产中需要对其严格监测和控制，为此采用软测量技术对丁烷浓度进行预测。图2 为脱丁烷塔过程示意图。

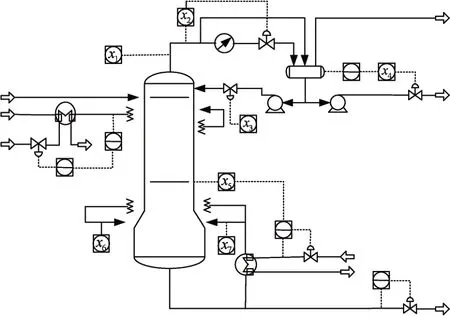
图2 脱丁烷塔过程示意图

选取脱丁烷塔过程中易测得的7 个变量为辅导变量，作为软测量模型的输入，各辅助变量的说明如表1 所示，相应的辅助变量测试仪器安装位置标注在图2 圈出部分；主导变量为脱丁烷塔塔底丁烷浓度。

表1 脱丁烷塔的输入变量及其描述

共收集到2000 组过程数据，其中1000 组作为训练样本，剩下1000 组作为测试样本，接着对训练样本作归一化处理。基于以上数据集分别建立三种软测量模型：有监督ELM 模型、半监督ELM 模型和蝙蝠算法优化的半监督ELM 模型，进行实验仿真并比较各模型效果。采用均方根误差RMSE和相关系数COR作为模型的性能指标：

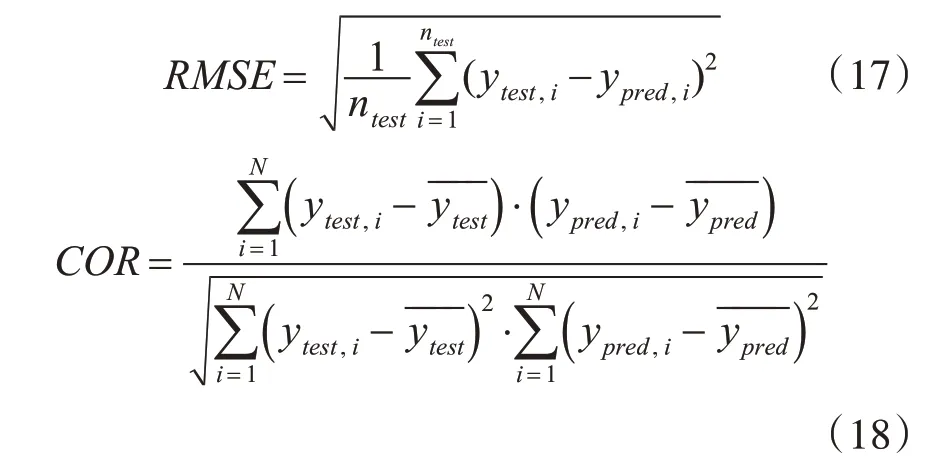
其中ntest是样本个数，ytest，i和ypred，i分别表示第i个测试样本的真实值和预测值，而- ---ytest和- -----ypred分别为测试样本真实值和预测值的平均值。

表2 所示为三种软测量模型的预测结果，分析可得：在有标记样本数量较少时，有监督的ELM 并不能较好地预测丁烷浓度；为利用大量无标记样本，引入半监督学习后一定程度上能够提高模型的预测精度；由于半监督ELM 模型中含5 个参数：a，b，σ，C0，λ，这些参数选择的不同，会造成模型的预测精度不稳定，故利用优化算法找到模型的最优参数。在半监督ELM 中引入蝙蝠算法，利用其回声定位原理快速找到模型的最优参数，能够提高模型的预测精度。由此可见，本文方法能够有效预测脱丁烷塔塔底丁烷的浓度。

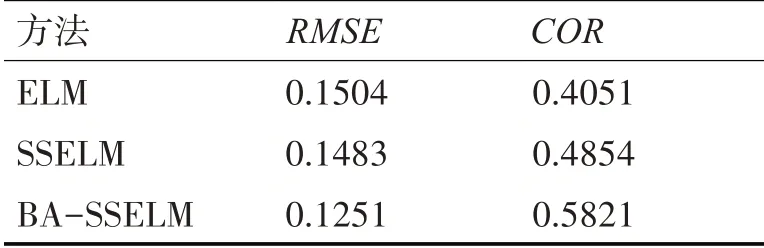
表2 三种建模方法的预测结果比较

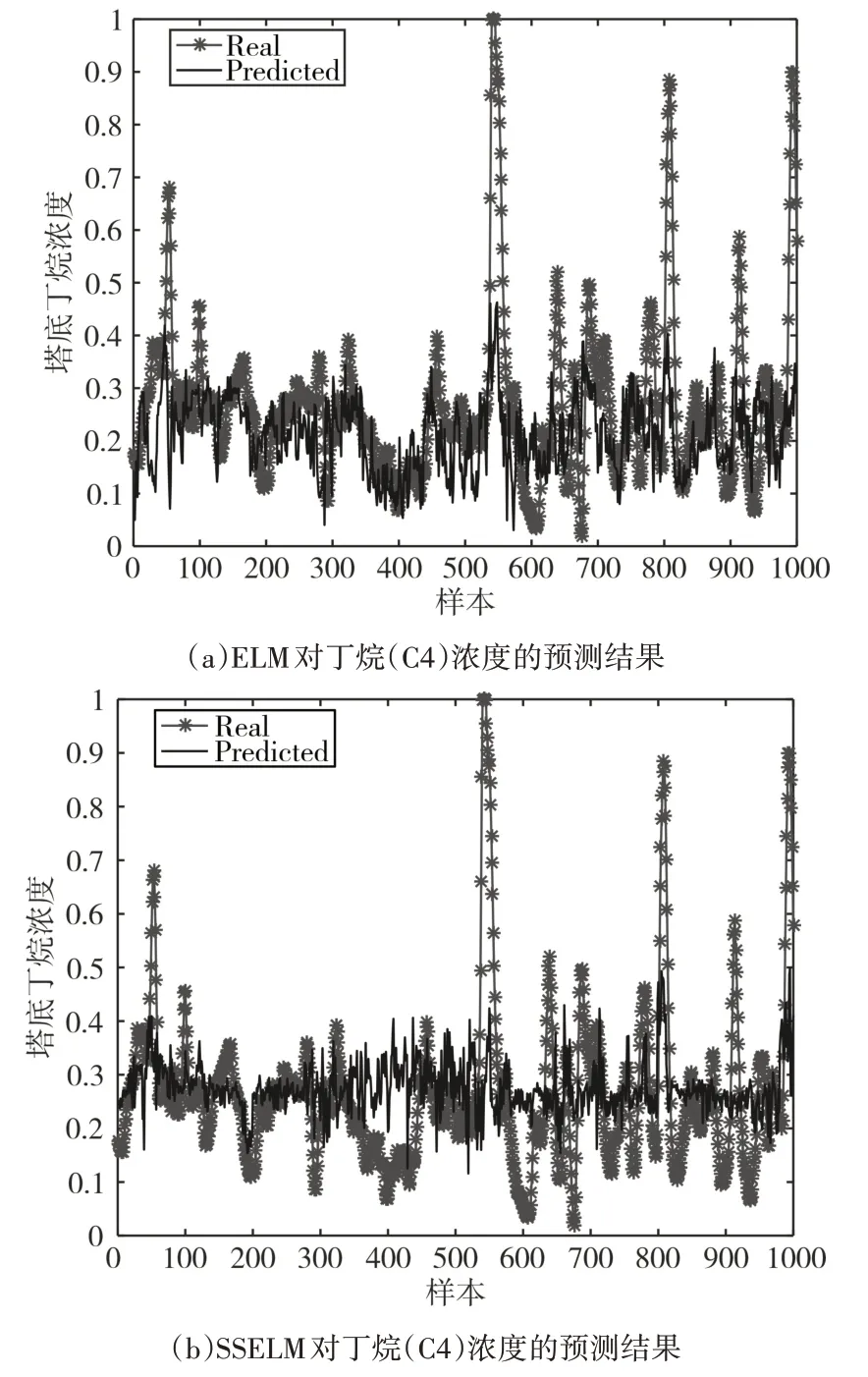
图3 所示为三种模型的仿真结果，由图比较分析可得：BA-SSELM 模型对脱丁烷塔塔底丁烷浓度的预测值与真实值较为接近，利用蝙蝠算法较好的全局寻优性能，能够快速找到适合模型的全局最优参数，使得模型的输出紧凑地跟随实际值的变化，说明BA-SSELM模型的预测结果较准确，对丁烷浓度的预测效果更佳。相比于有监督极限学习机，本文所提方法对丁烷浓度的拟合效果更好，预测精度也更高。

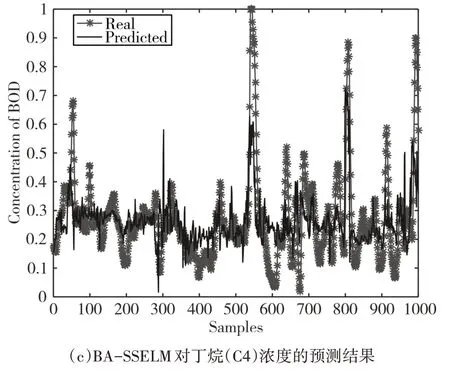
图3 ELM、SSELM、BA-SSELM的仿真结果

6 结语

为充分利用训练样本集中的无标记数据，通过流形正则化框架，在极限学习机中采用半监督学习方法。并利用蝙蝠算法对半监督极限学习机模型中的a，b，σ，C0，λ这五个参数优化以获得模型的最优参数，从而提高模型的泛化能力。通过污水处理中BOD 含量和脱丁烷塔塔底丁烷（C4）浓度的仿真实验，验证了本文方法能够提高对工业过程中关键质量变量的预测精度并具有较好的泛化性能。