基于灰色关联分析和模糊综合评价算法的城市发展程度研究*

桂永杰 吴世宝 马瀚龙 马 佳

（1.沈阳航空航天大学计算机学院 沈阳 110136）（2.沈阳航空航天大学航空宇航学院 沈阳 110136）（3.沈阳航空航天大学创新创业学院 沈阳 110136）（4.沈阳航空航天大学理学院 沈阳 110136）

1 引言

随着近几年国家经济实力的不断增长，国内主要城市的经济实力与发展前景也出现了此消彼长的变化。例如随着改革开放的不断深入，东南地区的经济实力不断增长，而东北地区却陷入了人口增长停滞以及经济衰退的现象。一个区域的城市发展程度影响了国家对该地区相应的政策制定以及扶持资金的发放。于是对于不同地区城市发展程度的评级和排名就显得尤为重要。

城市发展程度以及经济实力相关的评价和排名的研究较为广泛。许多学者以不同的方式对城市发展程度进行了研究。王泽宇等［1］以综合赋权为基础的模糊物元模型和核密度估计模型等评价方法，对2000~2012 年中国城市经济转型成效的时空格局演变进行分析。刘艳芳［2］采用主成分分析法构建综合评价模型并根据评价得出国内30 个主要城市经济发展质量的差异。刘振锋等［3］选取2003、2008、2012 年三个时间断面的数据对全国283 个地级及其以上城市经济实力进行了评价分析。张赛飞［4］利用主成分分析法对珠江三角洲、长江三角洲24城市的经济实力进行了相关的分析和研究。

但以上的研究也有一定的缺点，例如所取数据较为古老，对于如今城市发展程度的研究已经不太适用。同时有较为多的研究使用主成分分析法进行相应的分析，但主成分的解释其含义一般多少带有模糊性，不像原始变量的含义那么清楚、确切。本文在以上的研究基础上，对如上缺点进行改进，并对国内19 个城市进行了评价模型的构建以及发展程度的分析。

城市经济活力，是指城市经济发展过程中的能力和潜力［5］。本文以城市经济活力作为指标，以北京为例，利用灰色关联分析分析出不同因素对经济活力的关联度［6-8］，之后利用模糊综合评价［9］对不同城市的经济活力进行评价分级，最后得出了国内不同城市经济活力的排名与分级。该项研究对于指导国家相关政策的实施，以及明确城市定位，以及作为城市规划参考具有重要的意义。

2 经济因素与经济活力的关系模型

公司数目对区域经济活力产生积极影响［10］，只要找到其与某些指标之间的关系，例如永久居民的人口或GDP，以及一个地区内公司的数量，就可以代指这些经济因素与经济活力之间的关系。灰色关联分析（GRA）是一种多元统计分析方法，假设一个因素和许多其他因素之间具有关系，找到哪个因素与该指数关系更紧密，哪个因素与该指数关系更弱就显得非常有必要。在此分析的基础上，采用灰色关联分析模型，以北京为例来解说明问题。

2.1 数据来源

为了获取可用于分析的数据，本文从《中国统计年鉴》和《北京市2012 年国民经济和社会发展统计公报》中收集了一些官方数据［11~16］，用作灰色关联分析模型的数据源。表1和表2列出了本文收集的数据。

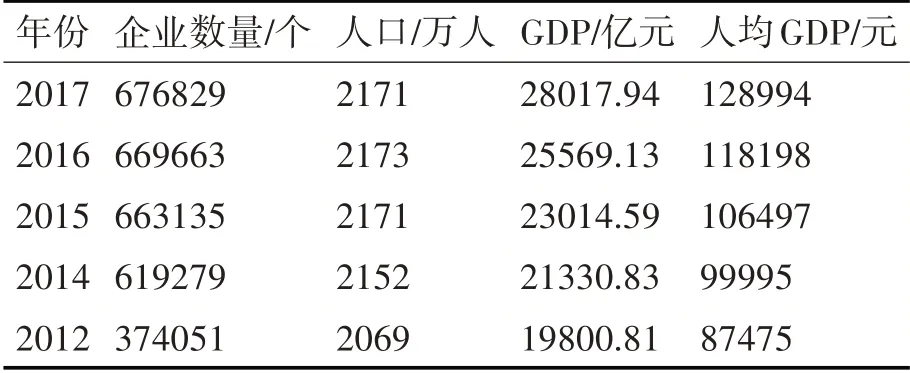
表1 北京的几个经济因素（a）

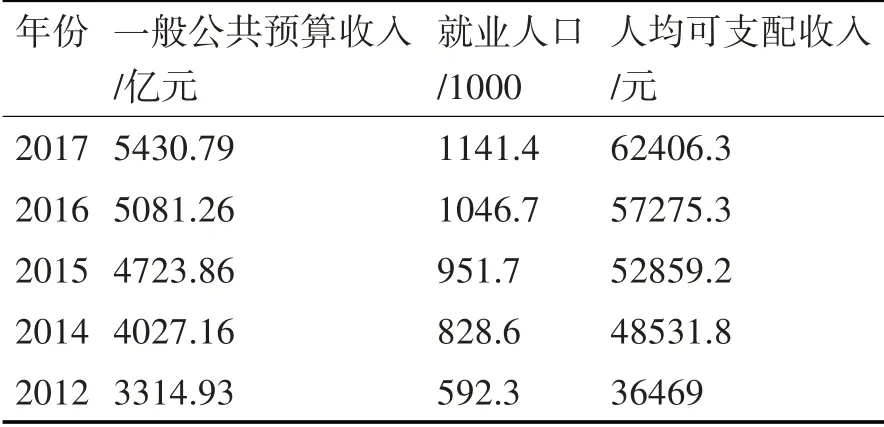
表2 北京的几个经济因素（b）

2.2 模型建立

本文使用表1和表2中的数据来建立数据序列矩阵。如式（1），m 是评估指标的数量，n 是因素的数量。在此模型中，m等于5，n等于6。

参考数据列应是理想的比较标准，选用公司数量作为参考数据列，如式（2）所示。

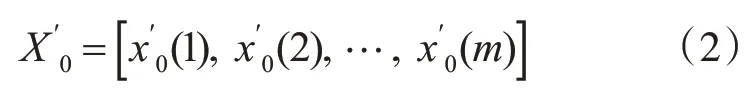
鉴于各个因素的实际含义不同，数据的无量纲是灰色关联分析中的必要过程。选用平均值作为无量纲方法，如式（3）所示。

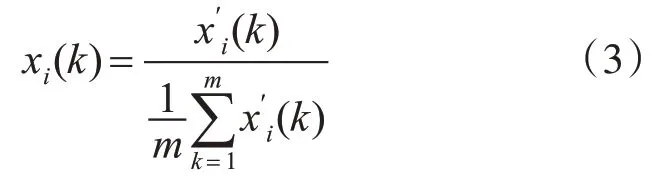
计算被评估对象的索引数据列（比较数据列）与参考数据列之间对应元素的绝对差，得到ξi(k)。

相关系数是比较序列与参考列之间始终的相关度值。相关性的计算公式如式（4）所示。

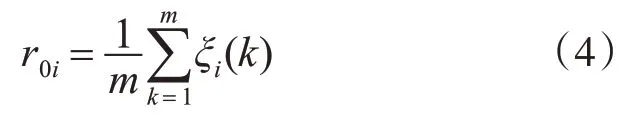
2.3 模型求解

求解该模型，本文获得了经济因素与公司数量之间的相关性，如表3和表4所示。

如表3 和表4 所示，工作数量和人均可支配收入与公司数量之间的关系更为密切，这表明工作数量和人均可支配收入将对公司数量产生积极影响。GDP，人均GDP，就业人数和地区人均可支配收入这四种因素得到提高，区域经济活力就会得到改善。

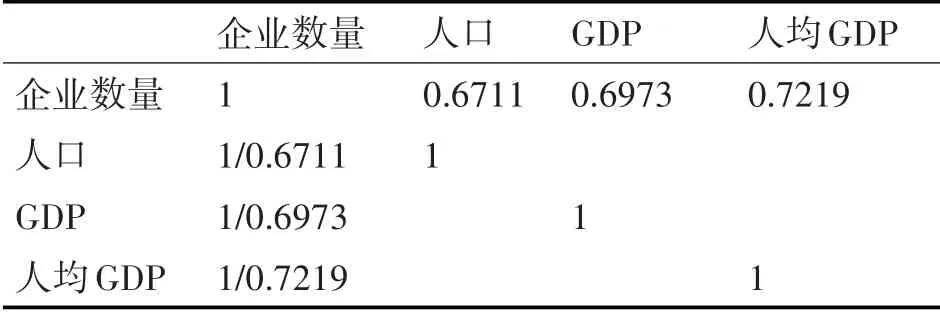
表3 经济因素与公司数量的相关性（a）

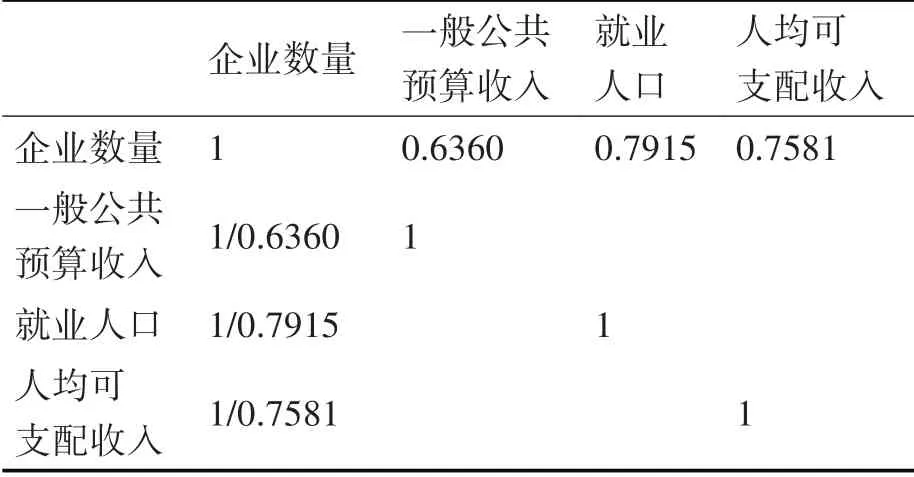
表4 经济因素与公司数量的相关性（b）

3 区域经济活力的衡量

根据2.3 小节部分模型求解出的相关性，选择4 个更接近经济活力的变量，包括GDP，人均GDP，就业人数和地区人均可支配收入。将这些因素作为评估附录中城市经济活力的标准。然后，归一化上述四个因素与公司数量之间的相关性，以此作为权重。之后结合收集到的实际数据，确定4 个评价等级，建立隶属度函数，得到得分矩阵。基于城市等级，本文将不同城市分为四个等级，用于对城市的经济活力进行排名。

3.1 模型建立

将4 个变量的数据分为4 个部分，步长为d。同时，确定19 个城市的相关数据的最大值为max，最小值为min，如表5和表6所示。

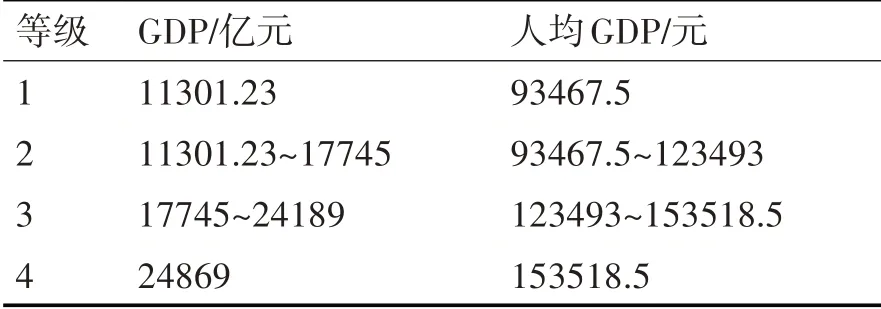
表5 四个因素的四个层次（a）

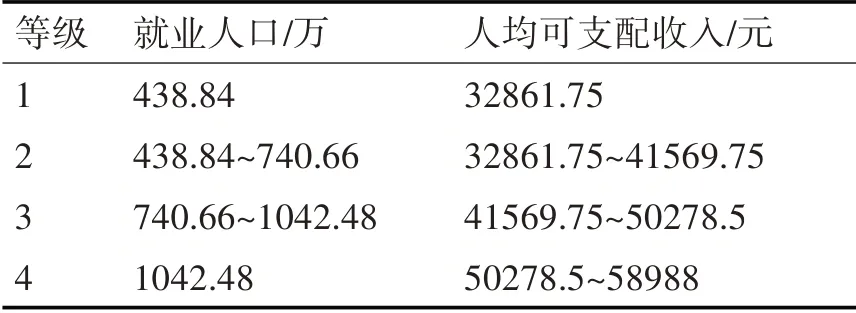
表6 四个因素的四个层次（b）

定义了一个因子集U，如式（5）所示。

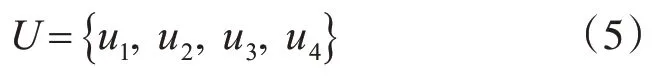
对在2.3小节部分中计算出的相关性进行归一化。然后，将权重向量A确定为式（6）。

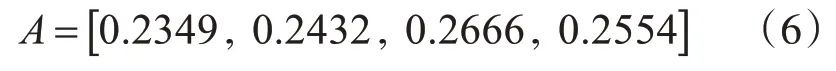
定义了注释集V，级别越高，经济活力越好。

在4 个因素和评论级别之间建立梯形隶属函数C1（u1）、C2（u2）、C3（u3）和C4（u4）。

图1，2，3，4 展示了不同隶属度函数的图像。基于模糊评估矩阵，定义了一个综合评估矩阵B，如式（8）所示。

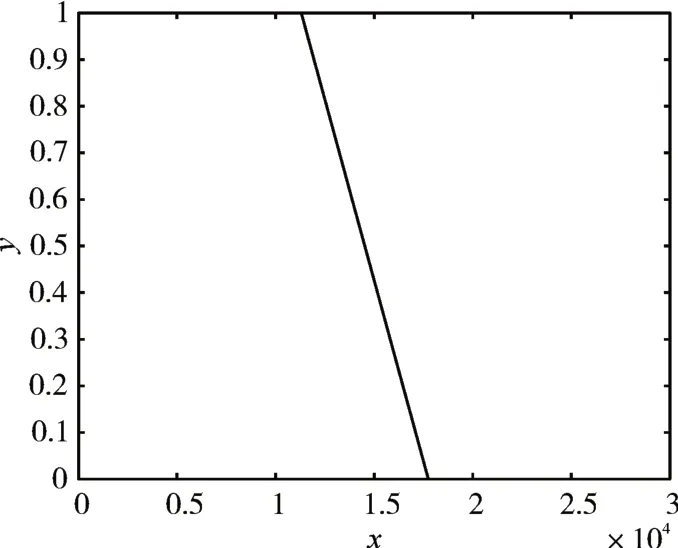
图1 隶属度函数C1（u1）

将矩阵B 归一化，在公共集合中选择与矩阵B中最大元素的索引相对应的评估级别。假设城市与该级别之间的成员资格为最高成员资格，该城市被分类为该等级。

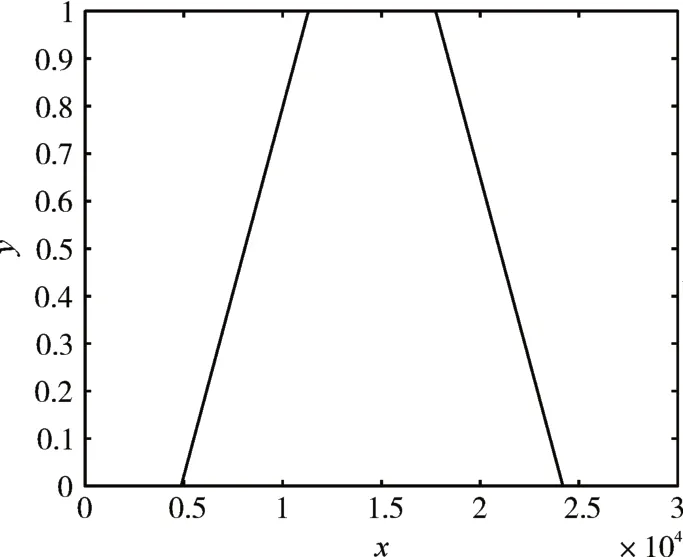
图2 隶属度函数C3（u3）

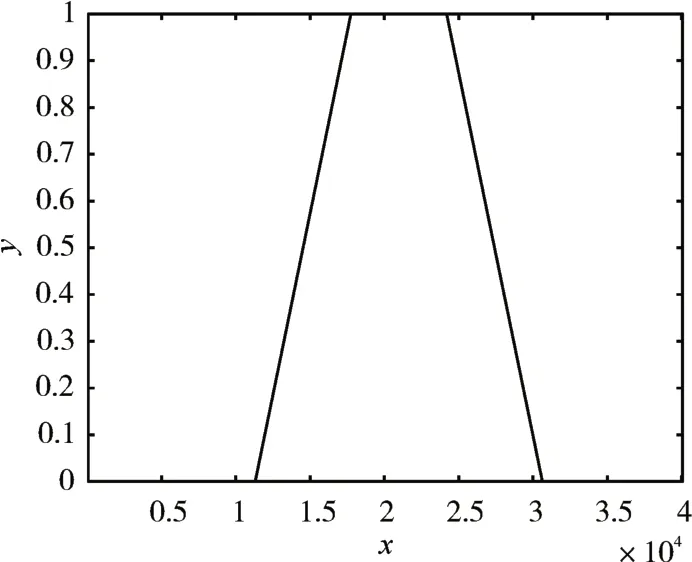
图3 隶属度函数C3（u3）

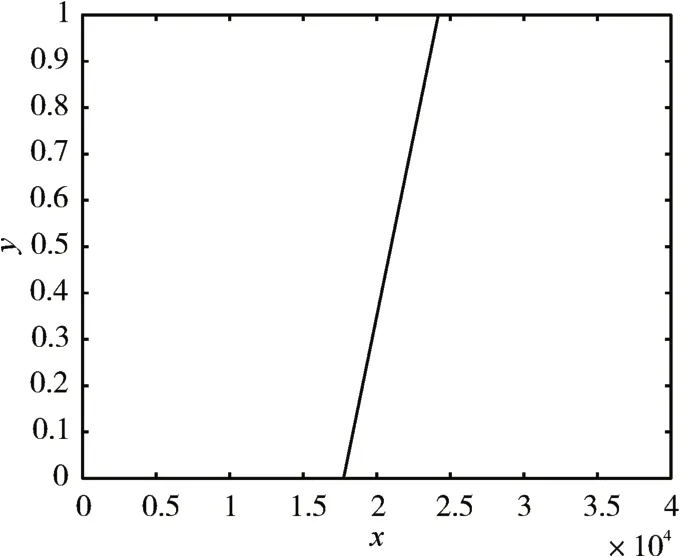
图4 隶属度函数C4（u4）

3.2 模型求解

如表7 所示，4 级城市有3 个，分别是深圳、北京和上海；有2 个城市的等级为3，即广州和杭州；有10 个城市的等级为2；其他城市的等级为1。正如本节序言当中对级别的定义，级别越高，经济活力越好。如表7所示，该模型计算的结果与实际的城市经济水平与发展程度较为吻合，具有较高的可靠性。

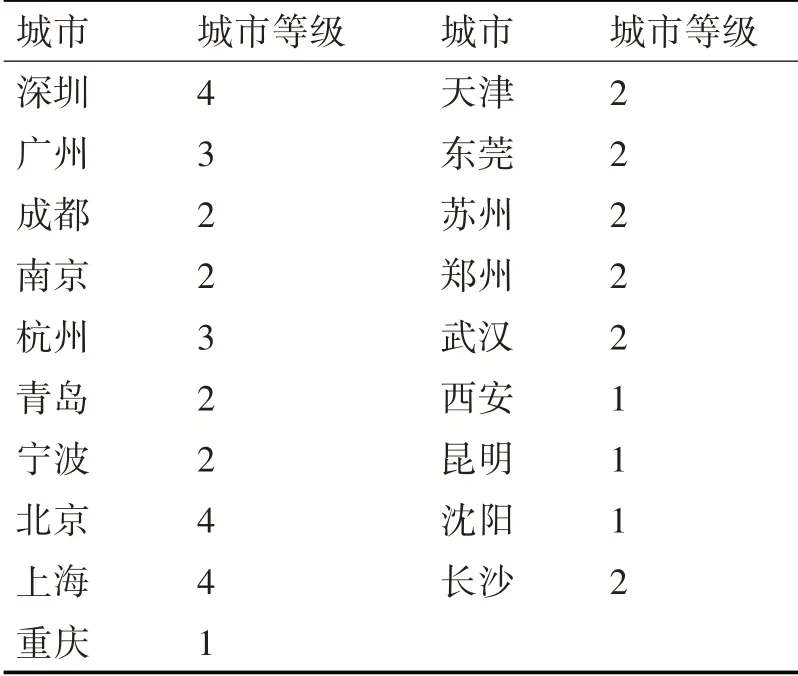
表7 不同城市的等级

4 结语

本文首先建立一个可以分析不同经济因素对公司数量影响的模型。以北京为例，本文收集了近5 年的7 种数据，然后用灰色关联分析法计算了其他6个因素与公司数量的相关性。定义了4个评估级别，利用模糊综合评价法，将一些城市分为4 个等级，对城市的发展程度进行了排名。利用相关的数据进行分析和排名，对于经济活力相关因素的分析和城市发展程度的排名较为客观，可为政府的政策制定和相关投资人员的投资分析提供了于可靠的依据。同时本模型还可用于对城市其他指标进行类似的分析与研究，如对医疗系统，教育水平等因素的评价，具有较为广泛的应用价值。