基于优化无迹卡尔曼滤波的注入信号检测*

经鹏宇 庞科旺 吴 拓

（江苏科技大学电子信息学院 镇江 212000）

1 引言

在船舶电力系统中，电缆是舰船不可缺少的电气设备。电缆绝缘的优劣，直接影响舰船供电的安全性和可靠性，所以准确地对舰船电缆绝缘状态进行监测，具有重要的应用价值。根据相关规定，船上的电力电缆需要定期进行维护和检查与维修［1］。但是由于船舶的特殊性，电缆的安装密度相当大，安装位置分散，所以电缆故障检测过程复杂［2］。传统的检测方法多是在断电的情况下进行检测，检测周期长。随后直流叠加法、介质损耗因数法、接地电流法等方法被用来进行电缆绝缘状态的在线监测［3~5］。近年来，有通过低频注入法进行绝缘监测［6~8］，但低频情况下，电缆对地的分布电容会呈现低阻状态，不但绝缘电阻监测的精度会受到很大的影响，而且低频电源变压器的制作也非常不便。

近年来，针对低频注入法的不足，有采用混频注入的方法，通过注入两个相乘的接近于工频的正弦交流信号，可分别得到一个二倍工频和一个低频正弦交流信号，对注入的电流的幅值进行检测，从而计算出电缆的接地电阻和电容。船舶电网中噪声复杂，干扰较大，能否对注入电流进行精确检测直接有影响着电缆绝缘状态监测的精度。

无迹卡尔曼滤波是一种基于无迹变换的非线性卡尔曼滤波器［9］，拥有计算量小、跟踪能力强等特点，广泛运用于电力系统的稳态和暂态分析中，常规无迹卡尔曼状态噪声协方差和观测噪声协方差一般取常量，误差较大。为提高测量精度，本文利用粒子群优化算法对无迹卡尔曼滤波算法的状态噪声协方差和观测噪声协方差进行优化，能够有效地提高电流的检测精度。

2 注入信号模型

混频注入法通过向乘法器注入两个相乘的接近于工频的正弦交流信号，由三角变换公式可得相当于注入两个频率分别为ω1+ω2和ω1-ω2的信号，令ω1、ω2之和为100Hz 则分别得到一个二倍工频和一个低频正弦交流信号，这样可以提高舰船电缆对地电阻和对地分布电容的监测精度。注入信号经离散化可表示为

其中ωL=ω1-ω2，ωH=ω1+ω2。

则含注入信号和n 次离散化谐波信号可表示为

3 粒子群优化UFK算法的基本理论

3.1 UFK算法的基本理论

UFK 是一种以无迹变换为基础的非线性卡尔曼滤波器，该方法通过找到一组sigma点，经非线性函数变化，得到均值和协方差并以此来估计非线性函数真实的均值与协方差。UFK的具体流程如下。

1）建立模型

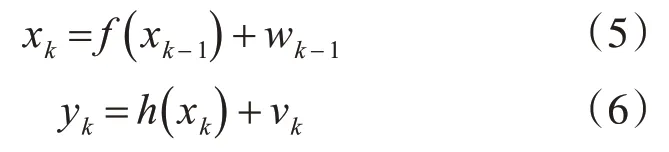
式中xk和yk是k 时刻的n 维状态变量的m 维观测值；wk-1~N（0，Qk-1) 是k-1 时刻的过程噪声；vk~N（0，Rk)是k时刻的测量噪声。

2）状态向前一步预测

假设k-1 时刻的状态分量xk-1~N（x̂k-1，pk-1)，则可产生一系列sigma点，sigma点的产生方法可以采用简单无迹变换，也可以采用一般型无迹变换或者球形无迹变换，这里采用简单无迹变换产生sigma点：

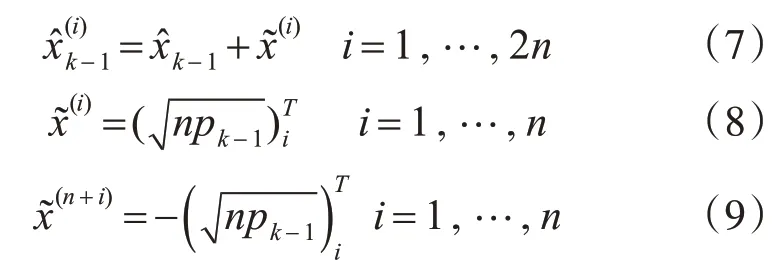
通过系统方程将sigma点转换为x̂(i)k：

合并向量得到k时刻的均值和协方差：

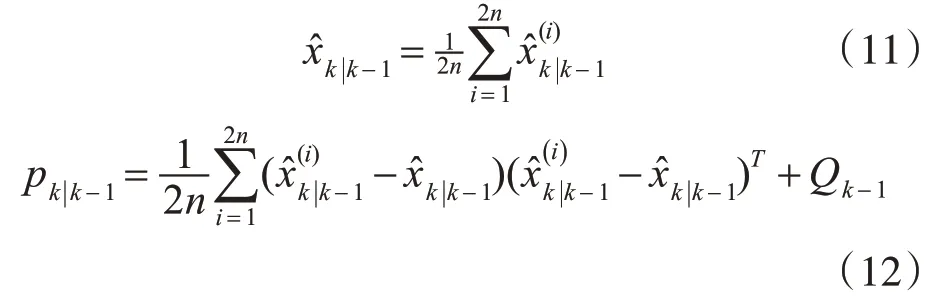
3）测量更新

根据当前xk的均值和协方差的最好估计，生成新的sigma点：

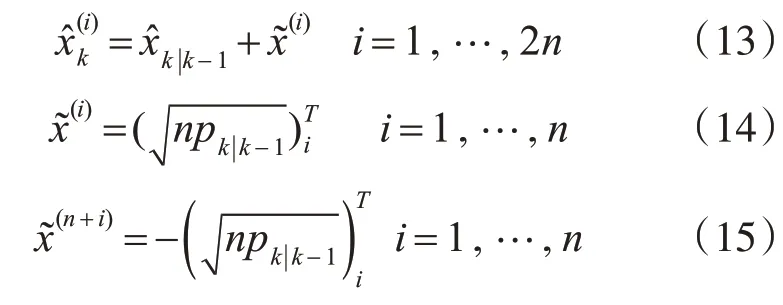
通过测量方程将sigma点转换为

合并向量得到经过测量方程传递的均值、协方差和互协方差：

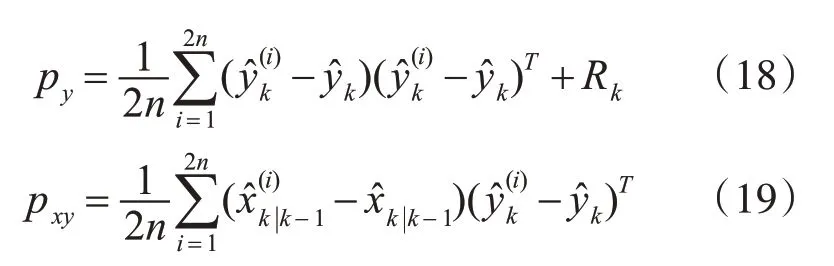
最后进行状态的测量更新：

3.2 粒子群优化协方差

粒子群优化算法于1995 年由Eberhart 和Kennedy提出［10］。它是从随机解开始，然后通过每次迭代的过程中在解空间中寻找全局最优解一种进化算法［11］，其中最优解通过适应度这个值来评价。因为没有交叉和变异，所以规则相对简单，容易使用，收敛快，因此被广泛使用。

粒子群经过初始化后，然后得到了一群随机解。根据以下两个公式不断地迭代更新粒子的速度和位置，从而可以找出问题的最佳解［12~14］。

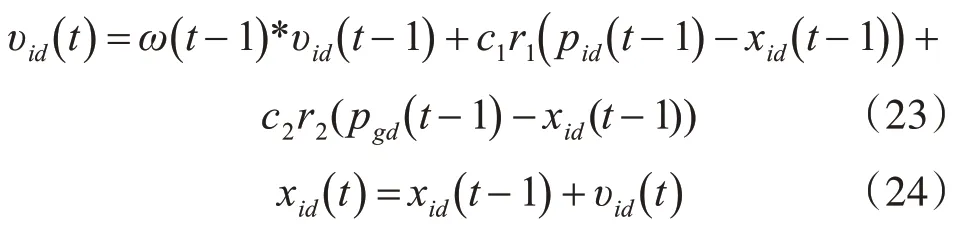
式中，r1，r2是介于（0，1）之间的随机数；ω(t-1) =(ωmax-ωmax)*(tmax-t)+ωmin是一个线性下降的惯性权重；c1，c2是学习因子。

为使获取测量的过程中减小测量噪声影响，提高UFK 估计的估计精度。以实测值和估计值之间的均方误差为目标函数构造适度函数。

通过最大化适应度函数Fm，可得到最优测量值，并得到最优误差ebest。利用差ebest对状态噪声协方差和观测噪声协方差进行估计［15］。观测噪声的协方差为

式中R0为观测噪声协方差的初始值；R(k)为看k时刻的观测噪声协方差。

状态噪声协方差的估计可用处理状态噪声协方差估计的方法进行计算，Q=qIn*nn 为预测空间的维数，估计公式为

其中，qth为阈值常数；Q0=q0In*n是状态噪声协方差初值；ΔQ为常量。

4 仿真分析

为了验证算法的性能引入均方根误差作为评价指标：

其中，yk，i是状态量的预测值的第i 个分量；ŷk，i是状态量的理论值的第i 个分量；N 是状态量的维数。该值越小，说明预测值越接近理论值。

含注入信号和谐波信号可描述为

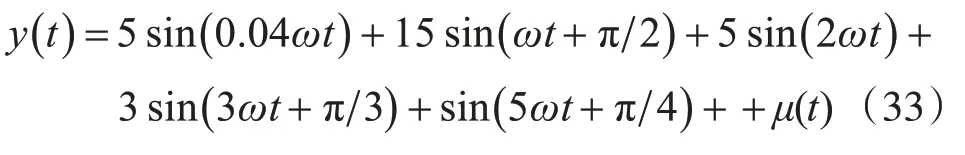
其中μ(t)表示均值为0，方差为0.05 的随机噪声。采样率fs=2.5kHz，采样间隔时间Δt=0.4ms。

图1（a）为2Hz信号注入的幅值的跟踪波形图，图1（b）稳定后2Hz 信号注入的幅值的RMSE 曲线图。从图1 中可以看出，在信噪比较低的情况下，POSUFK 得到的幅值曲线，与理论值基本重合，系统在一个周期达到稳定，但在系统稳定之前的性能比UFK差，但在稳定之后误差更小精度更高。

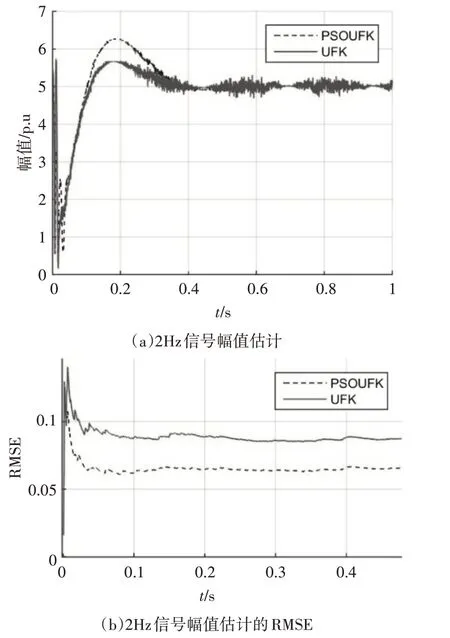
图1 2Hz信号的幅值估计

图2（a）为100Hz 信号注入的幅值的跟踪波形图，图2（b）为稳定后100Hz 信号注入的幅值的RMSE 曲线图。同样的从图2 中可以看出，系统在一到两个周期后达到稳定，在系统稳定之前的性能比UFK 差，但在稳定之后PSOUFK 对100Hz 信号的跟踪误差更小精度更高。

图2 100Hz信号的幅值估计

5 结语

本文通过粒子群优化无迹卡尔曼提高混频注入法的检测精度。通过仿真，粒子群优化无迹卡尔曼在系统稳定前没有优势，但在系统稳定后时具有更高的检测精度。在滤除稳定前的数据后能有效提高混频注入法的电流幅值的检测精度。