相似历史数据段高效查找方法研究*

庞向坤 高 嵩 张绪辉 颜 庆

（国网山东省电力公司电力科学研究院 济南 250002）

1 引言

随着新能源发电规模不断扩大，其间歇性、波动性等为电网稳定运行带来了日益严峻的挑战。由于火电机组实发功率具有高度的可调节性，其对电网多类型机组协调及稳定运行发挥日益突出的支撑作用。因此，提高火电机组的平稳运行水平，在一定意义上说就是保障新能源消纳，促进了电网多类型机组协调和稳定运行。

火电机组运行过程中，经常出现运行异常导致机组降负荷情况发生，降低了火电机组负荷调节能力。关于火电机组运行异常监控已经有众多的研究结果［1~5］，但在发现生产异常后，及时找出发现异常根源，提高异常处理效率，则是保障机组恢复生产能力的重要环节，目前相关研究结果较少。

当前，火力发电生产过程的信息化和智能化建设不断深入，海量生产过程数据被采集并存储。鉴于历史数据中包含有丰富的可用信息，因此，历史数据挖掘得到的信息，既可以用于火力发电过程管理与优化，也可以应用于火力发电过程监控等，对于提高火力发电生产效益和安全性等具有重要的意义，如文献［6~9］均从数据挖掘方法出发，来分析生产过程异常或故障原因。但是由于历史数据的维度急剧升高且受噪声影响，查找历史数据相似数据段主要面临查询效率不高和准确性较低的问题。

为了提高历史数据查询效率和准确性，近年来研发的技术方法主要是通过简化数据结构保留主要特征，实现降低原始数据维度的目的。文献［10］提出一种基于分段聚合近似（PAA）的时间序列早期分类方法，运用PAA 对时间序列样本进行维数约简。文献［11］提出了符号聚合近似转换（SAX）技术，主要是基于分段聚合近似（PAA）技术进行数据化简并离散化，将各个数据段用其均值表示，然后采用预设断点将PAA 系数转换为SAX 符号。文献［12］定义了极值噪声和转折点，在此基础上提出了基于转折点的分段线性表示方法。文献［13］提出了剪辑技术或定极限技术，实现对数据的压缩。文献［14］提出基于形态特征的时间序列符号聚合近似方法，综合考虑分段序列的均值和数据分布的形态特征，并且通过论域转化对它们实现符号转化。文献［15］针对PAA 算法对每一区间都平均对待所存在的不足，提出一种基于小波熵的时间序列分段聚合近似表示（PAA_WE）方法。

虽然上述方法均存在其应用场景，但是也存在一定的不足。例如，PAA技术虽然可以降低数据维度，但没有考虑数据段的趋势信息。在充分借鉴国内外现有相似数据段查找方法的基础上，本文采用了一种新型的数据表示方法，该方法将原历史数据转换为二进制表示形式，采用分段聚合近似（PAA）方法和扩展的剪辑技术合并了原历史数据的趋势和数值信息，实现了数据降维，提高了相似特征数据段查找效率和精度。

2 所提方法

本文以实现异常根源诊断为目的，充分利用所选取的目标数据集中各段数据的异常根源信息，当生产运行过程中异常状况出现时，通过查找当前异常数据段在目标数据集中的相似数据段，以其中的异常数据段为参考，确定当前运行异常的出现的根源。

2.1 时间序列的符号表示

本文采用了一种数据的二进制表示方法［16］，该方法是将给定的数据序列数据转换成长度为2ω的布尔符号表示序列，此处ω表示数据序列PAA的分段数。在布尔符号表示过程中，每一个PAA子段采用两位布尔数表示，其第一位布尔数值表示数据幅值信息，通过比较数据段前幅值与其均值得到；第二位布尔数值表示趋势信息，通过比较数据段前数值与最近点的位置得到。对历史运行数据X，以单步滑动窗口法得到X的子序列X[i]，然后采用PAA 方法对X[i]进行分段，对每个子数据段按如下方式进行其趋势和数值信息的符号转换［16］：

式（1）、（2）中，xˉk为时间序列X分段后第k子数据段的样本均值，Xˉi为X[i]的均值；式（3）中，xˉk+1为时间序列X分段后第k+1 个子数据段的样本均值，即xˉk+1=(xk+1+xk+2)/2。

数据二进制符号表示后，对以相应结果进行融合，数据幅值信息均以二进制序列奇数位表示，趋势信息均以二进制序列偶数位表示，X[i]对应的二进制序列以B[i]表示，B[i]={b(i·ω+1)，b(i·ω+2)，…，b(i·ω+ω)}，具体转换过程如图1示例。

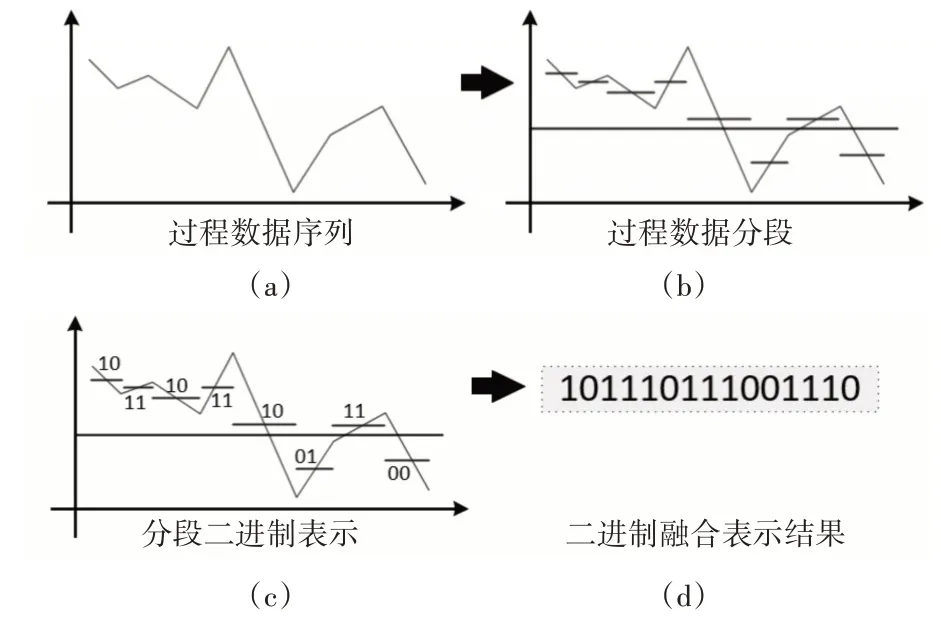
图1 数据序列转换为二进制序列过程示意图

2.2 形成目标数据集

完成二进制数据转换后，得到BC和B[i] ，i∈[1，N-1]，为了筛选出相关性较高的子数据段，可以指定相似性阈值ε，将BC和B[i]相似性大于阈值ε的子序列对应的X[i]提取出来，形成目标数据集。

二进制数据序列BC和B[i]的相似性采用符号相似系数度量，在此，BC={bc(1)，bc(2)，…，bc(ω)}，B[i]={b(i·ω+1)，b(i·ω+2)，…，b(i·ω+ω)}，其符号相关系数计算公式如下：

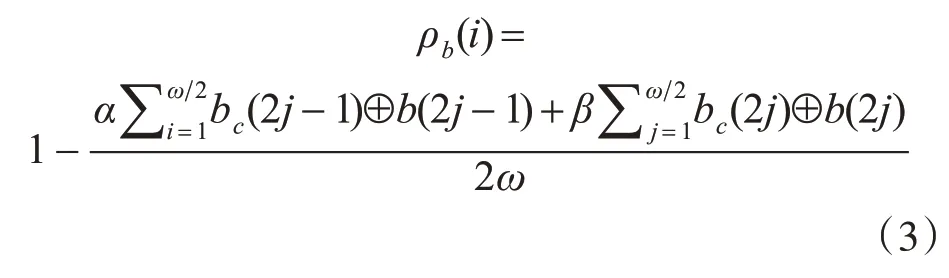
式（3）中，α和β分别是对数值信息和趋势信息所加的权重，满足0 ＜α，β＜1。α和β的取值可根据需要查找的异常数据段的特征进行选择。式（3）中，分子分别为二进制序列的奇数位和偶数位的汉明距离［17］。式（3）中，符号⊕表示布尔异或运算，且ρb的取值范围为[0，1]。

最后，将ρb(i)大于阈值ε的X[i]提取出来，设共有L组满足条件，则组成的时间序列候选集，候选集Cs中的数据维数将远小于，因此将大幅度缩小相似数据段查找范围，使得查找速度大幅提高。为了避免单步滑窗提取X[i]所带来的ρb(i)在X局部取过多较大值，造成候选数据集维数过高的问题，选取ρb(i)大于阈值ε时，应满足任意两个选定的相关系数ρb(i)和ρb(j)之间满足 ||i-j＞ω2。

2.3 确定相似异常数据段

采用二进制序列表示原数据，必然造成式（3）中的相似性计算结果较为宽泛，因此需要对候选集中数据进一步与当前异常数据进行相似性分析。

对Xl[i]={x(i·ω+1)，x(i·ω+2)，…，x(i·ω+ω)}，其与的皮尔逊相关系数计算公式如下：

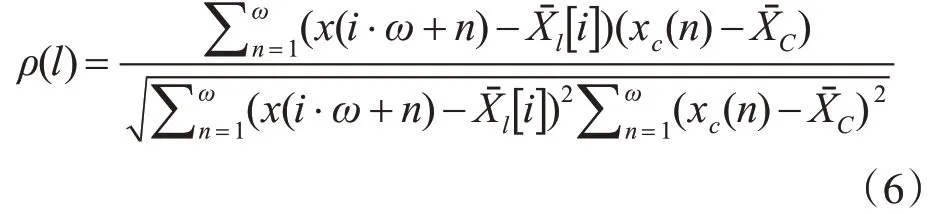
对于式（6）中得到的计算结果，按从大到小的顺序进行排序，相关系数越大则时间序列的相似程度越高，实现查找相似时间序列的目标。

3 仿真案例

为了验证所述方法的准确性和高效性，分别构造仿真案例予以说明。仿真过程中，采用MATLAB M语言实现该算法，使用的计算机中央处理器（CPU）为Intel 酷睿I5-4200M，主频2.5GHz（最大睿频3.1GHz），运行内存为4GB，操作系统为Windows 7 64位旗舰版。

3.1 准确性验证仿真

首先，构造子数据段长度和幅值随机的仿真数据，所构造数据的总长度为N=18000，数据趋势如图2 所示。将所构造的仿真数据看作是历史数据X，为了验证算法的有效性，以图2 中是红色数据段作为当前异常数据段XC，具体如图3所示，将两段绿色数据段设定为与红色数据段高度相似的数据段。

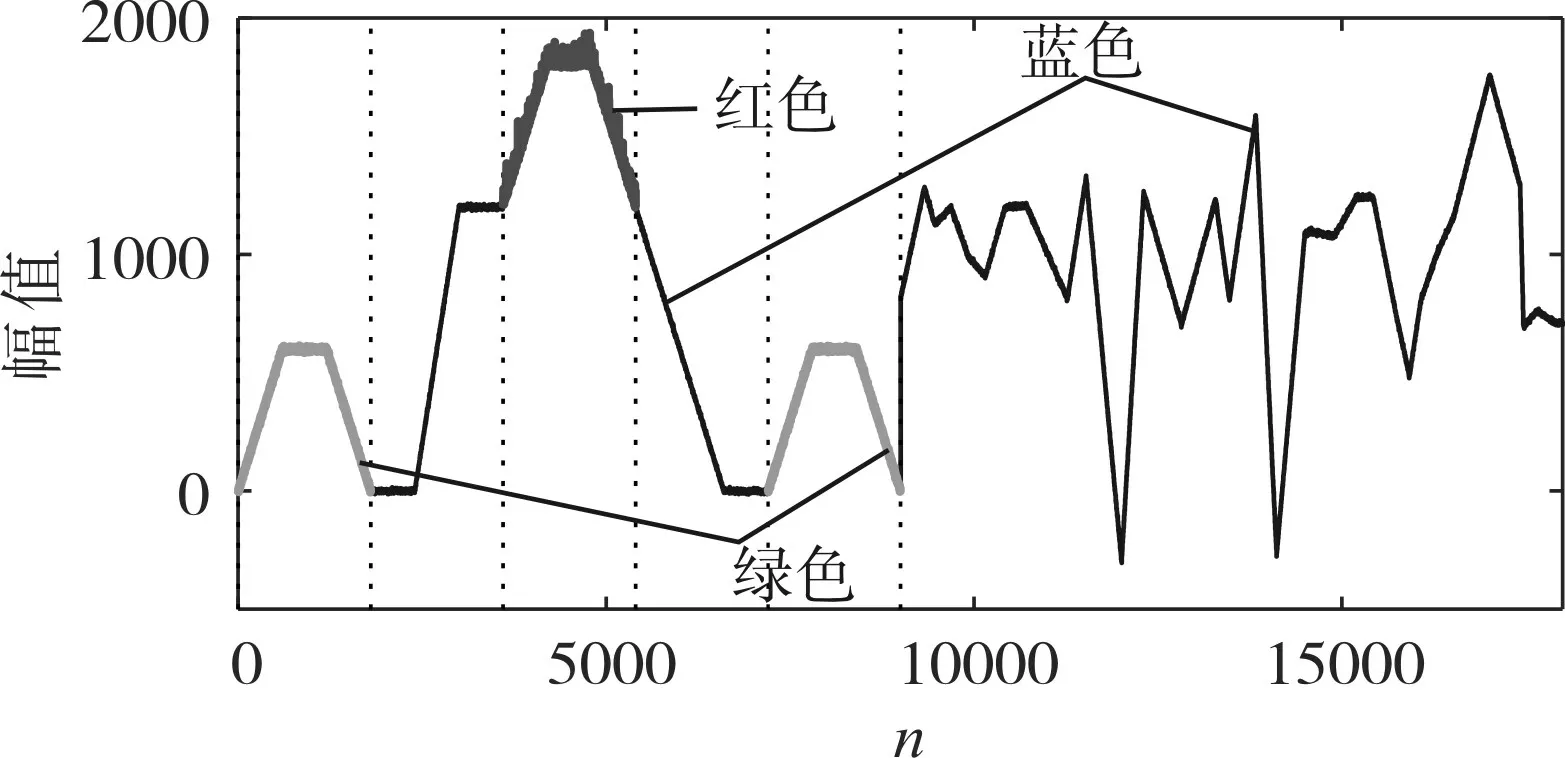
图2 所构造的仿真数据趋势曲线

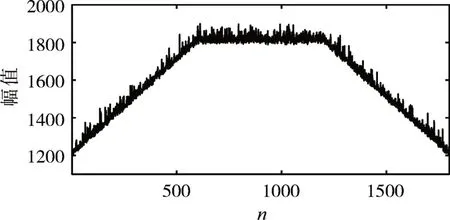
图3 当前仿真数据图

将仿真数据X与当前异常数据段XC二进制符号转换，根据式（2）和式（3）对每个子序列X[i]的数值信息和趋势信息分别进行符号转换后进行合并，得到BC和B[i]。根据式（3）计算每个序列对(BC，B[i])之间的相关系数ρb(i)，设ε=0.7，按照该阈值筛选二进制子序列。依据所选的二进制子序列，提取仿真数据X对应的数据段形成候选集Cs。

依据式（6）计算候选集Cs中每个子数据段与XC的皮尔逊相关系数，且设定皮尔逊相关系数的阈值为0.99，选出最终相似的时间序列对，并按相似性数值进行降序排列。在此，选择相似性最高的前三组作为最终选择的数据段，结果如图4 所示，其中图4（a）为当前异常数据段XC本身，即图2 中的红色数据段，图4（b）为图4中的第二个绿色数据段，图4（c）为图4中的第一个绿色数据段。

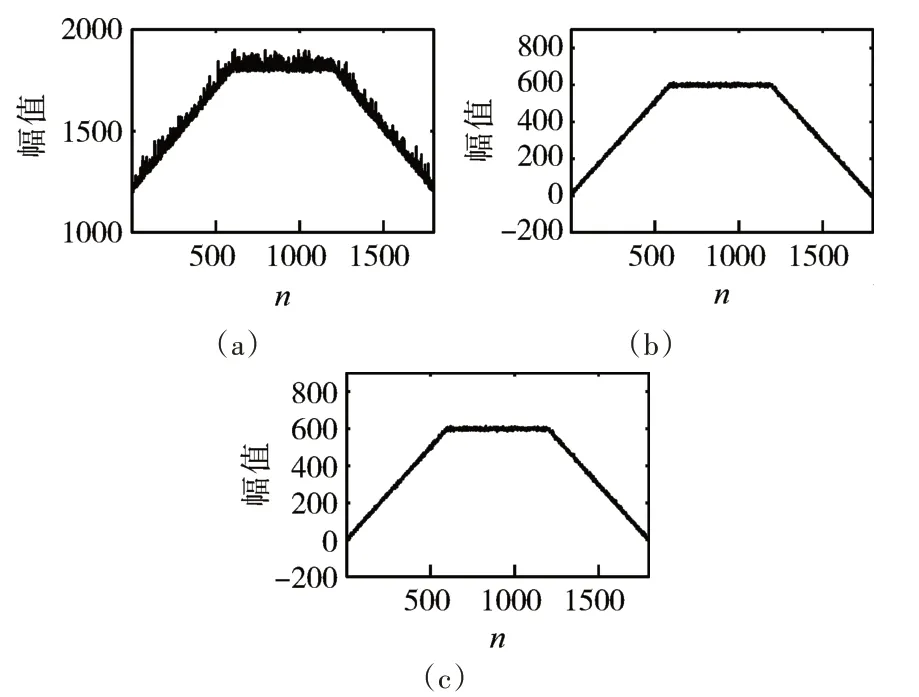
图4 结果集中的时间序列对

由本仿真案例所查找到的相似数据段和仿真数据段的设计结构可知，本文所述的方法能够准确查找出相似数据段。

3.2 高效性仿真验证

为了验证所述方法的高效性，在此通过构造不同长度的仿真数据，分别以本文所述方法和皮尔逊相关系数直接查找相似数据段方法做耗时对比验证，结果如表1所示。

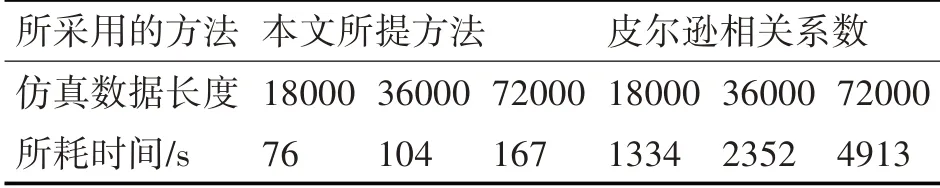
表1 所提方法与皮尔森相关系数的效率比较

通过对比仿真结果可知，在相同标准下，本文所述的方法在查询速度上有大幅度提高。

4 结语

当前新能源大规模并网条件下，电网需要在多类型机组协调下运行，火电机组对电网多类型机组协调发挥至关重要的作用。在该背景下，本文研究了用以机组运行异常根源诊断的历史数据相似数据段查找技术。通过计算当前异常数据段与原过程数据的二进制相似系数，形成目标数据集，进而通过皮尔逊相关系数查找目标数据集中与当前异常数据段高度相似的异常数据段，实现相似数据段查找的目的。通过仿真表明，该方法具有良好的准确性和高效性，对提火电机组运行水平以支撑电网多类型机组协调运行具有一定的意义。