考虑齿隙的多约束导引控制一体化设计方法

姜 尚, 魏 波, 梁伟阁, 孙东彦, 李进军, 马 野

(1. 海军大连舰艇学院导弹与舰炮系, 辽宁 大连 116018; 2. 海军工程大学兵器工程学院, 湖北 武汉 430033)

0 引 言

近年来,世界军事强国不断加快海军战略的转型改革,“从海到陆,由海制陆”等海战思想也在快步发展,都需要舰炮装备在对海对岸作战时,具备远程精确打击与持续火力支援能力。舰炮制导炮弹不仅比导弹射速高、效费比高、持续作战能力强,而且较常规弹药射程远、脱靶量小,能够对近岸目标实施远程压制与精确打击,为登陆部队提供持续可靠的火力支援。

导引控制系统是关系到舰炮制导炮弹实现作战目标的关键,它的常规设计方法是基于时标分离条件,忽略两子系统之间的耦合作用,难以证明整体制导系统的稳定性。但随着攻防装备升级、弹目相对运动加剧,质心导引与姿态控制之间的耦合作用显著增强,将两个子系统进行导引控制一体化(integrated guidance and control, IGC)设计,能够进一步提升制导系统的整体性能。

Williams等最早在1983年提出IGC,通过气动角来联系质心导引与姿态控制,集成出一个高阶串级系统,根据弹目相对运动、弹体姿态等信息直接解算出舵机的操纵指令。随着现代控制理论的蓬勃发展,涌现出最优控制、反步控制、动态面控制、滑模控制(sliding mode control, SMC)等IGC设计方法。

应用最优控制进行IGC设计的难点是求解Hamilton-Jacobi-Bellman方程,Vaddi等基于Riccati方程实现了IGC数值求解,但计算量大。Xin等基于θ-D方法成功地进行了IGC次优化设计,其性能却敏感于指标权重。针对飞行器IGC设计问题,Seyedipour等提出了一种反步控制方法,通过Lyapunov理论分析了系统稳定性。针对导弹IGC系统,Ibarrondo等基于反步控制完成了IGC设计,该方法的主要缺陷是,在解算虚拟控制量的时候容易造成微分膨胀问题。为此,Wang等在进行导弹纵平面IGC设计时,运用低通滤波器进行求解,有效地避免了微分膨胀现象的出现。Guo等针对拦截弹IGC设计中存在的喷流扰动,运用动态面控制有效减弱了控制量峰值。响应速度快、实践难度小、系统稳定性强等是SMC的显著优势,Jiang等基于一阶滑模提出了IGC设计方法,运用视线角与视线角速率构造滑模面。Koren等研究了导弹拦截机动目标时的IGC设计问题,提出了无需目标机动先验信息的一阶SMC方法,具有一定的实际应用潜力。Sagliano等基于高阶滑模设计了飞行器IGC控制指令,在一定程度上提升了制导系统的整体性能。同时,作用于系统内、外部的不确定性干扰,无疑对IGC设计施加了更多的压力。因此,Wang等运用扩张状态观测器(extended state observer, ESO)精确地估计出未知干扰,提高了IGC系统的鲁棒性。ESO由Han首次提出,可以迅速准确地观测出不确定性干扰，值得一提的是,它并不需要研究对象准确的数学模型。进一步地,Wang等将IGC设计转化为状态变量的跟踪问题,设计ESO估计目标机动,但未将ESO的观测误差纳入到系统稳定性分析当中。

在实际作战中,为了提升对目标的毁伤效果,往往会要求弹体以一定的攻击角命中目标;制导炮弹区别于导弹等的最大特征,就是发射后始终处于自旋状态,这限制了视线角速率的测量,上述约束条件显然向IGC设计提出了新的挑战,尤其是在同时还要兼顾系统一致最终有界(uniformly ultimately bounded, UUB),而这些恰恰是客观存在且亟待解决的重要问题。值得注意的是,相对于导弹等高速飞行器,制导炮弹只采用电动舵机作为唯一的执行机构,而齿隙是制约舵机性能的重要非线性因素,但在上述文献中,均是将舵机视为低阶的理想模型,难以反映出实际存在于舵机中的非线性特性与动态特性对飞行控制的影响程度,因此在设计IGC方法时考虑舵机齿隙具有重要的意义。

然而,齿隙死区模型具有非连续、不可微等非线性特性,并且重要的参数通常也很难精确测量出来,这在一定程度上阻碍了齿隙模型建立与精确补偿控制,于是诸多学者先后提出了包括逆模型、迟滞模型等在内的一些齿隙非线性模型。但是在舵机三闭环控制系统中,齿隙很难直接折算到控制指令的输入端,这限制了逆模型的推广与应用,另一方面,迟滞模型虽然具有结构简单的优势,但它是不可微的,容易导致传动力矩在换向时发生震荡。为了能够对其进行高精度的逼近,文献[30]设计了一种便于系统控制的近似死区模型,它具有连续可微的性质,文献[31]进一步阐明了采用该模型描述齿隙的合理性与可行性,并分析论证了参数选取与逼近精度的关系。

本文综合考虑了多项约束与齿隙因素,基于动态面滑模(dynamic surface sliding mode, DSSM)控制与Lyapunov稳定性理论,提出了考虑齿隙的多约束导引控制一体化(IGC with multiple constraints and backlash， IGCMCB)方法。需要解决下列几项问题:首先,针对不确定干扰与视线角速率难以测量,要设计ESO对其进行实施准确迅速的观测,并将观测误差纳入到系统稳定性分析中;然后,为了在有限时间内零化视线角跟踪误差与视线角速率,需要结合弹目距离与接近速率,设计具有自适应指数趋近律的非奇异终端滑模,并且运用DSSM消除控制量的高频抖振;最后,IGCMCB不仅需要使制导炮弹满足多项约束条件和全系统状态UUB,同时也应该有效地削弱齿隙对于IGC设计的影响。

1 模型建立

1.1 IGC设计模型

在纵平面中,构建制导炮弹IGC设计模型,示意如图1所示。

图1 制导炮弹的IGC设计模型Fig.1 IGC design model of guided projectile

图1中,表示舰炮制导炮弹,为目标,、、、、、分别为基准系、弹体系、弹道系、视线系、目标基准系、目标弹道系,、与、表示弹体和目标的速度、弹道倾角,、、、、、分别表示弹目距离、视线角、俯仰角、攻角、舵偏角、水平风速,2、2表示弹体加速度在系的分量,8、8表示目标加速度在系的分量。为便于分析讨论,作以下合理假设:

视目标为质点,、、均易通过成熟途径获取,且始终满足>。

弹目相对运动关系为

(1)

式中:=-；=-；为目标机动引入的干扰；2、2分别表示为

(2)

在纵平面内,弹体动力学方程为

(3)

式中:、表示俯仰力矩、转动惯量,其中,为

(4)

升力主要由产生,将由产生的升力视为有界不确定干扰。

根据文献[14],可以将攻击角视为在弹体命中目标时,弹体速度与目标速度之间的夹角,并且约束可以等价地转换为对的终端值的约束。

1.2 含齿隙的双惯量舵机模型

图2 含齿隙的舵机双惯量模型Fig.2 Double inertia model of canard with backlash

该模型可由如下传动力矩方程描述:

(5)

式中:=max为铰链矩系数,max为舵机最大力矩;=-为驱动、从动轴之间的相对转角,即齿隙宽度,且有-2≤≤2;()为连续不可微的死区函数。为了便于设计,引入连续可微的近似死区函数:

(6)

记()与()的逼近误差为Δ()。

弹载舵机的电机伺服系统采用三闭环控制方式,同时,引入含有非线性齿隙的舵机双惯量模型,记、、分别表示电流、速度、逆变器的比例控制系数,为位置控制器输出的控制信号,为速度环反馈系数。

1.3 近岸目标模型

近岸目标可以由一阶惯性环节描述:

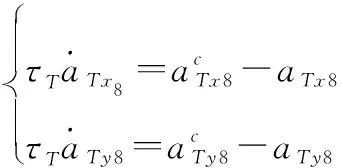
(7)

1.4 系统状态空间模型

(8)

式中:=e-(1-e-)(1+e-)；=1-2e-(1+e-)。为了便于分析讨论,根据系统实际情况,作合理假设如下:

Δ()在定义域上属于连续函数,当且仅当=±时不可导,原因是左导数不等于右导数,但在除此以外的定义域上,均可导,并且导数有界。

2 IGCMCB设计

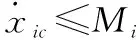
设计方法目的为针对含舵机齿隙双惯量模型的IGC系统式(8),在约束、测量受限、(=2,3,4,6,8)未知有界的工况下,得到适宜的控制量,在有限时间内零化、,确保系统UUB,迅速稳定地收敛至平衡点附近充分小的邻域内。

设计方法IGCMCB结构原理如图3所示,主要由ESO、非奇异终端滑模(nonsingular terminal sliding mode, NTSM)与DSSM等构成,现分别对它们进行设计,随后再进行闭环系统的稳定性分析。

图3 IGCMCB的结构原理示意图Fig.3 Schematic diagram of IGCMCB structure and principle

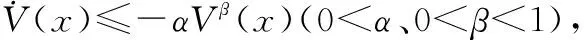
2.1 ESO设计

(9)

式中:0<<<；0<<<1；0<2<1(=1,2)；非线性函数fal为

(10)

进一步化简式(9),可得观测误差的动态方程组为

(11)

式中:fal为分段非线性函数,显然需要分情况进行讨论,当<|21|时,有等式fal(21,,)=|21|sign(21)成立,结合等式21=|21|(1-)|21|sign(21),式(11)可化简为

(12)

(13)

(14)

(15)

证毕

为了迅速准确地观测出不确定性干扰(=3,4,6,8),定义观测变量、,定义观测误差为1=-、2=-,分别设计二阶ESO为

(16)

式中:各参数定义、取值范围以及函数形式参照ESO模型式(9)。

2.2 NTSM设计

为保证系统状态收敛的快速性,同时避免奇异问题出现,设计NTSM为

=+||sign(), 0<；1<<2

(17)

对式(17)求导可得

(18)

(19)

联立式(8)和式(9),并舍弃奇异因子||(1-)(),推导虚拟控制量3为

(20)

针对系统式(8)前两个等式构成的子系统,采用ESO模型式(9)与NTSM模型式(17)和式(19),通过选择合适的参数,则能使系统状态、在有限时间内收敛至零。

(21)

(22)

根据引理2,、可以在有限时间内收敛至零。

证毕

2.3 DSSM设计

系统式(8)属于高阶非线性系统,为了对其进行有效的镇定,并且避免反步法产生的微分膨胀问题,需要运用DSSM进行方法设计。

设计3使→0,通过一阶滤波器得到3,其有时间常数:

(23)

定义动态面3为=-3,求导可得

(24)

设计DSSM的指数趋近律为

(25)

同理,设计动态面4～8分别为

=-，=4,5，…,8

(26)

式中:为虚拟控制量的滤波值,设计与控制量分别为

(27)

式中:|1|≤(=3,4,6,8),0≤,0≤,0<(=3,4，…,8),为避免对(=3,4，…,8)直接求导而产生微分膨胀问题,设计一阶滤波器为

(28)

至此,IGCMCB设计完毕,由ESO模型式(9)和式(16),NTSM模型式(17)和式(20),DSSM模型式(23)～式(28)组成。

IGCMCB中的(=2,3,…,8)为滑模切换项增益,与其对应的符号函数共同组成滑模切换项,作用是抑制不确定干扰并保证系统快速稳定,而||(2-)()虽然也带有符号项,但它仅仅是由NTSM引入的附加切换项。

3 稳定性分析

定义虚拟控制量误差为

=-，=3,4，…,8

(29)

进行求导,可得

(30)

进一步推导,可得

(31)

=++

(32)

选取闭环系统Lyapunov函数为

(33)

对于系统式(8),采用IGCMCB设计方法,通过选择合适的参数,则能够使闭环系统UUB,并且能够迅速稳定地收敛至平衡点附近充分小的邻域内。

对全系统Lyapunov函数式(33)进行求导,并结合上述分析,推导可得

(34)

为了保证系统稳定,在选取参数时需要满足以下条件:

(35)

令正常数=min{(=1,2,…,13)},则式(34)可以进一步化简为

(36)

(37)

证毕

尽管式(35)给出了保证系统稳定性的参数选取范围,但由于受到多方面因素的约束,例如,在提高系统收敛速度的同时,需用过载往往容易超过可用过载,因此给出设计参数的具体定量选择标准是比较困难的。目前常采用的方法是综合考虑设计方法与实际物理环境,再通过大量的数学仿真来进行定量选择。

为了便于定理3的推导证明,在中并未包含ESO模型式(9)和式(16)的观测误差项,但结合定理1可知,当中涵盖这些ESO观测误差项时,定理3是同样成立的。

4 仿真实验

本节的主要目的是分别在目标固定与蛇形机动的工况下,通过数学仿真对IGCMCB进行分析与验证。微分方程组解算方法采用4阶Runge-Kutta,步长10 ms。仿真环境、弹体、舵机以及IGCMCB的参数设置分别如表1～表4所示。

表1 仿真环境参数Table 1 Simulation environment parameters

表2 弹体参数Table 2 Projectile parameters

表3 舵机参数Table 3 Canard parameters

表4 IGCMCB参数Table 4 IGCMCB parameters

表1～表3中下标“0”表示参数初值。根据在第1节中建立的设计模型可知,、2、2、等是由其他已定义变量构成的,因此仅需要给出Δ2、Δ2、Δ、、等项的数值,以便于定量分析干扰项。

为了探究舵机齿隙对于IGC设计的影响,同时又能够体现出IGCMCB抑制齿隙的有效性,引入自适应动态面控制(adaptive dynamic surface control, ADSC)作为对比,含齿隙舵机部分采用PID控制,简记为ADSC&PID。

4.1 工况1:固定目标

表5 工况1的仿真实验结果Table 5 Simulation results of condition 1

图4 工况1仿真实验曲线Fig.4 Simulation curves of operating condition 1

4.2 工况2:蛇形机动目标

表6 工况2的仿真实验结果Table 6 Simulation results of condition 2

图5 工况2仿真实验曲线Fig.5 Simulation curves of operating condition 2

5 结 论

针对舰炮制导炮弹在实施对岸远程火力支援的末段,考虑齿隙、约束攻击角以及测量视线角速率受限,基于DSSM与ESO设计了IGCMCB,主要从构建模型、方法设计、系统稳定性分析以及仿真实验等4个方面展开了详细的研究,现总结全文如下:首先,设计了ESO准确迅速地估计出视线角速率与各类干扰,分析了由观测误差所组成系统的稳定性,为导引控制提供了关键必要信息;然后,结合弹目距离与接近速率,设计了具备自适应指数趋近律的NTSM,在有限时间内零化了视线角跟踪误差与视线角速率,运用DSSM成功地避免了控制量高频抖振;最后,IGCMCB使制导炮弹在满足多项约束和系统UUB的同时,有效地削弱了齿隙对IGC设计的影响,所需信息均可通过成熟技术途径获取,具有一定的理论意义与应用价值。