考虑合成机制的多星应急任务调度

靳 鹏, 唐晓茜,*

(1. 合肥工业大学管理学院, 安徽 合肥 230009; 2. 过程优化与智能决策教育部重点实验室, 安徽 合肥 230009)

0 引 言

对地观测卫星是空间范围内的一种成像资源,根据用户对地球表面目标的成像需求,利用星载传感器,在满足卫星成像的约束条件下,对地球表面目标进行观测,获取图像信息。由于具有成像效果好、覆盖区域广且不受国界限制等优点,在环境监测、资源探测、灾害预警、军事侦探等领域发挥着重要作用。当地震、火灾等紧急情况发生时,充分利用卫星资源对受灾区域成像已经成为一种获取图像信息的重要手段,能够为救援部门提供重要的决策信息支持。应急任务的观测会对原调度序列产生影响,如何设计高效的卫星应急任务调度方法,在保证观测总收益的基础上最小化对原调度序列的扰动是多星应急任务调度领域急需解决的问题。

应急任务具有两大特点:① 及时性,希望任务越早成像越好。应急任务的到达伴随着期望完成时间,但当任务实际完成时间比期望完成时间晚时,所获得的图像信息仍然有价值;② 随机性,任务到达的时间和数量是不确定的。在轨卫星成像过程中存在卫星状态改变、云层影响或用户需求转变等多种不确定性,导致用户提交的应急任务呈现随机性特点。虽然应急任务的到达是随机的,但调度任务并给卫星上注观测指令是统一完成的。本文在任务统一调度情况下研究多星应急任务调度问题。

卫星对任务观测成像需要满足时间窗、姿态转换时间、存储限制等多方面约束。近年来,用户的观测需求量持续上涨,远大于卫星资源负载能力,星上任务呈现饱和状态。在尽量减少对初始调度序列扰动的情况下完成应急任务调度变得更加复杂。

目前,国内外学者已经对多星应急任务调度问题展开大量研究。文献[14-20]采用蚁群算法、局部迭代搜索算法、粒子群算法和遗传算法等启发式算法完成应急任务调度。文献[21]以最大化任务观测收益和数量为目标,提出直接插入或删除插入(insert directly or insert by deleting,IDI)算法和直接插入、移位插入、删除插入和被删除任务重插入(insert directly, insert by shifting, insert by deleting, and reinsert the tasks deleted, ISDR)算法完成应急任务调度。文献[22]以任务调度总权重最大和应急任务提前完成时间最长为目标,在ISDR算法的基础上加入回溯算子,设计插入、移位、回溯、删除和重插入(insertion, shifting, backtracking, deletion, and reinsertion,ISBDR)算法解决问题。两种算法都以移位、重插入的方式处理常规任务,但都未考虑对初始调度序列的扰动情况。另外,上述文献并未突出应急任务完成时间对观测收益的影响,认为应急任务的观测收益恒定不变。

现实中资源有限、任务繁多，任务以最佳侧摆角独立观测时完成率低且资源利用不充分。因此,学者采用任务合成机制增大任务观测数量和收益,提高卫星资源利用率。文献[23-27]建立合成任务的调度模型,以最大化任务观测收益为目标,采用模拟退火算法、蚁群算法和动态规划算法等启发式算法完成合成任务调度。文献[28-30]应用最小派系划分思想实现任务合成,基于图论建立模型,设计启发式算法求解问题。文献[31]设计启发式规则实现任务合成与动态调度,但未建立相关模型。上述文献都是在常规任务间执行任务合成,并未考虑对应急任务的合成操作。

应用任务合成机制处理应急任务的研究较少。文献[7]侧重于对应急任务合成位置选择的研究,不存在整体寻优过程。文献[32-34] 考虑应急任务与常规任务合成的同时以最大化任务观测收益和最小化序列扰动为目标,设计启发式算法完成应急任务的动态调度。这对原来任务序列的鲁棒性要求较高,调度难度也较大。

本文综合考虑应急任务完成时间和观测收益指标,建立有时间依赖性收益的数学规划模型。将合成机制与遗传算法融合解决多星应急任务调度问题,提出考虑合成机制的多星应急任务调度算法(genetic algorithm with task merging for emergency task scheduling,GA-TM-ETS)。算法以应急任务优先调度为原则,首先设计任务合成、插入、替换等3种算子完成向初始调度序列添加应急任务的操作;其次考虑任务观测收益、序列扰动和最短观测时间等因素设计适应度函数,提高算法搜索速度;最后设计基于组基因的交叉算子和变异算子,结合全局修复算子进行序列寻优。实验表明所设计的GA-TM-ETS算法能够显著提高调度质量,适用于多对地观测卫星应急任务调度。

1 问题描述

对地观测卫星应急任务调度问题有以下描述。

给定一组卫星,在调度周期内存在轨道集合={,,…,,…,||},||为轨道数量。

本文以轨道作为资源的最小调度单元,任一卫星轨道圈次的属性可以用六元组<,span,,,,>表示。其中,表示轨道上传感器视场角,span表示传感器最长开机时间,表示传感器单位时间成像的存储系数,表示轨道最大存储量,表示传感器偏转速率,表示传感器姿态稳定时间。

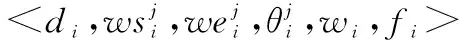
1.1 任务合成

卫星以一定侧摆角和时间窗对任务观测成像时形成观测条带。在一个观测条带内,满足某种约束条件下,将多个地理位置相近的任务同时观测的过程为任务的合成观测。如图1所示,应急任务和常规任务′满足卫星侧摆角约束和传感器单次最长开机时间约束,可以在卫星的一个观测条带内合成观测。

图1 任务合成图Fig.1 Diagram of task merging

111 侧摆角约束

(1)

图2 侧摆角约束Fig.2 Swing angle constraint

(2)

112 单次最长开机时间约束

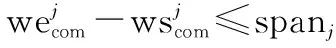
(3)

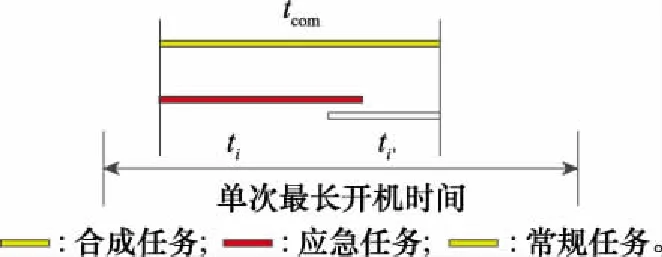
图3 最长开机时间约束Fig.3 Maximum boot time constraint

如图4所示,应急任务和常规任务′满足任务合成条件,且合成任务与前后在轨任务满足时间窗约束和姿态转换约束,则任务以任务合成方式执行观测。

图4 任务合成Fig.4 Task merging

1.2 任务插入

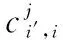
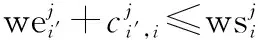
(4)

(5)

如图5所示,常规任务′和′+1之间存在足够长的空闲时间片段,应急任务满足任务插入式(4)和式(5),将其插入观测。

图5 任务插入Fig.5 Task insertion

1.3 任务替换

(6)

(7)

如图6所示,任务满足替换在轨任务′的式(6)和式(7),用替换′执行观测。

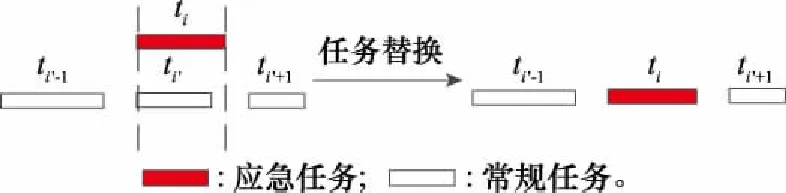
图6 任务替换Fig.6 Task replacement

2 调度模型

2.1 完成时间-收益函数

(8)

图7 应急任务完成时间-收益Fig.7 Emergency task completion time-revenue

2.2 扰动

应急任务的插入可能会扰乱初始调度序列。本文对初始调度序列上的常规任务设计了两种处理方式:删除任务或更换任务执行位置。设(=1,2)为任务第种处理方式的影响权重,当删除任务时取1,当更换任务执行位置时取2,并且>。

考虑常规任务调度序列Seq,应急任务插入后,轨道上的扰动表示为

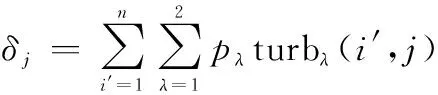
(9)

其中,turb(′,)定义为

(10)

2.3 数学规划模型

数学规划模型以合成任务为描述对象。设任务集={,,…,},为待观测的合成任务数量。当待观测任务中只包含一个元任务时,该任务也被看作合成任务。

231目标函数

本文的调度目标优先考虑最大化任务观测总收益:

(11)

(12)

另一个调度目标考虑对原任务调度序列扰动最小:

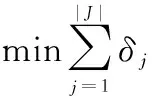
(13)

232 约束条件

每个任务只能被观测一次:

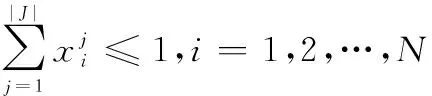
(14)

任务的观测结束时间一定不小于任务观测开始时间:

(15)

两连续观测任务间的时间间隔至少满足姿态转换时间约束,其中,是一个很大的正数:

=1,2,…,-1；=1,2,…,||

(16)

应急任务观测完成时间具体表示为

(17)

轨道上任务成像的存储空间不能超过单轨最大存储限制:

(18)

因此,多星应急任务调度问题可表示为上述具有时间依赖性收益的数学规划模型。

3 算法设计

遗传算法是基于自然选择和生物进化理论的演化算法,因其具有较强的广域搜索能力而被广泛应用于解决组合优化问题。本文以遗传算法为基础设计GA-TM-ETS算法求解问题。以应急任务优先调度为原则,首先,设计任务合成、插入和替换算子完成应急任务向常规调度序列的插入过程;其次,考虑任务观测收益、序列扰动和最短观测时间等因素设计适应度函数,提高算法搜索速度;最后,根据编码方式,设计基于组基因的交叉算子和变异算子,结合全局修复算子完成序列寻优。

3.1 编码方式

本文采用十进制的编码方式,以轨道为单元构造组基因,用组基因矩阵表示任务调度方案。

首先在调度周期内为卫星划分轨道并编号,每个轨道编号后存放在该轨道上执行的任务序列,每条轨道及其任务序列组成一个组基因。所有组基因组成组基因矩阵,一个组基因矩阵代表一个完整的卫星调度方案。如图8所示,调度周期内卫星共存在条轨道,在轨道2上最先执行任务16,最后执行任务47;在轨道上依次执行任务18、任务19和任务39。

图8 编码方式Fig.8 Encoding method

3.2 任务急切度

定义任务急切度确定应急任务安排顺序。

急切度

应急任务的急切度urg反映任务等待观测的迫切程度。使用任务观测收益和从调度时刻开始到期望完成时间之内的时间窗数量衡量任务急切度,表示为

urg=TWF

(19)

其中,TWF为任务从调度时刻开始到期望完成时间之间的时间窗数量。在应急任务调度过程中,更倾向于优先调度收益更大或时间窗数量更少的任务。

3.3 任务合成算子

应急任务首先以任务合成的方式完成调度。任务合成算子操作步骤如下:

根据应急任务在各轨道上的观测机会,将对有时间窗的轨道放入的候选轨道集COS中;

在COS中的轨道上确定能够与合成观测的在轨任务,获得任务的候选合成任务集CMTS;

若CMTS不为空,转步骤4;若为空,转步骤6,考虑任务插入算子;

从CMTS中随机选择并删除任务,将选中常规任务与应急任务执行合成操作,获得合成任务;

判断与在轨任务的冲突情况。若与前后任务不存在冲突,则直接将以任务合成方式插入;若存在冲突且冲突任务为常规任务时,将常规任务删除后合成,更新调度序列;若存在冲突且冲突任务为应急任务,不执行合成,转步骤3;

任务合成算子操作终止。

3.4 任务插入算子

当任务不能以合成方式插入时,利用任务插入算子完成调度。任务插入算子操作步骤如下：

在COS中的各个轨道中根据任务时间窗确定任务的可插入位置,获得候选插入任务集CITS;

若CITS不为空,转步骤3;若为空,转步骤5,考虑任务替换算子;

从CITS中随机选择并删除任务,执行任务插入操作,转步骤4;

判断与在轨任务的冲突情况。若与前后任务不存在冲突,则直接将插入;若存在冲突且冲突任务为常规任务,将常规任务删除后再插入,并更新调度序列;若存在冲突且冲突任务为应急任务,不执行插入,转步骤2;

任务插入算子操作终止。

3.5 任务替换算子

当任务合成算子和任务插入算子不能完成任务调度时,考虑任务替换算子。任务替换的目的是完成观测收益更高的任务,被替换的任务暂时存放到该染色体的未完成任务集(unscheduled tasks list, UTL)中,等待重插入。任务替换算子操作步骤如下:

从COS中随机选择并删除可观测任务的轨道,执行任务替换,转步骤2;

判断与在轨任务的冲突情况。若与前后任务不存在冲突,则直接将以任务替换方式插入;若存在冲突且冲突任务为常规任务时,将常规任务删除后替换,并更新调度序列;若存在冲突且冲突任务为应急任务,不执行替换;

任务替换算子操作终止。

3.6 适应度函数

遗传算法中种群个体的优劣由适应度衡量。本文联合任务观测收益、序列扰动和最短观测时间3个指标构造适应度函数,评判个体优劣。为说明最短观测时间指标,定义无效观测和有效重复观测。

无效观测

任务合成观测时,各元任务时间窗间可能存在时间间隔。执行观测时,传感器在该时间间隔内成像并存储数据,产生无效观测,如图9所示。

图9 无效观测Fig.9 Ineffective observation

有效重复观测

任务合成观测时,各元任务的时间窗间可能存在重叠。执行观测时,卫星一次扫描可以完成对多个元任务片段的观测,最大化利用卫星资源,产生有效重复观测,如图10所示。

图10 有效重复观测Fig.10 Effective repeated observation

当任务合成观测时,应急任务对合成位置的选择会直接影响卫星的成像时长。如图11所示,应急任务可以和轨道上的任务或轨道上的任务合成观测,合成后任务的观测时长分别为和。因为<,则选择与任务合成,在最短观测时间内执行观测,从而最小化无效观测,最大化有效重复观测,充分利用卫星资源。

图11 最短观测时间说明图Fig.11 Diagram of minimum observation time

综上,适应度函数设置下式所示：

Fitness=

(20)

两条染色体比较时,总观测时间更短,序列扰动更小,观测总收益更大的染色体序列更优。

3.7 交叉算子

针对本文的编码方式,设计组基因片段单点交叉方式执行染色体交叉操作。交叉策略是将选中的两条父代染色体根据随机选择的轨道编号分为两部分,交换后半部分组基因矩阵片段后删除重复任务,并执行任务重插入操作,获得子代染色体，如图12所示。

图12 染色体交叉Fig.12 Chromosome crossover

具体交叉步骤如下:

计算种群中各染色体的适应度值,将种群中染色体根据适应度值非升序排序,更新种群中染色体顺序;

从种群的前半部分随机选取待交叉的父代染色体F1,从整体种群中随机选取待交叉的父代染色体F2;

随机生成轨道编号;

以轨道为分割点,将F1分为矩阵片段F11和F12,将F2分为矩阵片段F21和F22;

在矩阵片段F22中删除F11中已存在的任务,在F12中删除F21中已存在的任务;

依次拼接矩阵片段F11和F22,获得子代染色体z1;依次拼接矩阵片段F21和F12,获得子代染色体z2;

从z1、z2的UTL中分别向染色体z1、z2中重新插入任务,最终获得子代染色体Z1、Z2;

采用精英策略从四条染色体F1、F2、Z1、Z2中选择适应度函数较小的两条染色体放回种群中。

3.8 变异算子

基于轨道组基因设计变异算子。随机选择轨道圈次,将该圈次的任务进行变异。变异策略是将选中组基因上的所有任务重新放入该染色体的UTL中,与未完成任务一起重新插入,如图13所示。

图13 染色体变异Fig.13 Chromosome mutation

具体变异步骤如下:

在种群中随机选取染色体F,在F中确定变异轨道编号;

将选中轨道上的任务放至该染色体的UTL中,清空选中轨道;

从UTL中向染色体中重新插入任务,获得子代染色体Z;

采用精英策略从两条染色体F和Z中选择适应度函数较小的染色体放回种群中。

3.9 全局修复算子

前面任务的调度过程主要考虑各任务间时间窗的冲突关系,并未根据卫星轨道的全局约束对任务分配进行限制,可能存在不符合轨道存储限制的不可行解。全局修复算子考虑卫星轨道整体约束,最终寻找最优解时,当在轨任务与轨道最大存储限制出现冲突时,优先删除具有更小收益的常规任务来消除冲突。

3.10 算法主要流程

GA-TM-ETS算法主要由初始种群的生成和种群序列寻优两部分组成。

3.10.1 初始种群生成

应用任务合成、插入和替换算子将集合TE中的任务插入到初始调度序列可得到染色体,重复此过程即可获得初始种群population。设初始种群数量为pop,初始调度序列为Seq。初始种群生成的算法如算法1所示。

初始种群生成算法

1 Initialize the set TE,pop,Seq;

2 Set popnum=1;

3 Calculateurgfor∈TE and sort TE by it from high to low;

4 for popnum=1 to pop do

5 for eachin TE do

6 ifand′in Seq satisfy the constraints (1)～(3) then

7 Merge task by task merging operator;

8 else ifand′in Seq satisfy

the constraints (4) and (5) then

9 Insert task by task insertion operator;

10 else ifand′in Seq satisfy the constraints (6) and (7) then

11 Replace task by task replacement operator;

12 end if

13 end for

14 end for

3.10.2 种群序列寻优

初始种群经过交叉变异寻优和全局修复算子修复过程获得最终调度序列Chromosome*。设种群最大迭代次数为maxiter,种群序列寻优的算法如算法2所示。

种群序列寻优算法

1 Initialize the set population;

2 Set iter=0;

3 for iter=0 to maxiter do

4 Cross by crossover operator;

5 Mutate by mutation operator;

6 iter++;

7 end for

8 Repair by global repair operator;

9 Select and return Chromosome*

4 仿真实验

本节通过对比实验验证GA-TM-ETS算法的有效性。实验在Intel(R) Core(TM) i5-6500CPU处理器、16.0G内存、64 位 Windows7 环境运行,基于myeclipse2017编程环境采用java语言实现。

实验中,初始调度序列采用遗传算法生成。实验利用仿真软件模拟真实环境生成3颗卫星,调度周期为24小时,卫星参数设置如表1所示。随机生成100、200、400个常规任务集合和20、40、60个应急任务集合,常规任务观测收益在区间[0，1]内随机生成,应急任务观测收益在区间[1，2]内随机生成。为避免数据偶然性,每种数据规模下分别对应生成3组数据执行实验,每组数据算例运行30次并取平均值作为该组数据实验结果,每种规模下的3个数据实验结果取平均值得到最终该规模实验结果,最终得到9组实验。

表1 卫星参数信息Table 1 Satellite parameter information

由于多星调度问题的多变性和复杂性,各个科研团体在考虑不同的实际应用下进行研究,目前在该领域没有公认的benchmark测试集。为验证算法的有效性,本文进行3组对比实验。首先,将不考虑合成机制的应急任务调度算法(genetic algorithm for emergency task scheduling,GA-ETS)与IDI算法对比,验证本文设计的基础算法的有效性;其次,将GA-TM-ETS算法和GA-ETS算法对比,证明合成策略在算法中的重要作用;最后,进行参数敏感性分析,确定各规模实验中各参数值的最优组合。

4.1 算法有效性实验

GA-ETS算法和IDI算法的共同点在于,两算法中都不存在合成机制。为验证基础的GA-ETS算法的有效性,将GA-ETS算法和IDI算法对比,实验结果如表2及图14所示。

为使IDI算法更加适用于本文的研究背景,将算法做出如下修改:将卫星对任务的可见时间窗作为观测时间窗,将应急任务根据优先级非降序排序并依次选择任务,遍历选中任务的时间窗,插入任务。

表2 GA-ETS算法和IDI算法结果Table 2 Results of GA-ETS algorithm and IDI algorithm

通过分析表2中两算法收益列和图14(a)可知,当常规任务规模分别为100、200、400时,随着应急任务规模的增加,GA-ETS算法和IDI算法的观测总收益都逐渐增加,且变化趋势相同,说明GA-ETS算法作为GA-TM-ETS算法的基础设计算法是有效的。表2最后一栏表示收益差值相对值,其计算公式为:收益差值相对值=(GA-ETS观测收益-IDI观测收益)/IDI观测收益。依据计算结果可知,常规任务规模为100时,应急任务规模为20、40、60情况下GA-ETS算法的观测收益比IDI算法分别提高12.57%、14.03%、14.30%,最高提高14.30%;常规任务规模为200时,应急任务规模为20情况下GA-ETS算法的观测收益比IDI算法提高最多,最高提高10.41%;常规任务规模为400时,应急任务规模为20的情况下GA-ETS算法的观测收益比IDI算法提高最多,最高提高9.55%。实验结果表明GA-ETS算法优于IDI算法。

图14 GA-ETS算法和IDI算法实验结果对比Fig.14 Comparison of the experimental results of GA-ETS algorithm and IDI algorithm

扰动度量时,分别将任务删除和任务移位的干扰量设置为1和0.5。根据表2中两算法扰动列和图14(b)分析可得, GA-ETS算法的调度扰动量不小于IDI算法,但扰动差值在区间(0,5.5)之内。在GA-ETS算法的观测收益明显大于IDI算法的条件下,扰动量的少量增加是可以接受的。

分析表2中两算法运行时间列可知,IDI算法运行很快,大规模实验下完成调度仅需约20 s。GA-ETS算法的交叉变异过程需要判断各任务时间窗之间的冲突,消耗一定的时间成本,运行相对较慢,大规模实验下完成调度需82.190 s。但在GA-ETS算法的观测收益明显大于IDI算法的条件下,运行时间的少量增加是可以接受的。

4.2 验证合成机制的重要作用

GA-ETS算法融合任务合成机制后得到GA-TM-ETS算法。本节将GA-TM-ETS算法和GA-ETS算法对比,验证合成机制在GA-TM-ETS算法中的重要作用,实验结果如表3及图15所示。

表3 GA-ETS算法和GA-TM-ETS算法结果Table 3 Results of GA-ETS algorithm and GA-TM-ETS algorithm

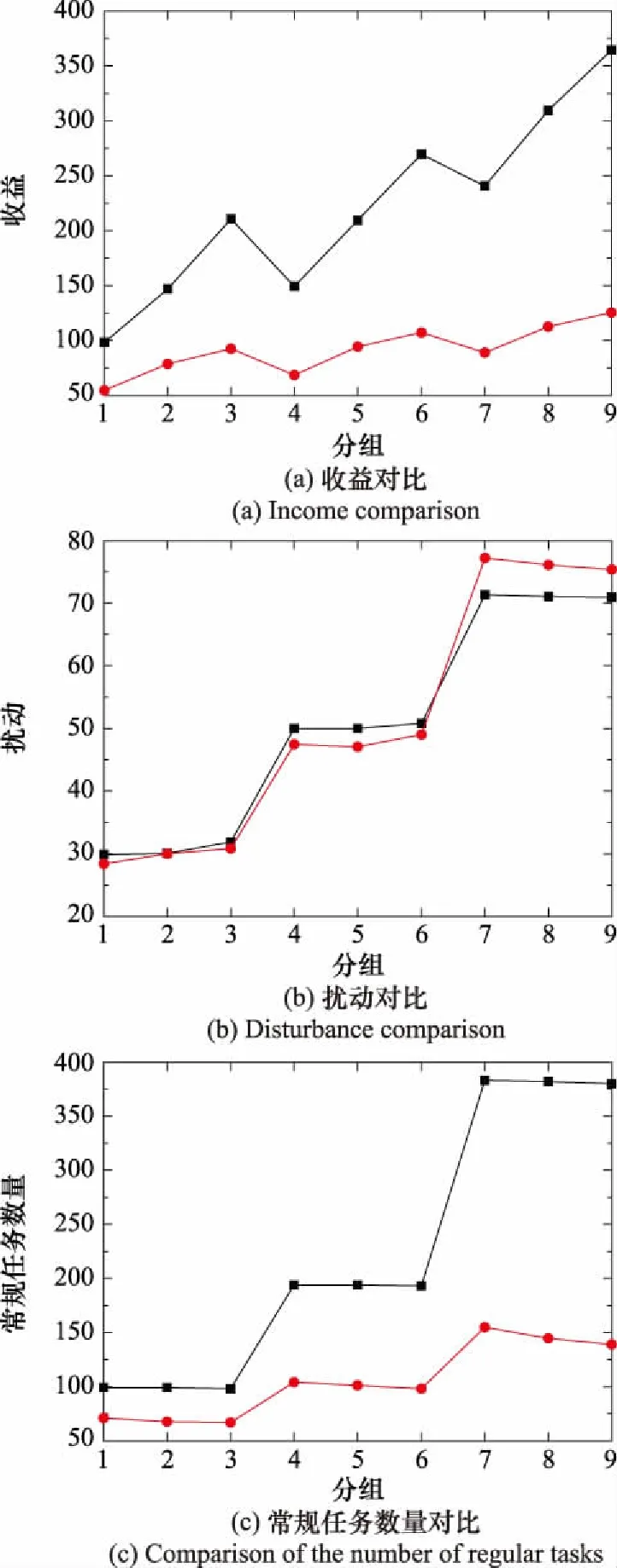
图15 GA-TM-ETS算法和GA-ETS算法实验结果对比Fig.15 Comparison of experimental results of GA-TM-ETS algorithm and GA-ETS algorithm

分析表3中两算法收益列和图15(a)可知,9组任务规模下,GA-TM-ETS算法获得的观测收益都明显高于GA-ETS算法。其次,当常规任务规模为100时,应急任务规模为20、40、60情况下,GA-TM-ETS算法观测收益分别超出GA-ETS算法43.66、68.25、118.12;当常规任务规模为200时,应急任务规模为20、40、60情况下,GA-TM-ETS算法观测收益分别超出GA-ETS算法80.72、115.1、162.34;当常规任务规模为400时,应急任务规模为20、40、60情况下,GA-TM-ETS算法观测收益分别超出GA-ETS算法151.59、196.80、238.92,即当常规任务规模不变时,随着应急任务规模增大,GA-TM-ETS算法超出GA-ETS算法的观测收益差值增大,说明任务合成机制在越大应急任务规模下效果越明显。

分析表3中两算法扰动列和图15(b)可知,当常规任务数量为100和200时,GA-TM-ETS算法的扰动量大于GA-ETS算法,但差值在区间(0,3)内;当常规任务数量为400时,GA-TM-ETS算法的扰动量小于GA-ETS算法,且差值最大为5.9。此现象出现的原因可以解释为:当任务间存在冲突时,任务合成机制的存在可以将冲突的常规任务与应急任务在原位置合成观测或在其他位置合成观测,减少对常规任务的拒绝或移位,有效减少对原序列的扰动量。但当常规任务数量为100和200时,任务合成机制对于减小扰动量的作用效果不明显,当常规任务数量为400时减小扰动量的效果较明显。

如表3中两算法常规任务和应急任务完成数量列及图15(c)和图15(d)所示,同等任务规模下,GA-TM-ETS算法的常规任务和应急任务完成数量都远大于GA-ETS算法。GA-TM-ETS算法能够表现出良好性能的原因在于,合成策略有效避免了任务时间窗之间的冲突,将原本因存在时间窗冲突或姿态转换时间不足而拒绝的任务合成观测,且合成观测具有联合收益,最终在增加了任务观测数量的基础上,大大提高了任务观测收益。

分析表3中两算法运行时间列可知,9组任务规模下,GA-TM-ETS算法的最长运行时间不超过86 s,且算法调度的任务数量和获得的观测收益明显好于GA-ETS算法,说明该算法可以在应急任务开始调度的较短时间内及时高质量完成调度。

4.3 参数敏感性分析

不同参数值的设置会直接影响算法性能。GA-TM-ETS算法以传统遗传算法为设计基础,其中涉及少量参数,如交叉概率、种群规模等。不同的参数组合会获得不同的调度结果,但各参数间存在多种参数组合,所有参数最优组合很难被找到。

启发式算法可以获得问题的较优解或以一定概率获得问题的最优解,在求解的过程中,最好状态是达到问题目标和时间成本之间的平衡状态,牺牲大量的时间获得更好的解的做法往往是不科学的。本文在9组任务规模下,采用控制变量法,在不同的参数组合下进行大量的实验,分析不同任务规模下的参数敏感性,试图找到任务观测收益和消耗时间之间的平衡状态。

图16展示3种不同应急任务规模下,5种不同交叉概率和种群规模的组合实验结果。分析图16可知,无论在何种任务规模下,程序运行时间随着种群规模的增大几乎呈现线性增长,各个交叉概率的设置值对程序运行时间不会产生明显影响。在不同的交叉概率下,随着种群规模的增大,适应度值出现峰值。经实验结果分析, GA-TM-ETS算法中参数最终设置为:应急任务规模为20时,交叉概率为0.80,种群规模为60;应急任务规模为40时,交叉概率为0.85,种群规模为80;应急任务规模为60时,交叉概率为0.80,种群规模为80。

图16 GA-TM-ETS算法不同种群规模和交叉概率的参数敏感性分析Fig.16 Parameter sensitivity analysis of GA-TM-ETS algorithm with different population sizes and crossover probability

5 结 论

本文主要研究多星应急任务调度问题。首先,根据应急任务特点,考虑应急任务完成时间和观测收益的关系,建立具有时间依赖性收益的合成任务数学规划模型。其次,以遗传算法为基础设计GA-TM-ETS算法求解问题。算法以应急任务优先调度为原则,首先设计任务合成、插入和替换算子完成应急任务向常规调度序列的插入操作。再次，考虑任务观测收益、序列扰动和最短观测时间等因素设计适应度函数,提高算法搜索速度。然后，根据编码方式,设计基于组基因的交叉算子和变异算子,结合全局修复算子完成序列寻优。最后,通过对比实验对算法的性能进行分析和比较,结果表明GA-TM-ETS算法可以在保证观测总收益且最小化对原调度序列的扰动的基础上解决多星应急任务调度问题。

在未来工作中依旧存在许多待解决的问题:① 优化数学模型,比如增加用户对成像卫星类型的要求约束和考虑成像质量的约束;② 考虑现实情况,在任务可见时间窗内考虑观测时间窗的提前或延迟策略,增强任务调度的鲁棒性。