基于LCSS的目标航线规律快速匹配方法
2022-04-07徐秋坪屈德涛刘钢墩
徐秋坪, 赵 锴, 屈德涛, 刘钢墩
(中国电子科技集团公司第二十八研究所, 江苏 南京 210007)
0 引 言
现代战争中传感器信息数量巨大,战场态势瞬息万变,指挥员需要在短时间内感知整个战场态势变化趋势并迅速做出决策,因此有必要开展对空战场态势智能化分析领域的研究。考虑战场实时目标掌握信息有限的情况,如何利用日常积累的空战场目标历史活动航线规律经验知识,分析出与之匹配的活动规律信息,为目标识别判性、运动趋势预测、威胁意图研判等战场态势智能分析提供技术手段是一个值得研究的课题。
针对战场实时目标活动航线规律匹配问题,目前国内外研究文献很少,其中一些轨迹相似度量算法可提供一定的解决思路。轨迹相似度量方法一般包括:基于点方法,如编辑距离(edit distance on real sequence, EDR)、动态时间规划(dynamic time warping, DTW)、最长公共子序列(longest common sub sequence, LCSS)等;基于形状的方法,如Fréchet、Hausdorff;基于分段的方法,如单向距离(one way distance, OWD), 多线位置距离(locality in-between polylines, LIP)。DTW和欧式距离对轨迹的个别点差异性非常敏感,如果两个时间序列在大多数时间段具有相似的形态,仅仅在很短的时间具有一定的差异(即很小的差异也会对相似度衡量产生影响),欧式距离和DTW无法准确衡量这两个时间序列的相似度,而LCSS能处理这种问题。文献[13]以实时无线传感器网络数据为例,提出基于LCSS的多元数据集相似度计算算法。文献[14-15]利用LCSS对客户运动定位轨迹进行分组,以找到热点区域并提取客户主要轨迹。文献[16]探索了一种不改变汽车总行程的轨迹自适应相似度匹配模式,并采用基于LCSS的时空相似度识别算法对所有匹配项进行筛选。此外,文献[17-18]从时空相似度维度考虑,提出了基于海量数据集的轨迹相似度匹配模型。文献[19-22]针对轨迹数据地图匹配问题和不同类型轨迹数据,利用隐马尔可夫模型或权重自适应隐马尔可夫模型等模型提出了多种地图匹配算法。活动航线规律和实时目标飞行航迹均由离散航迹点组成,活动航线规律空域跨度大、航线轮廓复杂、航迹点间距分布无规则,实时目标运动具备时效性并且掌握的航迹点一般具有周期性,时间跨度较小,离散点间距相对较小。积累的目标历史活动航线规律数据量相对较大,战场实时目标活动范围较为分散并且可能存在信息要素不完整,考虑实时目标与航线规律的特征差异性,同时需要满足对战场态势快速研判的需求,这些因素为活动规律匹配算法模型提出了更高的时效性要求。如何快速地针对单批目标从大量的规律知识库中匹配出相应的航线规律是文本研究的重点。
综合考虑本文需要解决问题的快速性、时效性、简单易于实现等需求,本文运用LCSS,结合滑窗处理、最小矩形区域过滤等处理手段,提出了一种简单、快速、精度高并且易于工程实现的航线规律匹配算法模型,解决战场实时目标运动航迹快速、准确匹配问题,可为实时目标识别判性、运动趋势预测、目标异常活动告警等方面实际工程应用提供一定的技术支撑,具有较大的工程实际应用价值。
1 问题描述
记={,,…,},>1表征积累的目标活动航线规律数据集。={,},1≤≤表征单条航线规律信息,其中,为该航线规律的基本信息,为由若干离散航迹点组成的规律航迹。记={,,,,,},其中为目标所属国家地区,为目标名称,(,,,)分别为最小经度、最小纬度、最大经度和最大纬度,构成了该目标航线规律的活动阵位。记={,,…,},表示该规律航迹的总航迹点数,其航迹点表示为={,,},1<<,其中,,分别表示该航迹点的经度、纬度和高度。根据规律航迹可求得目标航线规律的活动阵位信息(,,,)。
实时目标信息可描述为={,},其中为实时目标的基本信息,为一段时间内该目标运动航迹。记={,},其中为实时目标所属国家地区,为实时目标名称。记={,,…,},表征当前掌握的该实时目标运动航迹点总数,其单个航迹点信息可表示为={,,},1<<,其中,,分别表示该航迹点的经度、纬度和高度。
航线规律主要表征了目标历史频繁行动的轨迹轮廓特性,其规律航迹点主要表现为空间特征,且航迹点分布较为稀疏。另外,不同目标的航线规律活动阵位分布较散,空间跨度相差较大。实时目标记录的航迹点信息一般具有周期性,时间跨度较小,与航线规律的航迹点密度相差较大。此外,在工程实践应用中,实时目标基本信息感知度较低,存在掌握的基本信息要素不全问题,基于国家地区、目标名称信息直接检索相应航线规律存在局限性。另外,战场态势瞬息万变,为满足目标快速识别研判需求,对实时目标航线匹配的时效性提出了更高要求,复杂的匹配算法模型显然是不可取的。考虑上述问题和需求,基于掌握的实时目标信息,本文提出了一种简单、快速、高效并且易于工程实现的航线规律匹配算法。
2 航线规律匹配模型
针对上述问题,在积累的目标航线规律数据基础上,采用滑动窗口处理、活动阵位特征过滤、数据格式化处理等手段,基于LCSS求解两航迹最长公共子序列方式,提出了一种快速实用的航线规律匹配算法,具有较高的匹配效率和准确度。本文提出的航线规律匹配算法模型逻辑处理流程如图1所示。

图1 航线规律匹配模型逻辑处理流程Fig.1 Logic processing flow of trajectory rule matching model
首先对实时目标采用动态滑动窗口机制进行处理,提取满足一定时间约束的航迹信息并分析其活动阵位,以保证目标运动特征的时效性;其次,基于实时目标基本信息、活动阵位特征等信息,对积累的航线规律数据集进行过滤,提取与实时目标有关联度的航线规律,以减少用于匹配的规律数据量;进一步,采用区域滑窗机制对相关联的航线规律提取有效航迹段信息,以减小匹配模型计算量,降低内存消耗;然后,基于实时目标运动航迹特征对相关航线规律的有效航迹进行数据格式化处理,避免航线规律数据因跨度大导致的航迹点稀疏问题;最后,基于格式化处理的有效航线规律和实时目标运动航迹数据,求解最长公共子航迹序列,计算航线规律匹配度。
匹配模型具体设计过程描述如下。
(1) 采用动态滑窗处理模式提取实时目标有效航迹段,并计算目标当前活动阵位。
该滑窗是根据实时目标航迹点数量来设计窗口大小,该窗口大小是动态变化的。假设实时目标最大航迹点数量为,那么窗口最大长度可视为个航迹点组成的长度。
记表征该滑窗大小,如果记录的实时目标航迹点数目小于,那么为当前数量航迹点组成的长度;如果记录的实时目标航迹点数目不小于,那么为个航迹点组成的长度。滑窗大小可描述为
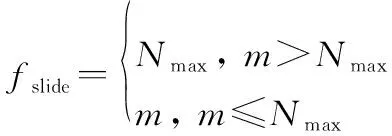
(1)
基于航迹点数量的滑窗提取实时目标有效航迹点时,均从最新记录时刻的航迹点开始,以保证用于航线规律匹配分析数据的时效性,如图2所示。进而,用于匹配分析的实时目标航迹可描述为={,,…,},可以看出,应满足≤。进一步,可根据航迹点特征信息,计算该目标当前活动阵位{,,,},其中,,,分别为最小经、纬度和最大经、纬度。
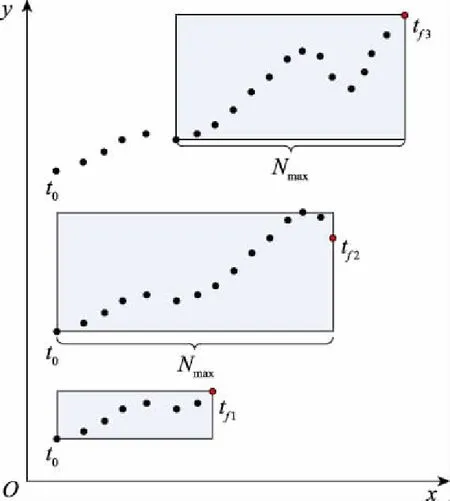
图2 实时目标有效航迹提取的滑窗设计Fig.2 Design of sliding window for real time target effective trajectory extraction
(2) 基于实时目标基本信息、活动阵位特征过滤获取相关联的航线规律数据。
考虑到掌握的航线规律数据量较大,直接将目标实时有效航迹与规律航迹进行匹配,则计算量太大,耗时较高。因此,可通过实时目标基本信息、有效航迹的活动阵位特征进行过滤处理,得到与之相关联的规律航线数据。
假设活动阵位关联阈值为,基于实时目标活动阵位特征{,,,},可构建最小矩形区域。根据该矩形区域和航线规律活动阵位信息,判断二者的相关性,提取与实时目标相关联的航线规律,如图3所示。通过遍历所有航线规律,根据各规律活动阵位{,,,}组成的矩形区域与是否存在交集来判断该条规律是否与目标具备初步相关性。如果相关,则记录该条规律,否则跳过处理下一条规律,如图3中航线规律和与目标具备初步相关性,则不相关。

图3 基于活动阵位的航线规律过滤示意图Fig.3 Schematic diagram of trajectory rule filtering based on active positions
如果能够获悉实时目标的所属国家地区、机型等基本信息,则可利用基本信息进行预先检索,进一步加快航线规律过滤效率,缩短过滤时间。
(3) 提取与实时目标相关联的航线规律有效航迹段。
针对航线规律存在空域跨度大的特点,对于存在阵位相关的航线规律而言,虽然与实时目标活动阵位有一定交集,但是该规律可能与目标当前阵位相关联的有效航迹段只占据整个航线规律中的较少部分。如果直接将航线规律与目标实时航迹进行匹配,不仅增加了不必要的计算量和计算时间,也增加了内存消耗,不利于快速分析计算。因此,有必要对具有相关性的航线规律进一步处理,提取其有效航迹段信息。

图4 提取航线规律的有效航迹Fig.4 Effective track extraction of trajectory rule
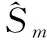

(2)
有效航迹段对应的航迹点数可表示为
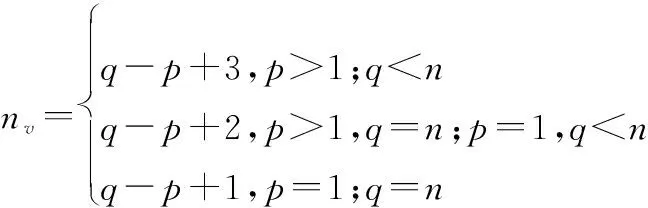
(3)
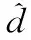
经过上述处理可得到与实时目标相关联的航线规律及其有效航迹数据,为便于描述,记为={,,…,},≤,单条航线规律可描述为={,},1≤≤。
(4) 航线规律有效航迹段数据格式化处理。
为避免航线规律有效航迹段的稀疏、空间跨度大以及有效航迹点数量较少带来的匹配误差,可对规律航迹数据进行格式化处理。
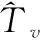

图5 有效航迹段数据格式化处理示意图Fig.5 Schematic diagram of effective track segment data format processing
(5) 基于格式化处理的有效航线规律和实时目标运动航迹,求解最长公共子航迹序列,计算匹配度。

最长公共子航迹序列计算方法可描述为

(4)


在计算最长公共子航迹序列过程中,对于Dis(,)<条件下的航迹点对,可计算其点对之间的距离计算其距离匹配程度,本文采用距离的线性关系计算点对距离匹配度:

(5)
式中:为点对距离匹配因子,且0<<1。本文取=025,则的取值范围为075~1。
考虑公共航迹子序列匹配情况,航迹点距匹配度可表示为

(6)
公共子序列航迹点数匹配度可表示为
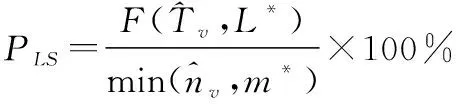
(7)
基于公共子序列的航迹点距匹配度以及航迹点数匹配度,进一步可计算两航迹综合匹配度:
=+
(8)
式中:,分别表示航迹点距匹配度因子和航迹点数匹配度因子,且满足+=1,>0,>0。本文在仿真中取=02,=08。
3 仿真分析

3.1 实时目标航迹匹配效果
模拟产生一批空中目标,在其飞行过程中对其不同时段进行采样匹配分析,用记录的航迹点数来表征其在不同时段航迹掌握情况,基于本文提出的航线规律匹配模型,其在不同阶段的匹配分析结果如图6所示,相应匹配结果参数如表1所示。图6中蓝、粉红、黑、绿、黄色标注的各离散点表征实时目标在不同阶段用于匹配分析的航迹点信息,亮蓝线和红点表征的是与实时目标各阶段运动航迹相匹配的航线规律信息,其中红色点为航线规律的各航迹点。仿真结果表明,基于本文提出的规律匹配模型,基于实时目标运动航迹可以有效匹配出与之关联的航线规律,并提供相应的匹配度指数。在匹配分析时如果实时目标记录的航迹点数目超过设定值,则用于匹配计算的目标航迹为截止当前最新的个航迹点,其早期记录的若干航迹点不作为匹配计算范畴,如图6(d)和图6(e)所示,不仅充分利用了对当前目标分析的时效性,而且大大减少了计算所耗时长,提高匹配效率。此模型计算时长随着航迹点数的增加而增大,当达到后,计算时间相对稳定,从千余条航迹规律中匹配分析计算时间约在1 s左右。


图6 不同阶段下规律匹配结果Fig.6 Rule matching results in different periods
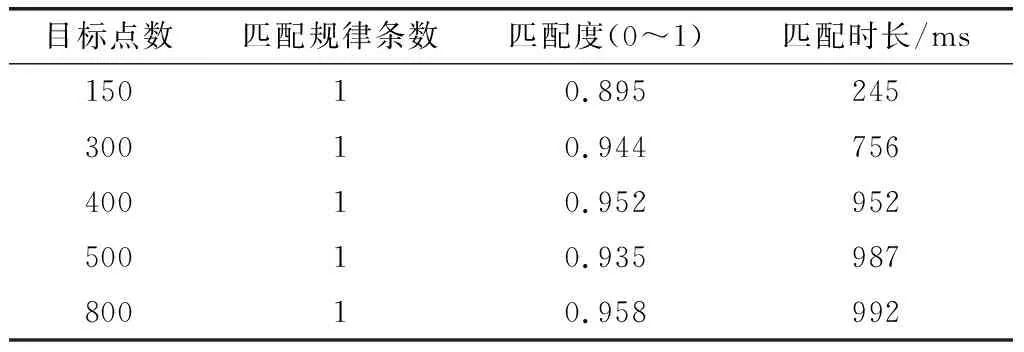
表1 不同阶段匹配参数
3.2 不同航迹窗口下对比分析
不同决定了用于匹配分析时实时目标航迹过滤窗口以及用于匹配计算的航迹点数量,通过设置不同的分析其对匹配效果的影响。仿真数据采用上述模拟目标在800点时的运动状态,设置不同仿真结果如图7所示,相应匹配参数如表2所示。仿真结果表明,值越大,则计算时间会相对较长,但对实时目标分析的实效性和快速性相对较低。不同的对摄取的航线规律航迹点数量不同,考虑规律航迹点稀疏程度不确定性,如果确定的窗口范围内航线规律航迹点数较为稀疏且航迹点间距跨域较大,则会增加有效航迹段数据格式化处理时间。值越小,虽然可以减少计算时间,但是存在不能充分表征目标运动特性的风险,造成匹配规律存在虚警现象。采用本文提出的模型能够综合考虑战场态势分析的时效性和匹配分析的快速性,有效避免采用所有航迹点进行匹配分析所带来的长耗时问题。在实际工程使用中,值可根据具体需求综合考虑分析的时效性以及快速性进行调优。
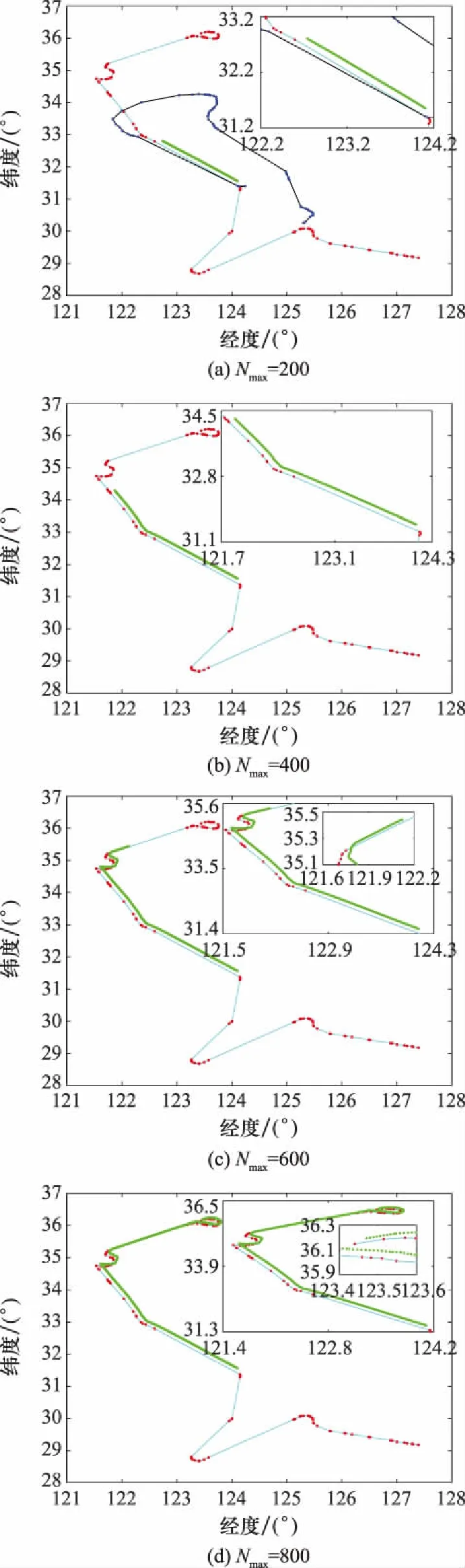
图7 不同Nmax的匹配结果Fig.7 Matching results with different Nmax

表2 不同Nmax的匹配参数
4 结 论
本文提出的算法模型能够快速、有效地实现实时目标运动航迹与活动航线规律知识的准确匹配。该方法简单可行,易于工程实现,并且能够综合考虑战场态势分析的时效性和快速性,可为实时目标识别判性、运动趋势预测、目标异常活动告警等方面的态势智能化分析提供一定的技术支撑,具有较大的工程实际应用价值。
