基于改进IFRS相似度和信息熵的反导作战目标威胁评估

卢盈齐, 范成礼, 付 强, 朱晓雯, 李 威

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

反导作战目标威胁评估是智能辅助决策的关键技术,如何快速精确评估来袭弹道导弹的威胁程度是反导指挥决策亟待解决的技术难题。

当前,目标威胁评估方法常用的有贝叶斯网络、D-S证据理论、模糊推理、多属性决策等。文献[1]针对防空目标威胁评估中存在样本数据量较少的问题,提出了基于约束参数学习的动态贝叶斯网络威胁评估方法;文献[2]考虑了探测数据不确定性,提出了基于模糊动态贝叶斯网络的空中目标威胁评估方法。然而,贝叶斯网络虽能有效处理不确定信息,但转移概率的选取依赖于专家经验,可靠性较差,且仅适用于存在大量样本数据的情况,对于小样本数据的求解精度较差,不适用于缺少作战样本数据的反导作战。文献[3]研究了基于证据理论的助推段弹道导弹目标威胁评估方法。然而D-S证据理论对于冲突信息处理能力较弱,问题空间较大时会出现组合爆炸问题。

受限于来袭目标复合干扰和传感器探测能力的限制,反导作战中存在大量不确定因素,基于不确定理论研究弹道导弹目标威胁评估已成为国内外研究热点。由于弹道导弹威胁巨大,目标的特征属性众多,一旦漏截将面对防御资产极大的破坏,对目标威胁评估精度要求较高,因此不确定环境下的反导作战目标威胁评估需考虑多种因素,其实质是一类不确定多属性决策问题。在众多不确定理论中,Atanassov提出的直觉模糊集理论去除了隶属度与非隶属度和为1的约束条件,可以更加细致地刻画不确定性。Pawlak提出的粗糙集理论亦是处理不确定性信息的有效数学工具,它的优势在于无需数据集以外的先验信息,已成功地应用于决策分析、模式识别、机器学习等领域。然而由于粗糙集理论处理不确定原始数据的机制不完善,与其他不确定理论有很强的互补性。

鉴于此,本文将粗糙集理论和直觉模糊集理论有效结合,一方面通过细分直觉模糊粗糙集(intuitionistic fuzzy rough set,IFRS)犹豫度,提出改进的IFRS相似度模型;另一方面针对IFRS下近似隶属度、上近似隶属度、下近似非隶属度、上近似非隶属度偏差相等时,现有IFRS信息熵存在与直觉事实不相符的问题,提出基于余弦函数的IFRS信息熵,确定目标属性权重。然后,在构建反导目标威胁评估指标体系和量化目标属性的基础上,结合基于理想解相似程度的排序方法(technique for order preference by similarity to ideal solution,TOPSIS),提出基于改进IFRS相似度和信息熵的反导作战目标威胁评估方法,实现目标威胁排序。最后通过仿真实例验证该方法的可行性和有效性。

1 基本理论

设为模糊粗糙集之集合,∀∈中的上近似和下近似分别为、,则中的一个IFRS为

={〈,(),(),(),()〉|∀∈}

式中:():→[0,1],():→[0,1]分别代表的下近似隶属函数和上近似隶属函数;():→[0,1],():→[0,1]分别代表的下近似非隶属函数和上近似非隶属函数,满足以下条件:

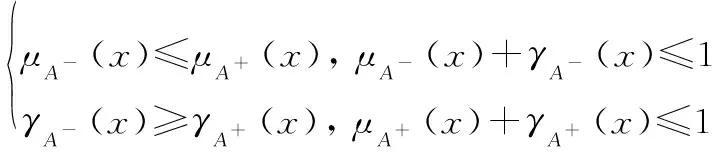
犹豫度()可表示为

()=1-()-()

式中：()可描述IFRS自身存在的犹豫程度,()越大表明不确定性越大。显然,对于每一个∈,0≤()≤1。

设,是论域={,,…,}上的IFRS,设=〈(),(),(),()〉,=〈(),(),(),()〉分别是在,中的直觉模糊粗糙值,则IFRS相似度可定义为

(1)

根据定义2,IFRS相似度函数(,)满足下列性质:

(1) 0≤(,)≤1;

(2)(,)=(,);

(3)(,)=1,当且仅当=;

(4)(,)=0,当且仅当

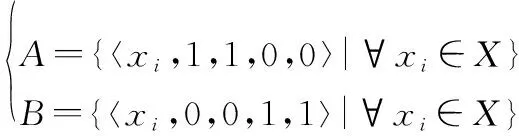
或者

2 改进的IFRS相似度模型

(,)可描述两个直觉模糊粗糙值之间的相似程度。从定义2可以看出,(,)仅考虑了不同直觉模糊粗糙值之间的差异,忽略了其自身存在的犹豫度(),无法描述“非此非彼”的中立状态。当两个直觉模糊粗糙集的下近似隶属度()、上近似隶属度()、下近似非隶属度()、上近似非隶属度()的偏差均相等时,会出现计算结果与直觉事实不符,评估精度不高的问题,如下所示。

投票系统中,()表示赞成票数比,()表示可能赞成票数比(赞成和弃权之和);()表示反对票数比,()表示可能反对票数比(反对和弃权之和);犹豫度()描述中立的弃权票数比。设,,是论域={,}上3个的直觉模糊粗糙集:

={〈04,07,04,01〉, 〈,05,08,05,02〉}

={〈03,06,05,02〉, 〈,04,07,04,01〉}

={〈03,08,05,00〉, 〈,04,09,06,01〉}

在投票模型中,赞成票数比对应隶属度函数值,反对票数比对应非隶属度函数值,由此可得=03,=03,=05。根据,,直觉模糊粗糙集数据可得投票系统票数如表1所示。

表1 投票系统Table 1 Voting system

由表1可以看出,对于赞成票和反对票,,和,均相差1票;但对于弃权票,,一样,,却相差2票。因此可认为,的相似度要高于,的相似度。然而,由式(1)可得

{(,)=090

(,)=090

其中,(,)=(,),显然与直觉不符。为克服该问题,并有效提高直觉模糊粗糙集相似度计算精度,本文充分考虑集合自身存在的不确定性,对犹豫度进行细分,上近似隶属度对应上近似犹豫度,下近似隶属度对应下近似犹豫度,并基于欧式距离提出改进的IFRS相似度模型。

设,是论域={,,…,}上的IFRS,设=〈(),(),(),()〉,=〈(),(),(),()〉分别是在,中的直觉模糊粗糙值,则改进的IFRS相似度可定义为

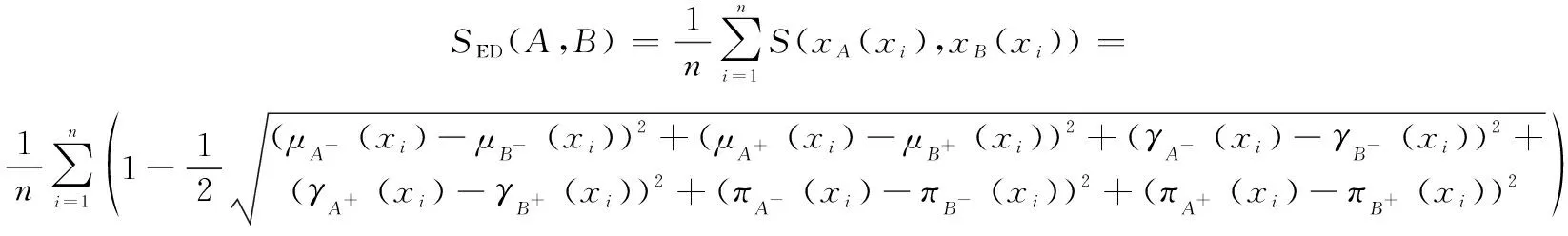
(2)

式中：()表示的下近似犹豫度,()=1-()-();()表示的上近似犹豫度,()=1-()-()。

式(2)定义的(,)是一个直觉粗糙集相似度,满足性质1中4个条件。

(1) 针对条件1,由于

()=1-()-()

()=1-()-()

可得

(()-())= (()-())+(()-())+ 2(()-())(()-())

同理:

(()-π())= (()-())+(()-())+ 2(()-())(()-())

代入式(2)可得

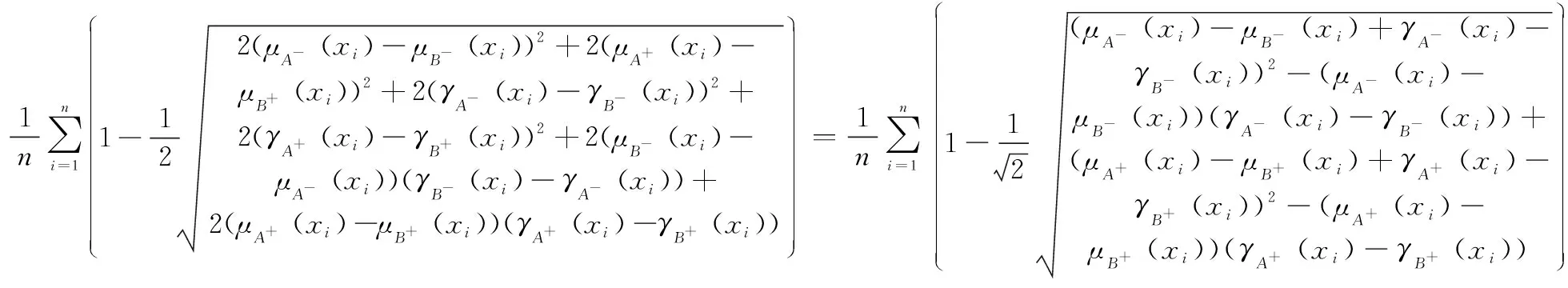
由于

()+()≤1,()+()≤1

可得

(()-()+()-())≤1

由于

(()-())(()-())≤1

可得

0≤(()-()+()-())- (()-())(()-())≤1

同理:

0≤(()-()+()-())- (()-())(()-())≤1

可得

0≤(()-()+()-())- (()-())(()-())+ (()-()+()-())- (()-())(()-())≤2

因此,0≤(,)≤1。

(2) 条件2显然成立。

(3) 针对条件3,若(,)=1,则

(()-())+(()-())+ (()-())+(()-())+ (π()-π())+(π()-π())=0

于是

()=(),()=()()=(),()=() π()=π(),π()=π()

因此,=。

(4) 针对条件4,(,)=0,则

(()-())+(()-())+ (()-())+(()-())+ (π()-π())+(π()-π())=4

于是

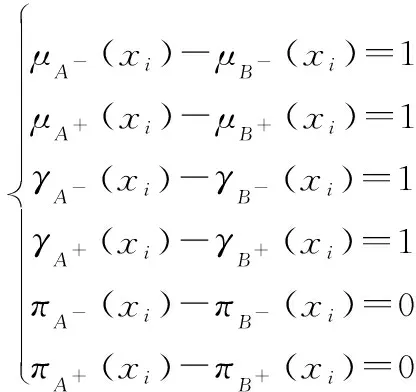
因此,

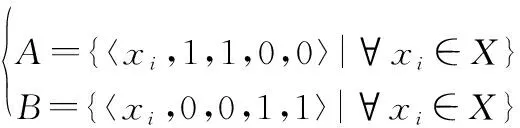
或者,

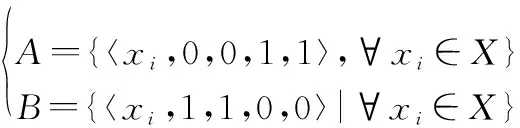
证毕

根据式(2)计算例1中,的相似度和,的相似度为

{(,)=0863 4

(,)=0829 3

其中,(,)>(,),显然该结果更符合直觉事实,以该模型为基础可以更精确地刻画IFRS之间的相似程度,提高不确定环境下目标威胁评估的精度。

3 基于余弦函数的IFRS信息熵

目标属性确定是反导目标威胁评估的关键。熵值法是典型的权重确定方法,可表示目标属性的相对重要程度。统计学表明,信息熵越小,提供的信息量越多,对应目标的权值应越大。现有关于直觉模糊粗糙集信息熵的测量方法,下近似隶属度、上近似隶属度、下近似非隶属度、上近似非隶属度偏差相等时,存在与直觉事实不相符的情况。为克服该问题,本文提出基于余弦函数的直觉模糊粗糙集信息熵。

设是论域={,,…,}上的IFRS,则基于余弦函数的IFRS信息熵()可定义为

()=

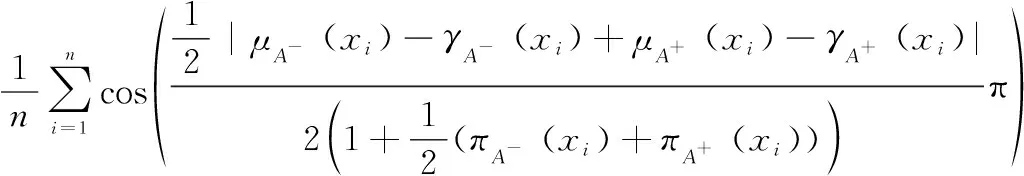
基于余弦函数的直觉模糊粗糙集信息熵()具有如下性质:

(1)()=0,当且仅当为经典集;

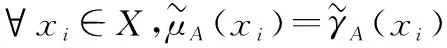
(1) 若为经典集,则()=()=1,()=()=0且π()=π()=0;或()=()=0,()=()=1且π()=π()=0。因此,()=0。

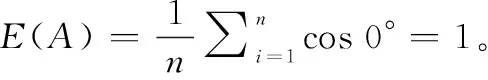
证毕

基于余弦函数的直觉模糊粗糙集信息熵不但考虑了下近似隶属度、上近似隶属度、下近似非隶属度、上近似非隶属度的偏差而且考虑了上近似犹豫度和下近似犹豫度对熵值的影响,因而能够更加有效地刻画直觉模糊粗糙集的不确定程度,为目标属性权重未知情况下的反导作战目标威胁评估奠定基础。

4 基于改进IFRS相似度和信息熵的反导作战目标威胁评估方法

4.1 IFRS条件下的反导目标威胁评估问题描述

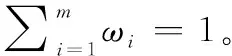
=(〈1(),1(),1(),1()〉, 〈2(),2(),2(),2()〉,…, 〈 (), (), (), ()〉)

式中：()∈[0,1],()∈[0,1],()∈[0,1],()∈[0,1]分别表示目标∈满足、可能满足、可能不满足、不满足属性∈的程度。()+()≤1,()+()≤1,()≤(),()≥()。

4.2 反导作战目标威胁评估指标体系构建

弹道导弹的目标特征可以采用多种指标进行描述。本文根据反导防御系统传感器对来袭目标的探测信息,从目标的空域分布、红外特性和电磁特性3个方面入手,考虑目标位置、速度、辐射温度、极化特性、雷达截面积(radar cross section, RCS)等5个属性作为二级指标威胁因子,以此构建反导作战目标威胁评估指标体系,如图1所示。表2给出了各评估指标的类型。

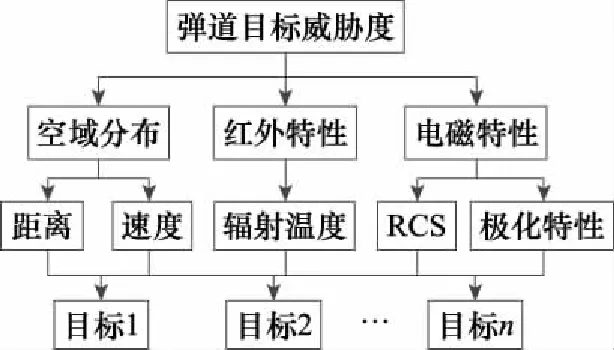
图1 目标威胁评估指标体系Fig.1 Indicator system of target threat assessment

表2 评估指标属性和类型

4.3 目标属性威胁度量化

模糊隶属度函数和非隶属度函数是量化目标属性的有效方法。本文根据弹道导弹目标群的属性特点,采用半S形分布、半Z形分布及G. A. Miller 9级量化理论对各来袭目标(弹头、重诱饵、轻诱饵及碎片)属性进行量化。

(1) 距离、速度属性

弹道导弹真弹头的质量大于轻、重诱饵及碎片的质量,在未加速机动的条件下,真弹头的位置和速度变化量相对较小。因此,可认为目标的距离、速度变化量越小其威胁度越大,服从半S形分布,如图2所示。其隶属度和非隶属度求解方法分别如下所示:

(3)

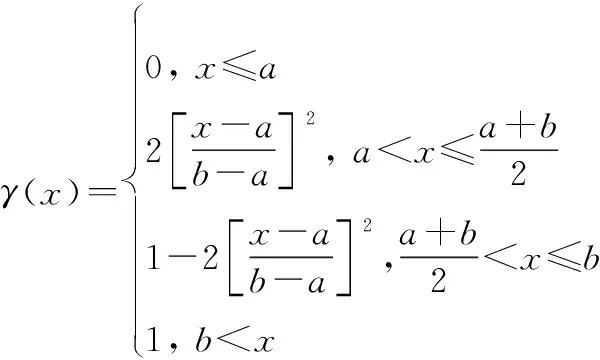
(4)

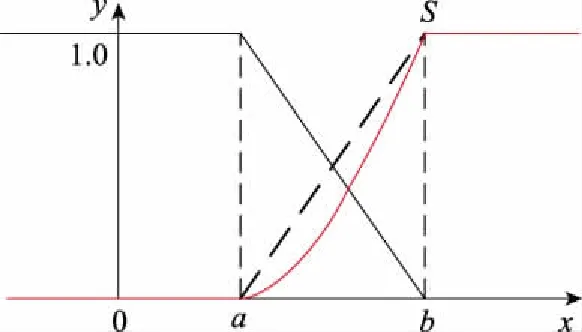
图2 半S形分布图Fig.2 Half S distribution diagram

(2) 辐射温度、RCS属性

轻、重诱饵及碎片的辐射温度和RCS均小于真弹头,可认为目标辐射温度、RCS变化量越大其威胁度越大,服从半Z形分布,如图3所示。其隶属度和非隶属度求解方法分别如下所示:

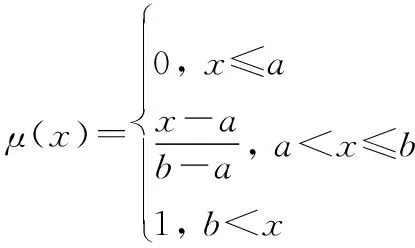
(5)

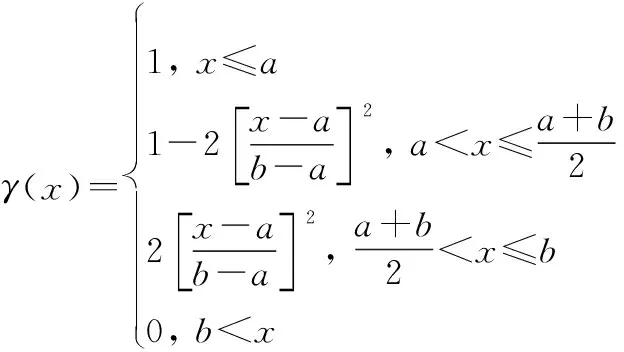
(6)

图3 半Z形分布图Fig.3 Half Z distribution diagram

(3) 极化特性属性

极化特性属性变化没有特定规律,可采用G. A. Miller 9级量化理论进行量化,量化结果与直觉模糊粗糙数对应关系如表3所示。

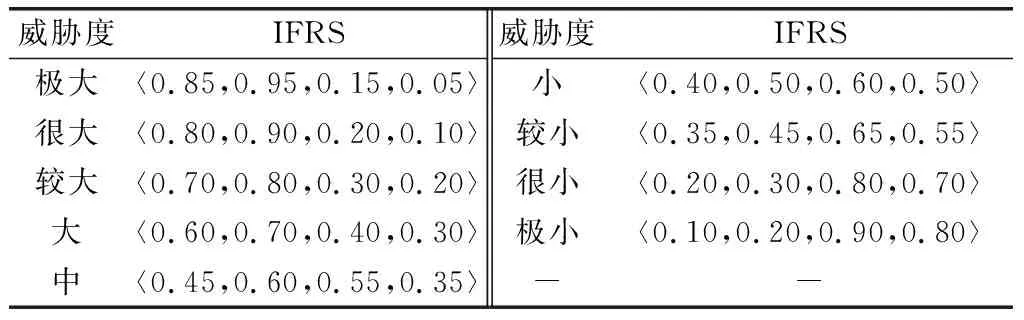
表3 9级量化结果与IFRS对应关系Table 3 The corresponding relationship between 9-level quantization results and IFRS

4.4 基于TOPSIS的直觉模糊粗糙数排序

IFRS条件的反导目标威胁评估问题需解决直觉模糊粗糙数排序问题。本文基于改进的IFRS相似度模型,结合TOPSIS原理,进行直觉模糊粗糙数排序。在加权决策矩阵中,正理想解为所有目标中各属性威胁度最大的解,负理想解为威胁度最小的解。对于效益型指标类型(如目标速度、辐射温度、极化特性),正理想解取指标最大值,负理想解取指标最小值;对于成本型指标类型(如目标距离、目标RCS),正理想解取指标最小值,负理想解取指标最大值,公式如下。

正理想解为

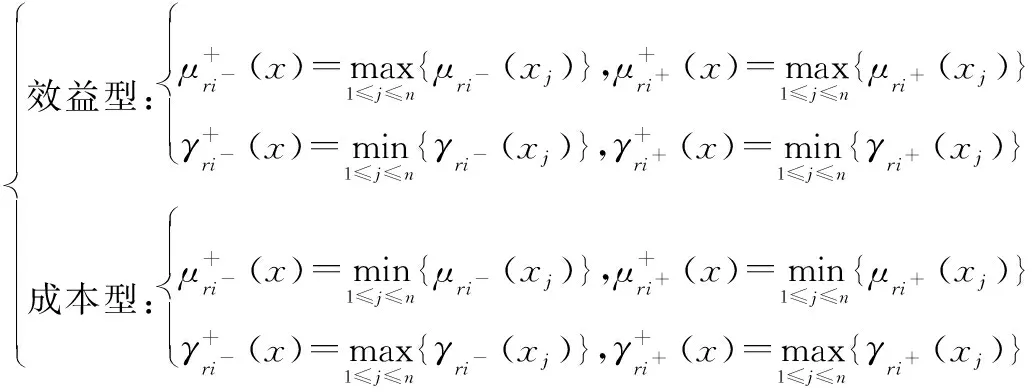
(7)

负理想解为

(8)

进一步根据式(2),计算目标与加权决策矩阵正理想解和负理想解的相似度为

(9)

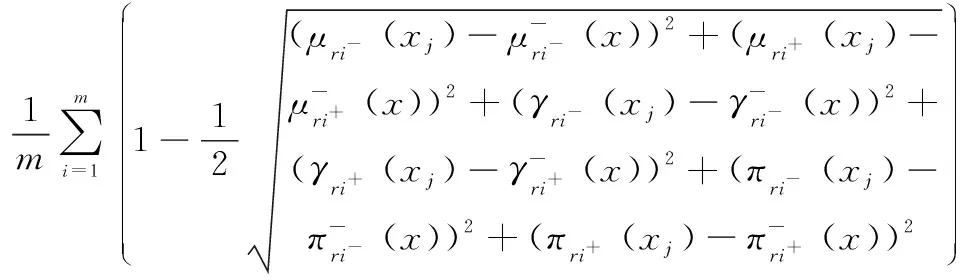
(10)

式中：

4.5 算法流程

为得到目标={,,…,}的威胁评估排序,本文在构建与量化反导目标威胁评估指标体系的基础上,利用基于余弦函数的IFRS信息熵确定目标属性权重。进一步,依据改进的IFRS相似度模型,结合TOPSIS法,提出基于改进IFRS相似度和信息熵的反导作战目标威胁评估方法,具体步骤如下。

针对威胁评估指标体系,利用式(3)～式(6)得到威胁评估决策矩阵为

=()=(〈(),(),(),()〉)×

根据式(11)计算目标各属性基于余弦函数的直觉模糊粗糙集信息熵：

(11)

建立基于最小化直觉模糊粗糙集信息熵的非线性规划模型,如下所示：

(12)

式中:是目标属性权重值。

目标属性权重={|=1,2,…,}的求解;对式(12)建立Lagrange函数：

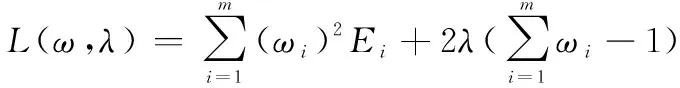
分别对和求导,并等于0,得

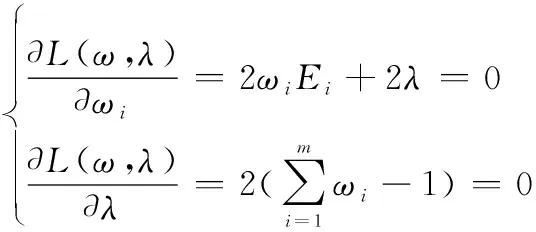
(13)

求解式(13)得到目标属性权重为

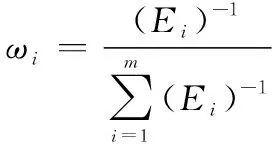
(14)

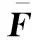
(15)

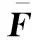
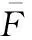
根据式(16)计算目标的威胁度值,并对所有目标威胁度进行排序。

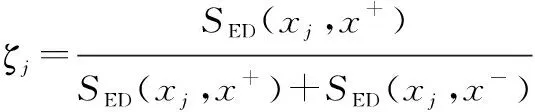
(16)

图4为基于改进IFRS相似度和信息熵的反导作战目标威胁评估算法流程。

图4 算法流程图Fig.4 Algorithm flow diagram

5 实例分析

假定某次反导演习中,反导防御系统传感器共观测到4个来袭目标,即备选方案为={,,,},现根据={距离,速度,辐射温度,RCS,极化特性}5项属性对来袭目标进行威胁评估。

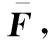
表4 决策矩阵Table 4 Decision matrix

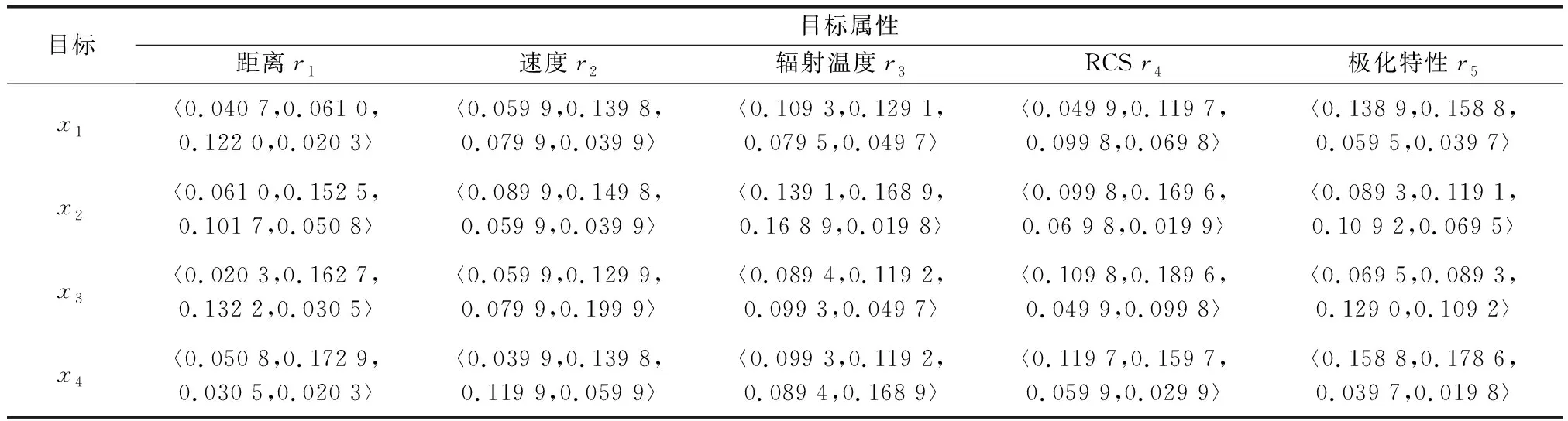
表5 加权决策矩阵Table 5 Weighted decision matrix

={〈0020 3, 0061 0, 0132 2, 0050 8〉,

〈0089 9,0149 8, 0059 9, 0039 9〉,

〈0139 1, 0168 9,0079 5,0019 8〉,

〈0049 9, 0119 7, 0099 8, 0099 8〉,

〈0158 8, 0178 6, 0039 7, 0019 8〉}

={〈0061 0, 0172 9, 0030 5, 0020 3〉,

〈0039 9, 0129 9, 0119 9, 0199 9〉,

〈0089 4, 0119 2, 0168 9, 0168 9〉,

〈0119 7, 0189 6, 0049 9, 0019 9〉,

〈0069 5, 0089 3, 0129 0, 0109 2〉}

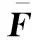
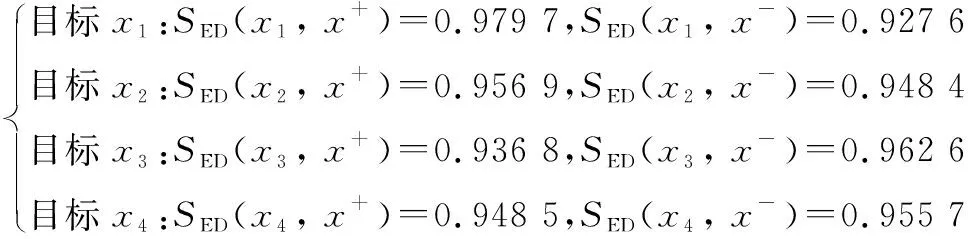
根据式(16)计算得目标的威胁度值为

=0513 6,=0502 2,=0493 2,=0498 1

可以看出目标威胁评估排序结果为

>>>

在战场态势瞬息万变的反导作战中,目标威胁评估方法的精准性主要取决于不同目标威胁度在同一评价方法中的差异性,差异性越明显,越有利于最优方案的选取,即方法优越性越强,因此目标较目标的优越度(superior degree, SD)可定义为

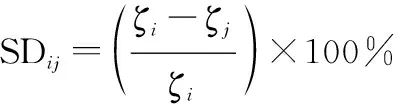
式中:和(=1,2,…,;=1,2,…,;≠)为不同目标的威胁度。

为验证本文所提方法的有效性,将本文方法与文献[16-20]所提出的方法进行对比,不同方法的目标威胁度排序结果及优越度如图5和表6所示。可以看出,本文求得的目标威胁排序结果与文献[16-19]相同,说明本文所提方法的有效性。与文献[20]排序结果略有不同,但确定的威胁度最大和最小的目标是一致的。注意到,本文所提方法中,各目标之间的优越度差距最大。在目标1和目标2的优越度对比中,本文算法的优越度分别是文献[16-19]所提方法的249、114、202、128倍;在目标2和目标4的优越度对比中本文算法的优越度分别是文献[16-19]所提方法的178、137、122、186倍;在目标4和目标3的优越度对比中,本文算法的优越度分别是文献[16-19]所提方法的185、126、204、338倍。优越度差距越大,越易于指挥员决策,充分说明了本文算法基于改进IFRS相似度和信息熵,确定目标权重和威胁度,有效提高了不确定环境下反导目标威胁评估的精度。

图5 不同方法优越度对比Fig.5 Comparative SD of different methods

表6 不同方法的目标威胁排序及优越度Table 6 Target threat ranking and SD of different methods

6 结束语

本文针对现有目标威胁评估方法的局限性,将粗糙集理论和直觉模糊集理论有效结合,改进IFRS相似度模型和基于余弦函数的IFRS信息熵,并结合TOPSIS法,提出基于改进IFRS相似度和信息熵的反导作战目标威胁评估方法。该方法克服了现有威胁评估方法由于忽略目标属性犹豫度和权重而造成评估精度不高的问题,能更好地模拟不确定作战环境,为高效指挥决策实施奠定基础。如何将本文方法推广至区间模糊数并用来解决包含区间模糊信息的多属性决策问题是下一步研究的重点。