基于吕氏分布的机动目标参数化平动补偿方法

刘丰恺, 黄大荣,*, 郭新荣, 冯存前

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 武警工程大学基础部, 陕西 西安 710086)

0 引 言

克服由目标非合作特性给ISAR成像带来的影响是提升逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像效果的重要途径。一般而言,目标的运动可以被分解为平行于雷达视线方向的运动和垂直于雷达视线方向的运动,即平动和转动。而平动补偿的目的是消去目标平动对回波的影响,保证ISAR成像的质量。对机动目标进行成像一直是ISAR成像的重点研究方向,目前诸多学者提出了多种具有良好性能的机动目标成像方法,但这些方法主要着眼于解决目标非均匀转动对ISAR成像的影响,对机动目标平动补偿的问题并未深入讨论。

传统的平动补偿方法通常分两步进行,即首先将脉冲压缩后的回波包络对齐,然后矫正由平动带来的相位误差。其中,包络对齐对精度要求相对较低且易于实现,一般采用平均距离像相关法就能稳定实现包络对齐。而相位矫正需要较高的精度,是平动补偿的重点和难点。常用的相位矫正方法包括多普勒中心法、特显点法等。这些方法在目标平稳运动时能够获得较好的效果,但当目标机动时,复杂的相位变化会使这些方法难以得到较好的结果。为了提高相位矫正的性能,部分学者提出了一系列基于相位梯度自聚焦(phase gradient autofocus, PGA)的相位矫正方法。PGA能够有效克服传统相位矫正方法的不足,但由于PGA需要进行重复的迭代运算,因此需要较大的运算量。事实上,平动对包络和相位的影响本质上是一致的,因此有学者提出对目标平动进行建模并基于图像质量估计运动参数,以实现包络和相位的同时补偿,具有一定的借鉴意义。但基于图像质量估计运动参数在信噪比较低时可能会出现较大的误差,因此亟待改进。

为了克服现有平动补偿方法的不足,实现对机动目标回波信号的准确平动补偿,本文提出一种基于吕氏分布(Lv’ s distribution, LVD)的参数化平动补偿方法。该方法将含有平动误差的机动目标回波建模为多项式相位信号,利用相位差分聚焦各距离单元的能量,然后采用LVD估计信号参数,最后利用估计得到的参数构建补偿函数,消除平动误差。实测数据实验证明了所提方法的有效性和低信噪比条件下的优越性能。

1 信号模型

现代雷达广泛采用线性调频信号作为发射信号,可以被表示为

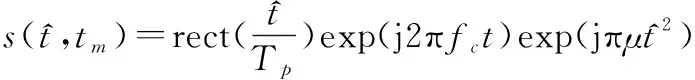
(1)

含有平动影响的ISAR成像模型如图1所示。

图1 含有平动影响的ISAR成像模型Fig.1 ISAR imaging model with translational effects

其中,()为目标平动距离;()为目标转动的总角度。

根据点散射模型,目标可以被认为由多个散射点组成,设发射信号经目标中某一散射点反射形成回波,则目标回波可以表示为

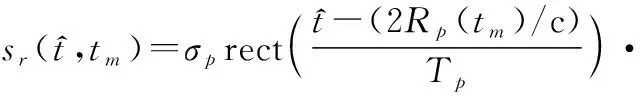
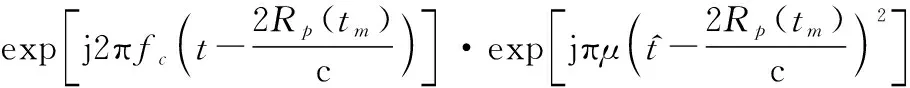
(2)

式中:()为雷达到散射点的距离,根据停跳假设,()仅与有关;c为光速。

宽带线性调频信号的脉冲压缩通常采用解线频调算法(Dechirp),对式(2)进行Dechirp处理后得到的结果为

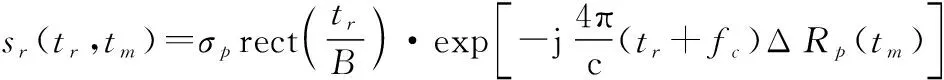
(3)

式中:为信号带宽;为等效慢时间,其表达式为

(4)

式中:为参考距离。

式(3)中的Δ()包括平动和转动两部分,其可以被写为

Δ()=()+cos(())+sin(())

(5)

式中:为散射点相对于目标中心的径向距离;为散射点相对于目标中心的横向距离。根据文献[1]和文献[28],()和()可以表示为

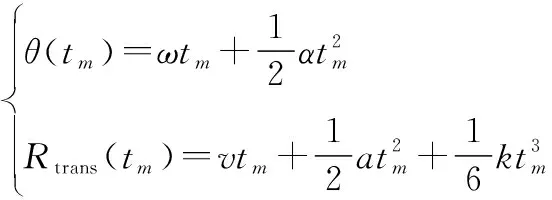
(6)

式中:为转动速度;转动加速度;为平动速度;为平动加速度;为二阶平动加速度。考虑到在ISAR成像过程中,目标转动的总角度通常较小,采用泰勒级数展开对()做近似,此时Δ()可以写为

(7)

综上,含有个散射点的机动目标回波具有如下形式:

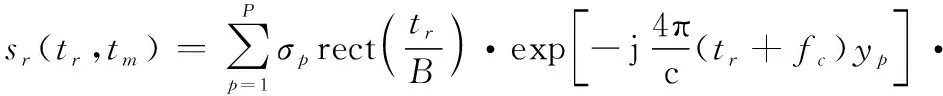
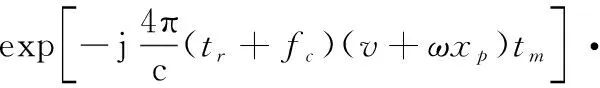
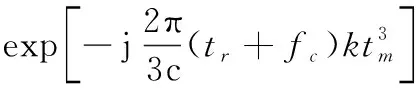
(8)

可见机动目标回波在慢时间域为多项式相位信号。

2 平动多项式参数估计

2.1 相位差分

尽管各散射点平动历程的一致性为平动参数估计带来了便利,但从式(8)可以明显看出,平动和转动对回波相位造成的影响在数学表达式上基本相同,这会使转动参数影响到平动参数的估计值。同时,对式(8)进行脉冲压缩后回波能量分布在多个距离单元也给平动参数估计带来了困难。

为了准确估计平动参数,采用相位差分的方法对回波进行处理:

(9)

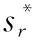
(10)

式中:=rect();(,)表示由相位差分造成的交叉项,设一个与散射点不同的散射点,则(,)可以表示为

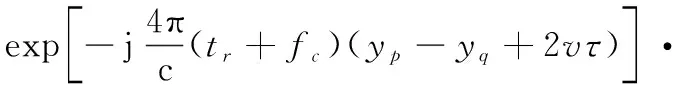
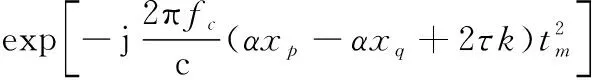
(11)

事实上,平动参数与转动参数虽然会对回波造成相似的附加相位,但二者的尺度存在很大的差异。例如,空中目标的速度通常在音速附近,即340 m/s,若目标速度与雷达视线方向的夹角为88°,则目标的径向速度约为11.8 m/s,而ISAR成像过程中,目标转动的总角度约为3°～5°,设ISAR成像总时间2 s,则目标转动速度约为0.035 rad/s,即便=10 m,的大小也仅有035,远小于目标径向速度。在进行相位差分处理时一般选取较小的时延常数,若=0.001 s,则式(10)中的仅有0.000 35,无论是对于包络还是相位,该参数的影响都是能够被忽略的,而平动参数远大于转动参数,因此其对回波相位的影响不能被忽略。综上,式(10)能够被近似为

(12)

对回波进行脉冲压缩,得到的结果为

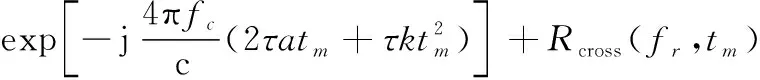
(13)

式中：为狄拉克函数。

2.2 基于LVD的平动参数估计

由式(13)可见,在进行相位差分处理后,回波的能量聚焦于=-4c对应的距离单元,取该距离单元的回波信号()用于平动参数估计,则()可以被表示为

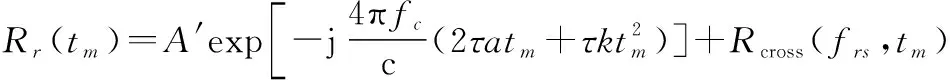
(14)

式中:

(15)

LVD具有良好的参数估计性能,且在信号存在多个分量时能够有效抑制交叉项对参数估计的干扰。LVD的核函数为

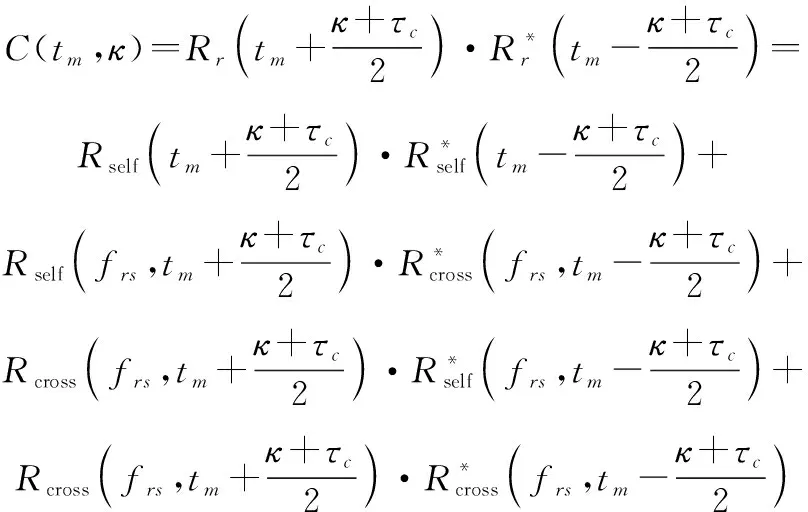
(16)

式中:表示时延变量;表示一常数;表示自项，即式(14)中除去(,)以外的部分。关于LVD交叉项抑制的原理,文献[30]给出了详细的分析,在此不再赘述。因此本节着重分析LVD变换中自项共轭相乘和(,)共轭相乘的结果。

用表示式(16)中自项共轭相乘的结果,其表达式为

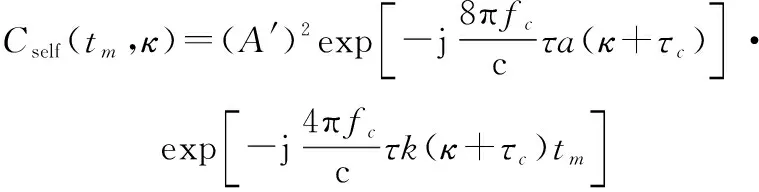
(17)

参考Keystone变换,设一个新的慢时间:

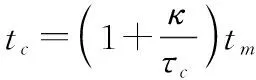
(18)

此时可写为

(19)

对式(19)在域和域同时进行傅里叶变换:

(20)

式中:FT 表示傅里叶变换;和分别为和经傅里叶变换后对应的频率。可见在进行LVD变换后,存在唯一峰值,且峰值位置仅和与有关。

对于(,),由于狄拉克函数仅在自变量取0时存在响应,因此(,)实际上仅包含满足=条件的交叉项,此时(,)可以被写为

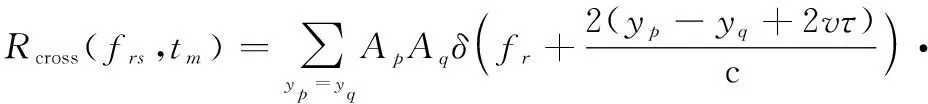
(21)

经过LVD变换后,式(21)变为

(22)

式中:

(23)

对于空间中两个不同的散射点,当其满足=时,必有-≠0,且当取不同的散射点和时,-也各不相同。式(22)经过傅里叶变换后,(,)的各个分量将分别形成尖峰且峰值位置各不相同。而在经过LVD变换后,所有分量的峰值都聚焦于同一位置,其幅度将远远大于(,)中任何分量。

根据以上原理,可以通过峰值搜索的方式得到平动参数的估计值:

{, }=argmax|LVD[()]|

(24)

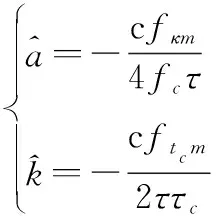
(25)

式中:表示峰值处对应的; 表示峰值处对应的;LVD[·]表示LVD变换。

利用平动参数估计值构造平动补偿函数,并对回波进行补偿:

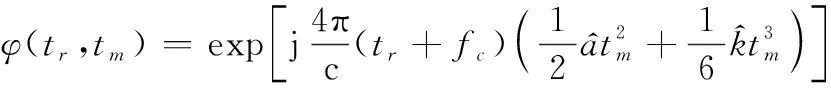
(26)

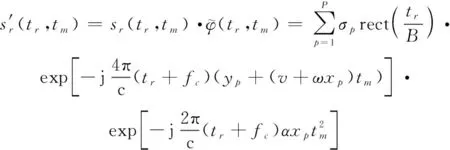
(27)

经过补偿后,平动加速度和平动二阶加速度对回波的影响已经被消除,仅剩平动速度对回波的影响依然存在。为了保证补偿精度,利用最小图像熵准则估计平动速度。首先构造平动速度估计函数:

(28)

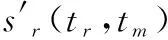
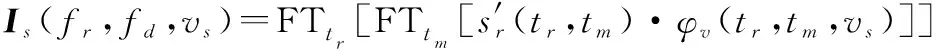
(29)

当=时,由平动速度造成的附加相位被完全补偿,此时信号在图像域的熵达到最小,根据此原理可以得到平动速度的估计值。图像熵的定义为

(30)

式中：表示图像对应的矩阵;和分别为矩阵的行数和列数。根据式(29)和式(30),对进行估计:

{}=argmin|EN((,,))|

(31)

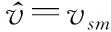
(32)

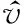
(33)

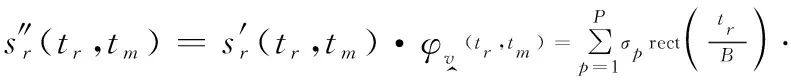
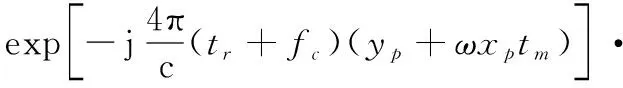
(34)

至此平动补偿已全部完成。

3 基于LVD的机动目标平动补偿流程

根据第2节的分析论证可以得出,基于LVD的机动目标平动补偿算法流程如下。

对回波(,)进行相位差分。

选出均方根值最大的距离单元的回波()。

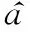
算法流程图如图2所示。

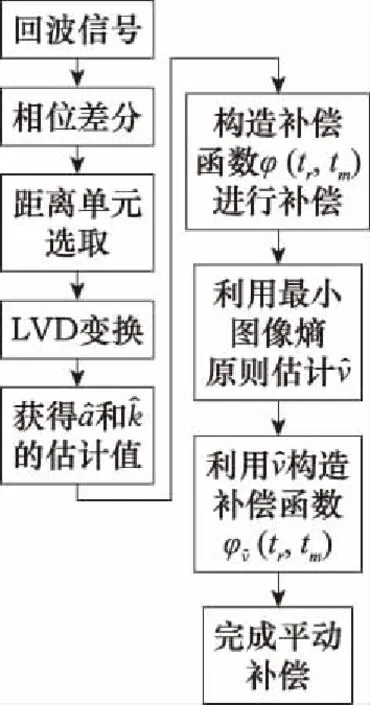
图2 流程图Fig.2 Flow chart

4 实测数据实验

利用yake-42实测数据对算法进行验证,该数据由中心频率5.52 GHz,带宽400 MHz,脉冲重复频率100 Hz的雷达测得,数据共含有快时间采样点数256点,慢时间采样点数256点。该数据RD成像的结果如图3所示。

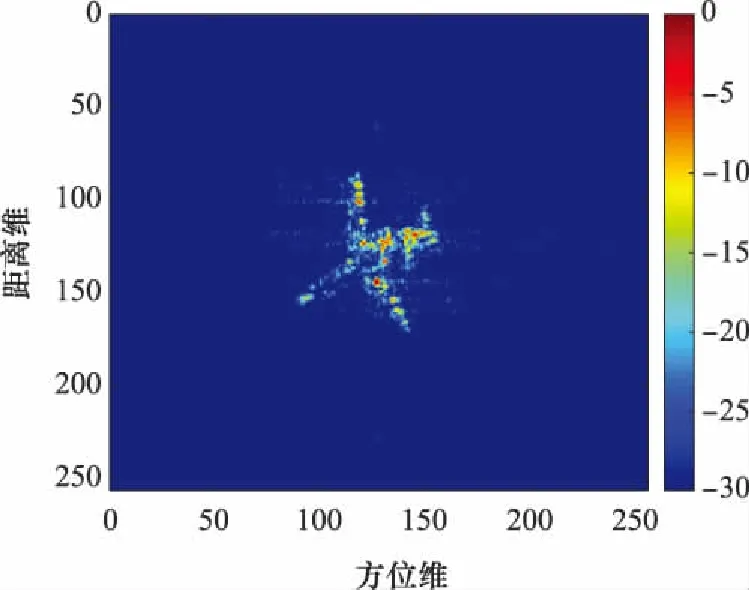
图3 实测数据yake-42的RD成像结果Fig.3 RD imaging results of measured data yake-42

对yake-42加入平动影响,平动参数分别为:=11.5 m/s,=7 m/s,=4 m/s。目标一维距离像如图4所示。

图4 含平动影响的一维距离像Fig.4 One dimensional range profile with translational effects

可见在添加了平动影响后,目标的距离像出现了显著的非线性弯曲。

对添加了平动的回波按照第3节给出的算法流程进行处理,并以图像形式给出主要步骤对应的结果:对回波信号进行相位差分,得到的结果如图5(a)所示;取能量最大的距离单元的回波进行LVD变换,得到的结果如图5(b)所示;构建平动补偿函数对平动加速度和平动二阶加速度补偿后得到的距离像如图5(c)所示;利用最小图像熵原则进一步补偿平动误差后的距离像如图5(d)所示;平动补偿后回波的RD成像结果如图6所示。

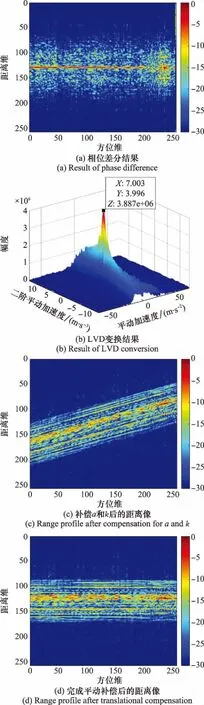
图5 主要步骤结果Fig.5 Results of main steps

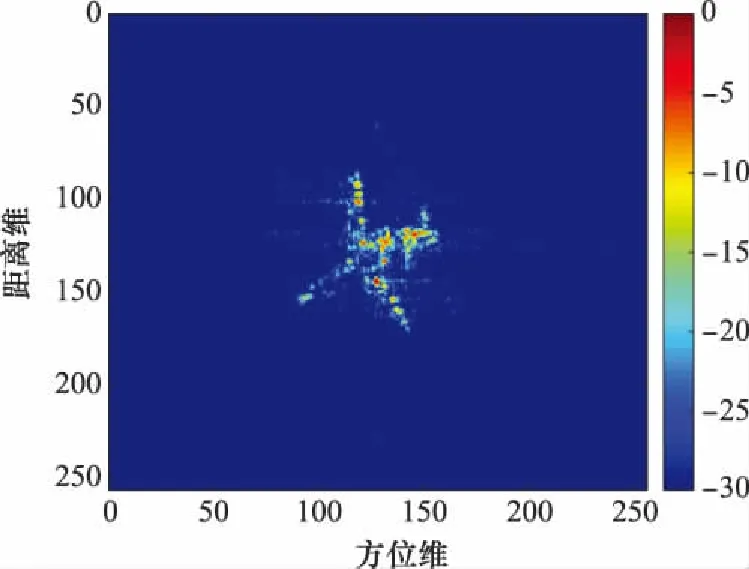
图6 平动补偿后RD成像结果Fig.6 RD imaging result after translational compensation

可见在经过相位差分处理后,回波能量都聚焦于同一距离单元,选择该单元的回波进行LVD变换,得到平动加速度和二阶平动加速度的估计值分别为7.003 m/s和3.996 m/s,与本实验设定值基本一致。利用上述参数补偿和对回波的影响后,回波距离像由非线性弯曲变为了线性弯曲,证明此时回波中仅剩下平动速度的影响未被补偿。利用最小图像熵原则对回波进一步补偿后,回波距离像变得平直,对采用本文方法进行平动补偿后的回波进行RD成像,其结果与图3基本一致。一系列实验证明本文方法能够有效实现对机动目标的平动补偿。

为了验证本文方法的优越性,采用图像质量评价指标-粒子群优化(image quality evaluation metric-particle swarm optimization, IQEM-PSO)算法和平均距离像相关+多特显点法作为对照组。在信噪比为-5 dB的环境下,各方法平动补偿后RD成像的结果如图7所示。

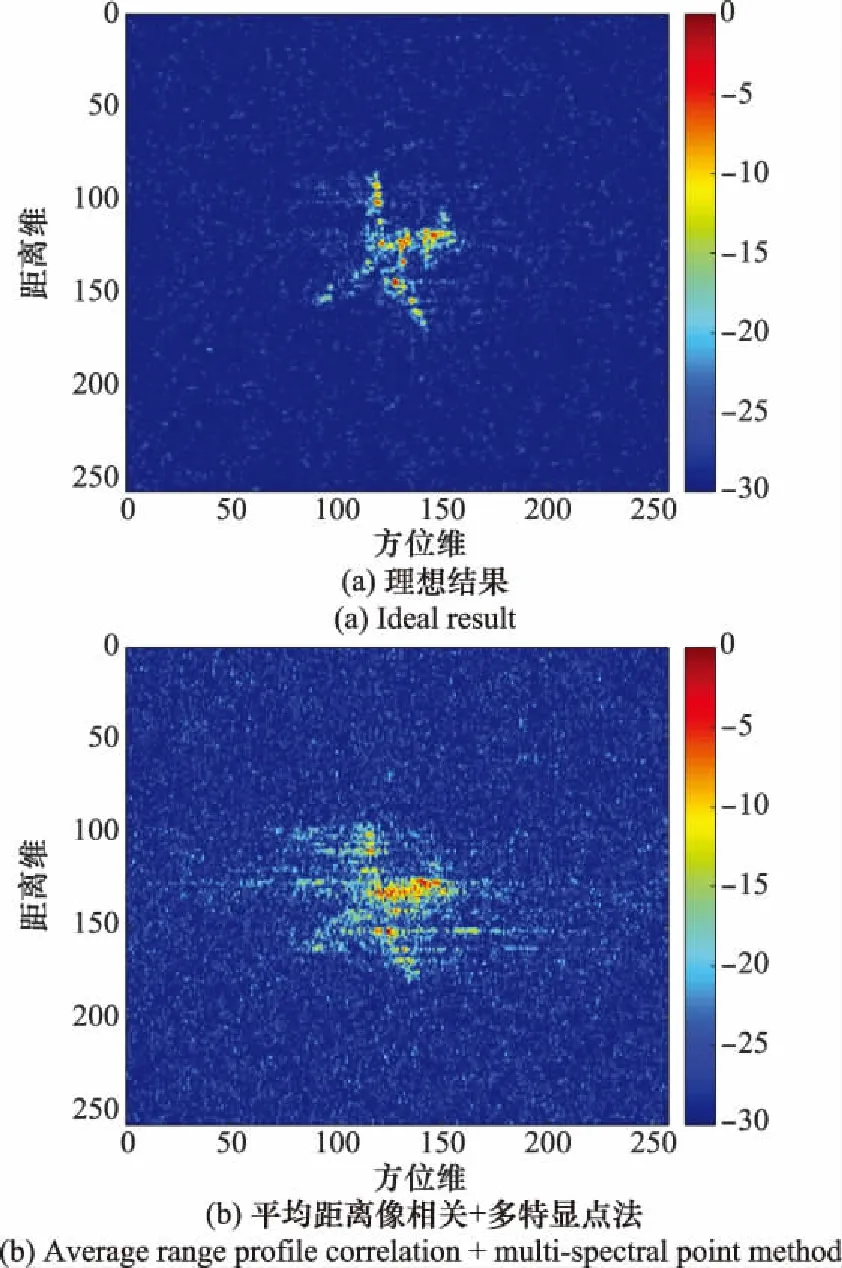
图7 不同方法结果对比Fig.7 Comparison of results for different methods

可见平均距离像相关+多特显点法的结果存在较为严重的散焦,说明对于低信噪比环境下的机动目标,采用平均距离像相关+多特显点法进行平动补偿难以获得理想的结果。IQEM-PSO方法的结果一定程度上优于平均距离像相关+多特显点法,但其依然存在散焦。这是由于IQEM-PSO在低信噪比环境下容易收敛于局部最优解。相比之下,采用本文方法进行平动补偿的结果聚焦良好,与理想结果十分接近。这证明了本文方法在低信噪比环境下具有较好的稳定性,并在性能上较传统方法更具优越性。

最后验证本算法在低信噪比下的性能。当信噪比分别为-6 dB,-9 dB,-12 dB时,利用本文方法得到的平动补偿结果如图8所示。

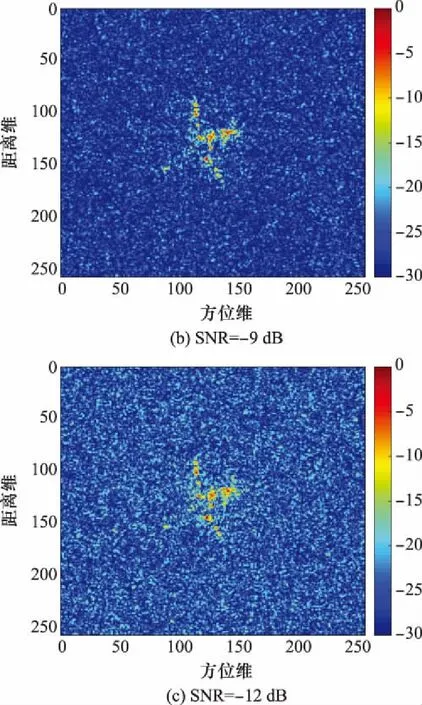
图8 低信噪比性能验证Fig.8 Performance verifications under low signal to noise ratio

可见在信噪比为-6 dB时,本文方法所得的结果除了噪声点幅度略微增强外,与图7(d)基本一致。当信噪比为-9 dB时,本文方法依然能有效补偿目标平动,但相比于图8(a),图8(b)中目标的方位产生了一定程度的偏移。当信噪比为-12 dB时,几乎难以分辨出目标和噪声,但根据幅度较大的几个散射中心来看,本文方法在-12 dB时依然能取得一定的效果。这足以说明本文方法在低信噪比环境下具有较好的鲁棒性。

5 结 论

本文提出了一种基于LVD的ISAR成像参数化平动补偿方法,以实现对机动目标稳定精确的平动补偿。该方法首先对回波进行相位差分来完成能量聚焦,而后利用LVD估计平动加速度和二阶平动加速度,并构造函数补偿二者对回波的影响,最后采用最小图像熵准则估计和补偿平动速度。实测数据实验证明了本方法的有效性,以及在低信噪比下的稳定性与优越性。