基于多分辨率显著性滤波的微动信号增强方法

唐明磊, 张文鹏, 姜卫东, 高勋章

(国防科技大学电子科学学院, 湖南 长沙 410000)

0 引 言

目标除主体平动之外的其他整体或部件的微运动,如旋转、进动、章动等,称为微动。目标微动能够对雷达回波信号产生额外的频率调制,反映目标的独特特征,包含目标几何结构、运动特性等更多的细节信息,为参数估计和目标识别提供了新的解决方案,有重要的应用价值。

微动目标雷达回波的微多普勒随时间非线性变化,因此采用频域分析方法不能够展示其频率的时变特性。时频分析使用时间、频率两个维度描述信号,能够刻画微动回波的时变多普勒调制特征,成为分析目标微动特性的主要工具。典型的时频分布包括线性时频分布短时傅里叶变换(short-time Fourier transform, STFT)、小波变换、S变换,二次Cohen类时频分布、魏格纳分布(Wigner-Ville distibution, WVD)、伪WVD(pseudo WVD, PWVD)等。现有分析微动特性的方法中,大部分是以时频图像为基础的,如基于线性调频小波基分解的微动部件回波分离、基于逆约旦变换的进动角估计、基于循环相关系数的微动周期估计等。因此时频图像的质量很大程度影响着特征提取和参数估计的精确度。

在实际场景中,微动信号容易受到其他信号的干扰,强噪声会使得微动信号在时频图像中难以分辨,严重制约了后续的微动特征提取和参数估计。目前,针对微动信号增强的研究非常少。文献[4]提出多重自相关法提取信号,在将信号从噪声中分离的同时,对信号进行增强。在时频域,文献[5]提到对信号进行奇异值分解,舍弃相对较小的奇异值后重构可达到降噪目的,但只能降低信号频谱之外的噪声。文献[6]利用生成对抗网络对时频图像进行去噪和增强处理,但只对单分量信号时频图进行了验证。因此,只能参考例如合成孔径雷达(synthetic aperture radar, SAR)图像、红外图像、医学影像等单通道图像的处理方法。主要有空域滤波算法(如均值滤波、中值滤波、非局部均值滤波、直方图均衡)、变换域滤波算法等传统算法,以及近年来兴起的基于网络的人工智能方法。图像显著性检测由于能够捕捉和突出显示图像中显著目标或区域,在SAR图像、红外图像中也得到了广泛的应用。

基于时频工具、空域滤波算法及已有显著性检测的方法及思想,本文提出了一种基于多分辨率显著性滤波的微动信号增强方法,在图像金字塔提供的多分辨率图像上分别计算时频图像的显著性并滤波,最后进行加权平均处理,有效地抑制了噪声,提升了时频图像的质量。实验结果表明,在-7 dB到7 dB的信噪比(signal to noise ratio, SNR)下,采用该方法均能显著提升时频图像峰值信噪比(peak signal to noise ratio, PSNR)。且在低SNR下,增强后的周期估计准确率有大幅提升。与其他几种典型空域滤波算法相比,该算法去噪效果更为显著且保持了较高的运算效率。

1 雷达回波模型

1.1 微动信号回波模型

采用文献[2]中的模型,如图1所示,其中LOS表示观测视线。设雷达发射频率为=10 GHz的单频连续波,锥体目标高2 m,底半径0.2 m,质心距底面中心0.4 m,进动频率=1 Hz,进动角设置为=25°,设雷达视线在参考坐标系中的方位角=220°,平均视界角=60°。

图1 进动锥体与观测雷达模型示意图Fig.1 Schematic diagram of precession cone and observation radar model

以雷达发射单频连续波为例,假设已进行平动补偿,则空间进动锥体目标的微动雷达回波信号为

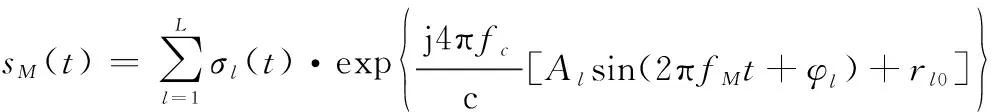
(1)

式中:()代表第个散射中心的幅度调制,当散射中心各向同性时为常数;第个散射中心相对主体的微动距离为

_()=sin(2π+)+0

(2)

可见,空间进动锥体的微动部分信号呈多分量正弦调频形式,调制频率等于目标进动频率,调制幅度和初相由散射中心的位置和进动角确定。

1.2 微动信号时频分析

对微动部分信号进行时频分析,采用STFT的方法得到其时频分布:

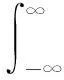
(3)

式中:()是关于=0对称的窗口函数。从式(3)可以看出,STFT的本质是,以滑窗的形式截取信号的片段来进行傅里叶变换,从而得到该段的频谱。取长短适中的窗长,使得时频图的时间、频率均有良好的分辨率。对信号进行离散化处理,采用65点长的汉明窗,傅里叶变换点数为2 048。不考虑锥体平动,根据第3节所设锥体进动参数,得到无噪时频图像。向其中加入-3 dB的高斯白噪声,则无噪时频图像及含噪时频图像如图2所示。

图2 无噪声及-3 dB条件下的时频图像Fig.2 Time-frequency image without noise and under -3 dB condition

可以看到,在-3 dB条件下的时频图像中,背景区域存在大量杂斑,且随机分布。与噪声相比,虽然微动信号的像素值依然相对显著,但给识别微动信号增加了一定难度。

2 基于多分辨率显著性滤波的微动信号增强

一般情况下,高斯白噪声频率丰富,在整个频谱上都有成分,功率谱密度相对较低;而平动补偿后的微动信号频谱范围较集中,功率谱密度相对较高。因此,即使SNR一定范围内较低时,在频域有限的时频图中,微动信号曲线相比于噪声背景依然较显著。这启发我们基于像素块间的欧氏距离计算显著性的方法处理时频图像,检测并突出图像中的显著区域。算法流程如图3所示。

图3 算法流程Fig.3 Algorithm flow

2.1 筛选背景区域及选择参考背景块

将整个时频图以图中像素值最高点归一化,则整个时频图所有像素值在0～1内变化。将时频图均匀划分为×的图像块,记为(),其中可调整大小。逐块计算每一个×块的像素平均值,记为()。所有()中值记为。当()<,对应的()块视为背景区域块,否则视为显著区域块。因为时频图像中占大部分的为背景区域,所以选择中值作为背景区域块的筛选门限是合理的。将所有的背景区域块用表示。以=8和=16为例,背景区域筛选情况如图4所示(红色矩形框所示为背景区域块)。

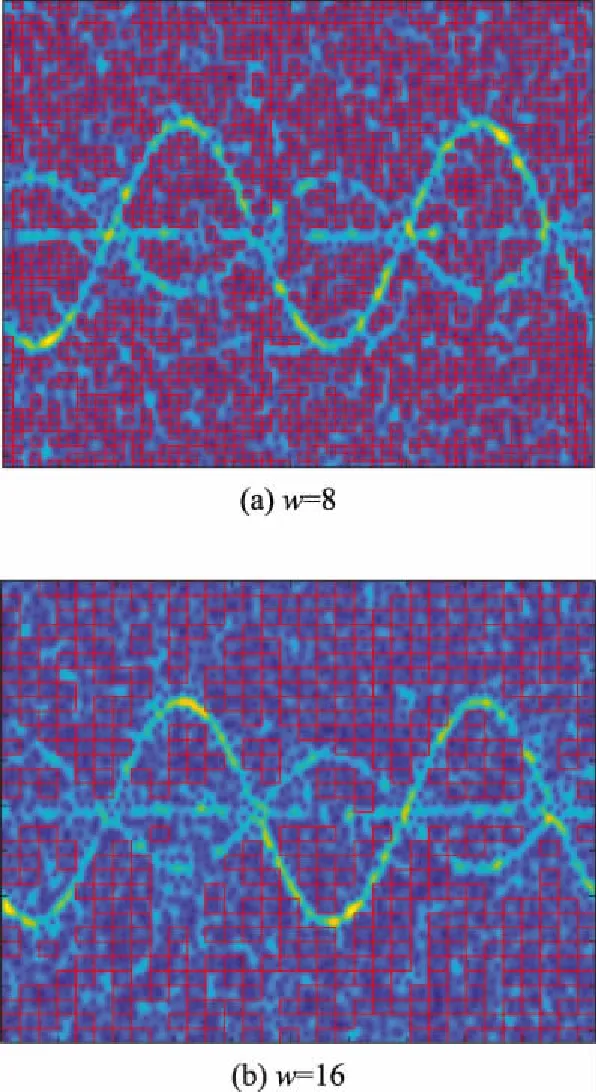
图4 -3 dB时的背景区域筛选情况Fig.4 Background area screening at -3 dB

在计算局部显著性时,如果将当前块与所有背景块逐个比较差异,则计算量非常大。为提高计算效率,在所有背景区域块中随机选择个作为参考背景块,记为,其中的第个记为Ref(),则有:

={Ref()|∈[1,],Ref()∈}

(4)

由于所加噪声为高斯白噪声,因此各背景区域块噪声独立同分布,随机选择其中的个作为参考背景块是合理的。

2.2 计算显著性图像

文献[19]采用逐个像素点计算显著性的方式,运算量相对较大。在本文中,以块为单位计算得到显著性,将该显著性值赋给该块的所有点,使得显著性计算这一项的计算效率增加了倍,同时图像增强的效果不会发生明显的退化。

根据第21节选择参考背景块的方法,将划分好的时频图像的每一图像块的×个像素与参考背景块的×个像素逐像素计算距离,最后得到两个块的欧式距离。以当前图像块()为例,计算公式为

(5)

式中:,分别为各块中对应像素的坐标值。基于()与个参考背景块Ref()之间的欧氏距离,计算得到()块的局部显著性如下:

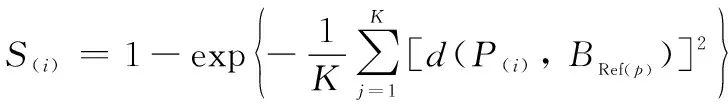
(6)

可见,若()与Ref()之间欧式距离越大,则式(6)中的指数项越接近于0,局部显著性()越接近于1。()就越有可能为信号占据的显著区域块。

当=4,=4时,逐块计算所有()的(),得到整幅时频图像的显著性图像,如图5所示。

图5 -3 dB时的显著性图像Fig.5 Saliency image at -3 dB

可见,信号区域的显著性最强,但由于存在较强的噪声,背景中也有大量显著的亮斑,为增强图像质量,因此需要进一步处理。

2.3 多分辨率显著性滤波

多尺度框架在图像分析与处理中得到了广泛的应用。图像金字塔是一种以多分辨率来解释图像的结构,通过下采样生成层不同分辨率的图像。以金字塔形状排列,最高分辨率的图像置于底层,往上是一系列分辨率逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔,如图6所示。

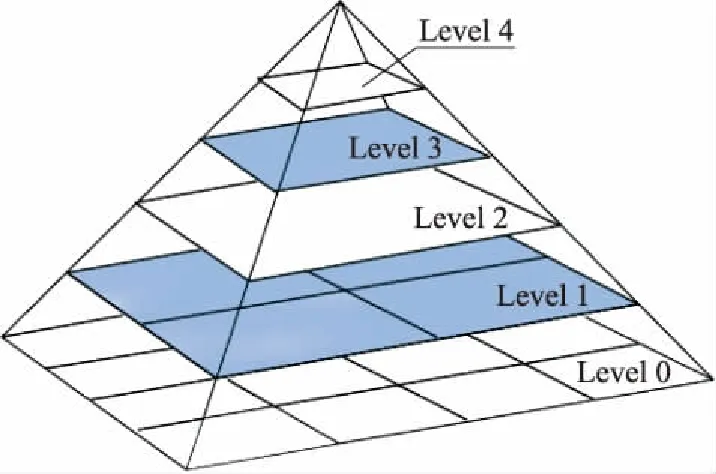
图6 多分辨率图像金字塔结构Fig.6 Image pyramid structure with multi-resolution

如果研究对象尺寸较小或对比度较低,那么需要以较高的分辨率来研究它们;如果尺寸较大或对比度较高,则以低分辨率进行粗略的观察就已足够。即图像分辨率越低,细节就越少。对于时频图像,高分辨率下信号细节特征得以保留,但同时强噪声依然存在;而低分辨率条件下,背景区域的噪点作为尺寸较小细节部分被忽略掉,同时微动信号保留了粗略的轮廓特征,但细节丢失严重。

基于以上原理,将时频图像在多分辨率进行处理,以=4为例,计算得到第层分辨率图像的显著性图像如图7所示。

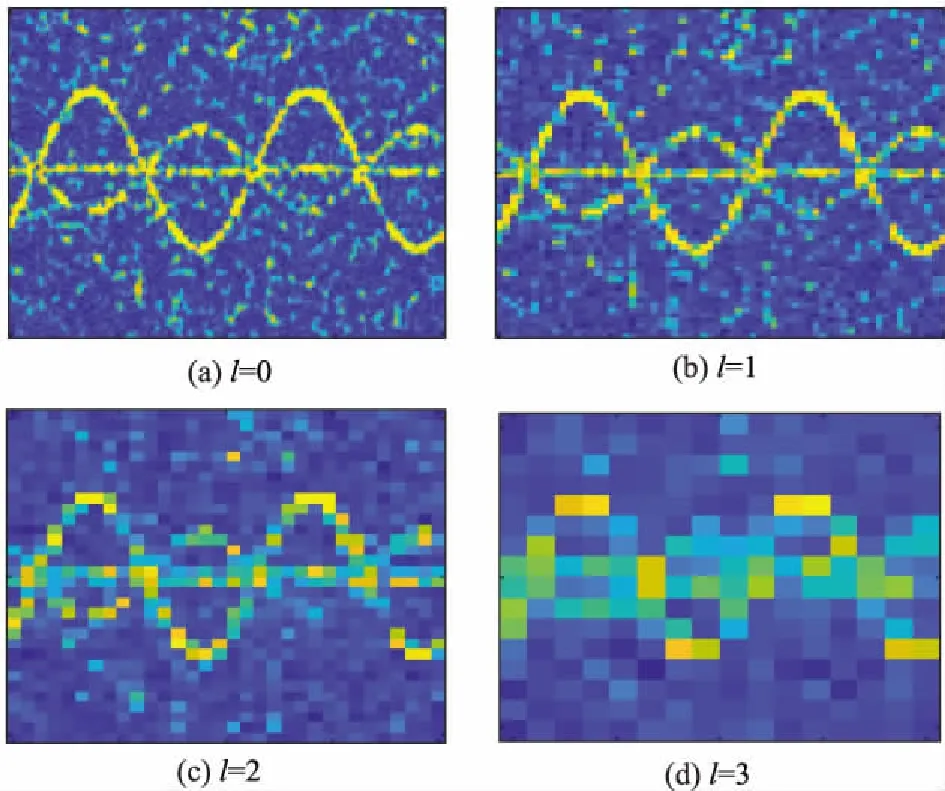
图7 4层的显著性图像Fig.7 Saliency images of four layers

表示时频图中不同部分的显著性,其像素在[0,1]内取值。信号区域显著性强,其()值更接近1,背景区域显著性弱,其()值更接近0。因此将显著性图像视为“滤波器”,与该层时频图像进行对应点乘运算,信号区域像素与接近于1的()相乘得到较好的保留,而背景噪声区域与接近于0的()相乘更加被抑制。得到每层的滤波输出图像:

_out=⊙

(7)

式中:为第层时频图像;为第层时频图像的显著性图像;_out为第层滤波输出图像。图8(a)～图8(d)分别显示了-3 dB时的4层输出图像。

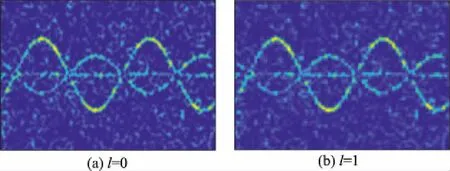
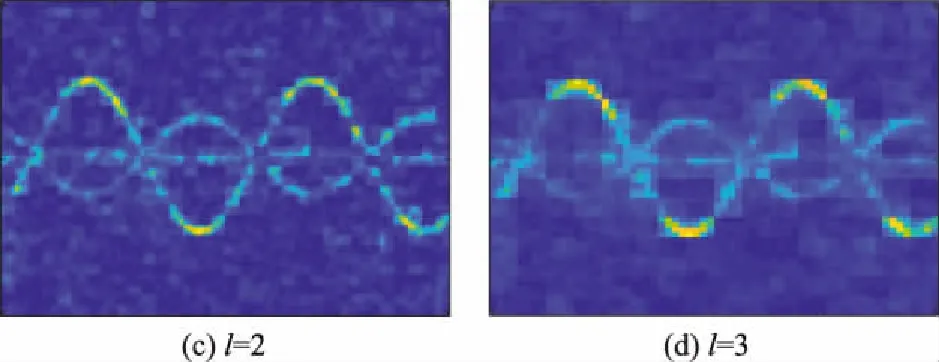
图8 4层的滤波输出图像Fig.8 Filtering output images of four layers

对比图7,显然每层的滤波输出图像比该层的显著性图像抑制噪声效果更好。将每层的滤波输出图像求加权和后得到最终的输出图像:

(8)

式中：表示与层数相关的权重,定义为

(9)

随着层数的增大分辨率降低,信号区域特征得以保留,背景噪声变得不那么突出。最终增强输出图像如图9所示。该算法在信号显著性保留和噪声抑制之间取得了很好的折衷。

图9 增强后输出图像Fig.9 Output image after enhancement

3 实验分析

3.1 仿真模型

采用第1.1节中的模型。考察锥体顶点P1(0,0,1.6)和底部边缘散射点P2(0,-0.2,-0.4) P3(0, 0.2,-0.4)的回波特性,设置P1点散射强度为1,P2、P3点散射强度为0.7,采样频率PRF=1 024 Hz,并在回波中加入高斯白噪声。本文中为提高运算效率,首先将原始时频图缩放到512×512的分辨率,再进行后续处理。

3.2 参数设置

本文所采用算法涉及多个参数,下面探讨几个主要参数(参考背景块边长为,参考背景块个数为,图像金字塔层数为)的设置及影响。

PSNR是信号最大功率与信号噪声功率之比,是最普遍、最广泛使用的评鉴画质的客观量测法,计算方法如下:

(10)

(11)

式中:MAX为图像的最大像素值,在灰度图中范围为(0,255)。在本文中,归一化到(0,1)内处理,则MAX=1。MSE为与无噪时频图像的均方误差(mean square error, MSE)。本文用增强前后时频图像的PSNR增益衡量时频图像的质量改善:

ΔPSNR=PSNR-PSNR

(12)

设SNR=-3 dB,经100次蒙特卡罗仿真,得到最佳参数分别为=4,=4,=4,验证过程如下。

(1) 在给定的=4,=4时,设定在1～12内变化,如图10所示,输出图像质量呈先增加后下降的趋势,最大PSNR增益在=4时得到。原因是如果参考背景块尺寸太小,不能很好地捕捉背景的实际特征。某些噪声可能非常强,以至于所在局部背景块的平均值也非常大,这可能使得这些块被认定为显著区域而不是背景区域。如果参考背景块尺寸太大,可能会导致以背景区域块覆盖许多属于信号的像素,这也会导致参考背景块划分不当。若待处理时频图的分辨率不同,则应相应改变的值。

图10 PSNR增益随w变化情况Fig.10 Gain of PSNR varies with w

(2) 给定=4,图像增强的质量与相关。采用多层显著性滤波图像融合的效果比简单地采用单个尺度的显著性滤波图像对斑点噪声具有更强的鲁棒性。由于在不同分辨率下不变,因此对于层数较高的图像,的取值会因为相对过大,筛选出的背景块包含了过多信号区域的像素点，也会导致参考背景块划分不当。如图11所示,当固定且设置为4时,图像增强的质量优于其他不同参数设置的图像。

图11 PSNR增益随L变化情况Fig.11 Gain of PSNR varies with L

(3) 将和分别设置为4和4,并将整数从1变为12,然后得到图12所示的结果。随着的增加,图像增强的质量逐渐提高,当大于4时,这种改善并不显著。直观的理解是:当参考背景块数量增加,有利于捕捉背景的特征。然而,过多的参考背景块也意味着更多的计算冗余,使得效率大大降低。事实上,对于大多数含噪时频图像,背景中的杂斑是静止且独立同分布。因此,用若干参考背景块代替所有背景区域块进行显著性计算是可行的。

图12 PSNR增益随K变化情况Fig.12 Gain of PSNR varies with K

综上所述,参数设置的一个建议方案是为4,为4,为4。

3.3 不同SNR下的PSNR增益

取=4,=4,=4,经过100次蒙特卡罗仿真,在SNR为-7～7 dB时,PSNR增益如图13所示。

图13 不同SNR下增强后的PSNR增益Fig.13 Enhanced PSNR gain under different SNRs

以SNR=-3 dB、0 dB时为例,时频图像增强前后如图14所示。

图14 增强前后时频图像对比Fig.14 Time-frequency image comparison before and after enhancement

可见,该算法在噪声抑制和信号保留方面都取得了比较好的效果。

3.4 微动周期估计验证

主要验证低SNR条件下的改善效果。采用文献[3]中基于循环相关系数的微动周期估计方法,来验证采用本文方法增强后微动周期估计效果的改善。随机生成2 000组SNR为-7～0 dB的信号,经过STFT后,首先对含噪图像直接估计微动周期,然后采用本文方法进行增强处理后,估计微动周期。周期估计相对误差在5%以内视为估计准确,则增强处理前后,微动周期估计的准确率、均值、MSE、平均绝对误差(mean absolute error, MAE)分别如图15(a)～图15(d)所示。

图15 增强前后估计准确率、均值、MSE、MAE对比Fig.15 Comparison of estimation accuracy, mean value, MSE and MAE before and after enhancement

可见,在SNR低于-3 dB时,增强后估计准确率、均值、MSE、MAE均有明显改善,效果约相当于增加SNR 2 dB。

3.5 实测数据验证

使用雷达测量数据来验证本文方法的有效性。锥体弹头模型同第1.1节,进动周期=2 s。其回波雷达截面积数据由暗室测量得到,回波时频图像如图16所示,雷达回波采样频率PRF=200 Hz。在暗室测量回波的基础上添加-7～7 dB的高斯白噪声。取=4,=4,=4,以-3 dB、3 dB为例,增强前后时频图像如图17所示。

图16 暗室弹头回波时频图像Fig.16 Time-frequency image of anechoic chamber warhead echo

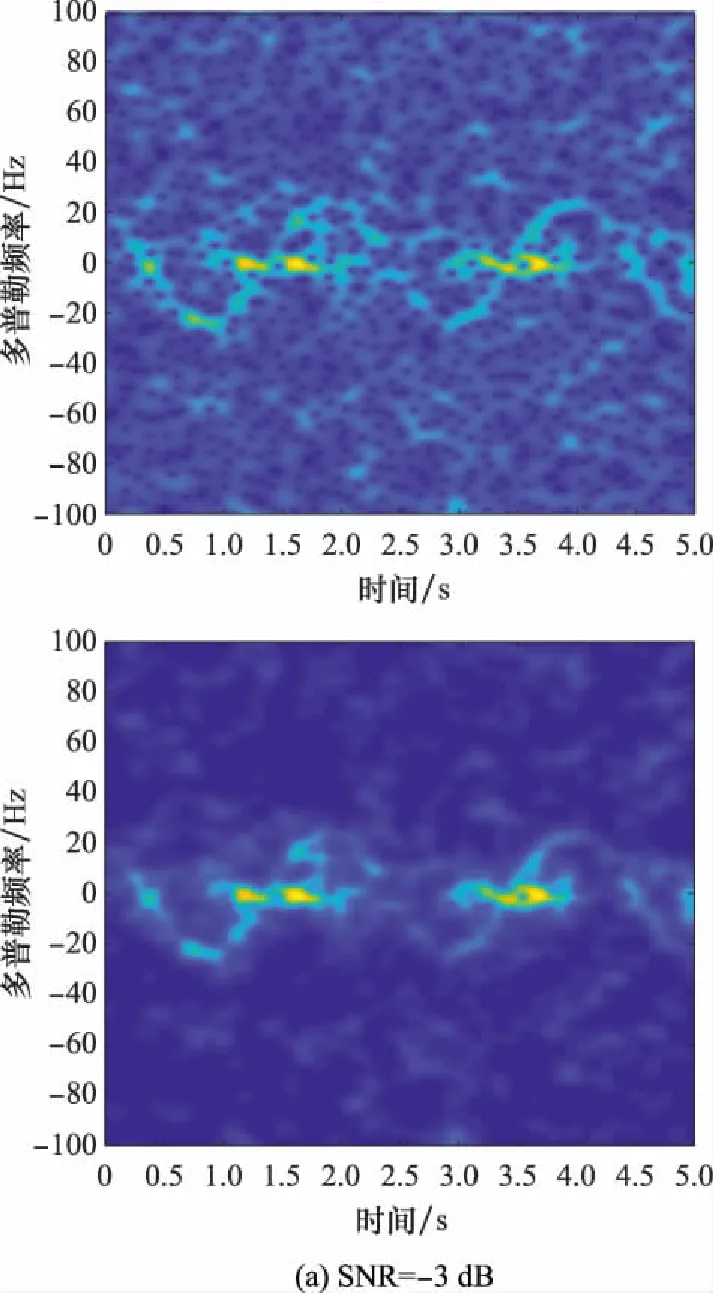
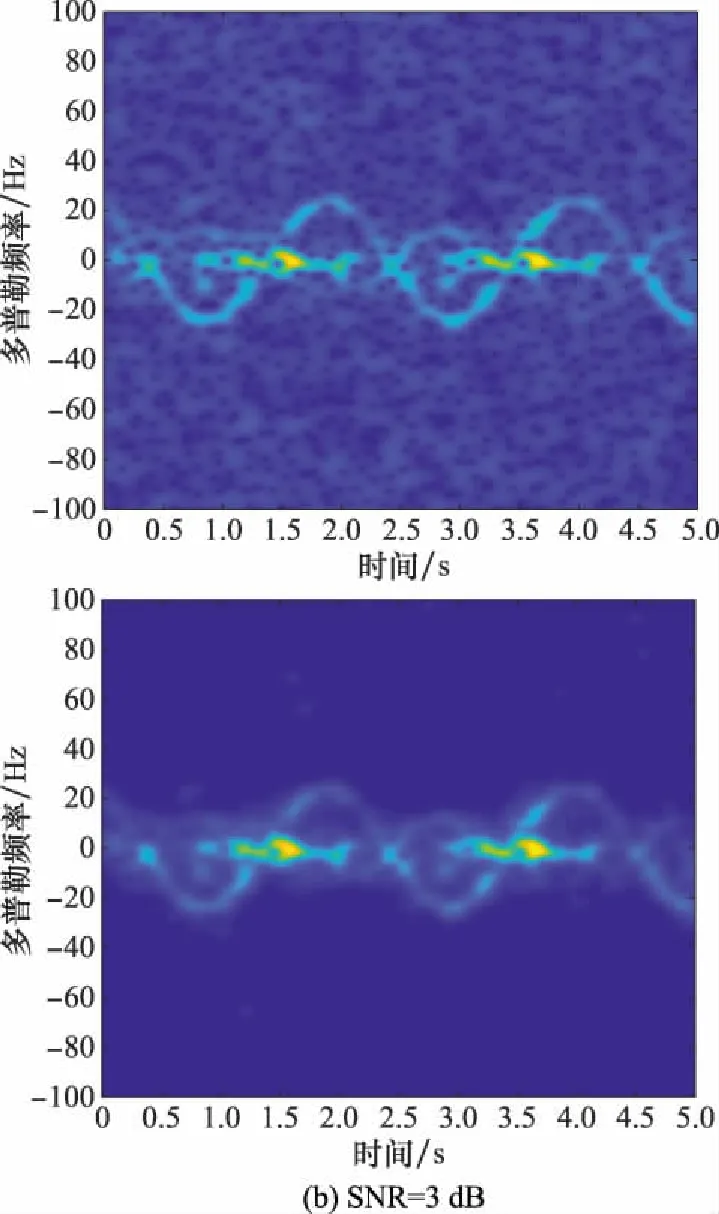
图17 增强前后的暗室弹头时频图像Fig.17 Time-frequency images of anechoic chamber warhead before and after enhancement

经过100次蒙特卡罗仿真,在-7～7 dB的SNR下,增强后的PSNR增益如图18所示。其中在0 dB以下的低SNR条件时,PSNR增益均达到了6.5 dB以上,可见,图像质量得到了明显提升。

图18 暗室弹头不同SNR下增强后的PSNR增益Fig.18 Enhanced PSNR gain of anechoic chamber warhead under different SNRs

进行200次蒙特卡罗仿真,使用循环相关系数法对SNR在-7～0 dB条件下增强前后的时频图像进行微动周期估计,要求周期估计相对误差在15%以内。则增强处理前后,微动周期估计的准确率、均值、MSE、MAE分别如图19(a)～图19(d)所示。

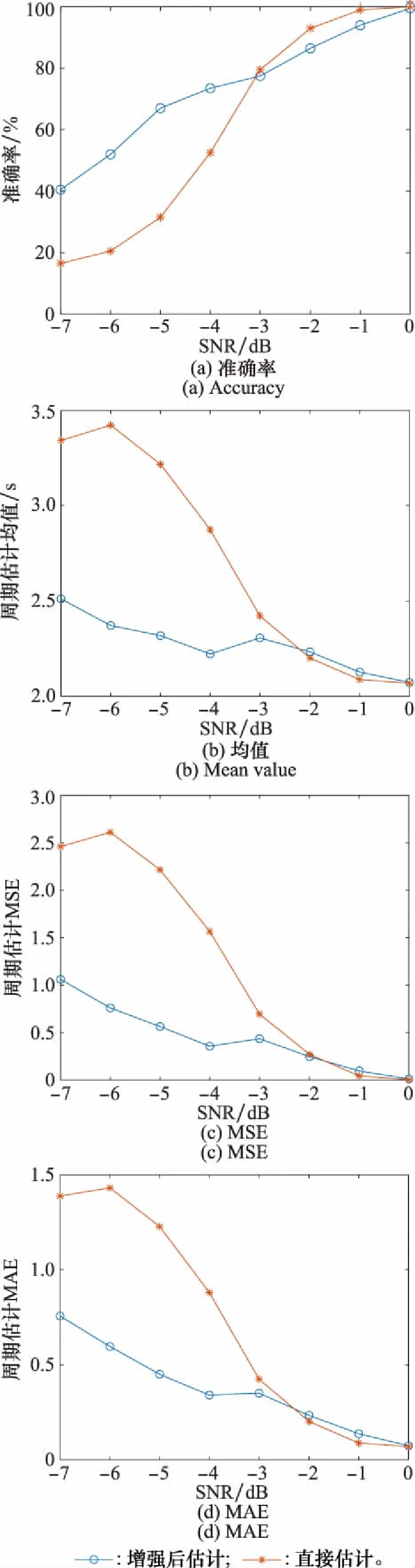
图19 暗室弹头增强前后估计准确率、均值、MSE、MAE对比Fig.19 Comparison of estimation accuracy, mean value, MSE and MAE before and after enhancement of anechoic chamber warhead

实验结果与仿真实验相似,在SNR低于-3 dB时,增强后估计准确率、均值、MSE、MAE均有明显改善,再次证明了本文所提算法的有效性。

3.6 算法对比

采用第3.1节仿真模型,将所提算法的实验结果与几种经典空域滤波算法进行对比,包括均值滤波(核半径为7)、中值滤波(核半径为7)、高斯滤波(核半径为9,方差为4)、非局部均值滤波(邻域半径为8,搜索窗半径为12,平滑参数为4)。以-3 dB SNR为例,增强后的图像如图20所示,与图9相比,显然在视觉上本文所提算法能更好地抑制背景噪声,突出信号区域。

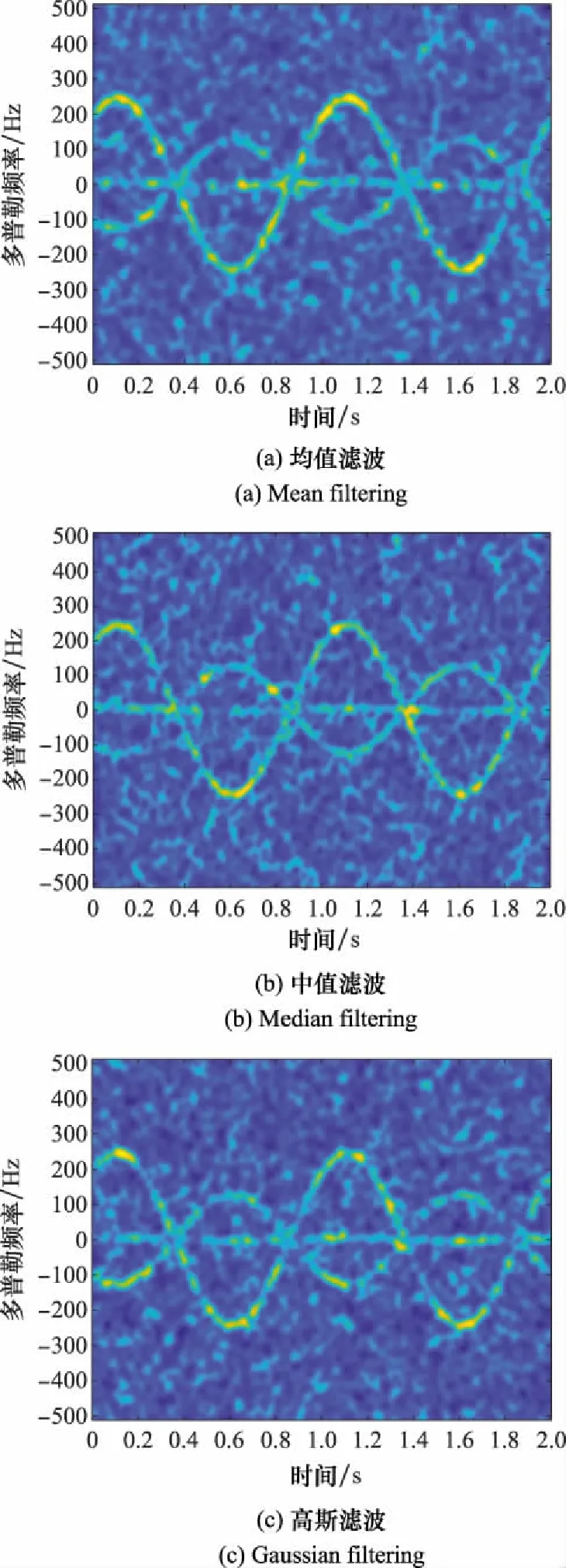
图20 -3 dB下不同滤波算法的去噪效果Fig.20 Denoising effect of different filtering algorithms at -3 dB

在-7～7 dB的SNR下,不同算法增强后的PSNR增益如图21所示。可见在不同SNR下,本文所提算法的PSNR增益远高于其他算法,去噪效果更优。

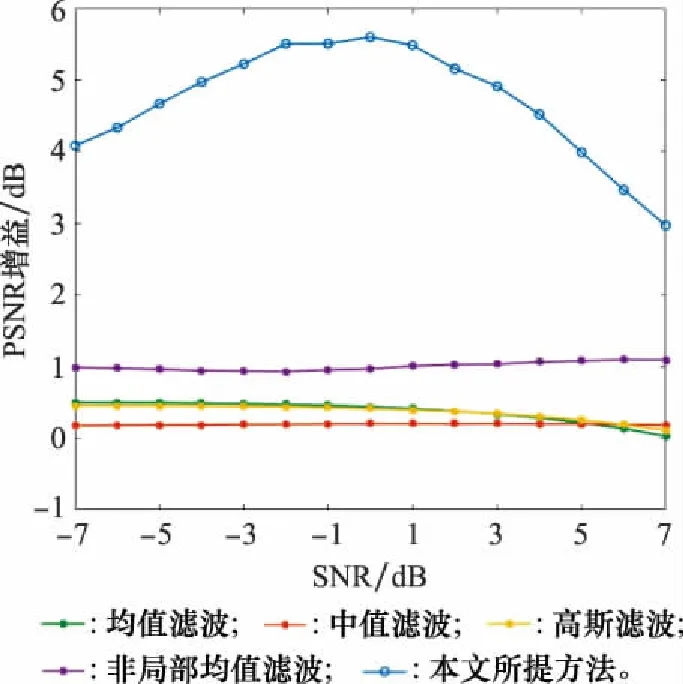
图21 不同滤波算法的PSNR增益对比Fig.21 Comparison of PSNR gain of different filtering algorithms

在运行时间方面,本文所提算法在保持最好的去噪效果同时,亦能保持较高的运算效率,处理实时性较好。

表1 算法运行时间比较Table 1 Algorithm run time comparison s

4 结 论

本文针对低SNR下微动信号增强问题进行研究,分析了微动信号时频图像的特点,提出基于多分辨率显著性滤波的微动信号增强方法。通过仿真实验和实测数据的处理结果表明,采用该方法能够有效抑制噪声,提升时频图像的微动信号的质量。SNR为-3 dB以下时,基于增强后时频图像的微动周期估计准确率大幅提高。与几种典型的空域滤波算法进行比较,在去噪效果上具有明显优势的同时也保持了较高的运算效率,因此可作为一种有效的微动信号增强途径。本文尚存在许多不足之处,比如:不同SNR下最佳参数可能会不同,对此并未多加验证;只验证了3个主要参数的影响,尚未探究其他参数(如每层的缩放比例、权重等)的影响;当主体回波较强时,可能会导致微弱的微动回波分量被淹没或被误判背景区域。接下来将会进一步改进探索并探索新的方法。