基于交互多模型的分组δ-广义标签多伯努利算法
2022-04-07辛怀声
辛怀声, 曹 晨
(中国电子科技集团公司电子科学研究院, 北京 100041)
0 引 言
在多目标跟踪(multiple target tracking, MTT)技术的发展过程中,以数据关联算法为核心的方法是一类经典技术路线,代表算法有最近邻关联、概率数据关联、联合概率数据关联、多假设跟踪。此类方法的本质是通过数据关联将MTT问题分解为单目标跟踪问题。目前这类算法已经在雷达跟踪系统中得到了应用。
近年来以有限集统计为基础发展起来了另一类MTT理论。在该理论框架下目标状态和传感器量测都由随机有限集(random finite set, RFS)进行描述建模,并构建最优多目标贝叶斯滤波器,为MTT问题提供了严谨、统一、坚实的理论基础。这类算法的代表有概率假设密度(probability hypothesis density,PHD)、集势PHD(cardinalized PHD, CPHD)以及CBMeMBer(cardinality balanced multiple target multi-Bernoulli)滤波器。基本PHD、CPHD和CBMeMBer适用于点迹过滤,多目标状态不包括标签,不做航迹跟踪。优势是计算复杂度较低,以PHD为例计算复杂度仅为()。文献[11-12]在随机有限集理论的基础上,结合数据关联思想给出了多目标贝叶斯滤波器的精确闭式解,也称为Vo-Vo滤波器及其δ-广义标签多伯努利(δ-generalized labeled multi-Bernoulli,δ-GLMB)版。GLMB滤波器是第一个可以被证明的多目标最优贝叶斯滤波器。
为了提高GLMB滤波器的计算效率,文献[13]提出标签多伯努利(labeled multi-Bernoulli,LMB)滤波器,LMB作为δ-GLMB的一种近似解,将分组计算思想引入了GLMB滤波器领域,大幅提高了δ-GLMB的计算效率,但是目标跟踪精度稍逊于标准δ-GLMB滤波器。为了提高GLMB的航迹跟踪精度,文献[14]利用威沙特分布近似处理量测协方差矩阵。文献[15-16]引入改进型卡尔曼滤波以提高滤波器在非线性情况下的适应度。文献[17]则改进自适应新生目标航迹起始方法,提高算法的目标数量估计精度。文献[18-19]将马尔可夫跳变系统(jump Markov system,JMS)引入GLMB领域,给出JMS-GLMB或多模型Vo-Vo(multi-model Vo-Vo, MM-Vo-Vo)滤波器,提高了GLMB对机动目标的跟踪精度。文献[20]则给出了LMB版本的多模型机动目标跟踪滤波器。然而上述算法都没有将分组计算和JMS相结合,本文在δ-GLMB滤波器的基础上结合航迹分组思想对多目标状态集合和观测集合进行分组化处理,另外引入JMS对目标状态进行扩展,参照交互多模型(interacting multiple model,IMM)近似算法给出基于IMM的分组δ-GLMB(IMM based grouping δ-GLMB, IMMG-δ-GLMB)滤波器的预测和更新递推方程。
文章的第1节介绍基本GLMB算法。第2节给出针对目标状态和观测的分组方法,对影响分组的因素进行分析,之后引入JMS对多目标状态进行扩展,并根据IMM算法对JMS-GLMB进行近似处理,推导出IMMG-δ-GLMB的预测和更新递推方程以及高斯混合实现方式。第3节设定两组仿真实验,第一组实验设定一个常见的多目标场景,对IMMG-δ-GLMB、δ-GLMB以及JMS-GLMB的MTT性能进行对比,第二组实验则设定一个密集编队场景,对不同分组条件下IMMG-δ-GLMB跟踪密集多目标时的分组滤波效果进行比较分析。第4节进行评价和总结。
1 δ-GLMB滤波算法
本文符号定义采用Mahler在文献[7]中的定义方式:
定义航迹集合为={(,),(,),…,(,)},||=,其中~分别表示航迹标签,用于标识不同的航迹身份。


定义(,)为目标存活概率密度函数。
定义|(-|)为均值为|,协方差矩阵为|的多维高斯分布密度函数。
定义量测集合为={,,…,}。~表示传感器获取的目标量测。


1.1 δ-GLMB滤波器的时间预测
给定时刻多目标状态的先验分布密度函数为

(1)

预测步骤的表达式如下所示:

(2)
式中:

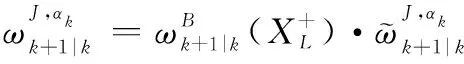




1.2 δ-GLMB滤波器的量测更新
考虑标准点目标量测模型,每一个目标以概率(,)被探测到,被探测到后生成一个量测点,对应的量测似然度表示为(|,)。量测集中不仅有目标形成的量测点,还包括杂波点(虚警点),虚警点构成一个泊松RFS,强度函数为()。在上述假设下,量测更新步骤后生成的后验密度仍然是δ-GLMB。
给定+1时刻量测集合为+1,相应的多目标后验分布可以表示为
+1|+1(|+1)=||,||·

(3)
式中:

(1-0,())(,)×+1(()|(,))(())






2 IMMG-δ-GLMB滤波算法
本节首先给出航迹与量测的分组方法,之后基于IMM计算框架推导IMMG-δ-GLMB算法的预测和更新表达式。
2.1 航迹与观测分组
航迹与量测关联新息可以表示为

(4)
式中:为状态转移矩阵;为观测矩阵;为状态转移过程噪声矩阵;为观测协方差矩阵。记矩阵:

则新息可以重新写为

(5)
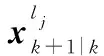
对于一个随机有限集来说,如果∃,∈,使得()=()>0,且≠,根据关联函数的定义有(,)<且(,)

(6)
式中:为航迹组,且∩=∅,≠。另外,定义函数的逆函数形式如下:

(7)
假设对于两个航迹组和,如果存在某个量测与两个航迹组分别能够关联,即

且

也就是说航迹组和存在共享观测,则航迹组和可以合并为一个航迹组,即=∪,且观测集合也可以对应合并,即

(8)
最后,观察矩阵的表达式可知航迹组的划分与目标距离、方位和俯仰误差、扫描周期以及马尔可夫运动模型参数有关。通过调整参数组合使得||越小,则对应的,就越大,这样不同航迹关联同一量测的可能就越小,航迹组划分越精细,航迹组数量越多。反之,则航迹组划分越粗糙,航迹组数量越少。因此可以预计两种极限情况,第一种极限情况下,每一个航迹组内只包含一个目标,此时分组δ-GLMB(grouping-δ-GLMB, G-δ-GLMB)会转化为单假设跟踪(single hypothesis tracking, SHT),此时每个航迹组内的唯一目标要么只能与一个量测关联,要么没有量测与之关联,航迹组的每次时间预测迭代能够产生的分支也只能有两条,即目标下一周期继续存在或者不存在两种情况。第二种极限情况是所有目标都处于一个航迹组,此时G-δ-GLMB退化为普通δ-GLMB。
2.2 IMMG-δ-GLMB时间预测


(9)
另外,给定马尔可夫模式跳变概率矩阵为

(10)
式中:, 表示模式跳变到模式的概率。对马尔可夫状态转移密度函数使用条件概率规则可以得到马尔可夫跳变状态转移函数:

(11)
另外,根据全概率公式,目标的状态分布可以写为

(12)
式中:为目标处于模式的概率。由于不同航迹组之间相互独立,所以分组多目标分布的先验分布可以表示为



(13)
式中:为分组索引。
根据IMM的状态分布混合方程有:

(14)
则经过状态混合后的多目标分布为


(15)
式中:









(16)
对经过状态混合后的多目标分布式(16)进行时间预测,得到的多目标时间预测分布密度函数可写为


(17)
式中:





2.3 IMMG-δ-GLMB的量测更新
经过观测滤波后,多目标后验分布仍然可以表示为各个航迹组GLMB分布的乘积,保证滤波迭代的封闭:


(18)
式中:


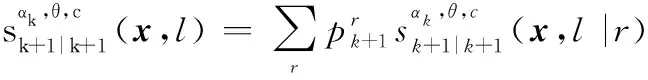



IMMG-δ-GLMB的模式概率更新方程如下:

(19)

2.4 IMMG-δ-GLMB的高斯混合实现
在假设目标新生模型、运动模型、观测模型都满足线性高斯条件,并且目标存活概率和目标探测概率都是常数后,可以得到IMMG-δ-GLMB的高斯混合递推公式。
根据式(17),多目标时间预测分布密度函数可写为


则在线性高斯条件可以得到








按照式(18),观测更新可以写为


则在线性高斯条件下有

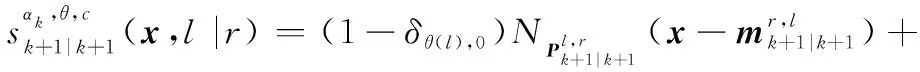




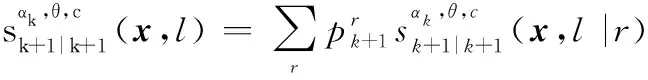



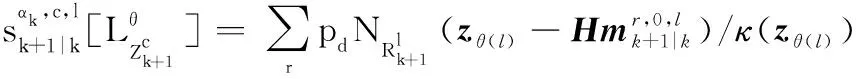

观测更新后目标状态提取方程为

(20)
对应的协方差矩阵为


(21)
根据式(19),线性高斯条件下IMMG-δ-GLMB的模式概率更新方程如下:

(22)

3 仿真与结果分析
3.1 仿真场景1
设置一个两维跟踪场景,比较δ-GLMB、JMS-GLMB和IMMG-δ-GLMB的MTT性能。仿真场景设置如下:传感器至于坐标原点(0,0)m,传感器量测周期=8 s。观测区域设置为[0,150 000] m×[-20 000,100 000] m,IMM和JMS的运动模型集均由一个匀速运动模型CV、一个右转模型CT(5°/s转弯速率的协同转弯模型)和一个左转模型CT(-5°/s转弯速率的协同转弯模型)组成。
CV的运动方程如下:

右转模型CT(=5π180)的运动方程如下:

左转模型CT(=-5π180)的运动方程如下:

过程噪声协方差矩阵:


马尔可夫状态转移概率矩阵给定如下:

为了一定程度上适应目标的机动,为标准δ-GLMB选取的运动模型,为辛格模型。运动方程如下:

过程噪声矩阵:



目标的存活概率设为099。目标的初始状态设置如表1所示。

表1 目标初始状态Table 1 Initial states of all targets
仿真开始后,目标1、目标2、目标3和目标5出现。其中,目标1~目标3按照CV模型运动,目标5按照CT(2 °/s左转)模型运动。在100~110 s之间,目标3转换为CT(5 °/s右转)模型运动,之后恢复为CV模型。目标4在100 s时刻出现在坐标(130 000,1 000)。在100~120 s之间,目标4按照CT(5 °/s左转)模型运动,120~140 s目标4恢复为CV模型,140~150 s之间目标4按照CT(5 °/s左转)模型运动,之后恢复为CV模型。160~200 s之间目标1和目标2按照CT(2 °/s右转)模型运动,目标3在150~250 s之间按照CT(2 °/s右转)模型运动,之后恢复CV模型运动。目标1在250 s时刻消失,至300 s时刻仿真停止。各目标运动模型转换的时序如图1所示。

图1 目标运动模型转换时序图Fig.1 Target motion model jumping sequence
目标的真实运动路径如图2所示。

图2 目标运动轨迹Fig.2 Targets’ motion trajectories
由于标准GLMB采取的已知新生目标分布的策略,无法对中断的航迹重新起始,所以本文在3种滤波器性能比较中都加入了自适应的航迹起始算法。
为了降低杂波对数据关联的影响,3种算法都采用多普勒量测信息验证关联量测点。处于跟踪波门内的多普勒量测误差过大的量测点会被滤除。多普勒信息似然度表达式为
(,+1|+1)=N(,+1;(+1),,)
(23)
式中:,+1为目标多普勒量测;,为多普勒量测方差;(+1)为多普勒观测方程。

(24)

3种滤波算法的量测方程采用极坐标形式,如下所示:

式中:dis为目标距离;为目标方位角;为传感器的轴坐标;为传感器的轴坐标。
量测协方差矩阵设置如下:

(25)

每个扫描周期的杂波点数服从均值的泊松分布,每个杂波点在观测范围内均匀分布。误差评估计算最优子模式分配(optimal sub-patten assignment, OSPA)的参数设定为=1,=1 000 m。
对δ-GLMB、JMS-GLMB和IMMG-δ-GLMB算法分别进行100次蒙特卡罗实验。探测概率取0.95,杂波率取10的情况下,航迹跟踪精度对比如图3所示。OSPA曲线的两个峰值出现位置吻合100 s时刻发生目标新生和250 s时刻发生目标消亡。

图3 3种算法跟踪精度对比Fig.3 Tracking accuracy comparison of three algorithms
为了验证不同探测概率对IMMG-δ-GLMB的影响,在杂波率取20,探测概率分别取0.95、0.85和0.75的3种情况下,进行50次蒙特卡罗实验, OSPA误差曲线如图4所示。

图4 探测概率对IMMG-δ-GLMB跟踪精度的影响Fig.4 Influence of detection probability on IMMG-δ-GLMB tracking accuracy
为了验证不同杂波率对IMMG-δ-GLMB的影响,在探测概率取0.95,杂波率分别取10、50和100的3种情况下,进行50次蒙特卡罗实验,OSPA误差曲线如图5所示。
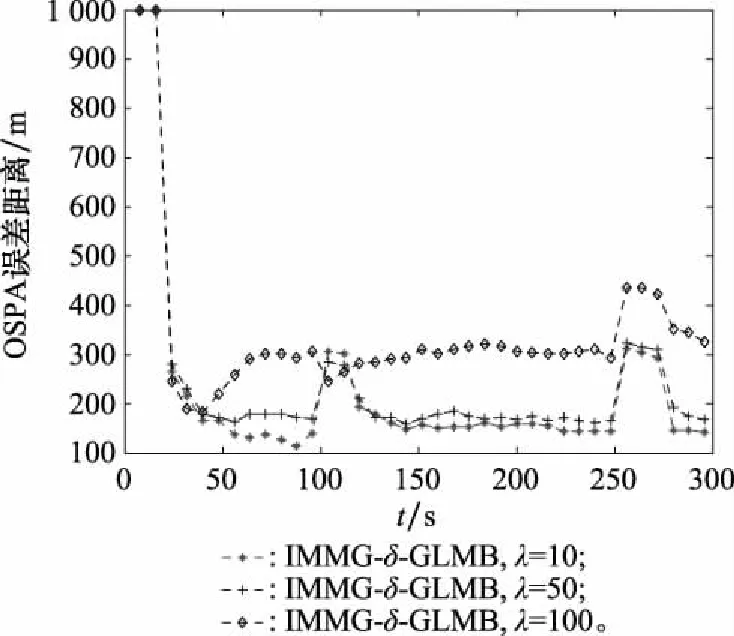
图5 不同杂波率对IMMG-δ-GLMB跟踪精度的影响Fig.5 Influence of different clutter ratios on IMMG-δ-GLMB tracking accuracy
最后,为了验证3种算法的计算复杂度随目标数量增加而增加的情况,在探测概率取0.95,杂波率取20的设定下,将场景设定的5个目标轨迹加一个随机的坐标偏移并进行复制,得到10目标、15目标和20目标场景。然后对比5目标、10目标、15目标、20目标4种情况下IMMG-δ-GLMB、JMS-GLMB和基本δ-GLMB滤波器的计算时间,结果如表2所示。

表2 3种算法不同目标数量场景的计算时间结果对比Table 2 Comparison of calculation time results of three algorithms in different target number scenarios s
实验结果分析如下。
(1) 从图3可以看出,IMMG-δ-GLMB比JMS-GLMB精度稍高,与δ-GLMB相比跟踪精度优势明显,这是因为一方面IMM与单辛格模型相比能够更好地适应目标的运动模型变化;另一方面,JMS-GLMB为了控制假设数量,在实际仿真中需要对假设数量进行的剪枝,造成误差可能超过IMM的现象,如果想要提高JMS-GLMB的精度需要保留更多的假设分支,代价是进一步提高JMS-GLMB的计算复杂度。另外,从表2可以看出,IMMG-δ-GLMB与δ-GLMB和JMS-GLMB相比计算速度更快,主要原因是IMMG-δ-GLMB采用了航迹分组计算。
(2) 从图4可以看出,IMMG-δ-GLMB的航迹跟踪精度随探测概率的下降而下降。这主要由于随着探测概率的下降,航迹需要更长时间确认起始,另外在跟踪过程中也更容易出现由于连续没有量测点导致航迹中断的问题。
(3) 从图5 可以看出,IMMG-δ-GLMB的航迹跟踪精度都随杂波率的增长而下降。但是在杂波率不高的阶段,由于采用了多普勒量测信息抑制杂波点参与航迹起始和关联,OSPA跟踪精度的下降不明显。只有在杂波率高到频繁出现虚假航迹起始和误关联时,OSPA跟踪精度才会出现比较明显的下降。
3.2 仿真场景2
为了验证传感器扫描周期、传感器探测精度、目标距离以及运动模型参数对IMMG-δ-GLMB的影响。设定一个多目标密集编队运动场景,在这个场景中由于目标之间距离较近,可以通过调整影响矩阵的参数测试航迹组数量的变化以及对应的航迹跟踪精度。
由于量测模型和状态转移模型噪声的存在,密集编队目标的航迹比较常见航迹交叉现象,为了衡量这类航迹跟踪误差,引入标签OSPA(labeled OSPA, LOSPA)误差模型,定义如下:
=+
(26)
式中:为航迹交叉次数;为单次航迹交叉引入的误差惩罚;为OSPA距离。
密集编队目标运动轨迹设定如图6所示,横纵坐标的单位均为m。5个目标间隔1 500 m编队运动,初始坐标设定为:[0707,0707,1 000]、:[0707,0707+1 500,1 000]、:[0707,0707+3 000,1 000]、:[0707,0707+4 500,1 000]、:[0707,0707+6 000,1 000],单位为m。其中为第一个目标距离传感器的距离。目标、在0 s时刻出现,、和在20 s时刻出现。

图6 密集编队目标运动轨迹Fig.6 Dense formation target trajectory
从表3选取4个参数,在不同的参数搭配下测试密集编队目标的分组情况和跟踪精度。例如参数组合[,,,]代表扫描周期1 s,方位标准差0.1°,加速度方差10 m/s,距离100 km的组合。为了消除单次实验的随机性,每组参数组合进行50次蒙特卡罗实验。

表3 影响分组的参数Table 3 Parameters affecting grouping
参数组合[,,,]情况下,分组数量曲线和LOSPA误差曲线如图7所示。LOSPA曲线出现的峰值位于目标、和的航迹起始阶段。航迹组的数量在目标、和出现之前约等于2,也就是说目标和分别处于两个航迹组内,在目标、和的航迹起始后,航迹组数量从2个增加到5个,说明目标、、、和都处于单独的航迹组内,每个航迹组内只有一条航迹。

图7 [P1,P2,P1,P3]参数对应的LOSPA误差与航迹分组数量曲线Fig.7 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P2,P1,P3]
参数组合[,,,]情况下,分组数量曲线和LOSPA误差曲线如图8所示。方位误差放大到0.2°的情况下,LOSPA略微上升和航迹组数量曲线在5个目标并存的情况下出现波动。


图8 [P1,P4,P1,P1]参数对应的LOSPA误差与 航迹分组数量曲线Fig.8 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P4,P1,P1]
参数组合[,,,]情况下,分组数量曲线和LOSPA误差曲线如图9所示,LOSPA曲线的第4和第5点较高的原因是目标、和处于航迹起始阶段。从航迹组数量可以看出目标和航迹起始阶段航迹组数量在1到2之间,目标、和航迹起始阶段航迹组数量在3到4之间,5个目标航迹全部起始完毕后,航迹组数量维持在4左右,少于目标总数5。说明出现了两个目标处于一个航迹组内的情况。

图9 [P4,P1,P1,P1]参数对应的LOSPA误差与 航迹分组数量曲线Fig.9 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P1,P1,P1]
参数组合[,,,]的情况下,分组数量曲线和LOSPA误差曲线如图10所示。由于传感器采用极坐标的原因,量测点距离目标实际位置的误差随距离的增加而增加,进而导致LOSPA误差放大,最终导致航迹数量和航迹组数量的波动。


图10 [P1,P1,P1,P4]参数对应的LOSPA误差与航迹分组数量曲线Fig.10 Curve of LOSPA error and track grouping number corresponding to parameter [P1,P1,P1,P4]
参数组合[,,,]情况下,分组数量曲线和LOSPA误差曲线如图11所示。在放大3个参数后航迹组数量保持在2,目标、合并为一个航迹组,晚20 s出现的目标、和合并为另一个航迹组。

图11 [P4,P2,P2,P1]参数对应的LOSPA误差与航迹分组数量曲线Fig.11 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P2,P1]
参数组合[,,,]情况下,分组数量和LOSPA曲线如图12所示,航迹组数量曲线已经下降到约1.5。

图12 [P4,P2,P1,P4]参数对应的LOSPA误差与航迹分组数量曲线Fig.12 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P1,P4]
参数组合[,,,]情况下,分组数量和LOSPA曲线如图13所示,航迹组数量下降到了1。

图13 [P4,P2,P3,P3]参数对应的LOSPA误差与航迹分组数量曲线Fig.13 Curve of LOSPA error and track grouping number corresponding to parameter [P4,P2,P3,P3]
从上述实验结果可以看出,高精度、高数据率以及适当的状态转移参数可以使IMMG-δ-GLMB有效地识别密集编队内的独立目标,使每个目标独立成组,此时航迹跟踪精度最高。随着探测精度和数据率的下降以及状态转移矩阵参数调整,IMMG-δ-GLMB分辨目标的能力开始下降,航迹跟踪精度也随之下降,分组数量减少,每个分组内的目标数量上升。持续放大探测误差、数据率并调整状态转移矩阵参数,航迹分组数量可以降低到1,此时IMMG-δ-GLMB的滤波迭代过程就退化为IMM-δ-GLMB。值得注意的是,调整状态转移模型参数虽然也可以改变分组情况,但是调整不当可能导致运动模型失配,严重时会造成目标跟踪失败。
4 结 论
本文在δ-GLMB的基础上引入分组滤波计算思想和IMM计算框架,利用IMM对分组处理后的JMS-GLMB进行运动模式分支合并近似,推导出IMMG-δ-GLMB的迭代方程,并给出高斯混合实现方式。
仿真结果表明,一方面,IMMG-δ-GLMB能够有效对多目标进行跟踪,与δ-GLMB和JMS-GLMB相比目标跟踪精度更高,计算速度更快。 另一方面,IMMG-δ-GLMB的分组情况受传感器精度、目标距离、扫描数据率以及状态转移参数的影响。在状态转移参数与目标运动状态匹配的情况下,高精度、高数据率的量测数据可以增加分组数量,提高算法运行效率和目标跟踪精度。反之,低精度、低数据率的情况会减少分组数量,极端情况下可能使IMMG-δ-GLMB退化为IMM-δ-GLMB。
