海上风机变径单桩基础水平承载特性数值分析

郭健，王皓，骆光杰，朱洪泽，苏凯,3,4*

(1.浙江华东工程咨询有限公司，杭州 310014；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；3.武汉大学水工岩石力学教育部重点实验室，武汉 430072；4.武汉大学海绵城市建设水系统湖北省重点实验室，武汉 430072)

随着温室效应的加剧，风能作为一种清洁能源，受到了越来越多的关注，发展风电已经成为中国可再生能源发展战略中的重要环节[1]。海上风机由于其特殊的地理位置，在服役期间常受到来自风、洋流、波浪等多种荷载的作用，对基础承载能力有较高要求。且由于海上的恶劣施工环境，海上风机投资成本远大于陆上风机，其中基础安装费用就可占总成本的15%～30%[2]。因此海上风机在基础结构的选型以及结构优化方面便有更加严格的要求。单桩基础由于结构简单且施工速度较快的优点，在海上风电场中得到了广泛应用，具有广阔开发与利用前景。一般情况下，海上风机桩基础设计主要由基础水平向承载力和变形控制，风机桩基础的水平承载性能是研究的重点[3-4]。

目前对桩体水平承载能力计算最广泛的方法为载荷-位移(p-y)曲线法，该方法通过极限地基反力法与弹性地基反力法，对桩土间相互作用进行模拟与计算。但有研究表明在大直径单桩基础计算时，p-y曲线法的结果存在较大误差[5-6]，Achmus等[7]通过对单桩基础在水平荷载作用下的模拟得出的荷载-位移曲线，对比p-y曲线法计算结果，建议在大桩径条件下尽量使用数值模拟进行计算；吴同坤等[8]通过模型试验研究了水平荷载作用下高桩基础的承载特性，并采用数值方法研究了影响高桩基础水平承载特性的主要因素；张浦阳等[9]研究了嵌岩桩基础的水平承载特性，提出了承受水平荷载下的嵌岩桩最佳嵌岩深度；潘晨晨等[10]、Templeton[11]利用ABAQUS研究了不同因素对单桩水平承载性能的影响，并开展了室内试验，证明了数值模拟的可靠性。

随着投入使用的风电装机量增大，传统的单桩形式承载性能难以满足承载要求，孔德森等[12]通过数值模拟方法研究了海上风机复合桩基础水平承载能力，对比分析了复合桩基础的承载性能优势；丁红岩等[13]通过数值模拟方法研究了单桩与导管架相结合的基础形式，可以有效提单桩的水平承载能力；但新型单桩基础结构形式复杂，施工安装难度较大，桩身变径措施较为简单，常将变径段设于海平面1 m以下，可有效减小水平荷载作用；唐娜等[14]对比了变径独立桩与通长桩的水平承载力，验证了变径措施的有效性。

然而，现有研究成果中尚未对变径桩结构的水平承载能力进行深入研究，实际设计中常依据工程经验对变径桩进行设计，也未进行系统比较。鉴于此，现基于ABAQUS建立深厚砂土地质下的变径桩模型，并研究变径桩尺寸参数对水平承载特性的影响和优化措施，希望通过研究为后续海上风机单桩基础设计提供理论指导。

1 工程背景及有限元模型建立

1.1 工程背景

参考江苏某海上风电场工程，工程布置100台单机容量4 MW风力发电机组，风机基础采用单桩基础形式。风电场海域地质属黄海滨海相沉积地貌单元，根据1985国家高程基准，海底泥面高程在-18.6～0 m。地质勘测得到风电场地基土物理力学性质如表1所示，地基持力层为⑥-3中砂土层。

表1 土层物理力学参数表

1.2 有限元数值计算模型

对变径桩模型进行适当简化，其结构示意如图1(a)所示。根据工程资料，桩顶直径DT=6.0 m，桩底直径DB=6.5 m，上部高度H1=22 m，变径段长度H2=15 m，总桩长H=84 m，桩基埋深55 m，以此钢管桩作为典型桩进行研究。

利用ABAQUS建立变径单桩基础三维有限元模型，模型采用笛卡尔坐标系，考虑边界条件影响，土体径向模型取20倍单桩底部直径长度，土层计算厚度取2倍基础埋深[15]。采用C3D8R三维8节点缩减积分六面体单元对桩体和土体进行划分，桩体网格尺寸为1 m，土体网格方面，划分密度沿径向变化，靠近桩体部分土地网格尺寸为0.75 m，网格划分后如图1(b)所示。

DT、DB分别为桩顶和桩底直径，由于桩基顶部与塔筒连接，一般情况下顶部直径不做改变；H1、H2和H分别为单桩上部长度、过渡段长度以及桩基总长度

1.3 模型设置与材料参数

地基土模型底部采用全约束，侧面采用径向约束，顶部为自由面，土体采用Mohr-Coulomb模型。钢管桩材料为Q355钢材，密度为7 850 kg/m3，弹性模量为206 GPa，泊松比为0.3。通过桩土表面属性定义面面接触，采用主-从接触算法，设置桩体为主面，土体为从面，切向采用Coulomb摩擦模型，法向采用硬接触，摩擦因数取u=tan(0.75φ)，其中φ为土体内摩擦角[16]。

采用位移加载法模拟水平荷载，通过在桩顶设置耦合点，对耦合点定义位移约束，输出耦合点反力得出单桩的荷载-位移曲线，为进行各因素承载性能比较，本文取桩顶水平位移量0.5 m。以桩顶水平位移S=0.05DB为控制标准，作为桩顶水平变形的极限状态，对应的桩顶荷载即为桩的极限水平承载力[17]。

2 计算结果分析

综合桩身水平位移与桩身弯矩分布可以判断单桩基础的水平承载能力与稳定性，因此对通长桩以及变径单桩施加0～0.5 m水平位移荷载，得到两类型单桩荷载-位移变化曲线如图2所示。并根据荷载位移对应关系获取相同水平荷载作用下两类型桩体沿桩体埋深的位移与弯矩分布，取水平荷载值为2、6、10 MN，得出桩身位移对比如图3所示，桩身弯矩对比如图4所示。根据荷载-位移曲线，可以看出通长桩与变径桩基础桩顶位移与荷载变化趋势大致相同，均为缓变型，在初始阶段基本为直线，随后曲线斜率逐渐减小，无明显转折点。

图2 通长桩与变径桩荷载-位移曲线

这是由于在初始变形阶段桩周土体发生弹性变形，随着荷载增加，部分桩周土体发生塑性变形，随变形产生的反力增量逐渐减小。变径桩荷载-位移曲线斜率整体大于通长桩，在两类型桩基桩顶受到0.5 m位移荷载时，变径桩桩顶反力较通长桩增加了1.2 MN，约增加12%。从图3可以看出，变径桩基础桩身位移变化趋势与通长桩基础大体相似，均在桩高约26 m(埋深29 m)处出现正向位移，在桩顶处，两类型桩基位移差别最大。详细位移差别如表2所示，可以看出相对于通长桩，变径单桩基础在同级荷载作用下位移均有较为明显减小，减小率为11%左右，因此，采用桩身变径措施，能有效减小单桩受水平荷载作用下的桩身位移，且减小比例自泥面到桩顶处基本保持一致。

表2 分级荷载下变径桩与通长桩位移对比

图3 通长桩与变径桩桩身位移曲线

由图4可知，变径桩与通长桩在受水平荷载作用下，其桩身弯矩分布与变化规律大致相同，最大弯矩均出现在桩高约47 m(埋深8 m)处。在2 MN水平荷载作用下，相较于通长桩，变径桩桩身最大弯矩减小量约为5.6 MN·m，减小率约为8.07%，此后再随着水平荷载增大，桩身弯矩最大值无明显变化。采用变径措施不改变桩身弯矩分布情况，但可小幅度减小桩身弯矩幅值。

图4 通长桩与变径桩桩身弯矩分布曲线

总体而言，采用桩身变径措施可以有效减小桩身位移与提高基础承载能力，相较于通长桩，变径桩具有更好的水平承载能力。

3 水平承载特性影响因素分析

3.1 底部桩径影响

为研究桩径与壁厚对桩体水平承载力的影响，在保证变径段位位置、长度以及整体用钢量相同的条件下，采用以下不同桩径与壁厚的单桩基础进行计算，参数如表3所示。其中3号桩为参考典型桩型。

表3 不同桩径的桩体尺寸

图5为桩号1、3、5、7的单桩，在桩顶施加相同水平位移荷载下的基础荷载-位移曲线，可以看出，在6.0～7.5 m桩径范围内，桩的承载性能是递增的。由图6可知，变径桩的水平承载力随底部桩径的增大而逐渐增大，基本呈线性增长的趋势。对比6 m桩径的通长桩，7.5 m底部桩径的变径桩水平极限承载力了约53%。桩径增大能够显著提高变径桩的水平承载能力。

图5 不同底部桩径下单桩荷载-位移曲线

图6 单桩极限水平承载力随桩径的变化曲线

根据荷载位移对应关系获取相同水平荷载作用下两类型桩体沿桩体埋深的位移分布，取水平荷载值为10 MN，得出在同级荷载下桩身位移对比如图7所示，可以看出，随着底部桩径增大，桩身整体位移均有所减小，其关键部位位移变化如图8所示，随底部桩径增大，桩顶位移逐渐减小，其位移值逐渐趋向一稳定值；泥面处位移整体来看逐渐减小，但在较小直径范围内，增大底部直径，泥面处位移有所增大。因此在变径单桩的实际设计中，仍需要结合壁厚以及桩身位移等因素综合确定合适的桩径大小。

图7 不同底部桩径下桩身位移曲线图

图8 不同底部桩径下桩身关键部位位移变化曲线

3.2 变径段埋深影响

以3号桩为基础，仅改变变径段埋深，使得变径段完全脱出泥面至没入泥面，各变径段埋深方案如表4所示。

表4 不同变径段埋深的桩体尺寸

其数值计算结果如下，图9为不同变径段埋深下桩体荷载-位移曲线，可以看出桩基在水平荷载下的位移变化规律无明显变化，表明变径段高度变化对桩土变化规律没有影响。图10为桩体极限水平承载力随变径段埋深高度变化情况，随着变径段埋深增加单桩水平承载力逐渐降低，相比于0 m埋深，15 m埋深下水平承载力降低约0.40 MN，降低率约为5%。这是由于变径段位置在桩体中整体下移减小了单桩整体刚度，并且下部大直径桩段长度降低，也会减弱砂土对桩体的嵌固效果。在7.5～10 m的埋深内，水平承载力未有明显降低，在其他埋深范围内，水平承载力基本呈线性变化。

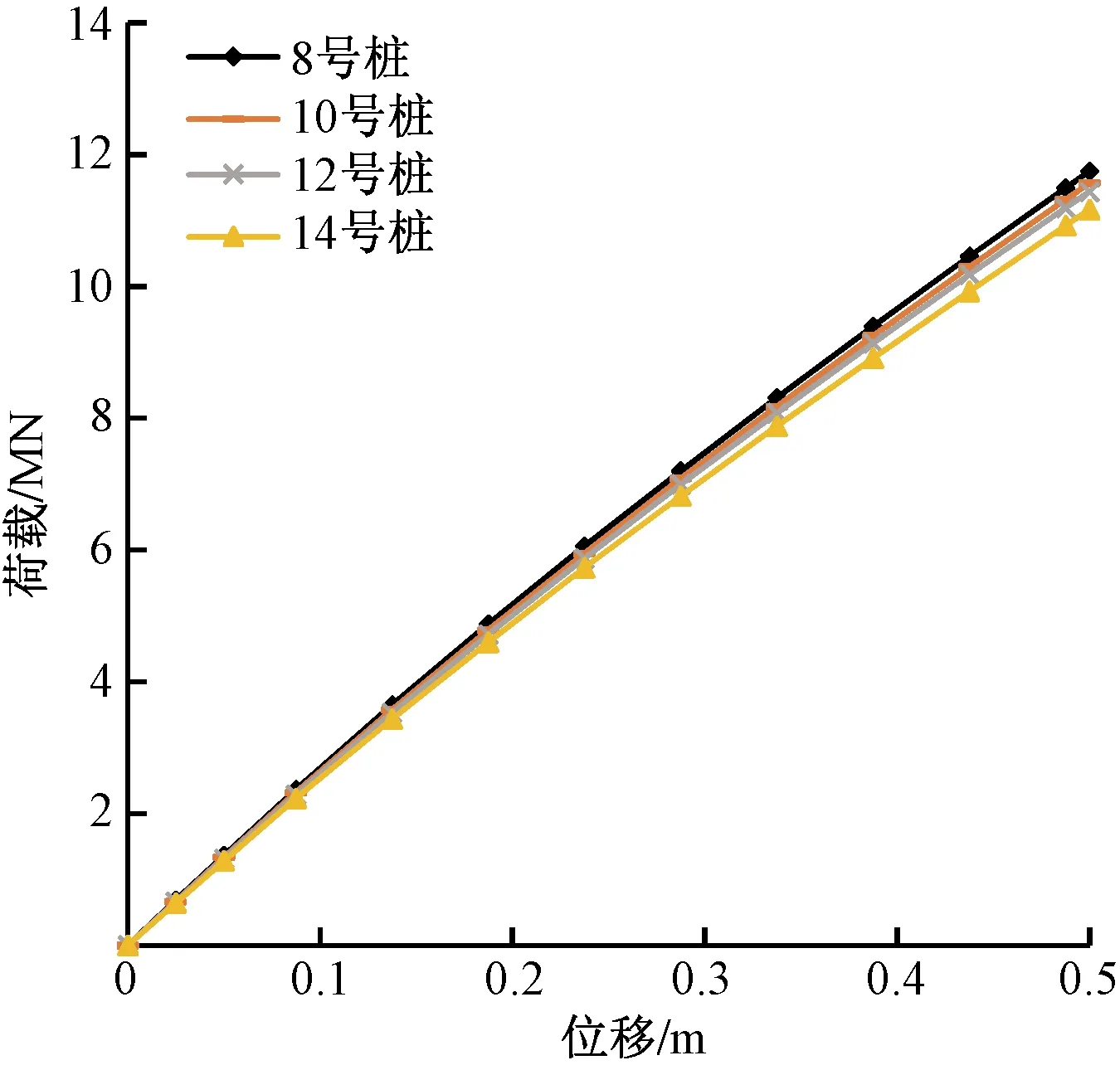
图9 不同变径段埋深下的荷载-位移曲线

图10 单桩极限水平承载力随变径段埋深的变化曲线

除研究桩基承载力大小变化规律，也应对桩身泥面及以下位移进行考虑，由于各桩号下桩体位移变化规律基本一致，因此仅对在桩顶施加0.5 m位移荷载作用下，变径段埋深高度为0 m与15 m的桩身泥面下变形分布如图11所示，其变化规律基基本没有改变，且随着变径段埋深增大，桩身泥面处位移有所减小，相对比零埋深，15 m埋深下泥面处位移减小了约21.0 mm，减小率约为12.47%。因此，对于变径单桩变径段埋深高度选取，应综合桩体水平承载力、用钢量以及泥面下桩身位移等因素进行确定。

图11 桩体水平位移曲线

3.3 变径段长度影响

以桩号3为基准，保持其他条件不变，改变变径段长度，其具体尺寸参数与编号如表5所示。

表5 不同变径段长度的桩体尺寸

计算得到不同变径段长度变径单桩基础的水平极限承载力与泥面下桩身位移分布，如图12、图13所示。在相同桩顶位移条件下，随着变径段长度增大，变径单桩极限水平承载能力小幅度减小。其中变径段长度为25 m下的单桩水平承载能力最小，为7.39 MN，相较于变径段为5 m的单桩仅减少约0.05 MN；泥面下桩身位移方面，其分布与变化规律未发生改变，对比5 m与25 m变径段长度下泥面桩身位移，变径段25 m的变径桩泥面位移增大约0.82 mm。可以看出改变变径段长度对单桩水平承载力及桩身变形几乎没有影响，对比计算结果可知：增大变径段长度对桩身承载力的提升十分有限。

图12 单桩极限水平承载力随变径段长度的变化曲线

图13 桩体水平位移曲线

4 结论

通过数值模拟方法，对比分析了海上风机变径单桩基础相较于通长桩基础的承载力优势，并进一步分析了变径桩变径段尺寸参数对变径桩基础承载能力的影响，得出如下主要结论。

(1)在相同水平位移荷载作用下，变径桩桩顶水平反力明显大于通长桩，其水平极限承载力也大于通长桩；在相同水平荷载作用下，相较于通长桩，变径桩基础桩身位移有较为显著的减小，最大弯矩方面有较小幅度减小。总体而言变径桩基础具有更好的承载能力与稳定性。

(2)变径段直径改变对桩基承载能力有较大影响。随着底部桩径的增大，单桩基础的水平极限承载力逐渐增大，其增大趋势基本呈线性；在相同荷载作用下桩身关键位移随桩径增大有明显减小，但随桩径变化幅度逐渐减小。

(3)变径段埋深改变也对桩基承载能力有较为明显的影响。随着埋深增大，桩身泥面处及以下位移有所减小，桩基极限水平承载力逐渐减小。

(4)变径段长度对于变径桩承载能力影响较小。随着变径段长度增加，变径桩水平承载力逐渐减小，桩身泥面及以下位移逐渐增大，但其变化趋势较小，改变变径桩长度对桩身承载能力提升与优化作用有限。